在役鋼筋混凝土梁橋極限承載力簡化分析方法

張世春，朱勁松,2

（1.天津大學 建筑工程學院，天津 300072；2.天津大學 濱海土木工程結構與安全教育部重點實驗室，天津 300072）

在役鋼筋混凝土梁橋極限承載力簡化分析方法

張世春1，朱勁松1,2

（1.天津大學 建筑工程學院，天津 300072；2.天津大學 濱海土木工程結構與安全教育部重點實驗室，天津 300072）

針對目前應用較為廣泛的鋼筋混凝土梁橋，提出了基于混凝土梁單元-剛臂元-彈簧單元-鋼筋單元體系的ANSYS有限元非線性分析模型．并以量大面廣的鋼筋混凝土簡支T型梁橋為例，利用該有限元非線性分析模型對影響其極限承載力的各個參數進行了分析研究，以此推導出了此類簡支梁橋的極限承載力公式．最后通過一些實橋分析，對比ANSYS與推導公式的計算結果，驗證了該公式的可靠性．

鋼筋混凝土；T型梁橋；極限承載力；非線性分析；公式推導

0 引言

鋼筋混凝土橋梁是當今世界應用最為廣泛的橋梁結構之一．長期使用以來，人們逐漸意識到鋼筋混凝土橋梁存在著嚴重的承載力退化問題．而我國大部分橋梁建于上個世紀80年代以前，由于材料的長期退化，目前承載力已明顯下降，危橋逐漸增多．及時對此類橋梁進行承載力評估已成為一項刻不容緩的工作，必須積極開展相關的研究并付諸實踐．在承載力評估當中，橋梁結構的極限承載力評估較之設計承載力而言，往往更具有現實意義．這是因為結構設計計算針對的是單個構件，且采用的是簡化的理想彈性力學模型，這都與實際橋梁的受力行為有所不同．而以結構為對象的極限承載力，只能是以結構完全喪失剛度為標志[1]．

目前，國內外已有不少學者針對在役混凝土橋梁極限承載力問題進行了相關研究，主要采用非線性有限元分析模型．Andrea Dall'Asta等[2]基于有限變形理論推導出小應變和中等轉動理論，提出了一個完整考慮幾何和材料非線性的分析模型；AshrafAyoub[3]采用梁單元、鋼束單元和連接單元，提出了一種考慮粘結滑移、摩擦力和錨固損失的非線性有限元模型；HelderSousa等[4]則在非線性分析中考慮了混凝土強度和彈性模量隨時間的變化；朱勁松等[5]針對鋼筋混凝土梁橋，提出了基于平面應力單元-彈簧單元-桁架單元體系的二維有限元非線性分析模型；葉見曙等[6]針對預應力混凝土多T梁橋，基于實體退化殼單元理論，考慮材料非線性效應，研究了多T梁橋極限承載力的計算方法；吳光宇等[1]針對大跨預應力混凝土橋梁極限承載力的計算問題，提出了建立在三維實體退化虛擬層合單元理論基礎上同時考慮結構雙非線性的空間分析計算方法．國內外雖然已在在役混凝土橋梁極限承載力方面做了不少研究，但均需要通過有限元非線性分析來獲得橋梁的極限承載力，這種方法較為復雜，適用人群較為局限而不易廣泛應用．

本文旨在尋找求解極限承載力的簡便方法，以目前量大面廣的鋼筋混凝土簡支T型梁橋為例，利用有限元非線性分析模型對影響其極限承載力的參數進行分析研究，找出極限承載力與其截面尺寸、配筋情況以及跨徑等的關系，從而推導出鋼筋混凝土簡支T型梁橋的極限承載力快速計算公式，并通過實橋算例驗證了本文所提公式的可靠性．

1 材料本構模型

1.1 混凝土本構模型

隨著齡期增長，混凝土與酸性氣體發生反應而造成碳化．混凝土碳化后，其抗壓強度有所增加，但總體而言，對抗彎承載力的影響不大[7]，故而不考慮混凝土抗壓強度的變化．混凝土本構關系上升段采用GB50010-2002模型，下降段采用Hongnestad模型[8]：

1.2 銹蝕鋼筋本構模型

鋼筋銹蝕是導致橋梁承載力降低的主要因素之一．鋼筋銹蝕后，其屈服強度有所減小，但鋼筋彈性模量基本不變[9]，考慮銹蝕影響對鋼筋理想彈塑性本構關系做如下修正：

1.3 銹蝕鋼筋/混凝土粘結滑移模型

鋼筋與混凝土之間擁有足夠的粘結強度是兩者得以共同工作的基礎，但由于鋼筋銹蝕，使得鋼筋與混凝土之間的粘結強度顯著降低，導致鋼筋在較小的應力下便能產生較大的滑移量，因而對其影響應予以考慮．為此，徐善華等[10]提出了粘結強度銹蝕影響系數，得出銹蝕鋼筋粘結滑移公式：

圖1 混凝土應力-應變曲線Fig.1 Stress-strain constitutive curveof concrete

圖2 鋼筋應力-應變曲線Fig.2 Stress-strain constitutive curveof rebar

式中： 為粘結強度，MPa；0為未銹蝕鋼筋的粘結強度，MPa，按下式計算：

式中：s為滑移距離（mm）；ft,s為混凝土劈裂抗拉強度（MPa）；c為混凝土保護層厚度（mm）；d為鋼筋直徑（mm）．其粘結滑移曲線如圖3所示．

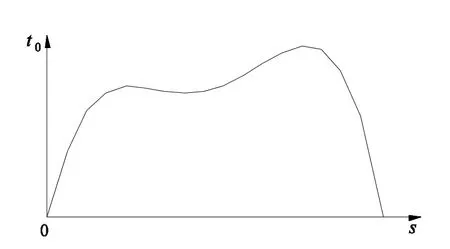
圖3 未銹蝕鋼筋/混凝土粘結滑移曲線Fig.3 Curveof bond and slip between rebar w ithoutcorrosion and concrete

式 (3)中， 為粘結強度銹蝕影響系數，按下式計算：

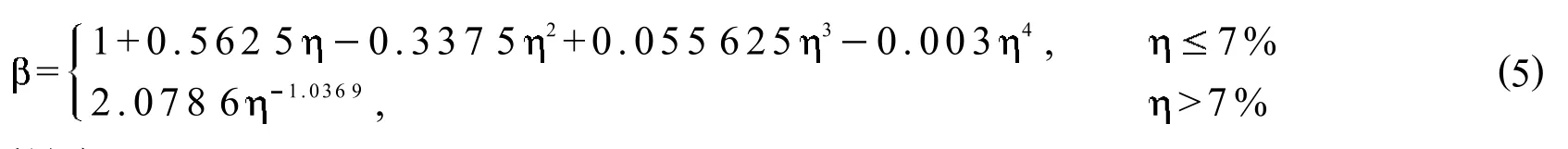
2 有限元建模方法

采用通用有限元軟件ANSYS建立結構有限元模型，進而對結構進行整體非線性分析．一般而言，三維實體模型的計算結果相對精確，但其計算量也相對較大，因而更適用于局部分析．對于鋼筋混凝土梁橋的整體非線性分析，采用基于梁單元-剛臂元-彈簧單元-鋼筋單元體系的空間梁格模型，如圖4所示．

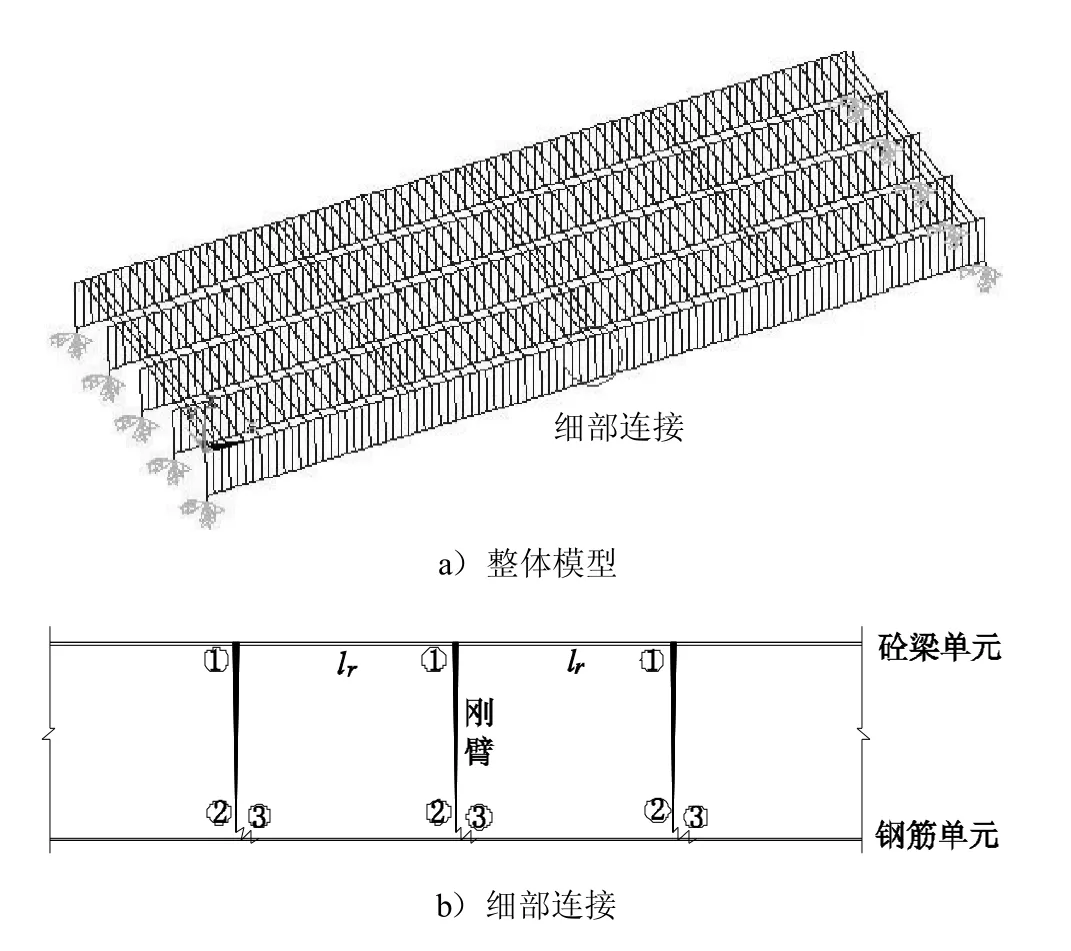
圖4 非線性有限元模型Fig.4 Nonliner finiteelementmodel

混凝土梁采用3D梁單元beam189模擬，考慮剪切變形影響，其本構關系采用多線性隨動強化模型 KINH；縱梁之間采用虛梁連接，即不考慮虛梁自重，對于T型梁橋，虛梁梁高取翼板邊緣厚度；鋼筋采用3D桿單元link8模擬，通過改變單元截面和強度條件來模擬不同銹蝕情況下的鋼筋截面面積和鋼筋強度，其本構關系采用雙線性隨動強化模型BKIN．

在支座處建立支座節點，與對應梁節點之間采用剛臂連接，剛臂采用3D梁單元beam4模擬，其彈性模量E取1000Ec；混凝土梁與鋼筋之間的連接如圖4所示，節點①為混凝土梁單元上一點，節點②與鋼筋節點③重合，節點①、②之間采用剛臂連接，節點②、③之間采用非線性彈簧單元連接，以模擬鋼筋/混凝土粘結滑移，其沿鋼筋縱向的荷載-位移關系如下式所示：

式中：F為粘結力（N）；n為同一高度處的鋼筋數量；dc為銹蝕鋼筋有效直徑（mm）；lr為彈簧單元沿鋼筋縱向的間距（mm）； 為式(3)中的粘結強度（MPa）．

3 極限承載力簡化分析方法

3.1 基準模型

以某鋼筋混凝土梁橋T梁截面尺寸為基準，見圖5，布置兩層受拉鋼筋和一層受壓鋼筋，鋼筋直徑取20 mm，鋼筋屈服強度取275 MPa，并采用C20混凝土，以此建立有限元基準模型，如圖4所示．在此基礎上，分別研究跨徑l、梁高h、腹板寬b、翼緣板寬bf、翼緣板厚hf、受拉主筋面積As、受壓主筋面積A's、混凝土抗壓強度fck、鋼筋屈服強度fyk、受拉主筋中心距as、受壓主筋中心距a's、受拉主筋平均銹蝕率、受壓主筋平均銹蝕率'、主梁數n以及車道數m對其極限承載力qu的影響．此處極限承載力qu為全載作用下單個車道所加載的最大均布荷載．

3.2 公式推導

3.2.1 參數分析

逐一改變各個參數數值，采用ANSYS進行有限元非線性分析，計算各參數值對應的極限承載力，并首先分析出單梁極限承載力q1u與各參數的對應關系，然后考慮主梁數n與車道數m對極限承載力qu的影響，從而進一步推導出極限承載力公式．目前，國內的鋼筋混凝土簡支T型梁橋跨徑一般為8～20m；對應梁高一般為0.8～1.3 m；主梁間距一般為1.5～2.2 m；腹板厚度一般為160～240mm；翼板邊緣厚度不小于80mm；橫隔板一般設置于主梁1/2、1/4及支座處，高度約為梁高的3/4，寬度一般為120～200mm．各參數數值變動即以此為參照，單梁極限承載力q1u計算結果見圖6．

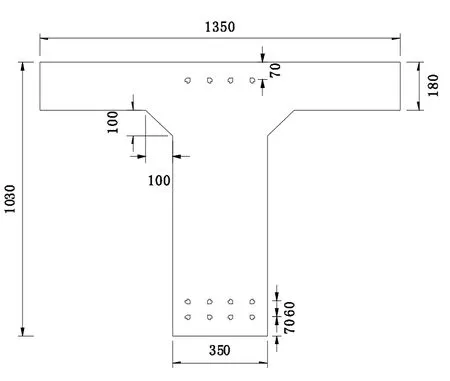
圖5 基準T梁截面圖（mm）Fig.5 Section diagram of reference T beam

3.2.2 單梁極限承載力

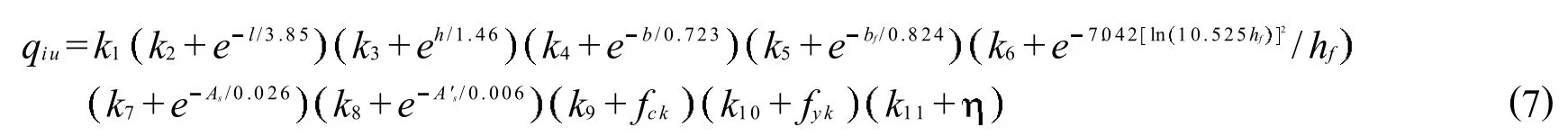
則單梁極限承載力與各參數的對應關系式可視為式 (7)的特殊情況，即若以參數l為變量，其余參數均按基準截面數據取為定值，則所得公式q1u=C k2+el/3.85應與公式q1u=24.996+1928.946el/3.85相同，據此可得k2，同理可求得k3～k11，在求得k2～k11后，可通過代入特殊值求解k1，具體求解結果見表1．

表1 系數k1～k11計算結果Tab.1 Calculation resultsof coefficient k1～k11

3.2.3 多梁極限承載力

前面推導出的僅僅是單梁極限承載力，而現實中的簡支T型梁橋沿橫向有多根主梁，因而需進一步研究多梁橋極限承載力qu與單梁極限承載力q1u之間的關系．此外，絕大多數的梁橋擁有兩個車道或以上，車道數不同則荷載布置數量也不同（幾個車道即施加幾道均布荷載），故而也需對車道數的影響進行分析．本文以基準T梁截面的8 m跨徑簡支梁為例，對比分析了車道數為1、2、3時1、3、5、7、9片梁對應的極限承載力，具體計算結果見表2．

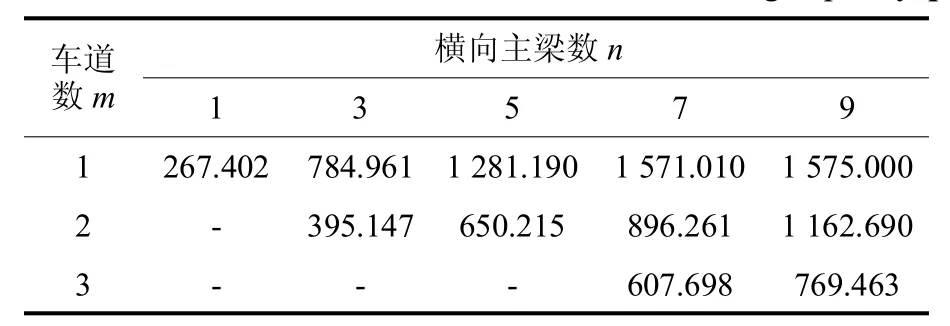
表2 極限承載力qu計算結果 kN/mTab.2 Calculation resultsof ultimate load bearing capacity qu

橫向觀察表2可以看出，當車道數為1時，1、3、5片梁對應的極限承載力比值為1∶2.936∶4.791，極限承載力qu與主梁數n近似呈正比例關系；當主梁數超過5片時，此時橋寬大于橋長，正比例關系不再成立，且7、9片梁對應的極限承載力幾乎相同，即9片梁的最外側兩根梁幾乎不受影響．說明一道均布荷載的影響范圍有限，越往外側影響越小，而當橋寬小于橋長時，每根梁均能得到充分利用，因而其極限承載力qu與主梁數n呈正比例關系．當車道數為2時，3、5、7、9片梁對應的極限承載力比值為3∶4.937∶6.805∶8.827，當車道數為3時，7、9片梁對應的極限承載力比值為7∶8.863，其極限承載力qu與主梁數n均近似呈正比例關系，原因在于此時橋寬小于2倍橋長，兩道均布荷載即可使每根梁得到充分利用．

豎向觀察表2不難發現，3、5片梁對應的極限承載力qu與車道數m近似成反比；車道數大于1時，7、9片梁對應的極限承載力qu亦與車道數m近似成反比，原因與上述相同，均取決于主梁是否得到充分利用．

根據上述分析，可以假設：

式中：f n為單車道下n梁極限承載力與單梁極限承載力的比值；g m 為單車道對應極限承載力與m車道

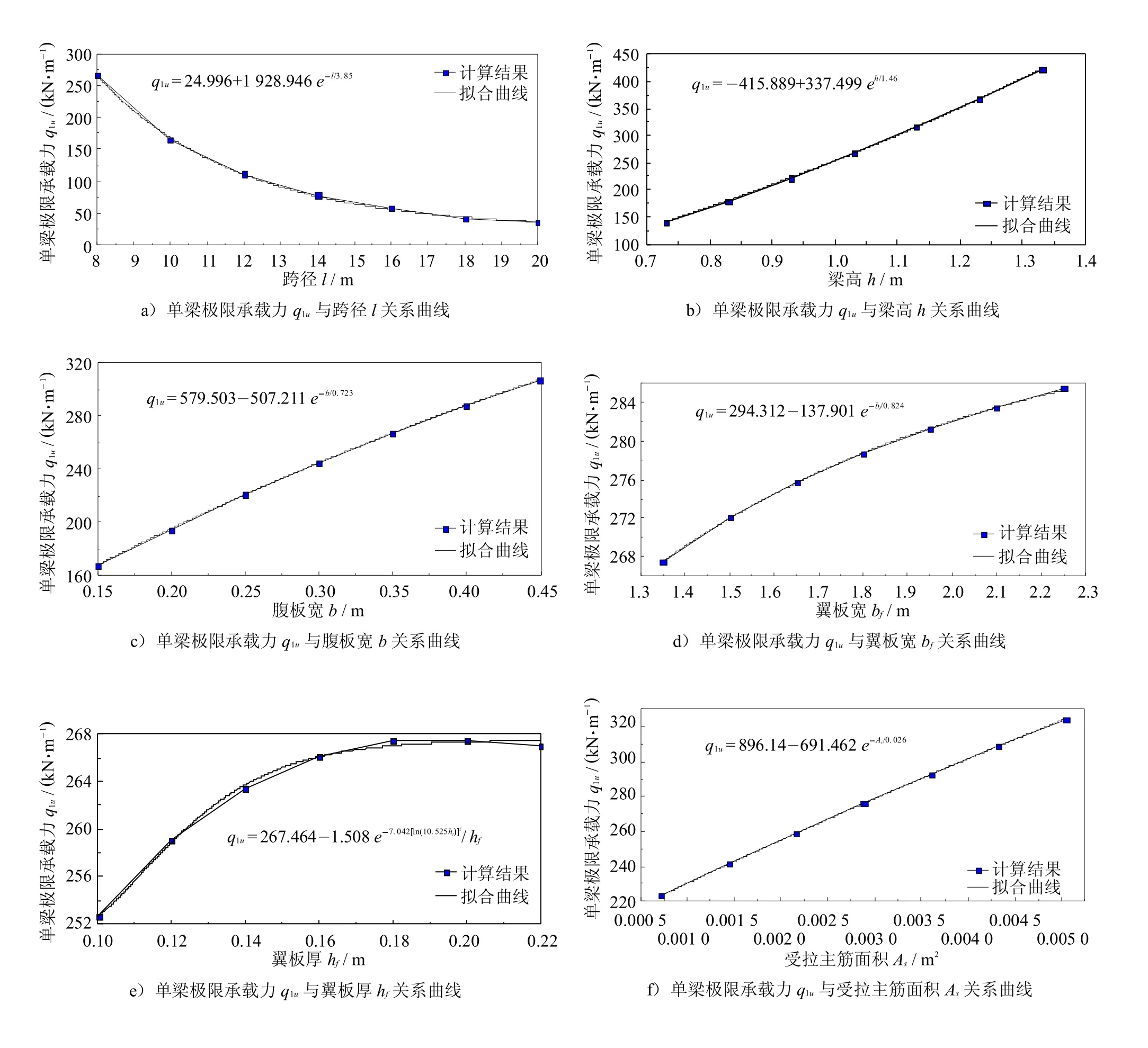
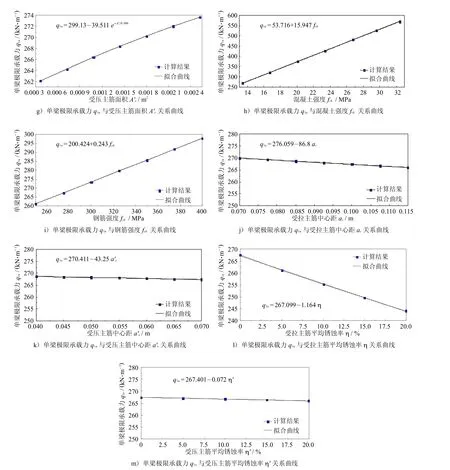
圖6 單梁極限承載力q1u曲線圖Fig.6 Curve chartof ultimate load bearing capacity q1uof singlebeam

對應極限承載力的比值，且f n與n、g m 與m均呈線性關系．

當車道數m為1時，根據表2中1、3、5片梁對應的數據求解f n，f n與n的具體關系見表3、圖7．

f n與n的擬合曲線公式 (9)

根據表2中3、5片梁對應的數據亦可求解g m ，g m 與m的具體關系見表4．

表3 關系表Tab.3 Relationship betweenand n

表3 關系表Tab.3 Relationship betweenand n

n 1 3 5 f n 1 2 . 9 3 6 4 . 7 9 1

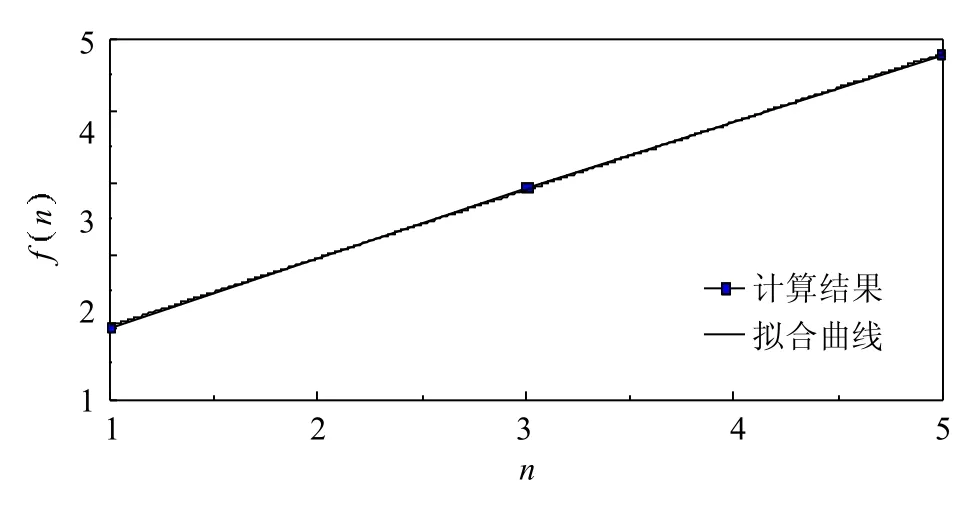
圖7 f n與n的關系曲線Fig.7 Curveof relationship between f n and n

根據表4可以求得：

其中

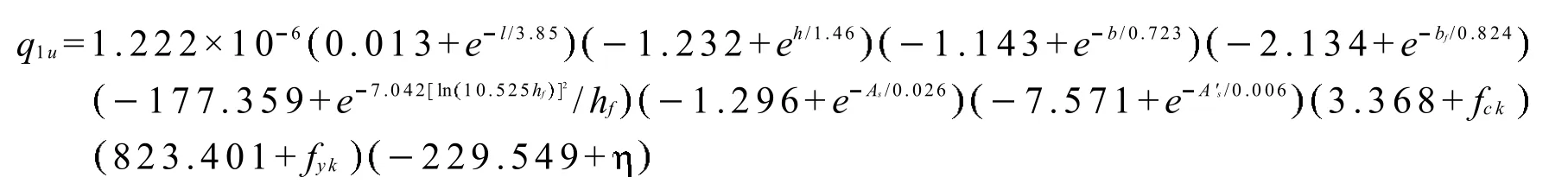
式中：l為跨徑（m）；h為梁高（m）；b為腹板寬（m）；bf為翼緣板寬（m），取主梁橫向間距；hf為翼緣板平均厚度（m）；As為受拉主筋初始面積（m2）；A's為受壓主筋初始面積（m2）；fck為混凝土軸心抗壓強度標準值（MPa）；fyk為鋼筋初始屈服強度標準值（MPa）；為受拉主筋平均銹蝕率（%）．

表4 g-m關系表Tab.4 Relationship between gand m

表4 g-m關系表Tab.4 Relationship between gand m

m 1 2 g m 梁數n 3 1均值 梁數n 3 1 . 9 8 7 均值5 1 1 5 1 . 9 7 0 1 . 9 7 8

根據模型及分析可知，該公式僅當主梁翼板剛接且每片主梁均得到充分利用時適用，即：橋寬小于橋長時，適用于任何車道數；橋寬大于橋長而小于2倍橋長時，適用于兩車道及以上．但對于實際簡支梁橋，當橋寬大于橋長時，一般均有多條車道，因而該公式普遍適用于翼板剛接的鋼筋混凝土簡支T型梁橋．

3.3 分析驗證

為了驗證鋼筋混凝土簡支T型梁橋極限承載力快速計算公式的正確性，本文選取了一些實際簡支T型梁橋，并假定鋼筋銹蝕率均為0，采用ANSYS對其進行有限元非線性分析，計算各自極限承載力，并與公式計算結果進行對比．實橋截面尺寸、配筋情況等信息及對比驗證結果見表5．

由表5可見，公式 (11)計算所得極限承載力與ANSYS分析計算所得極限承載力基本一致，除橋6、8誤差達到 8%外，其余誤差均在 5%以內，因而可以認為本文所推導的鋼筋混凝土簡支T型梁橋極限承載力快速計算公式在理論上正確可靠，可為在役鋼筋混凝土簡支T型梁橋極限承載力快速評估提供參考．

4 結論

本文旨在分析在役鋼筋混凝土梁橋的極限承載力，并針對目前應用較為普遍的鋼筋混凝土簡支T型梁橋，以基于混凝土梁單元-剛臂元-彈簧單元-鋼筋單元體系的ANSYS有限元非線性分析模型為計算手段，對影響鋼筋混凝土簡支T型梁橋極限承載力的各個參數進行了分析研究，以此推導出其極限承載力快速計算公式．并通過一些實橋分析，對比ANSYS與推導公式的計算結果，驗證了該公式的可靠性．

具體結論如下：1）本文所推導公式可作為在役鋼筋混凝土簡支T型梁橋極限承載力的評估依據，且該公式計算較為方便，從而為此類橋梁的極限承載力評估提供了便利；2）單梁極限承載力與各參數基本呈非線性關系，且當各片主梁得到充分利用時，多梁極限承載力與主梁數呈正比；3）本文極限承載力快速計算公式的推導方法具有一定的可借鑒性，可根據該方法對其它類型梁橋的極限承載力進行研究．

表5 實橋極限承載力驗證結果Tab.5 Test resultsofultimatebearing capacity of realbridge

[1]吳光宇，楊升善，汪勁豐，等．大跨預應力混凝土橋梁極限承載力計算 [J]．南昌大學學報（理科版），2013，37（2）：198-204．

[2]AndreaDall'Asta，LauraRagni，A lessandro Zona．AnalyticalModel forGeometricandMaterialNonlinearAnalysisofExternally Prestressed Beams [J]．JEng Mech，2007，133：117-121．

[3]Ashraf Ayoub．Nonlinear Finite-ElementAnalysisof Posttensioned Concrete BridgeGirders[J]．JBridge Eng，2011，16：479-489．

[4]HelderSousa，Jo?o Bento，Joaquim Figueiras．Constructionassessmentand long-term predictionofprestressed concretebridgesbasedonmonitoring data[J]．Engineering Structure，2013，52：26-37．

[5]Zhu Jinsong，Gao Change．Probabilistic durability assessmentapproach of deteriorating RC bridges[J]．Journal of Southeast University(English Edition)，2011，27（1）：70-76．

[6]葉見曙，張劍，黃劍峰．預應力混凝土多T梁橋的極限承載力 [J]．東南大學學報（自然科學版），2009，39（1）：106-111．

[7]馬廣強．腐蝕與疲勞耦合作用下鋼筋混凝土橋梁數值模擬方法研究 [D]．天津：天津大學，2010．

[8]王新敏．ANSYS工程結構數值分析 [M]．北京：人民交通出版社，2007．

[9]張偉平，商登峰，顧祥林．銹蝕鋼筋應力-應變關系研究 [J]．同濟大學學報，2006，34（5）：586-592．

[10]徐善華．混凝土結構退化模型與耐久性評估 [D]．西安：西安建筑科技大學，2003．

[責任編輯 楊 屹]

Simplified analysismethod forultimatebearing capacity ofexisting reinforced concrete girderbridges

ZHANG Shichun1，ZHU Jinsong1,2

(1.SchoolofCivilEngineering,Tianjin University,Tianjin300072,China;2.Key Laboratory ofCoastCivilStructureSafety(Tianjin University),M inistry of Education,Tianjin 300072,China)

For thew idely used reinforced concretegirderbridges,thispaperproposesan ANSYS finiteelementnonlinear analysismodelbased on the system of concretebeam element-rigid arm element-spring element-reinforced element.And taking thew idespread reinforced-concrete-simply supported-T beam bridge as an example,this paperanalyses the parameters thataffect its ultimate bearing capacity w ith this finite elementnonlinear analysismodel to derive the formula of ultimate bearing capacity of such bridges.Finally,the reliability of the formula is verified through the analysis of some realbridgesand comparing the calculation resultsof ANSYSand the formula.

reinforced concrete;T-beam bridge;ultimate bearing capacity;nonlinearanalysis;formula derivation

TP183；U448

A

1007-2373(2016)02-0096-08

10.14081/j.cnki.hgdxb.2016.02.017

2015-07-20

國家自然科學基金（51178305）；天津市應用基礎與前沿技術研究計劃（14JCYBJC21500）

張世春（1991-），男（漢族），碩士生．通訊作者：朱勁松（1975-），男（漢族），教授，博士，博士生導師．