基于抽象性的函數問題分類
王 康
(呂梁學院汾陽師范分校,山西 汾陽032200)
?
基于抽象性的函數問題分類
王 康
(呂梁學院汾陽師范分校,山西 汾陽032200)
通過對函數抽象性表征的分析,從人們認識事物對象時思維方式的轉變過程這一角度,文章將函數問題進行分類,以期找到有效解決函數抽象性問題的解決策略。
函數;抽象性;思維方式
高一學生學習的函數概念是第二次接觸了,是站在了一個新的高度,變換了一個認識的角度,再次學習函數概念,主要體現在知識內容的廣度上陡然增大,學習內容的深度上越來越抽象。相比于初中學習的函數來說,高一學習的函數增添了許多新內容,比如定義域、值域、對應法則、函數性質及符號化、形式化的表述等等,而這些新內容是看不見、摸不著的,似乎感覺沒有什么實用性,充分體現出學生認知結構的不完整。
高一學生所面臨的抽象問題分為相對的抽象和絕對的抽象。相對的抽象主要來自于函數概念的抽象性表征,比如函數本質屬性的認識、函數基本性質的理解等,屬于認知層次的抽象;絕對的抽象是指對函數問題符號化、形式化表述的深刻認識和沒有解析式的純抽象函數問題,主要體現在學生邏輯推理能力和思維的深刻性,屬于思維層次的抽象。文章從函數的各種抽象性表征出發,結合教學實際,將函數問題進行分類。
1 函數的抽象性表征
表征即信息在頭腦中的呈現方式,從長期的教學實踐和前人的研究成果來看,對于學生來說,函數的抽象性表征主要表現在如下幾個方面:
1.1 符號化、形式化的抽象表征
數學符號是在數學抽象化的基礎之上由數學家們在研究工作中逐步引入的,而數學符號的逐步引入,又促進了數學的形式化,只有形式化,才能揭示數學對象的基本結構和基本特征,保證數學推理和演算的嚴密性,促進數學科學的繁榮與進步[1]。但是,數學抽象符號的使用在提高運算、證明速度的同時,也增加了其本身承載的信息量,使得學生在數學學習和數學解題中遇到了很多來自數學符號的困惑,致使一些學生感覺讀不懂題,無從下手。

數學抽象符號的正確認識是進一步形式化表述、書寫的前提,學生如果對其沒有正確的認識,就不能從變量對應的角度理解函數,當其獨立解題時只能靠死記硬背,生搬硬套,而這種機械記憶、模仿重現的學習方法對人的大腦皮層刺激方法單一,很容易產生遺忘,到頭來還是不會做題.從而直接導致很多方法(待定系數法、換元法、賦值法、配湊法等)是一知半解,不能領會到方法的本質,普遍出現“聽而不懂”、“懂卻不會”、“會卻做不對習題”的怪現象。
1.2 圖像與性質的抽象表征
函數圖像的幾何特征與習題中的數量特征緊密結合,是數形結合解決函數問題的根本之所在,圖像的抽象表征是一種站在方法論的角度處理函數抽象性問題的有力工具。然而,學生在實際解題時常常表現出來的是,畫不出圖與讀不懂圖。
函數的基本性質是刻畫函數圖形特征的,是較函數概念更高層次的抽象,因為其中夾雜了自變量之間、函數值之間的關系比較,具體的抽象表征體現在:第一,概念敘述抽象,其中加入了簡易邏輯中的全稱量詞“任意”二字,在實際教學中,初學的同學經常會把“任意”二字特殊化;第二,性質的應用,在綜合性的題目當中,函數的基本性質發揮了極其重要的樞紐式的作用,所以要理解函數性質抽象表征背后的實質,如單調性是為了刻畫函數變量間的不等關系,奇偶性是為了刻畫函數圖形的對稱特征。
1.3 函數屬性的抽象表征
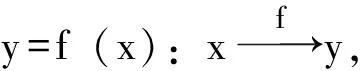

2 基于抽象性的函數問題分類
抽象和具體是人們認識客觀對象的完整的思維方式,人們認識事物對象時,首先是通過感覺、知覺所把握的各種感性規定性的綜合,反映的是具體的事物對象,我們把它稱之為感性具體。在這一基礎上,人們使用分析的方法,從眾多具體事物對象中舍棄個別的、非本質的東西,抽象出共同的本質屬性,這樣,人們的認識就從感性具體發展成理性抽象,更進一步,弄清抽象對象各部分間的內在聯系,每一個規定占什么地位,起什么作用,把各種抽象的規定進行更深刻的思維加工,再從總體上把握某一具體事物對象,使人們對具體事物對象的認識又由理性的抽象上升到理性的具體或者思維的具體。正是借助于抽象和具體的方法,人們對客觀事物的認識不斷的有現象向本質深入、由片面向全面發展,我們把人們認識客觀對象的一般思維方式用圖示表示如下:

縱觀初高中函數部分的學習,課本的編排也是符合以上人們認識客觀事物對象的思維方式的:首先初中課本通過具體反比例函數、一次函數、二次函數,反映函數“變量說”,即為感性具體;其次高中課本由3個實例導入,抽象出函數共同的本質屬性,函數“對應說”由此產生,進而從一般角度抽象出函數的基本性質,即為理性抽象;最后把各種抽象的規定通過更深層次的加工來把握具體的基本初等函數,即為理性具體。因此,我們的教學也應該遵循這一思維認知過程。
感性具體和理性具體是思維發展過程中的兩個不同階段,但他們有著本質的不同:感性的具體是零散的,是“知其然,不知其所以然”;理性的具體則是把事物各個抽象的規定綜合為一個相互聯系、相互制約的整體,是對事物完整的的認識[2]。
抽象是數學區別于其他學科的主要特點,《普通高中數學課程標準(實驗)》中強調,在具體教學中,要引導學生經歷從具體到抽象,概括事物本質屬性而獲得函數概念,在運用中形成知識網絡[3]下面圍繞思維方式上抽象與具體之間的轉化,我們將函數抽象性問題分為如下幾類:
2.1 具體——抽象——具體
有些函數問題已知條件明確具體,若用常規辦法處理會導致非常繁瑣,若能結合條件把問題抽象,上升到一般角度,考慮函數抽象性的性質表征,再從性質出發解決具體函數問題,往往能收到意想不到的效果,我們稱這個過程為具體函數抽象化。
分析: 此題可直接代入計算,但運算量巨大易錯,注意到所求中自變量互為相反數,我們可以研究此具體函數的定義域及奇偶性,得到?x∈(-1,1),都有f(-x)=-f(x),即f(x)+f(-x)=0,從而得解。

2.2 抽象——具體——抽象
與上一類問題相對的是,題中條件均抽象不具體時,倘若能把抽象函數具體化、圖形化,通過自然語言表述加工轉化,可能會收到意想不到的結果,打開解題思路,我們稱這個過程為抽象函數具體化,通常采用的方法有:變量賦值具體化、函數圖形具體化、函數解析式具體化。
例2 已知函數f(x)的定義域是(-∞,0)∪(0,+∞),對定義域內的任意x1,x2,都有f(x1x2)=f(x1)+f(x2),且當x>1時f(x)>0,f(x)=1,求證:f(x)是偶函數
分析:深入分析f(x1x2)可知,只需證f(-x)=f(-1)+f(x)即可,所以重點思考f(-1)=0,即證f(1)=0,此時結合條件將x1,x2均具體化為1,即找到解題思路。也可結合f(x1x2)=f(x1)+f(x2)將函數解析式具體化為f(x)=log2|x|分析。
通過抽象函數具體化只是為了找到題目解決的切入點、突破口,即通過具體函數的解析式、圖像來推測抽象函數的性質,同時也要注意不能完全代替應用,要把握分寸,防止以偏概全的解決問題。
2.3 純抽象性問題
解決純抽象性函數問題要求學生有較完備的知識結構,有一定的解題經驗,充分利用數形結合、轉化劃歸等數學思想,是對學生綜合素質的鍛煉與提高。除此之外,還要求學生能從眾多條件中把握此函數最本質性質,并深入分析應用,重視知識點的交匯處,善于利用函數圖像的抽象表征。
例3 設f(x)在(-∞,+∞)上滿足f(2-x)=f(2+x),f(7-x)=f(7+x),且在閉區間[0,7]上只有f(1)=f(3)=0.(1)試判斷函數f(x)的奇偶性;(2)試求方程f(x)=0在閉區間[-2005,2005]上根的個數,并證明你的結論。
分析:從條件中不難得到函數的周期、對稱軸、零點等信息,若學生能據此簡單勾畫出函數草圖便可得出函數為非奇非偶函數,明確解題方向:欲證非奇非偶只需利用周期性找一特殊位置說明函數沒有對稱性即可,如(-3,f(-3))與(3,f(x));同樣,零點個數問題,也是結合草圖利用周期性證明函數在[4,7]和[7,10]上無零點,在[0,10]上只有1和3兩個零點。
以上是從函數解題時思維發生發展的角度,對函數問題進行分類,探尋在解題中如何將抽象化與具體化相結合來降低函數抽象性帶給學生的認知障礙,以期尋找克服函數因其抽象性而難教難學的有效解決策略[4]。
[1]鄭正亞·數學抽象概念教學隨筆[J].數學教育學報, 1999(1):75-78.
[2]史寧中·數學的抽象[J].東北師大學報哲學社會科學版, 2008(5):169-169.
[3]中華人民共和國教育部·普通高中數學課程標準(實驗)[M].北京:人民教育出版社,2003.
[4]王康·高一數學函數抽象性教學研究[M].山西:山西師范大學,2014.
(責任編輯:王德紅)
Analysis of the Function Categorization form the Perspective of Abstractness
Wang Kang
(Lvliang College Fenyang Teachers’ School Branch,Fenyang 032200,Shanxi,China)
Analysing the abstract characteristics of the function from the perspective of variation of thinking modes towards the concrete objects, the paper focuses on the categorization of the function so as to find the best strategy to tackle the issue of abstractness of the function.
function,abstract,thinking modes
2016-09-10
王康(1982~),男,呂梁學院汾陽師范分校講師,碩士。研究方向:基礎數學。
G634.6
A
1673-9507(2016)06-0115-03

