GNSS偽距粗差的開窗探測及修復
周承松,劉文祥,肖 偉,彭 競,王飛雪
(國防科學技術大學,湖南 長沙 410073)
GNSS偽距粗差的開窗探測及修復
周承松,劉文祥,肖 偉,彭 競,王飛雪
(國防科學技術大學,湖南 長沙 410073)
針對GNSS偽距觀測粗差,提出一種基于同一衛星歷史偽距時間序列的時間相關性、不同衛星偽距間的空間相關性的開窗粗差探測修復方法。以窗口內歷史偽距時間序列分別預測當前各衛星偽距,得到各衛星偽距預測值和實測值的殘差并將其標準化,再用各衛星偽距殘差的變異系數來衡量不同衛星偽距間的空間相關性,通過偽距時間相關性和空間相關性構成膨脹因子進行粗差定位,并以窗口內偽距相關為原則進行粗差修復。試驗證明,該方法能在線探測修復多種類型偽距粗差,并能合理處理不影響定位的等量跳變。
偽距粗差;開窗探測修復法;時間相關性;空間相關性;變異系數
衛星導航觀測量的粗差探測修復,尤其是多個粗差的探測修復,是衛星導航接收機完備性監測的研究熱點[1-2]。衛星導航中,只有準確獲取偽距觀測值的精度和偏差信息才能保證定位精度[3]。由于受衛星姿態、空間環境、觀測環境及接收機噪聲等的影響,偽距觀測值難免存在粗差。對偽距粗差進行探測修復是有必要的,而國內外學者的研究對偽距粗差的探測修復關注較少,主要集中在載波相位的周跳探測修復上,逐漸出現了高次差法、電離層殘差法、多項式擬合法、多普勒積分法、偽距相位組合法、擬準檢定法、小波分析法、卡爾曼濾波法等周跳探測修復方法[4-6]。
較為常見的偽距粗差探測方法有:偽距相位組合法、偽距定位殘差判斷法。前一種方法不容易區分粗差是源于偽距粗差或載波相位周跳,后一種方法在多顆衛星偽距觀測量同時出現粗差時將難以定位[3]。而本文方法是基于歷史偽距時間序列的時間相關性和不同衛星偽距間的空間相關性進行偽距粗差的實時探測與修復的。
一、開窗探測修復法
要使得開窗粗差探測修復法奏效,就必須利用窗口內偽距信息精準地定位粗差,再利用窗口內偽距的互相關性進行粗差修復。該方法主要涉及窗口長度設置,偽距的時間相關性、空間相關性探測,粗差修復3方面內容。
1. 時間相關性探測
時間相關性探測,即利用窗口內同一衛星的歷史偽距時間序列預測當前偽距,并對當前偽距實測值進行合理性檢驗。利用當前歷元k的前l個歷元(窗口長度為l)的偽距值擬合預測當前偽距,再獲取偽距預測值和實測值的殘差,并將偽距殘差標準化使其服從標準正態分布,最后進行粗差的時間相關性探測,具體過程為
(1) 多項式擬合預測
(1)

(2) 最高階數n的確定
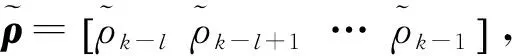
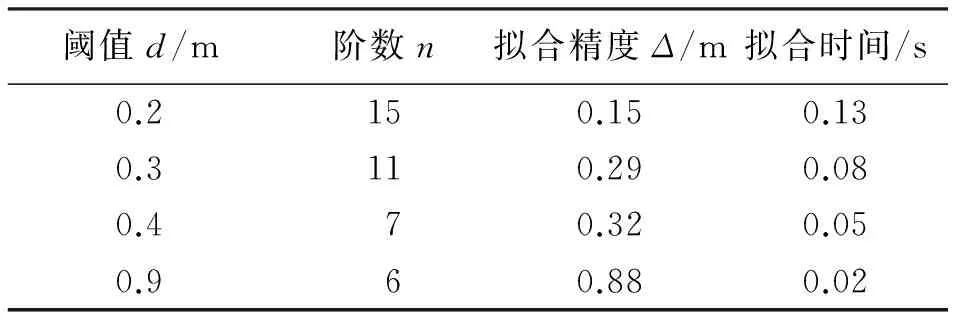
表1 n、d、Δ與擬合時間關系
分析表1可得,閾值越小,階數越高,擬合精度越高,但擬合時間越長,實際應用中應綜合考慮。考慮到偽距的量級較大,其擬合精度在米級即可,因此本文中n取6。
(3) 偽距殘差
(4) 偽距殘差標準化
(2)
(5) 時間相關性探測

2. 空間相關性探測

等量跳變一般幅度較大,但由于是跳變時等量的,故各衛星偽距殘差的離散程度很小,因此空間相關因子能衡量其離散程度即可。由于不發生跳變與發生跳變時各偽距殘差的均值不同,對于均值時變序列的離散程度,用標準差來衡量顯得不合理,變異系數是標準差與均值的比值,常用來衡量均值時變序列的離散程度,故本文以當前各偽距殘差的變異系數作為空間相關因子ck,即
(3)

3. 時間與空間相關性探測的融合
偽距粗差探測應綜合考慮偽距時間相關性和空間相關性,故時間相關性探測和空間相關性探測的融合是關鍵之一,融合原則是:當由時間相關性探測到粗差時,若由空間相關性未探測到粗差,則認為偽距發生等量跳變,若由空間相關性也探測到粗差,則認為存在粗差;當由時間相關性未探測到粗差時,則不考慮空間相關性探測,認為未探測到粗差。根據該融合原則建立探測偽距粗差的膨脹因子w,即
(4)

(1) k0的確定
考慮到空間相關因子為變異系數,是標準差與均值的比,其值不超過k0則認為當前數據穩定合格,這在工業制造、醫學等行業也有廣泛應用。在白細胞過氧化物傳感器研制中,制備固定細胞膜的重現性變異系數為5.5%[7];在《實驗室質量控制規范》(GBT 27404—2008)中,根據成分濃度的不同其變異系數閾值變動在1.3%~43%。另外,當所有衛星偽距出現等量跳變時其變異系數往往較小,理論上應將k0設小一點以便能更好地識別等量跳變。因此根據實際情況和變異系數的數學性質,本文k0設為0.1。
(2) k1的確定
k1值應根據觀測量的特點進行選取,通常選2.5~8.0。對于大地測量,因有較強的幾何檢核,選3.0左右合適;對于衛星激光測距和衛星偽距觀測值,選8.5左右為宜[8]。綜合考慮,本文k1設為8。
4. 粗差修復
定位粗差后,需要修復粗差。修復粗差是為了減小當前粗差對后續歷元偽距預測及粗差探測的影響,且面對連續粗差仍可穩健定位,當可視星少于4顆時也可直接用修復后偽距進行定位解算。粗差修復策略應充分考慮粗差的類型,本文從突變型粗差、連續型粗差著手,充分考慮多星同時且連續出現粗差等復雜情景,提出一種窗口內觀測相關修復法。
窗口內觀測相關性修復法,即認為窗口內的觀測量是相關的,并且離當前歷元越近的歷元,其觀測量與當前觀測量相關性越強。基于該觀點,詳細敘述本文修復策略。
(1) k歷元(即標桿歷元K)偽距修復
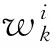
(5)
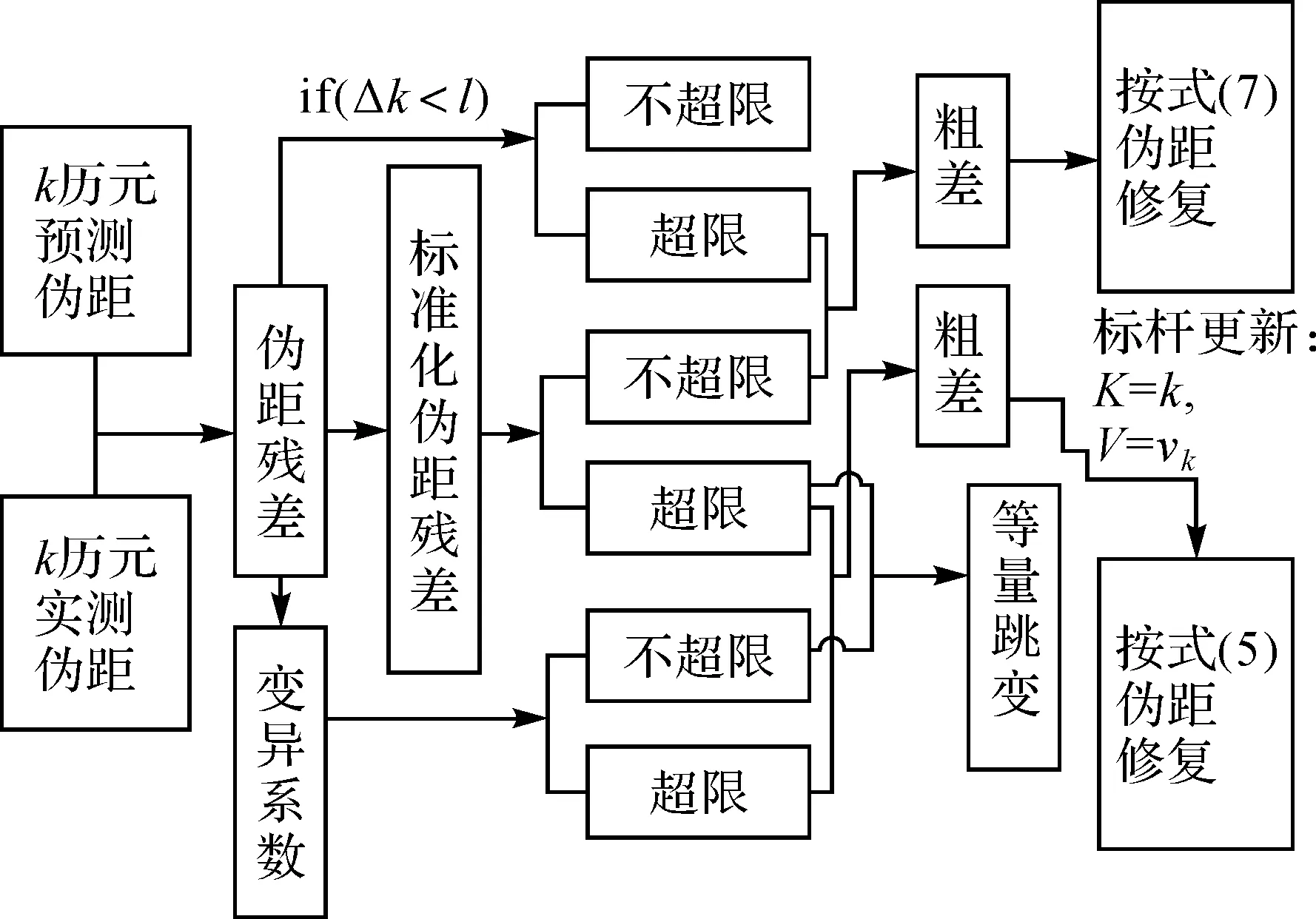
(2) K+Δk歷元偽距修復(Δk (6) 當K+Δk歷元滿足式(6)中的條件a時,按式(5)修復偽距;滿足條件b時,考慮窗口內觀測相關性,按式(7)修復偽距。 (7) 式中,ρK+Δk為K+Δk歷元的偽距觀測量;vK+Δk為歷元K+Δk的偽距殘差。從式(7)中可看出,Δk越大,K+Δk歷元的偽距修復與K歷元相關性越弱。 (3) K+Δk歷元偽距修復(Δk≥l) 當Δk≥l時,則繼續按步驟(1)、(2)修復偽距。流程歸納如圖1所示。 圖1 開窗探測修復流程 為分析本文修復方法的特點,現與兩種傳統修復方法作比較:一是當出現粗差時,直接以偽距預測量作為修復值;二是以偽距預測量和觀測量的均值作為修復值。分別在81、101~105 s的北斗1號星偽距觀測量上加入10 m的粗差,在3種修復方法下,修復后偽距與參考偽距的差值見表2。 表2 修復后偽距與參考偽距的差值 m 從表2可看出,傳統法在出現突變型粗差時的修復效果和本文方法相同,但在出現連續型粗差時效果遠不如本文方法。因此,本文修復法的性能較優。 關于偽距時間序列的窗口長度l的選取往往是個難題,近幾年來受到了學者關注,實踐中通常設為經驗值[9-10]。窗口長度過長,需存儲大量歷史偽距信息,且太舊的偽距信息對當前偽距預測的作用不大,而且其誤差反而會影響當前預測;但窗口長度過短,窗口內偽距的誤差對當前預測的影響無疑增大了。因此,窗口長度理論上存在最優值。 (8) (9) 式中,窗口內各偽距對當前偽距預測值包含兩類誤差:一是偽距觀測誤差vρ,二是偽距增量誤差vΔρ。平滑法中也存在類似本文擬合預測的窗口選擇問題,窗口過長,存儲量大,偽距增量誤差增大;窗口過小,難以平滑準確。當偽距增量誤差未積累到一個不可忽略的影響時,窗口越長越好,故在理論上,其窗口也存在最優值。 平滑法中,窗口內的偽距與當前偽距的關聯性越強,其在平滑過程中的重要性越大,最優窗口就是要判斷一個截點,剛好使得截點之外的歷史偽距與當前偽距基本不相關;本文對當前偽距的預測過程中,也是需要判斷這么一個截點,剛好使得截點之前的偽距對預測過程作用甚微,可有可無。因此,可近似地將本文擬合預測的最優窗口與平滑法的最優窗口等同。 現求取平滑法的最優窗口。由式(8)和式(9)可得,當前偽距最終預測的誤差ε為 (10) 則當前偽距最終預測誤差ε的均方根誤差平方值為 DRMS2=E[(Q+R)T(Q+R)]= E(QTQ+QTR+RTQ+RTR) (11) 為求取窗口l的最優值,將DRMS2對窗口l求導后令其等于零,解出的窗口l為最優值。假設式(9)中的偽距增量由當前載波相位與歷史載波相位相減求得,以k-l+1歷元為例,偽距增量Δρk-l+1=φk-φk-l+1,則偽距增量誤差vΔρk-l+1近似等于兩歷元載波的載波噪聲差和相應的電離層延遲變化量,而對流層延遲等誤差被消去了。由于載波與偽距受電離層延遲的影響具有大小相等,符號相反的特點,因此vΔρk-l+1包含的電離層延遲變化量是兩歷元間電離層延遲變化量的2倍,即vΔρk-l+1=(vφk-vφk-l+1)-2(l-1)idot,則 (12) 式中,vφ是載波噪聲;idot為1s的電離層延遲變化量,近似為不變量。由于載波噪聲遠小于偽距噪聲,可忽略不計,只考慮電離層延遲變化量,則 R≈-(l-1)idot (13) (14) (15) 為了驗證本文方法處理多類型粗差和等量跳變的能力,設計兩次試驗。 1) 試驗1:一種良好的粗差探測修復方法往往能適應多種類型的粗差。為驗證開窗探測修復法的性能,分別在偽距原始觀測量中加入突變小粗差、突變大粗差、等量連續小粗差、等量連續大粗差、緩變連續小粗差、緩變連續大粗差等多種類型粗差。試驗數據為2016年5月4日用GNSS信號源模擬動態跑車數據,頻點為北斗B3頻點,時長3837s,采樣間隔1s。分別在1號星偽距原始觀測量的前后27處加入不同類型的粗差,經過本文探測修復方法作用后,粗差探測情況參考膨脹因子,如圖2所示,修復情況如圖3所示。 圖2 1號衛星膨脹因子 圖3 粗差修復效果 從圖2可看出,提出的開窗探測修復方法能有效探測多種類型誤差;從圖3可看出,該方法對突變型和連續型粗差的修復能力最強,對緩變型粗差修復能力稍差,但也能較好地剔除粗差。 2) 試驗2:根據GNSS偽距特點,同一歷元所有衛星偽距發生等量跳變時,不影響定位,因此這種跳變不應作為粗差。傳統的探測修復方法會將其作為粗差處理,而本文開窗探測修復法能準確識別這種跳變,現以試驗說明。試驗數據、加入偽距跳變的歷元都與試驗1相同,只是在這些歷元的所有可視衛星偽距原始觀測量上加入100m等量跳變。經本文方法處理后,所有可視衛星的膨脹因子如圖4所示。 從圖4可看出,雖然在部分歷元的所有可視衛星偽距觀測中加入了100m的等量跳變(不影響定位),但利用本文方法求出的所有衛星的膨脹因子均未超過閾值k1(k1為8),從而不將這類跳變視為粗差,這是合理的。因此本文方法能正確處理這類跳變。 針對GNSS偽距的特性,本文提出了一種基于同一衛星歷史偽距時間序列的時間相關性、不同衛星偽距間的空間相關性的開窗探測修復方法。試驗證明,該方法能有效探測及修復突變型、連續型、緩變型等偽距粗差,并能合理處理由接收機校時等原因引起的所有可視衛星偽距的等量跳變現象。 圖4 所有衛星膨脹因子 [1] 吳云.GNSS粗差檢測的“快照”法與“濾波”法的比較研究[J].武漢大學學報(信息科學版),2010,35(6):649-652. [2] 沙海,黃新明,劉文祥,等.基于非相干積累的微小偽距偏差RAIM方法研究[J].宇航學報,2014,35(6):708-712. [3] 王甫紅,劉基余.星載GPS偽距測量數據質量分析[J].測繪科學技術學報,2007,24(2):97-99. [4] 李金龍,楊元喜,徐君毅,等.基于偽距相位組合實時探測與修復GNSS三頻非差觀測數據周跳[J].測繪學報,2011,40(6):718-729. [5] 龔學文,王甫紅.低軌衛星星載GPS數據偽距粗差及相位周跳探測與分析[J].測繪通報,2016(2):17-21. [6] 劉文祥,李崢嶸,王飛雪.一種可檢測和改正微小慢變偽距偏差的新RAIM方法[J].宇航學報,2010,31(4):1024-1029. [7] 那曉琳,張宏緒.白細胞過氧化物傳感器的研制[J].傳感技術學報,1995,8(2): 39-43. [8] 楊元喜.自適應抗差最小二乘[J].測繪學報,1996,25(3):206-211. [9] 楊元喜,徐天河.基于移動開窗法協方差估計和方差分量估計的自適應濾波[J].武漢大學學報(信息科學版),2003,28(6):714-718. [10]GUOJF,OUJK,YUANYB.OptimalCarrier-smoothed-codeAlgorithmforDual-frequencyGPSData[J].NaturalScience,2008(18):591-594. [11] 尚書亮,李銳,黃智剛.利用卡爾曼濾波估計導航信號電離層差分改正[J].武漢大學學報(信息科學版),2010,35(9):1021-1023. GNSS Pseudo-range Outlier’s Detection and Reparation Based on Moving Window ZHOU Chengsong,LIU Wenxiang,XIAO Wei,PENG Jing,WANG Feixue 周承松,劉文祥,肖偉,等.GNSS偽距粗差的開窗探測及修復[J].測繪通報,2016(12):20-24. 10.13474/j.cnki.11-2246.2016.0393. 2016-06-15 國家自然科學基金(61403413) 周承松(1991—),男,碩士生,主要研究方向為GNSS數據處理。E-mail:whunudter@whu.edu.cn P228.4 B 0494-0911(2016)12-0020-05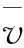

二、窗口確定



三、試驗分析


四、結束語


