時空約束性GeoCA模型在城市土地利用預測中的應用

程寶銀，杜 陽

(蘇州市測繪院有限責任公司，江蘇 蘇州 215000)

時空約束性GeoCA模型在城市土地利用預測中的應用

程寶銀，杜 陽

(蘇州市測繪院有限責任公司，江蘇 蘇州 215000)

通過在傳統GeoCA(地理元胞自動機)模型的基礎上添加時空影響因素，建立了時空約束性GeoCA模型，對城市土地利用變化進行了預測;在保證土地利用類型轉化率精度的前提下，兼顧了時間跨度因素和鄰近用地分布因素的影響，實現了真正意義上的土地利用變化預測。

GeoCA；GIS；時空；土地利用

隨著城市經濟的發展和人口數量的加劇，城市土地資源相對減少，帶來的住房緊張、生態失衡等問題日益突出。因此，城市土地資源的優化配置和合理規劃成了熱門研究課題，吸引了眾多學者的關注。在相關研究中，具有代表性的成果有荷蘭赫寧根大學研制的CLUE-S模型、美國麻省理工學院創建的SD(system danamics)模型、Ulam提出的CA(cellular automatic)模型，以及國內黎夏、張顯等提出的地理元胞自動機模型等[1]。這些模型可有效模擬復雜土地利用的變化過程，為土地的動態預測研究作出了突出貢獻。研究表明，基于BP-ANN(back-propagation artificial neural network)算法的GeoCA模型可較好地模擬我國城市土地利用變化過程[2]。本文在此基礎上，提出時空約束性GeoCA模型，在考慮土地數量變化的同時，可兼顧影響土地變化的空間和時間因素，彌補以往做法中未能有效考慮土地利用變化時間和土地類型空間分布規律的不足。

一、模型應用原理

時空約束性GeoCA模型在土地利用變化模擬中的應用原理是以柵格數據表示土地在不同時刻的利用狀態信息，通過研究影響其利用狀態變化的各類因子及其之間的關系，定義土地利用信息的轉化規則，從而建立起轉化模型，對土地利用變化進行模擬和預測。它與傳統GeoCA模型的本質區別在于加入了影響土地利用變化的時間跨度因素及各類影響因素的空間分布因素，可以更真實地反映土地在不同時空影響因素作用下的利用情況。該模型可用如下數學表達式進行描述

GCA=(C,S,F,R,T)

(1)

式中，GCA為地理元胞自動機；C為代表某一用地實體的用地元胞；S為元胞C的利用狀態；F為引起元胞C狀態發生轉變的影響因素集合；R為轉換規則，即F對C的影響關系；T為元胞C的時間維，規定在某一時刻T，用地元胞的利用狀態S唯一。其中，影響因素F的提取和轉換規則S是模型研究的核心內容。該模型工作原理的圖形表達如圖1所示。

圖1 時空約束性GeoCA模型工作原理

圖中以3×3的元胞研究范圍為例，對中心元胞C的狀態轉換進行研究。T時刻元胞的土地利用狀態為S，用紅色表示，不同的顏色代表不同的土地利用狀態；中心元胞周圍的其他8個土地元胞及FR(道路)、FW(水域)、FC(市中心)等為影響因素集合F中的因素，圖中SR、SW、SC分別為中心元胞C到FR、FW、FC的最短距離；在轉換規則R的作用下，經過t時間，土地元胞C轉變為T+t時刻的狀態。

二、數據處理方法研究

1. 數據分析

使用時空約束性GeoCA模型進行土地動態模擬，首先需要利用已知數據構建模型并驗證模型的正確性，在此基礎上進一步預測土地利用變化。從模型的工作原理可知，模型構建所需要的基礎數據包括至少3期的研究區域土地利用柵格數據及各種影響因素。相關研究表明，影響土地利用變化的因素通常包括一系列的距離變量、鄰近土地利用類型及分析單元的自然屬性[3]。由于土地利用變化不僅受各類要素數量的影響，同時還受空間布局及時間跨度的影響，因此本文在此基礎上加入了時間因素和空間因子的分布因素進行研究。

2. 數據處理

獲取研究區土地利用柵格數據的方法有多種，各類影響因素中時間要素可利用時間參數表示，空間變量則需從土地利用數據中提取。由于ArcGIS具有強大的空間數據處理與分析能力，且在Arc/Info Grid環境中內置了Eucdistance等函數，便于空間距離變量及元胞周圍用地類型的提取和模型的程序實現，因此選擇在ArcGIS中完成數據處理工作。研究所需數據類型及其處理方法詳見表1。

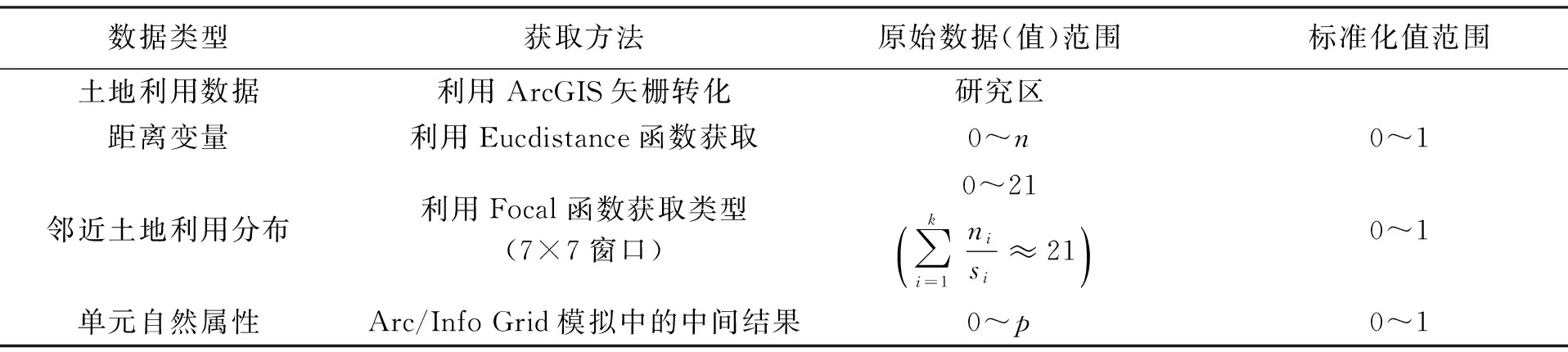
表1 模型所需數據及其處理情況

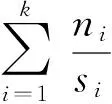
三、轉化規則研究

1. 轉換規則算法基礎

構建合理的GeoCA模型涉及的參數眾多，需對模型進行反復糾正，獲取合適的模型參數。土地變化的研究基于眾多離散型變量，很難用一個數學公式表達。研究表明，神經網絡算法特別適用于模擬復雜的非線性系統，因此本文試圖采用BP-ANN算法研究多種土地利用變化的轉換規則。

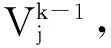
(2)

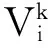
(3)

(4)

為使誤差r取得極小值，則需要使權值朝著誤差函數的負方向變化，設Δωij為ωij的變化量，則

(5)

式中，ε為學習步長，且ε>0。推導可得

(6)

設

(7)

則

(8)

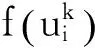
(9)

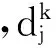
2. 基于BP-ANN算法的轉換規則研究

本研究選用3層神經網絡結構(輸入層、隱藏層、輸出層)，假設對于每一個用地元胞，有N個影響變量，分別用x1,x2,…，xn表示，這些變量分別對應第1層神經網絡的N個神經元，它們共同作用決定了該用地元胞的用地屬性，用下式進行描述

X(k,t)=[x1(k,t)x2(k,t)…xn(k,t)]T

(10)

式中，xi(k,t)表示單元k在模擬時間t時的第i個變量；T表示轉置。根據BP-ANN算法，中間層第j個神經元接收到的總輸入為

(11)

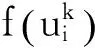
(12)

式中，P(k,t,l)表示k單元在模擬時刻t從現狀轉化為l類型的概率。在每次循環中計算出每個神經元轉換為N種不同用地類型的轉換概率，由于某一用地元胞在某一時刻的用地狀態唯一，因此可以根據轉化概率最大值確定該元胞最終的轉換狀態。

四、模型應用

以江蘇某市的土地利用預測為例，獲取試驗區2011年、2012年、2015年3期土地利用數據進行研究。研究區的用地類型分為建成區、工業用地、交通用地、建設用地及耕地等9種用地類型；提取了距市中心距離、公路距離兩種距離變量及坡度一個自然單元屬性。將2011年的試驗區用地數據作為初始狀態，分別取2012年和2015年的樣本數據獲取模型參數，對2015年用地分別模擬出基于非時空約束GeoCA模型、基于時間約束性GeoCA模型、基于空間約束性GeoCA模型及時空約束性GeoCA模型4種情況下的模擬預測，并與2015年試驗區的真實用地數據進行對比，效果分別如圖2—圖7所示。

通過對用地類型分類模擬圖與實際分類圖進行對比可以看出，基于時空約束性GeoCA模型模擬的結果在轉化率和空間分布上與實際狀況比較一致；基于非時空約束性GeoCA模型模擬的結果在某些類型模擬中轉化率差距較大(如水域)，且空間分布吻合性差；僅基于時間約束的GeoCA模型模擬的結果轉化率與實際較吻合，但空間分布吻合性最差；僅

基于空間約束的GeoCA模型是基于2012年的訓練參數與對2015年的用地進行模擬，結果發現跨度縮小為1年后，各類用地與2011年變化量最小，與2015年變化量最大。綜合上述分析，可以驗證本文研究模型的有效性。

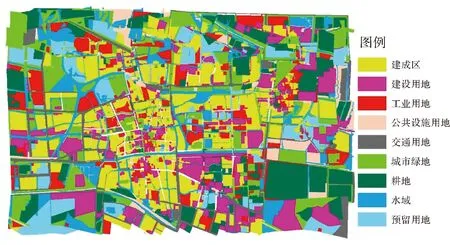
圖2 2011年某市土地利用實際分類結果

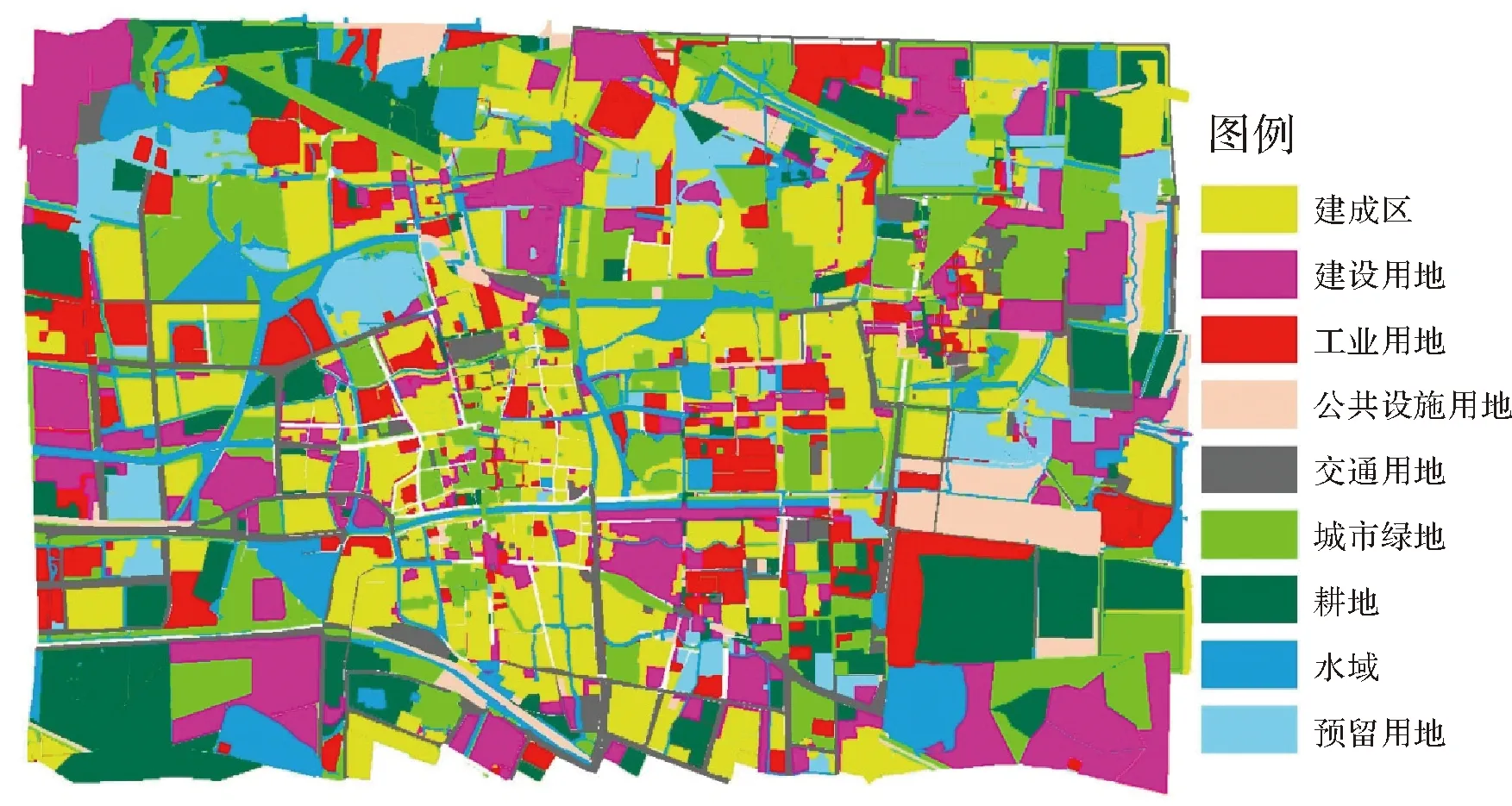
圖3 非時空約束性GeoCA模型預測結果

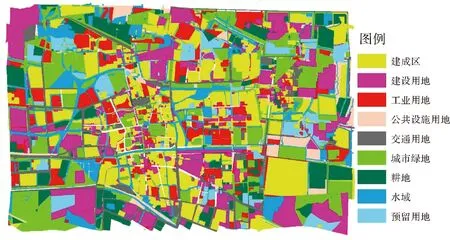
圖4 時間約束性GeoCA模型預測結果

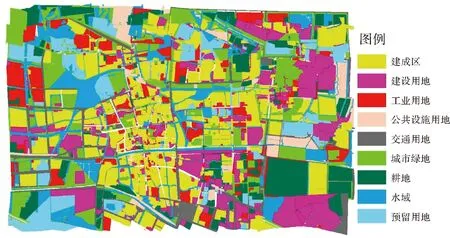
圖5 空間約束性GeoCA模型預測結果

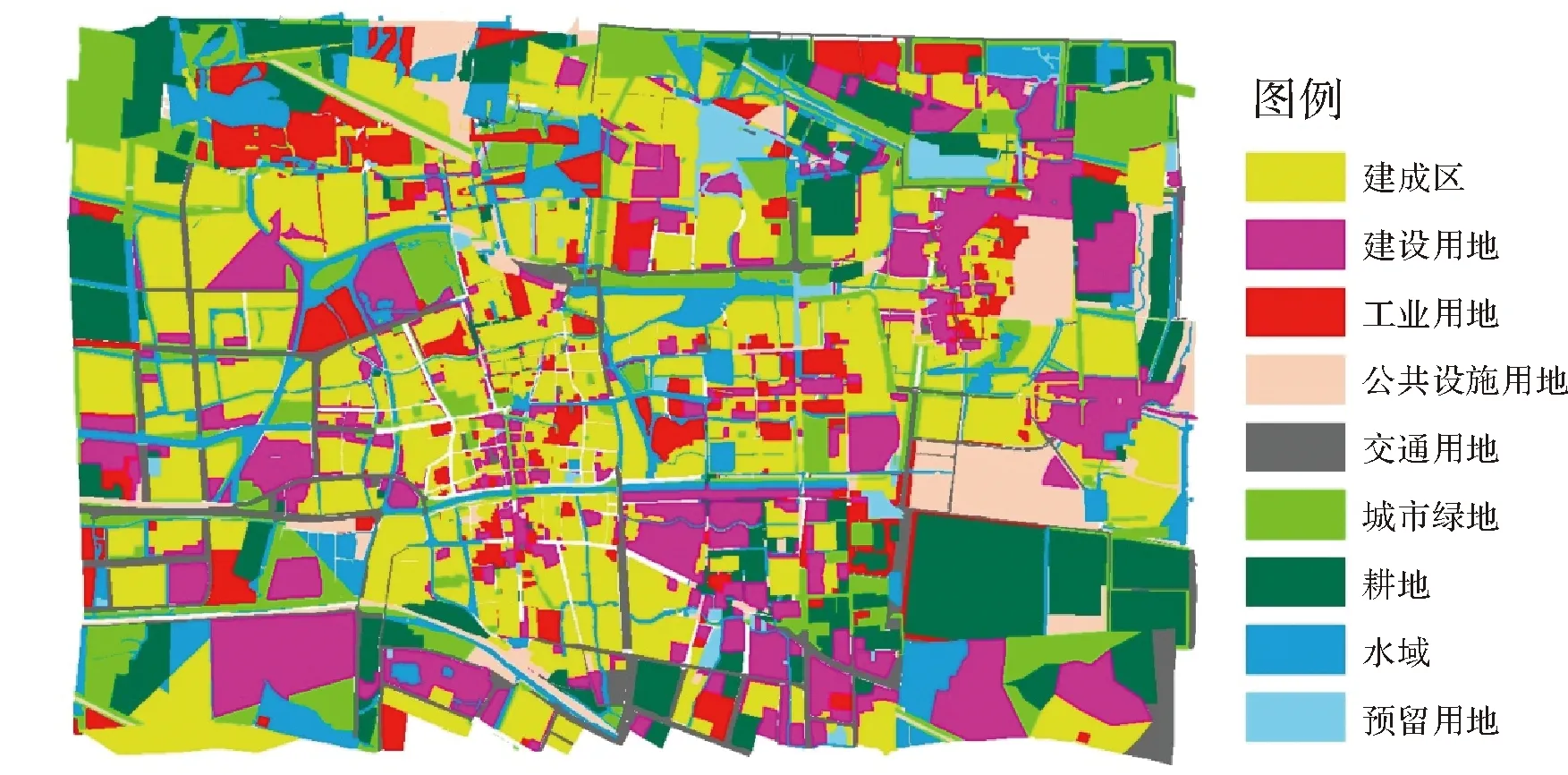
圖6 時空約束性GeoCA模型預測結果

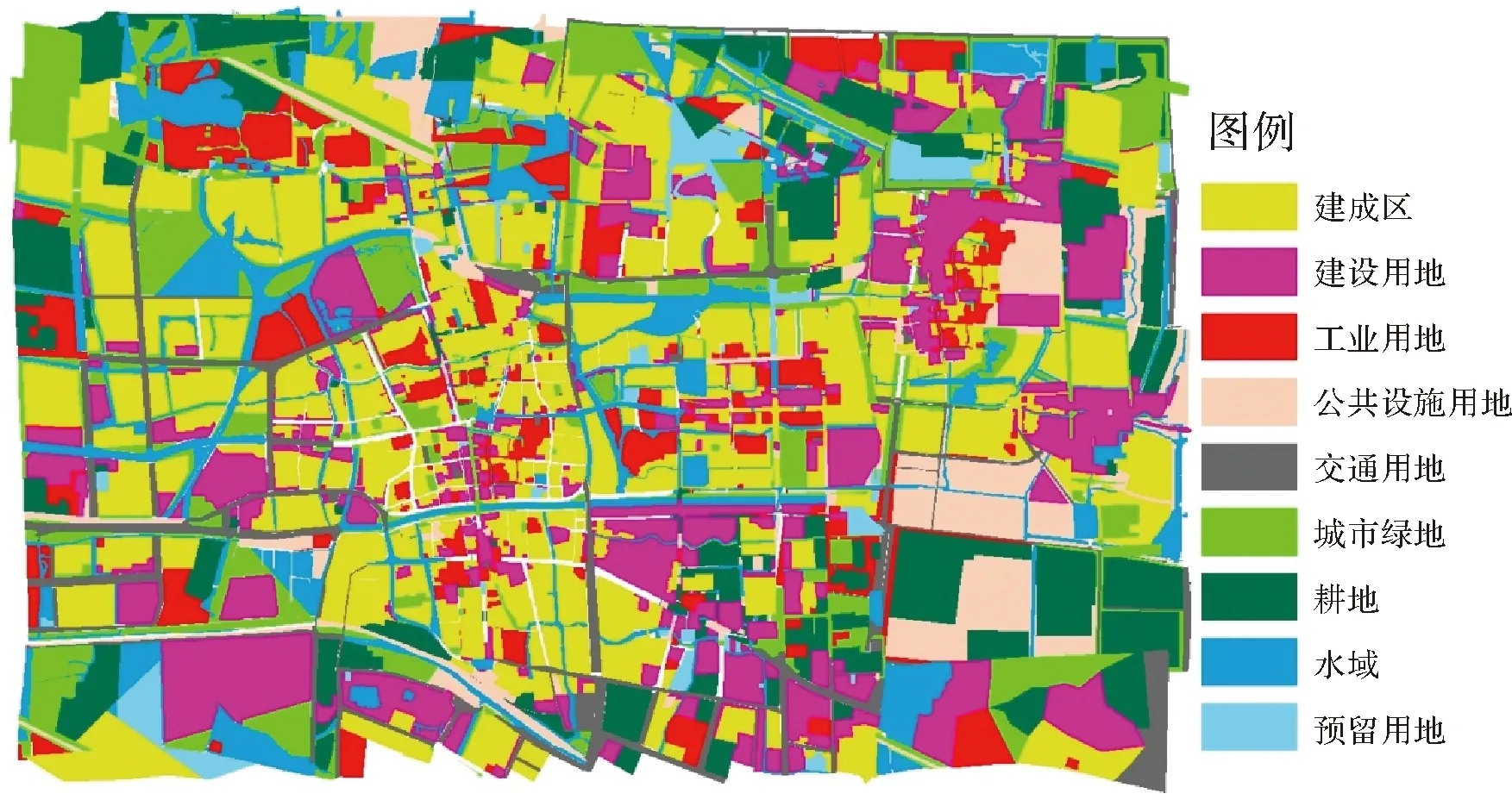
圖7 2015年某市土地利用實際分類結果

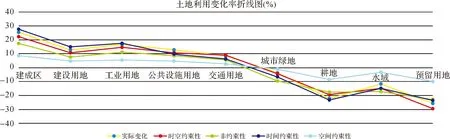
圖8 土地利用變化統計折線

五、結束語

傳統的GeoCA模型為土地利用動態預測研究做出了重大貢獻，本文在此基礎上加入了時空影響因素，在考慮土地利用轉化率的同時，兼顧了時間和土地利用類型分布對土地利用變化的影響，并通過實際案例驗證了模型的有效性。不同區域土地利用變化的影響因素不同，因此研究適合本地的時空約束性GeoCA模型還需針對區域的特點作更加詳細的研究，從而為當地相關部門提供科學的決策支撐。

[1] 周成虎，孫戰利，謝一春.地理元胞自動機研究[M].北京：北京出版社，1999：128-137.

[2] 黎夏，劉小平，李少英.智能式GIS與空間優化[M].北京：科學出版社，2010：37-130.

[3] BATTY M，XIE Y.From Cells to Cities.[J].Environment and Planning B，1994(21)：531-548.

[4] 王立波.基于GIS和Geo-CA的營口城市用地擴展模擬預測研究[D].長春：東北師范大學，2009.

[5] 李鳳霞，石輝，馮小剛，等.西安市土地利用格局動態演變及其驅動力研究[J].測繪通報，2015(12)：41-56.

[6] 邱小平，于丹，孫若曉，等.基于安全距離的元胞自動機交通流模型研究[J].交通運輸系統工程與信息，2015(12)：54-60.

[7] 陳建平，丁火平，王功文，等.基于GIS和元胞自動機的荒漠化演化預測模型[J].遙感學報，2004，8(3)：254-260.

[8] 劉衛芳，夏斌，聶云峰.基于GIS與多智能體的建設用地變化仿真研究——以廣州番禺區為例[J].安徽農業科學，2012，40(21):11083-11085.

[9] 王福增，尤麗敏，王凡.大連市土地利用現狀及變化分析[J].管理科學，2008，29(6):123-125.

Research of Temporal and Spatial Constraint GeoCA Model Applied in Urban Land Use Prediction

CHENG Baoyin，DU Yang

2016-01-08；

程保銀(1977—)，男，高級工程師，主要從事測繪地理信息方面的工作。E-mail:szchy@163.com

杜 陽

程寶銀，杜陽.時空約束性GeoCA模型在城市土地利用預測中的應用[J].測繪通報，2016(12)：116-119.

10.13474/j.cnki.11-2246.2016.0415.

P208

B

0494-0911(2016)12-0116-04

修回日期：2016-10-31