基于動荷載仿真的路面結構響應分析

侯靜

（天津城建大學 土木工程學院，天津 300384）

基于動荷載仿真的路面結構響應分析

侯靜

（天津城建大學 土木工程學院，天津 300384）

針對貨車動荷載作用下路面結構力學響應及路面設計指標變化規律，應用ABAQUS有限元軟件建立相應三維路面結構模型及動荷載模型進行動態模擬，并通過現場試驗驗證了模型的可靠性，對路表彎沉和各結構層層底應力情況進行計算，分析不同車速、平整度和路面結構參數對路面結構力學響應的影響，得到車速、平整度和路面結構參數對路面力學響應的影響規律，可以為路面結構設計和道路施工養護提供理論指導．

動荷載；平整度；動態模擬；有限元

近年來，隨著國家高等級道路和經濟貨運流通的快速發展，出現越來越多高速、密集、超載車輛，加大了對路面結構損傷程度，嚴重影響行車舒適性，使道路提前進入保養修護，導致整條道路甚至整個路網運行效率低下，造成不良社會影響和經濟損失．基于現場試驗，對貨車動荷載作用下路面結構力學響應及路面設計指標變化規律進行有限元模擬分析，可以更好模擬實際道路受力情況，為路面結構設計和道路施工養護提供理論指導．筆者采用多層彈性路面結構，建立了相應的車輛動荷載模型和路面結構模型，并對路面結構力學響應規律進行了模擬研究．

1 動荷載有限元模擬

1.1 荷載模型及參數

采用連續的半波正弦曲線作為動力加載函數來模擬實際汽車荷載，其表達式為：

式中：P0為車輛靜載，取車輛單邊輪載，單位kN；P為振動荷載幅值，，M0為車輛模型簧下質量，為振動圓頻率，， 為車速，L為路面幾何曲線波長，為路面幾何不平順失高（按國際高速公路平整度指數取值）．滿載30 t（超載42 t）三軸貨車其具體荷載計算參數如表1[1-2]．

1.2 路面結構模型及參數

基于彈性層狀體系理論，對滄州市典型省道路面結構進行模擬分析，試驗道路采用瀝青混凝土道路模型，其尺寸分別為長（Z方向）8m、寬（X方向）8m、高（Y方向）5m；車速取現場試驗車輛所測實際車輛的速度；單側雙輪輪胎當量接觸面積為0.24m2，輪胎接地壓力為0.7 MPa；平整度為現場所測實際道路平整度值15mm/3m，路面結構和相應材料參數如表2[3-4]（車輛動荷載作用下路面結構層材料模量變化較小，故采用靜態彈性模量，取值采用同類路面結構材料試驗測值），建立的有限元路面結構模型如圖1所示．

表1 荷載計算參數Tab.1 Load calculation parameter table

圖1 路面結構模型Fig.1 Pavementstructuremodel

表2 路面結構材料參數Tab．2 Pavementstructurematerialparameters

2 路面結構響應分析

2.1 不同車速下的路面結構響應

分別計算不同行車速度下路表彎沉最大值和基層層底拉應力最大值的變化情況，如圖2、圖3所示．

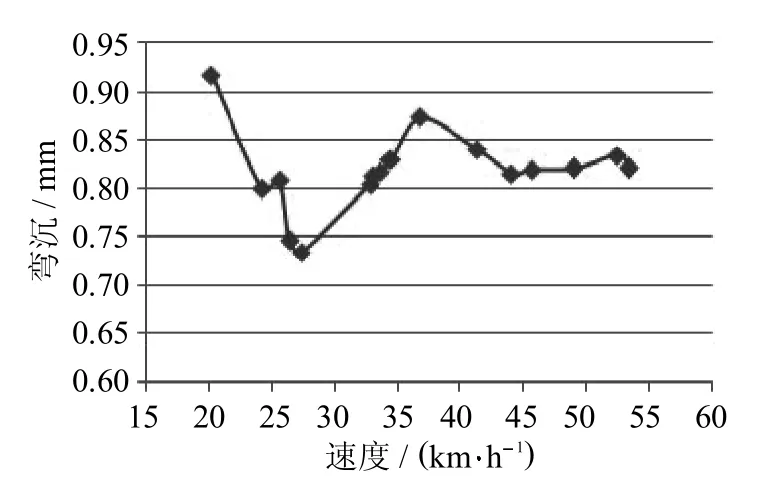
圖2 不同車速下路表彎沉Fig.2 Deflection changesunder differentspeeds

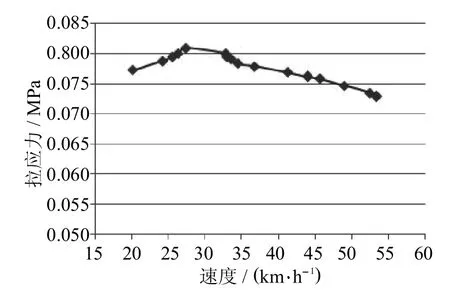
圖3 不同車速下層底拉應力Fig.3 Stressunder Differentspeeds

由圖2可以看到在較低速度時，路表彎沉值隨車速增長而降低，隨著速度繼續增大時，彎沉相應增加，但增大到一定程度后就基本保持平穩起伏，沒有太大的增減變化，相對于低速時的表現要穩定得多．

由圖3可以得隨著車速的增加盡管低速時拉應力有一些起伏，從整體來說還是減小的，但減小的幅度較小，只有10.1%．主要原因是在較平順道路上，汽車行駛所產生的沖擊作用處于較低水平上，盡管動荷載隨著速度增加有相應的變化，對面層應力作用較顯著，但對基層處應力變化作用較小，即在較平整道路上車輛行駛速度對基層底拉應力的影響作用不大[5]．

2.2 不同平整度下的路面結構響應

平整度等級選取平整度u為2mm、5mm、15mm、20mm、40mm、80mm，計算一定車輛行駛速度（40 km/h）下的路表最大彎沉值和基層層底最大拉應力值如圖4、圖5所示．

由圖4可以看到路表彎沉隨著道路平整度的增大而變大，基本呈線性增長趨勢，但其增長的幅度較大，前后增長了320%．主要原因在于路面平整度差時會增加車輛對路面的沖擊作用和與路面相互作用的振動接觸次數，進而對路面的彎沉作用會更大，所以保持較平順的道路平整度對于車輛對道路損傷破壞作用至關重要，故道路平整度是一個需要高度重視的影響因素．

由圖5可以看到基層底最大拉應力隨著平整度值增大逐漸增大，且增長幅度較大，在u=80 mm時較u=2mm時拉應力增長了66.6%，可見平整度的大小對基層底拉應力值有很大的影響作用，保持道路的平順可以有效地降低道路基層結構損傷破壞．

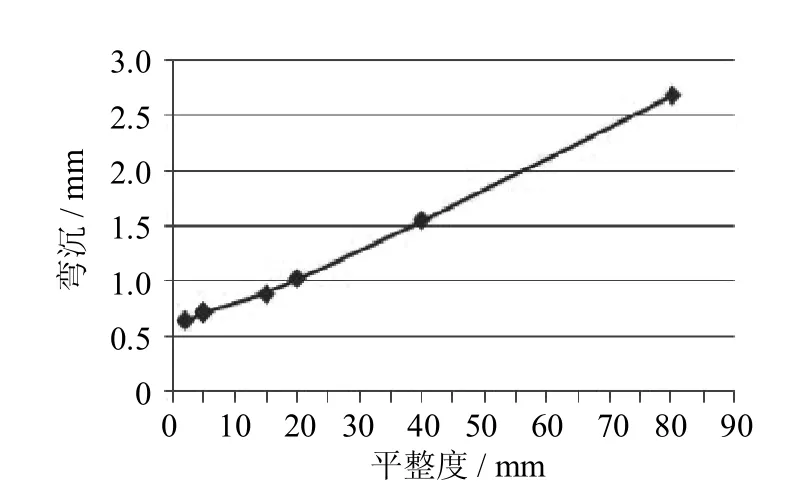
圖4 不同平整度下路表彎沉Fig.4 Deflection under different flatnessvariation

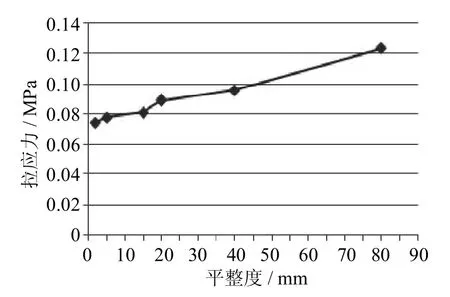
圖5 不同平整度下層底拉應力Fig.5 Stressunder different flatness

3 路面結構參數影響分析

3.1 各結構層厚度變化分析

對表2路面結構材料參數中各結構層厚度依次進行改變，每次都只改變一層的厚度，其他層厚度和其他材料參數保持不變，且每層結構都會由大到小線性原則改變3種厚度，具體的厚度設置參照表3所示，然后分別計算各結構層不同厚度時的路表最大彎沉和面層、基層底最大拉應力值的變化，如表4所示．

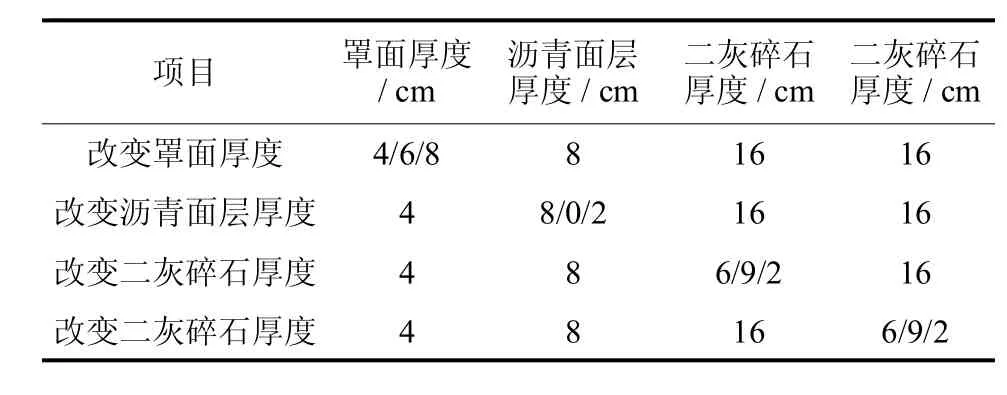
表3 厚度取值Tab．3 Thickness values

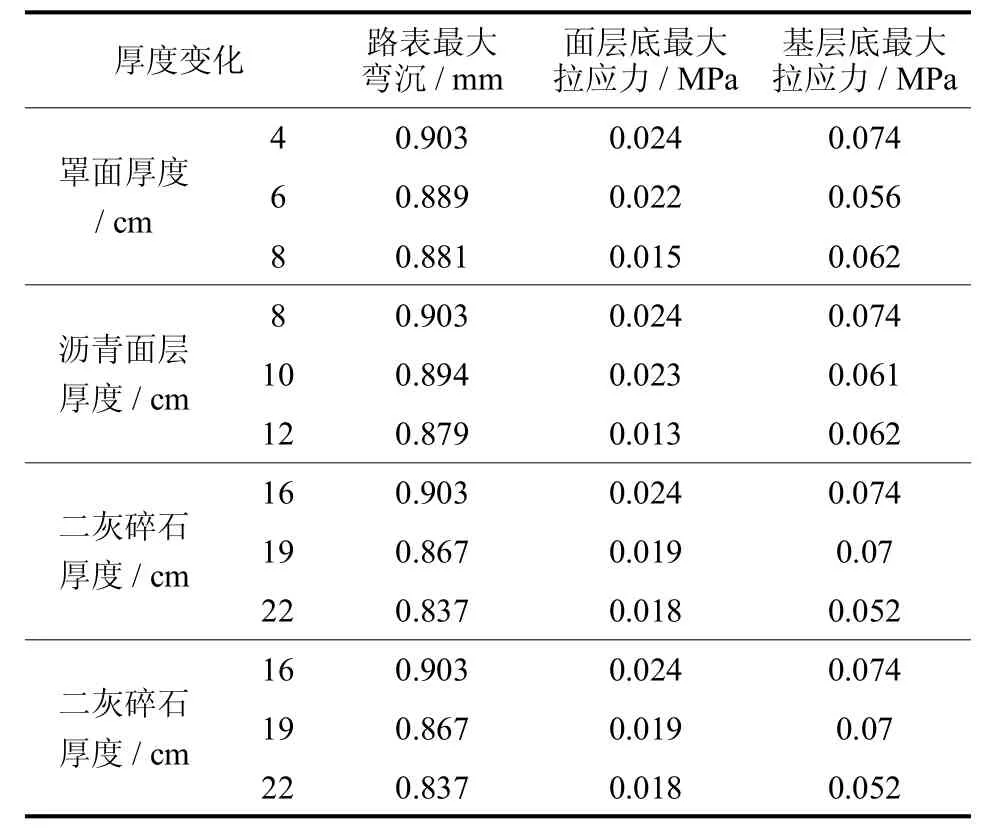
表4 厚度改變引起的變化Tab．4 Changes caused by thickness variation

通過表4的計算數據可以看到每一結構層厚度的增加都可以減小路表最大彎沉值，但減小的幅度不一樣，兩層二灰碎石基層對路表最大彎沉的影響最為明顯，主要是因為基層材料的模量相對較大且厚度基數比較大，所以其厚度的變化對路表的彎沉影響最大，然而罩面和面層厚度的增加對降低路表彎沉效果不大，不能作為降低控制路表彎沉的措施，同時從經濟角度考慮通過增加上面層厚度的方法來減小路表彎沉造價太高，是不經濟的措施，不適宜過大增加面層結構厚度來抵抗路表彎沉變形．

對于面層底最大拉應力，雖然增加各結構層厚度都可減小拉應力，但改變罩面和瀝青面層厚度效果較明顯，尤其瀝青面層增加自身厚度可以有效降低自身層底最大拉應力；對于基層底最大拉應力，增加各層結構厚度都可以減小拉應力，但兩層二灰碎石基層厚度的增加對減小拉應力作用最大，同樣也證明了增加本層厚度可以有效減小本層底最大應力值[6-7]．

3.2 各結構層彈性模量變化分析

對表2路面結構材料參數中各結構層材料彈性模量依次進行改變，每次都只改變一層材料的彈性模量，其他層材料彈性模量和參數保持不變，且每層結構材料彈性模量都會由大到小按照線性原則改變3種數值，具體的彈性模量設置參照表5所示，分別計算各結構層材料不同模量時的路表最大彎沉和面層、基層底最大拉應力值如表6所示．

通過表6所示的各結構層材料的模量變化對路表最大彎沉值和層底最大拉應力的影響可以得到，增加各結構層材料的彈性模量都可以減少路表最大彎沉值，其中土基彈性模量對減少路表彎沉值效果最明顯，主要原因是相對于路面各層結構厚度來說土基層厚度很大且位于最底層，可以有效的承載擴散上部傳來的彎沉效果；其次是基層材料，雖然可以有效減小路表彎沉，但減小的幅度不大且隨著基層模量增大到一定程度，路表彎沉減少的速度就明顯變慢．可見適當的提高路基彈性模量是減小路表彎沉的最有效辦法．

對于層底最大拉應力：增加罩面材料彈性模量，可以分別減小面層、基層底最大拉應力值；增加瀝青面層材料彈性模量，面層底最大拉應力增大，基層底最大拉應力值減小；增加二灰碎石基層材料彈性模量，面層底最大拉應力減小，但幅度不大，基層底最大拉應力值增大，特別是達到1 600MPa時，基層底拉應力增大很快；增大土基彈性模量，面層底和基層底最大拉應力均減小．由此可以總結為路面結構中任一層結構材料彈性模量增加，本層及上層底最大拉應力值會增大，其余層底拉應力隨之減小．增加土基的彈性模量是減小路表最大彎沉值最有效的措施，同時各層的最大拉應力均有所降低，考慮到土基加固處理的經濟費用問題，在土基上部適當的加固以提高土基模量對于提高道路的整體壽命是非常有必要的；同樣的基層材料模量也需要控制在一定范圍內，不能太高也不能太低．

表5 彈性模量取值Tab．5 Elastic Modulus

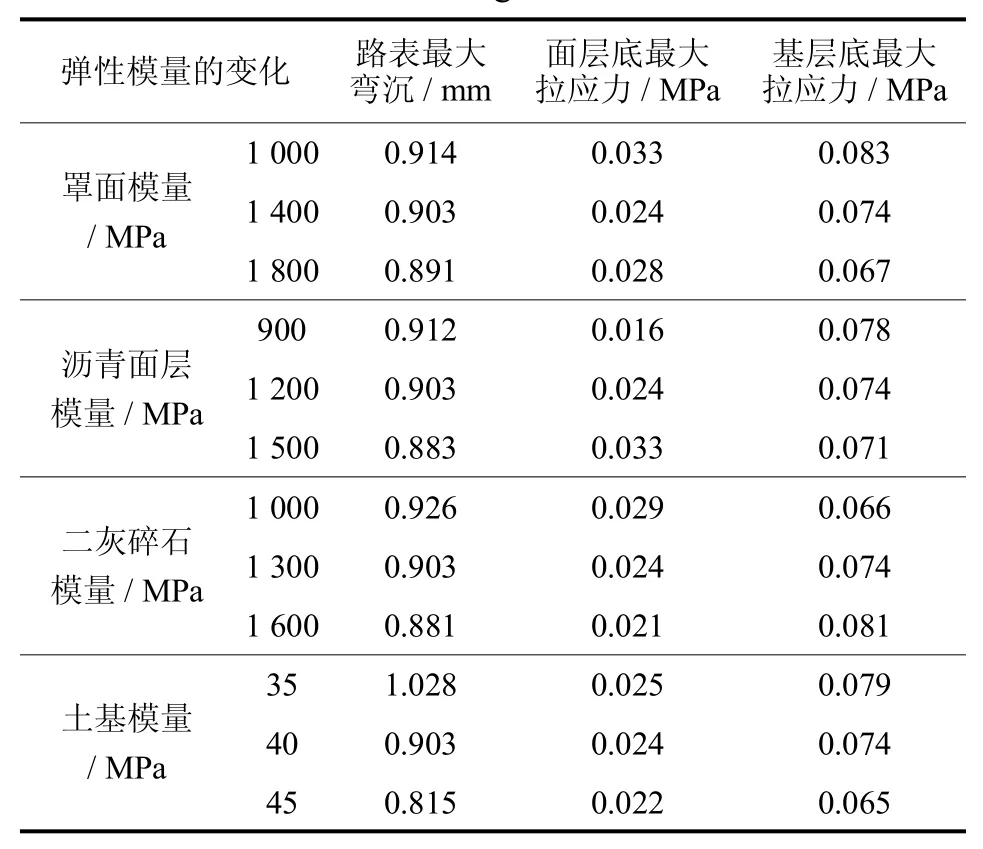
表6 模量改變引起的變化Tab．6 Changes inmodulus

3.3 各結構層泊松比變化分析

同一結構層選用不同泊松比的材料，對動荷載作用下的路面結構響應會有一定的影響，因此需要對各結構層泊松比變化進行分析．對表2路面結構材料參數中各結構層泊松比依次進行改變，每次都只改變一層的泊松比值，其他層泊松比和其他材料參數保持不變，且每層結構按照大到小原則改變3種泊松比，具體的泊松比設置參照表7所示，然后分別計算各結構層取不同泊松比時的路表最大彎沉和面層、基層底最大拉應力值的變化，如表8所示．

表7 泊松比取值Tab．7 Poisson's value

通過表8可以看到各結構層材料的泊松比變化都會對路表最大彎沉值產生影響，但影響的規律和幅度不一樣：罩面、面層和土基材料泊松比的增加可以減小路表最大彎沉值，尤其是土基泊松比的增加對最大彎沉值影響顯著；相反的增加基層材料泊松比會使路表最大彎沉小幅度增大．

對于層底最大拉應力，增加罩面材料泊松比，面層底和基層底最大拉應力都有相應的減小；增加瀝青面層泊松比，面層底最大拉應力有所增加，而基層底最大拉應力變化不大；增加基層材料泊松比，面層底和基層底的最大拉應力都隨之增加，且基層底拉應力增加幅度較大；增加土基泊松比，面層底拉應力增加，基層底最大拉應力減小，且減小幅度較大．由此可見基層材料泊松比不宜過大，否則會導致面層底和基層底拉應力過大，在設計時要嚴加控制[8-9]．

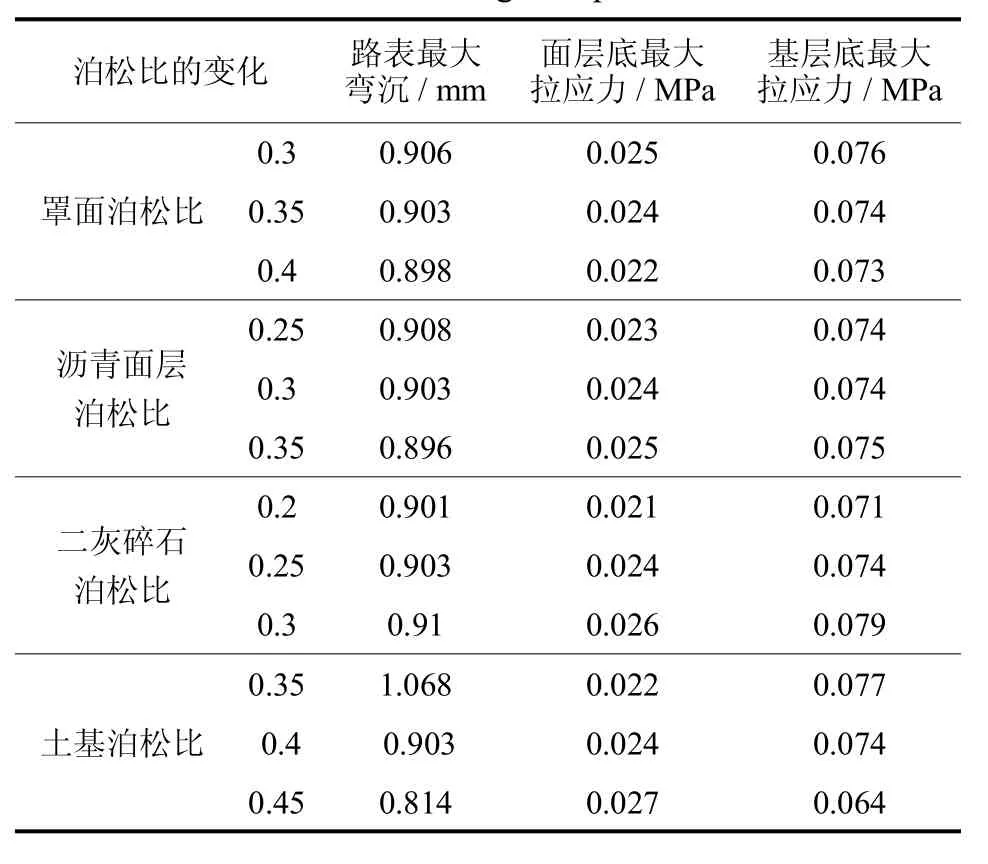
表8 泊松比改變引起的變化Tab．8 Changes in poisons

4 結論

1）不同行車速度下，路表彎沉值表現不一，整體來說處于高速時路表彎沉值較小且變化平穩；不平整度對路表彎沉影響較大，隨著不平整度值的增大，彎沉值大幅增加，所以保持路面平順是避免道路過大彎沉量的必要措施．

2）隨著行車速度的提高，層底拉應力保持平穩的減小趨勢；與路表彎沉一樣，不平整度對層底拉應力的影響也很顯著，隨著不平整度值的增大，基層底拉應力顯著增大，增幅達到66.6%，所以保持路面平順對于減小道路層底拉應力也至關重要，需要高度重視．

3）通過路面結構參數的變化對道路力學分析可以得到：增加各層厚度都可以有效減少路表最大彎沉和層底最大拉應力值，尤其是基層材料厚度的增加效果比較顯著，且從經濟效益方面考慮，適當增加基層厚度比增加面層厚度更加經濟有利；增加各層材料的彈性模量都可不同程度的減小路表最大彎沉，但對層底拉應力的影響比較復雜，綜合考慮通過提高土基模量來減少路表彎沉和層底最大拉應力是最有效的措施，其次適當提高基層材料模量也可以提升道路整體承載抗變形能力；泊松比對道路力學影響比較明顯，除了基層材料泊松比會增加路表彎沉外，罩面、面層和土基泊松比的提高都會減少路表彎沉，而且增加基層泊松比還會導致面層底和基層底最大拉應力的增大，綜合之后得到結論土基泊松比可以適當提高，對減少路表彎沉和層底拉應力有利，相反要控制基層材料泊松比，防止造成過大層底拉應力和路表彎沉量．

[1]鄧學鈞，張登良．路基路面工程 [M]．北京：人民交通出版社，2004．

[2]鄧學鈞，孫璐．車輛-地面結構系統動力學 [M]．北京：人民交通出版社，2000．

[3]蘭輝萍，李德建．高速公路路基的動力響應分析 [J]．西部探礦工程，2003，15（8）：160-162．

[4]向坤山．動載作用下半剛性路面動力響應的三維有限元模擬 [J]．湖南交通科技，2006，32（3）：53-55．

[5]周長峰，孫蓓蓓，孫慶鴻．鉸接式自卸車懸架系統動力學建模與仿真 [J]．汽車技術，2004，35（9）：15-18．

[6]黃雪嬌，曹源文，李仕峰．基于ADAMS重型半掛車動荷載仿真分析 [J]．重慶交通大學學報（自然科學版），2012，31（1）：128-132．

[7]廖公云，黃曉明．ABAQUS有限元軟件在道路工程中的應用 [M]．南京：東南大學出版社，2008．

[8]單景松，黃曉明，廖公云．移動荷載下路面結構應力響應分析 [J]．公路交通科技，2007，24（1）：10-13．

[9]JTGD50-2006，公路瀝青路面設計規范 [S]．北京：人民交通出版社，2006．

[責任編輯 楊 屹]

Pavementstructuralmechanicsbased on the dynamic load simulation

HOU Jing

(Schoolof Civil Engineering,Tianjin Chengjian University,Tianjin 300384,China)

Forpavementresponseand impactanalysisof theproblem under trucksdynam ic load,the corresponding threedimensionalmodelof the pavementstructureand dynam ic loads dynamic simulationmodel with theapplication of ABAQUS finite elementsoftwarewere established.The reliability ofmodelwas verified through the field test;the deflection and layersstress situationsof the roadwascalculated;and parameterson themechanical response of pavementstructure wasanalyzed;The speed,flatness,and road load parameterson pavement responseswere studied so that itcan provide a theoreticalguidance for the pavementdesign and road constructionmaintenance.

dynamic load;flatness;dynam ic simulation;finite element

U416.217

A

1007-2373(2016)01-0114-05

10.14081/j.cnki.hgdxb.2016.01.021

2015-07-06

河北省科技計劃項目（12217636）

侯靜（1976-），女（漢族），講師．