空間向量解立體幾何中的位置關系

江蘇省如皋市搬經中學 王正勇

空間向量解立體幾何中的位置關系

江蘇省如皋市搬經中學 王正勇

立體幾何問題是歷年來高考必考的內容，求立體幾何中的位置關系也成為了重要考點，空間向量的引入使其變成解決立體幾何問題的一項非常重要的工具。其在解決此類問題時體現出的實用性、靈活性、簡便性是其他方法不能實現的，很大程度地降低了立體幾何問題的難度。

立體幾何；位置關系；空間向量

利用空間向量表示空間中的點、線、面，使空間立體問題轉化為向量問題，進而實現代數運算，完成了由難化易的轉換。本文中通過實例列舉出不同情況下空間向量的運用，希望可以幫助學生走出這一難點，更好地應對立體幾何中的位置關系。

一、空間向量解位置關系所用的解題方法介紹

在介紹空間向量在立體幾何中證明位置關系的方法之前，我先列出在解題過程中要用到的空間向量求法以及解題策略，以便在后續的題目解答中學生會有更加清晰的解題思路，避免出現學生難以理解的知識，讓學生學習得更加透徹。

（1）空間直角坐標系的建立：對空間直角坐標系最基本的要求就是遵從右手法則。建立的原則應是保證相關點盡可能簡便地寫出其坐標或者利于后續點坐標的求解。

（2）法向量的計算：建立適當的平面直角坐標系后，假設平面的法向量為，再在所求平面內找出兩條相交的直線，由于垂直于平面的向量必垂直于平面內的直線，利用垂直向量點乘為零列出方程組，然后假設三個未知數中的一個為特殊值，從而求出另外兩個未知數的值。

（3）向量法證明垂直：證明線面垂直時，通常證明直線所在向量平行于平面的法向量，即（p為常數）；證明面面垂直時，通常證明兩平面的法向量是互相垂直的，即。

以上幾種方法的介紹基本包括了位置關系的全部知識。學生應注意的是，雖然在解決空間位置關系時常用向量法，但此種方法并非是最優選擇，有時傳統方法證明會更加簡潔，向量法也并非可以解決所有立體幾何問題。我們學習數學，就是需要用辯證的眼光看問題，活學活用才是解決數學問題的必勝法寶。

二、空間向量求空間圖形的位置關系

這里重點探究的空間圖形的位置關系為平行與垂直，包括直線與直線、直線與平面、平面與平面之間的平行和垂直問題。引入空間向量之后，利用直線的方向向量和平面的法向量，只需簡單的運算，即可證明此類問題。

例1 如圖，幾何體P-ABCD是底面為正方形的四棱錐，側棱PD⊥底面ABCD，PD=DC，E為PC中點，F為PB上一點，且EF⊥PB。求證：（1）PA∥平面EDB；（2）PB⊥平面EFD。

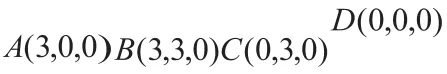
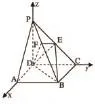
點撥：本題中提到的是線面關系，法向量的求法已經給出，所以本題中就省略了此過程。在解決其他的情況時，我們可以利用線線問題、線面問題、面面問題的相互轉化，提升自身的空間想象力，開拓思維，探索出新的解題方法。

三、空間向量解決探索性位置問題

探索性問題一般就是存在動點，使點所在直線或者平面滿足空間上的位置關系或數量關系。此類問題可以最直接最完美地體現空間向量的優點，位置的不確定性可以通過坐標來表示，這就給我們解決此類問題提供了良好的理論基礎。

例2 如圖，P-ABCD是底面為矩形的四棱錐，PA垂直于底面ABCD，E為PD中 點。BC=1，，PA=2。（1）求直線AC與PB所成角的余弦值；（2）N為平面PAB內一動點，是否存在點N，使NE垂直于平面PAC?

解析：由于N點位置的不確定，故坐標也是不確定的。N點在平面PAB上，所以點N的y坐標為0。建立如圖所示的空間直角坐標系，則可得到如下點的坐標：

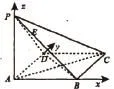
（1）根據各點坐標即可求出答案，故略。

點撥：假設出N點的坐標是本題中的重點。在此類問題中不同于以往的列式求解，通過坐標的代入完成了由空間幾何圖形到代數問題的轉換，在降低了維數的同時又很大程度地減少了計算量，將探索性問題化難為易，實現以靜制動。

以空間向量作為解決立體幾何的工具，真正地實現了數與形的完美結合，在高中數學中應用此方法可以一定程度上解決學生在空間想象能力上的缺陷，在有效的描述圖形中多種數量關系以及位置關系的同時，極大地降低了立體幾何問題的難度。