雙調諧液體柱形阻尼器及其基本動力性能*

閆維明， 倪 銘， 王 瑾

(北京工業大學工程抗震與結構診治北京市重點試驗室 北京, 100124)

?

雙調諧液體柱形阻尼器及其基本動力性能*

閆維明， 倪 銘， 王 瑾

(北京工業大學工程抗震與結構診治北京市重點試驗室 北京, 100124)

借鑒被動調諧質量阻尼器(tuned mass damper,簡稱TMD)和調諧液體柱形阻尼器(tuned liquid column damper, 簡稱TLCD)各自的優缺點，結合土木工程結構減震裝置的經濟性和適用性，提出了一種雙調諧液體柱形阻尼器(doubly tuned liquid column damper,簡稱DTLCD)，建立了簡諧激勵作用下單自由度DTLCD控制體系(DTLCD-SDOF)的運動方程，推導了其動力反應放大系數。提出了針對DTLCD的調優策略及優化評價函數，通過相關算法獲得DTLCD-SDOF系統的參數優化程序，并利用該程序得到了DTLCD的最優參數。具體分析了不同參數對DTLCD共振峰值和調頻寬度的影響，并對阻尼器阻尼參數或受控結構頻率發生變化后DTLCD的魯棒性進行了評價。對DTLCD, TMD, TLCD及DTMD的有效性和魯棒性進行了對比分析。理論與數值研究結果表明，DTLCD的控制效果明顯優于TMD和TLCD，與DTMD效果相同，并且在主結構頻率的攝動方面擁有更佳的魯棒性。事實證明，DTMD比TMD和TLCD更具工程適用性。

雙調諧液體柱形阻尼器；雙調諧質量阻尼器；優化設計；簡諧激勵；有效性；魯棒性；振動控制

引 言

自從1909年Frahm提出TMD后，利用吸振器控制結構振動成為了一種常用的減振手段[1]。許多學者在TMD的基礎上提出了很多不同類型的被動吸振器，包括多重調諧質量阻尼器(multiple tuned mass damper，簡稱MTMD)、調諧液體阻尼器(tuned liquid damper，簡稱TLD)以及TLCD。由于被動吸振器能夠有效地減低結構受到地震或風荷載所引起的反應，因此已有很多吸振器被安裝在了各地的高聳建筑上，如美國紐約的Citicorp Center、波士頓的John Hancock Building及澳大利亞的悉尼塔等[2]。此后，眾多學者對各類被動吸振器進行了詳細的研究[3-17]。結果表明， TLCD雖然能夠有效地降低結構的振動，但由于TLCD本身構造的限制，其控制效果不如TMD和TLD，且控制效果和魯棒性遠不如MTMD。但由于TLCD的水箱本身能夠提供阻尼，其構造比MTMD更簡單。結合TLCD和MTMD的特性，筆者提出一種DTLCD及其數值優化策略與方法，對參數影響分析、有效性和魯棒性進行系統地研究，并對DTLCD，TLCD，TMD和DTMD的有效性和魯棒性的優劣進行對比分析。

1 DTLCD理論模型及動力方程推導

DTLCD是在傳統的TLCD與主結構之間設置彈簧和阻尼的新型液體柱形阻尼器，由設置在主結構上的U形水箱以及連接水箱與主結構的滑動裝置、彈簧和阻尼器構成。當主結構為單自由度時，DTLCD與主結構的理論模型如圖 1所示。主結構的質量、剛度和阻尼分別為m0,k0和c0；DTLCD的質量、剛度和阻尼分別為m，k1和c1；DTLCD的寬度為b，水流運動方向總長度為L；U形水箱截面積為A；x0，x1和x2分別為主結構位移、水箱位移和水沿水流方向位移；地面加速度為ag。

由圖 1的理論模型，可以建立主結構的動力方程為

(1)

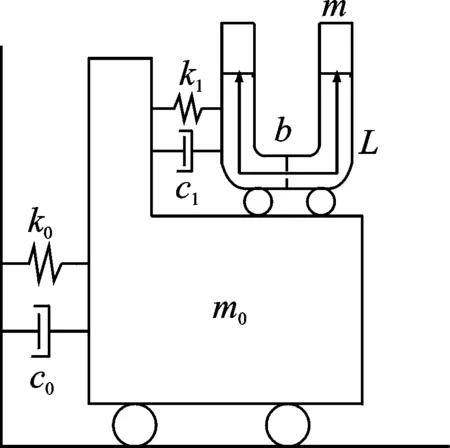
圖1 單自由度結構DTLCD模型示意圖Fig.1 DTLCD-single-degree-of-freedom system

水流的力平衡方程為

(2)

水箱與主結構的相互作用力平衡

(3)

聯立式(1)、式(2)和式(3)得

(4)

其中：m1=ρAb；m2=ρAL；k2=2ρAg 。

對式(4)做Laplace變換可得

(5)

為了將式(5)進行化簡，引入無量綱化參數質量比、頻率比和阻尼比，各參數表示如下

將上述無量綱參數代入式(5)整理后得

(6)

整理式(6)得

(7)

其中

解式(7)得到結構與子質量的傳遞函數為

結構位移放大系數為

(8)

式(8)即為DTLCD控制下單自由度結構的動力放大系數。

2 DTLCD調優策略及優化評價函數

傳統TLCD與TMD的調優策略無異，會因主結構阻尼的有無而不同：當主結構不存在阻尼時，無論TLCD本身是否設置阻尼，TLCD的最優參數均可利用定點理論得到，具體方法是將動力放大系數(DMF)-γ圖中的定點高度保持一致，并使之成為曲線上的極大值點；而當主結構有阻尼時，定點理論不再適用，這時只能利用數值方法通過優化函數尋找TLCD的最優參數。常用的優化函數[2]為

Z=min{max[DMF]}

(9)

對于TLCD，要先找出不同的頻率比和阻尼比下的DMF最大值，再從中找到最小的一個，其對應的參數即是最優參數。需要指出的是，這種針對TLCD的調優策略卻不宜用在DTLCD上。因為TLCD的尋優對象只有U形水箱的阻尼比和頻率比，但DTLCD中卻有相對質量比μ′( 水流總長度L與水平段長度b的比值)、各自的阻尼比(ζ1和ζ2)以及頻率比(λ1和λ2)，共5個尋優對象，利用上面的優化函數難于實現調優。因此，針對DTLCD多參數的特點，筆者提出了一種基于峰值的調優策略和優化函數。

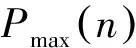
(10)

(11)

(12)

其中：式(10)為使各峰值之間相差最小的優化評價函數；式(11)為使各峰值的均值最小的優化評價函數；式(12)中的P值為兩函數之和，當且僅當P1和P2均為最小值時，即P為最小值時，此時DTLCD的各參數為最優參數。

對于DTLCD-SDOF(單自由度，single degree of freedom,簡稱SDOF)系統，其位移放大系數響應曲線具有3個共振峰值，即n=3。

利用這個優化評價函數，筆者通過Matlab軟件編寫了DTLCD系統的參數優化程序，并利用該程序探索得到了DTLCD的最優參數。

3 DTLCD基本參數分析

3.1 DTLCD調優分析前提及最優參數

不失一般性，在利用程序尋找DTLCD最優參數之前，給定結構阻尼比ζ0=0.02，DTLCD總質量比μ=0.05，定義m1和m2的相對質量比μ′=μ2/μ1(即寬高比L/b)。綜合考慮分析耗時和優化參數的實際可操作性，對參數尋優的范圍進行了限制，阻尼比的范圍限制在0～0.3之間。

在以上的分析前提下，利用程序探索得到了DTLCD的全局最優參數μ′=2.82,ζ1=0,ζ2=0.26,λ1=1.6,λ2=0.89。

下面具體各參數的分析將以此全局最優參數為參照點，比較某個參數固定后得到的條件最優參數。全局最優參數是全部參數(μ′，ζ1，ζ2，λ1和λ2)都參與搜尋后得到的最優參數，與之相對應，條件最優參數則是固定某個參數后搜尋到的最優參數，所以條件最優參數可能和全局最優參數下得到的某些結論相沖突，但并不是說條件最優參數就沒有意義，它可以描述某個參數對于DTLCD系統的影響。

3.2 水箱的阻尼比ζ1

在待優化的5個參數中，下層TLCD的阻尼比ζ1有其獨特的作用和特征，對DTLCD的有效性有較大的影響。圖 2給出了不同阻尼比和質量比下主結構DMF最大值隨ζ1變化的趨勢。

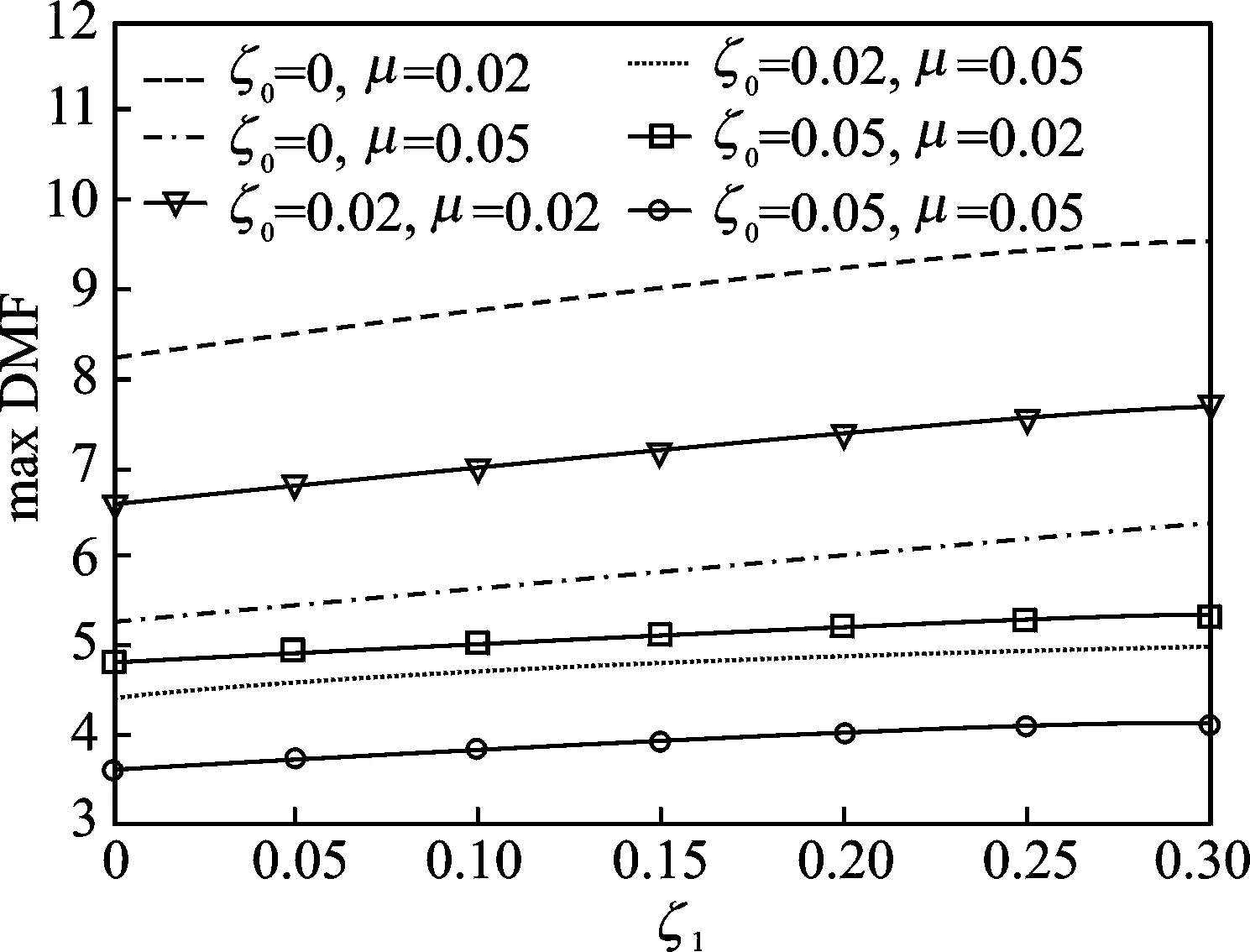
圖2 ζ1變化趨勢圖Fig.2 Trends of ζ1

由圖 2可知，DTLCD在主結構阻尼比分別為0，0.02，0.05和吸振器總質量比分別為0.02，0.05時，最大的DMF峰值都隨著ζ1的增大而單調增大，即最大的DMF峰值在ζ1=0時取值最小，主結構的動力反應最小。6條曲線相同的單調性證明，對于不同阻尼比的受控結構和不同質量比的DTLCD，ζ1的影響是一致的。

另外，由圖 2中的6條曲線可知，在主結構阻尼比和吸振器總質量比分別相同時，主結構阻尼比對最大DMF峰值的影響更大，相比質量比增大對最大DMF峰值的降低，其效果更加明顯。但這是吸振器設計中的不可控因素，增大吸振器總質量比能夠接近于主結構阻尼比增大的效果，這是設計中可以做到的。

總之 ，無論主結構阻尼比和DTLCD總質量比取何值，DTLCD系統ζ1的全局最優參數均為零，而吸振器總質量比增加后其減振效果不如主結構阻尼比的增加，這兩個規律與雙重調諧質量阻尼器(doubly tuned mass damper,簡稱DTMD)是極為一致的，而在TLCD上則沒有體現。

3.3 水流的阻尼比ζ2

ζ2對DTLCD系統的影響見表 1。表 1中均為固定ζ2后程序找到的條件最優參數，其中第6行為全局最優參數。

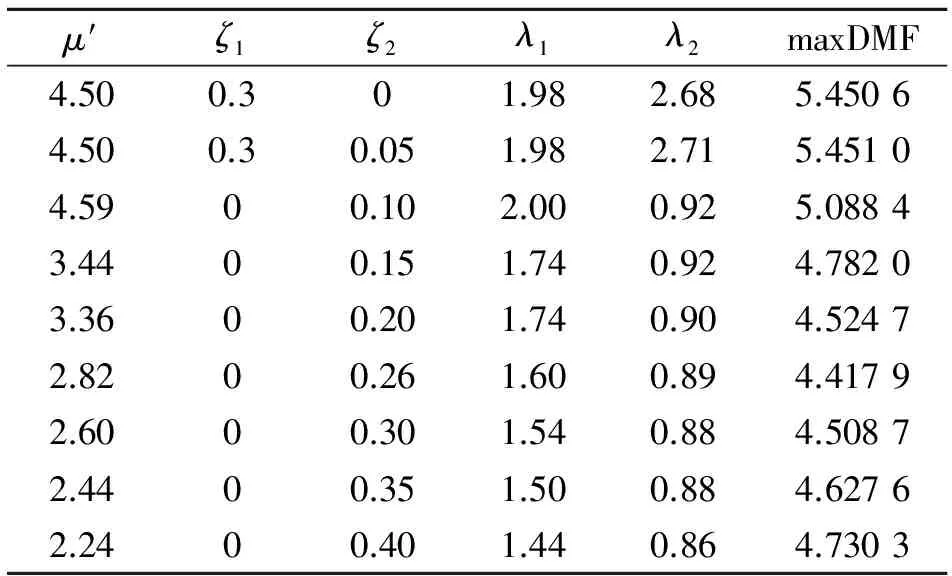
表1 隨ζ2變化的條件最優參數

由表 1可以看到，ζ2以步長0.05由0增加到0.4的過程中，其他參數呈現出一起單調變化的規律。當ζ2分別為0和0.05時，兩者的條件最優參數十分接近，最大DMF峰值也相差不多，可以說明較小的ζ2對DMF的影響都十分接近，也不是全局最優參數的取值范圍。但是在ζ2從0.1增加的0.4的過程中，其他參數則表現出一致的變化規律，μ′ ，λ1和λ2隨之單調遞減，ζ1則一直為0，最大DMF峰值經歷了一個先降低到最小值后增大的過程。

圖 3展示了主結構動力放大系數在不同的ζ2下隨頻率比γ變化的曲線，參數皆取自表 1中的條件最優參數。

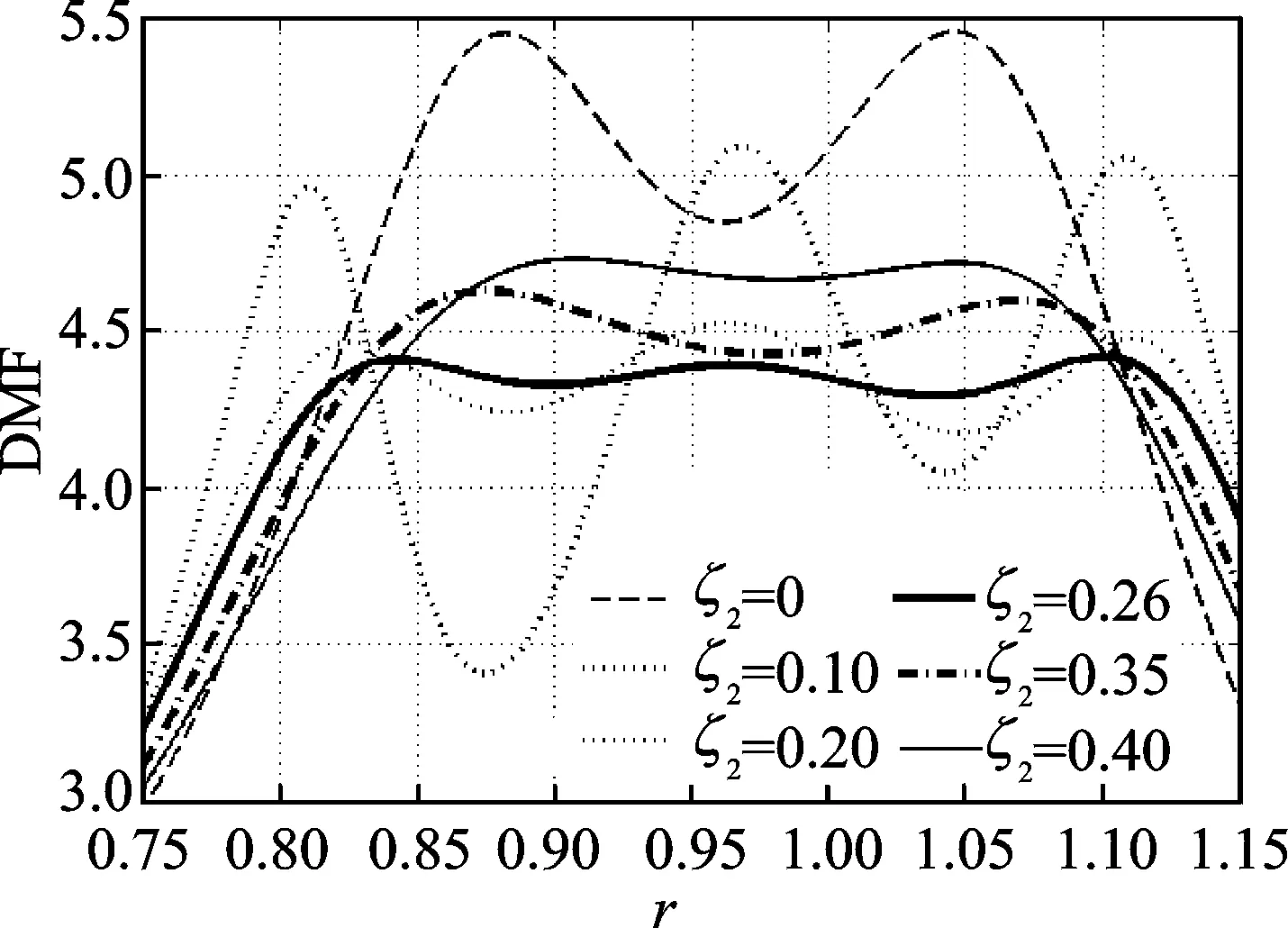
圖3 不同ζ2下的主結構響應曲線Fig.3 Frequency response curves of structure for different ζ2

由圖 3可以看到,在ζ2過大或者過小時(ζ2=0，0.35,0.40),DMF曲線都只有2個峰值，這是因為當阻尼比過大會抑制DTLCD中水流與水箱之間的共振，使其不能很好地耗散主結構的振動能量；ζ2過小使得ζ1又過大，共振和能量耗散也被抑制了。另外，當DMF曲線為兩峰值時其調頻寬度都小于三峰值時的調頻寬度，說明調頻寬度對阻尼比的變化也是比較敏感的。在ζ2增大過程中，當ζ2小于全局最優值時，峰值大幅降低到最小值，峰值對較小的ζ2更敏感；當ζ2大于全局最優值時，峰值緩慢增加，較大的ζ2對峰值影響較小，這是因為較大的阻尼比對總體振動的抑制要優于較小的阻尼比。

總之，當ζ2≤0.1時不同的阻尼比對峰值的影響十分接近，而在ζ2>0.1時其他條件最優參數會隨著ζ2的增大單調變化，過大或是過小的ζ2都無法有效地抑制主結構的共振和能量的耗散，調頻寬度也無法達到最優效果。因此，存在一個最優的ζ2使得DMF峰值最小。

3.4 相對質量比μ′(寬高比L/b)

相對質量比μ′的實質是水流總長度L與水平段長度b的比值，這個比值不能過小，否則會造成U型管豎向長度不足，進而水柱晃動使得豎管中出現完全無水的現象，這將破壞U型水箱中水運動的計算模型，從而達不到設計預定的減振效果。

μ′對DTLCD系統的影響見表 2。表 2中均為固定μ′后程序找到的條件最優參數，由于上面提到的原因，故表中的μ′由2遞增至7，其中第3行為全局最優參數。

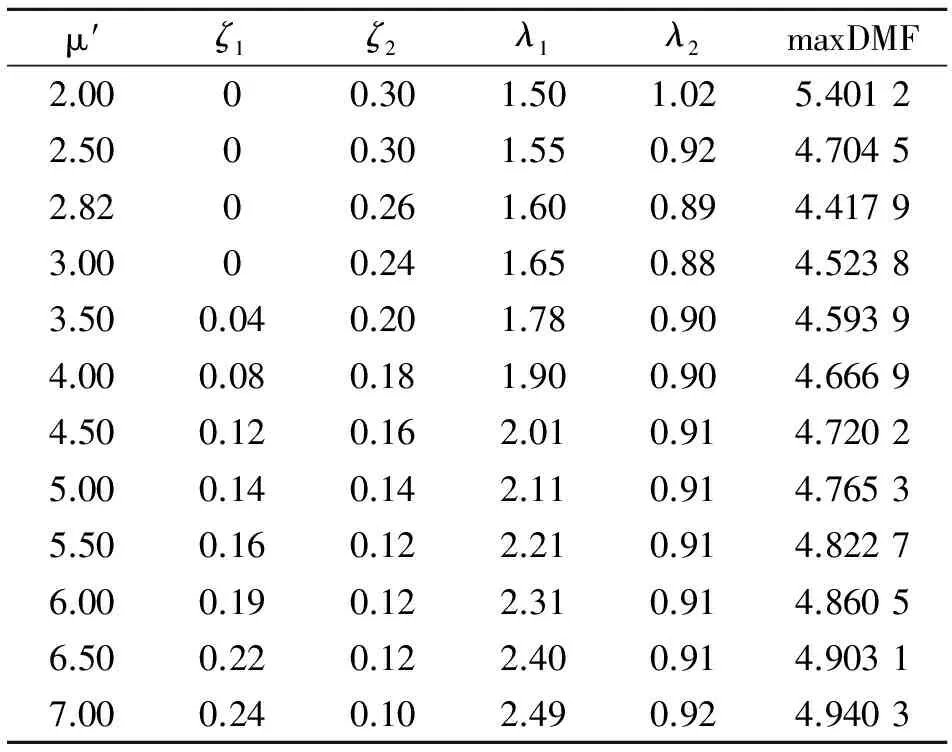
表2 隨μ′變化的條件最優參數表

由表 2可知，μ′自2以步長0.5增加到7的過程中，其他參數隨之單調變化，其中ζ1和λ1是單調遞增，ζ2和λ2是單調遞減，最大DMF峰值則經歷了降低到最小值后再逐步增大的過程。另外，在μ′大于2.5之后，最大DMF值都能很好地控制在5以下，只有μ′=2時為5.401 2，說明對于DTLD來說，過小的相對質量比會對控制效果造成不良影響，這與TLD的規律不同，因為TLD要求寬高比L/b的比值越小越好，而DTLD則要求一個適當的相對質量比。

圖 4給出了主結構的動力放大系數在不同的μ′ 下的變化，參數皆取自表 2中的條件最優參數。

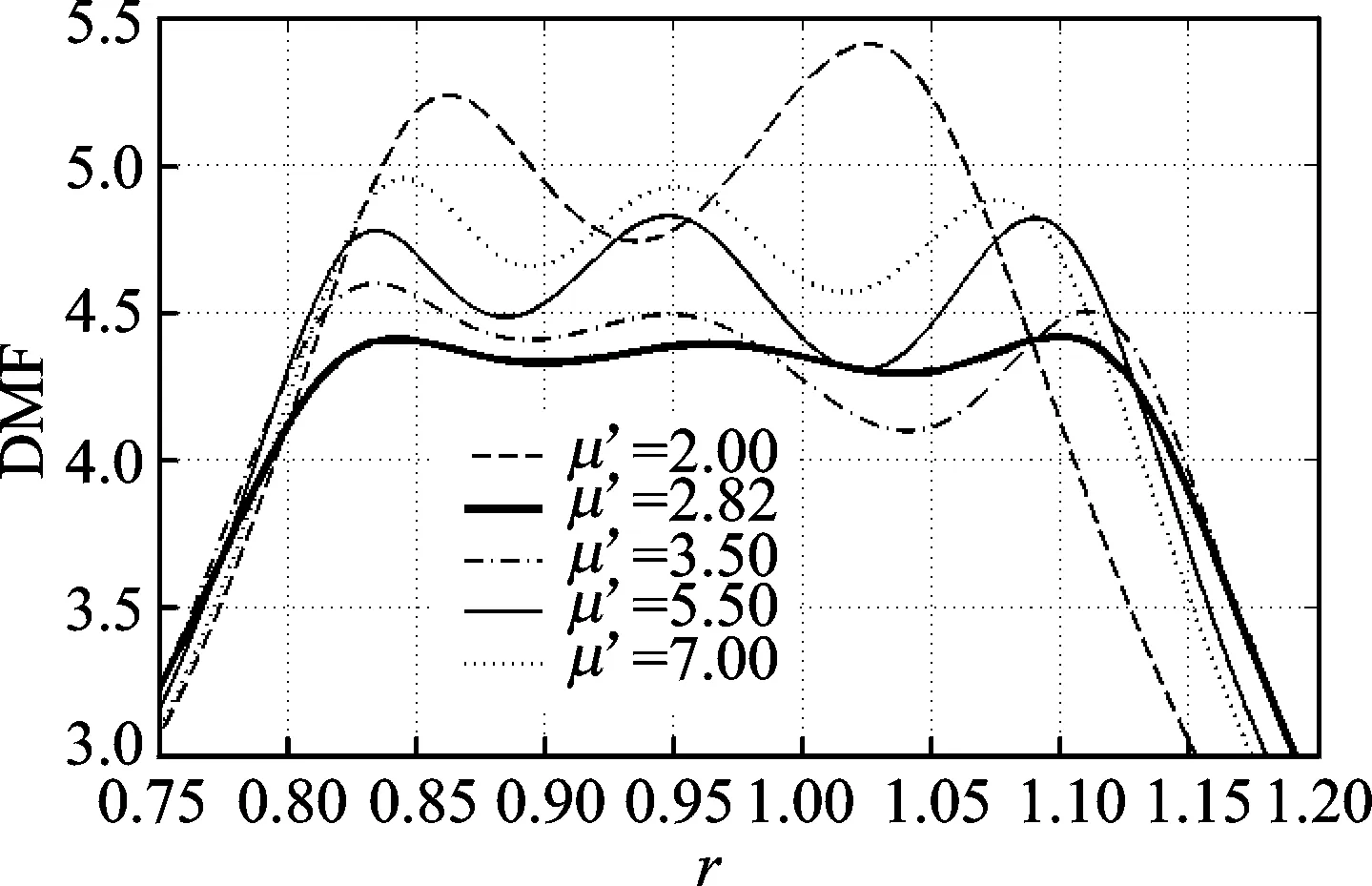
圖4 不同μ′下的主結構響應曲線Fig.4 Frequency response curves of structure for different μ′

由圖 4可知，在μ′由2增加到最優值2.82，再增加到7的過程中，當μ′小于最優值時峰值下降速度很快；但μ′大于最優值時，峰值的增長則相對緩慢。另外，在μ′=2時，DMF曲線值有2個峰值，說明μ′偏小時不利于水流與U型管之間的共振，造成無法有效耗散主結構的振動能量，控制效果變差。而當μ′=3.5時，DTLCD的控制效果相對全局最優參數來說增大的并不多，其調配寬度甚至還大一點，這說明在某些特殊的情況下，比全局最優參數稍大一點的相對質量比仍然能夠很好地控制主結構振動。

總之，與TLCD中寬高比L/b越小越好不同，DTLCD需要一個適當的相對質量比使得DMF峰值最小，且過小的相對質量比會使得DTLCD的控制效果大大降低。

4 DTLCD魯棒性分析

4.1 DTLCD阻尼系數的變動

TLCD系統中的阻尼通常取決于管道中不同開洞率的隔板以及不同密度的液體，不同密度的液體在通過開洞率不同的隔板時會產生不同的阻尼。但是，灌注液體密度容易發生變化，導致TLCD系統提供的阻尼比發生變化。因此，筆者以全局最優參數為基準等倍變化，比較DTLCD阻尼系數變動后的控制效果。由于阻尼系數與阻尼比成正比，所以文中直接以無量綱化參數阻尼比為研究對象。另外，全局最優參數中TLCD與主結構之間的阻尼比為0，因此可以不設置阻尼器，故阻尼比的變動只涉及到U型管本身的阻尼比ζ2變化。

由圖 5可知，以全局最優參數為基準，阻尼比在0.6～1.8倍范圍內，DTLCD的控制效果仍然維持在較優的水平，主結構的反應也沒有被過度放大。對于0.2ζ2與3.0ζ2，后者明顯控制效果好于前者，說明DTLCD在阻尼系數變動方面的魯棒性上，對阻尼系數降低更為敏感，控制效果也由此變得較差，而對阻尼系數的變大則能維持在可接受的范圍。

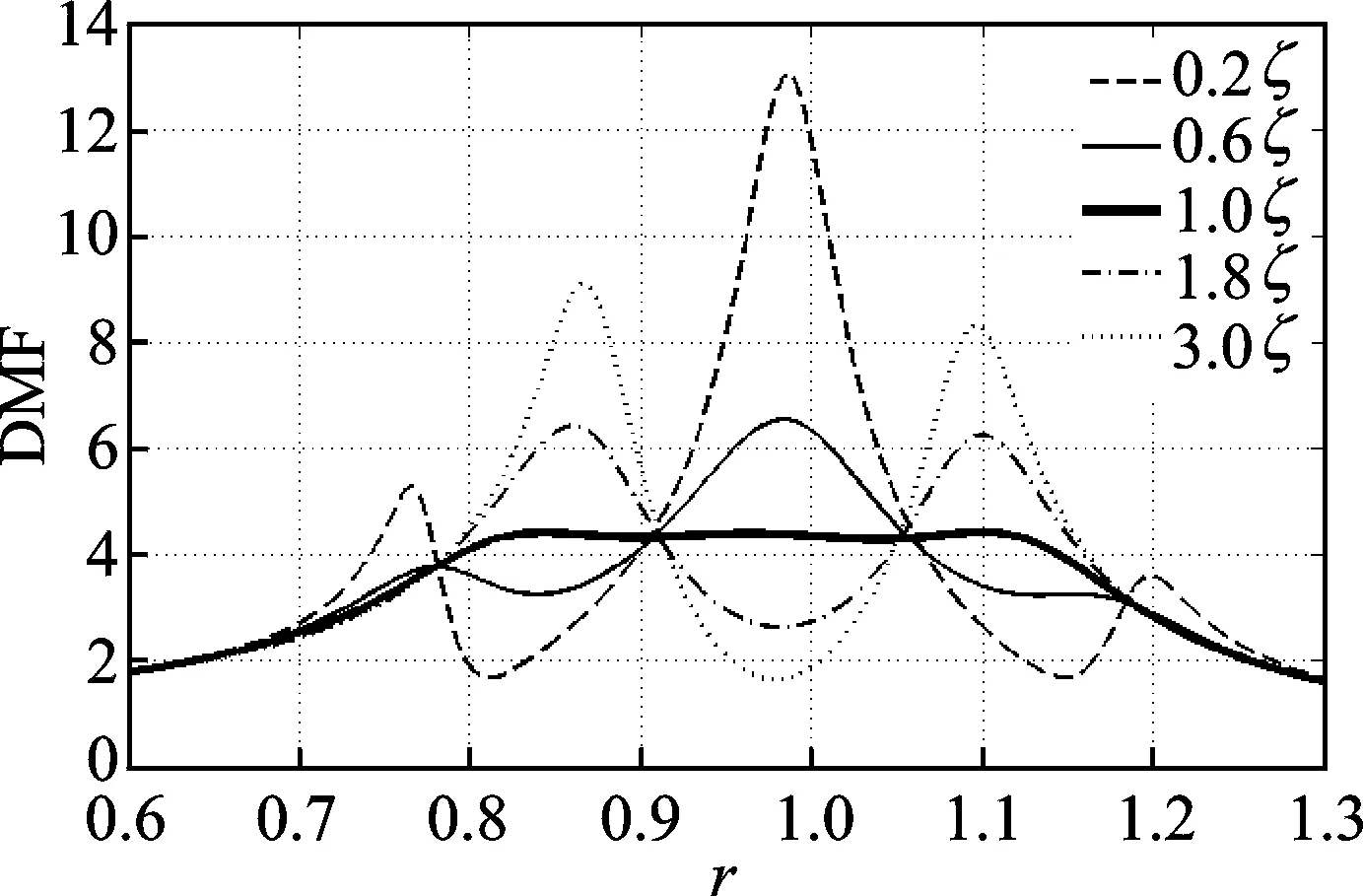
圖5 阻尼比變動情況下的主結構響應曲線Fig.5 Frequency response curves of structure for different damping ratio of DTLCD

4.2 主結構頻率的變動

傳統TMD魯棒性差主要體現在兩點，調頻寬度小以及對主結構參數變化十分敏感。由于TLCD的原理與TMD一致，所以TLCD也有同樣的魯棒性問題。DTLCD系統在TLCD與主結構之間加入彈簧后，形成雙調諧的效果，其固有頻率在主結構的共振峰值附近分散開來，因此即使主結構頻率發生改變，DTLCD仍能發揮作用，從而緩解因固有頻率變動帶來的控制效果的降低。一般來說，固有頻率的變化相當于剛度的變化，圖6為主結構剛度成倍變化后的DTMD的控制效果。

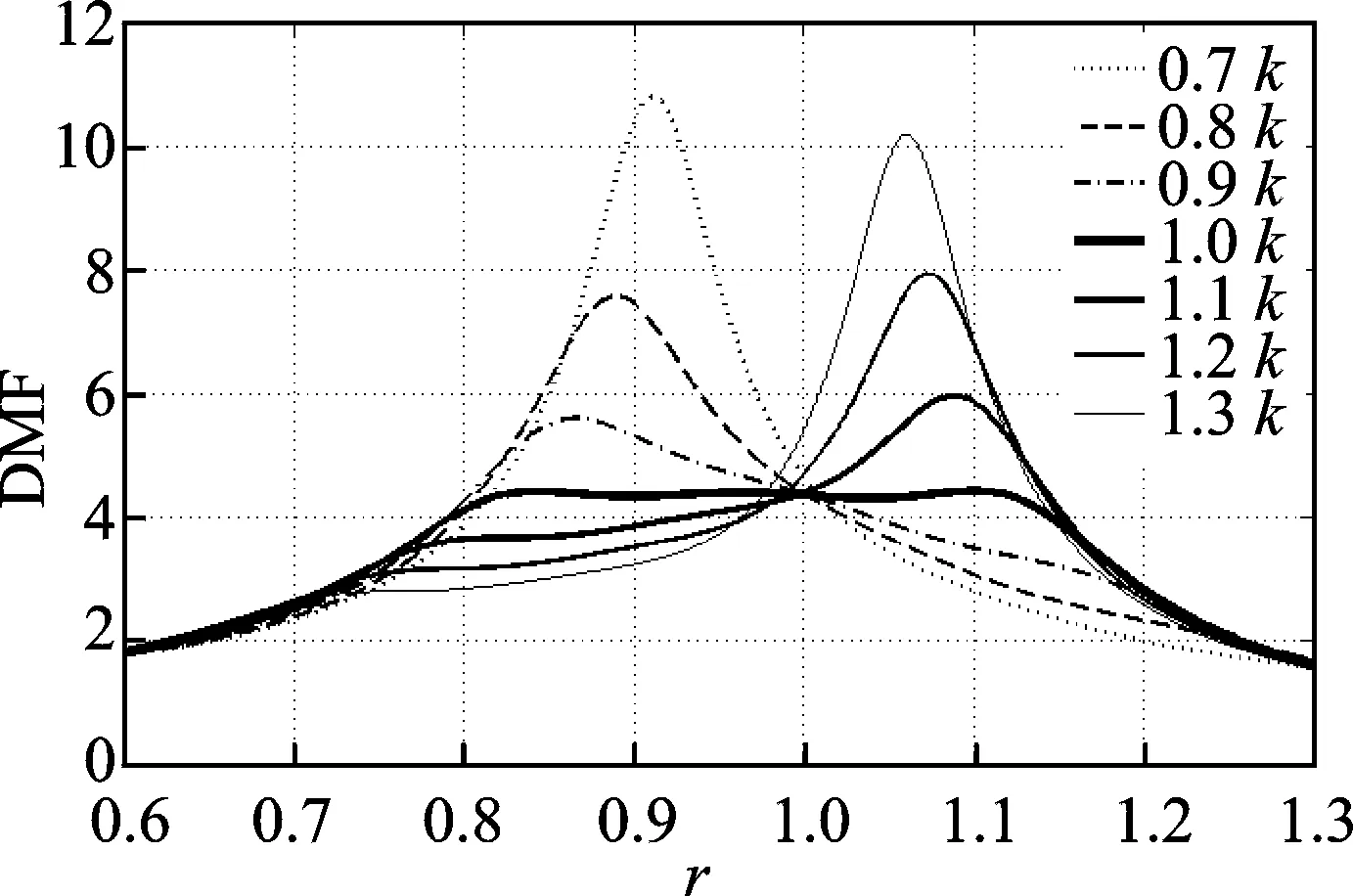
圖6 主結構剛度變化后的響應曲線Fig.6 Frequency response curves of structure for different stiffness

由圖 6可知，以原剛度為基準的DMF曲線，在剛度衰減時峰值偏向左側，在剛度增大時峰值偏向右側，這與DTMD的規律是一致的，與MTMD相反。但無論剛度是衰減還是增大，都經歷了由三峰逐漸變為單峰、峰值增加、調頻寬度減小的過程，這個過程與眾多吸振器是一致的。

5 DTLCD與TLCD的性能比較

本節將對不同吸振器的有效性及魯棒性進行比較。比較對象中各吸振器的主結構與前面DTLCD主結構的基本動力特性相同。各吸振器的參數均為程序探索得到的全局最優參數，其中TLCD的參數如下：質量比為0.05；阻尼比為0.13；頻率比為1.04；相對質量比為1.214。TMD的參數如下：質量比為0.05；阻尼比為0.14；頻率比為0.963 5。DTMD為雙調諧質量阻尼器，即主結構上有2個串聯的質量塊，其參數如下：相對質量比為0.13；阻尼比為0和0.24；頻率比為1.01和0.89。圖7是4種吸振器與原結構的控制效果比較。

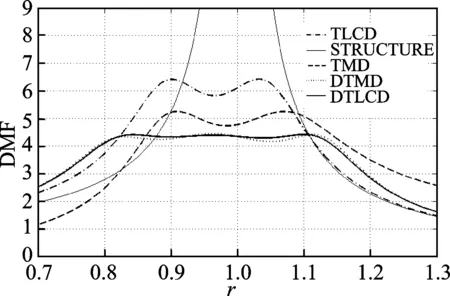
圖7 4種吸振器與原結構的控制效果比較Fig.7 Frequency response curves of structure for four different mass dampers

由圖 7可知，與原結構相比，TMD將主結構的共振峰值降低到了5.2左右，調頻寬度大約為0.16。由于寬高比L/b的限制，TLCD將主結構的共振峰值降低到了6.5左右，調頻寬度大約為0.14，控制效果比TMD要差。DTLCD與DTMD兩者的曲線基本相同，控制效果比TLCD和TMD大大提高，共振峰值為4.4，比TLCD降低32.3%，比TMD降低15.4%，調頻寬度為0.3，比TLCD增大114.3%，比TMD增大87.5%，其控制效果顯著。由此可見，DTLCD和DTMD的共振峰值和調頻寬度基本一致，且曲線基本重合，這是由兩者的理論模型相近造成的?？傊?，雙調諧吸振器的控制效果要優于單調諧吸振器。

對于吸振器，其魯棒性體現在經過最優化調諧后其控制效果在種種變化因素的作用下仍然能夠維持穩定。圖8為主結構動力放大系數最大值隨吸振器中單個TMD阻尼系數變化的曲線，變動的基準均為對應吸振器的全局最優參數，故1.0倍處的動力放大系數最大值最小。

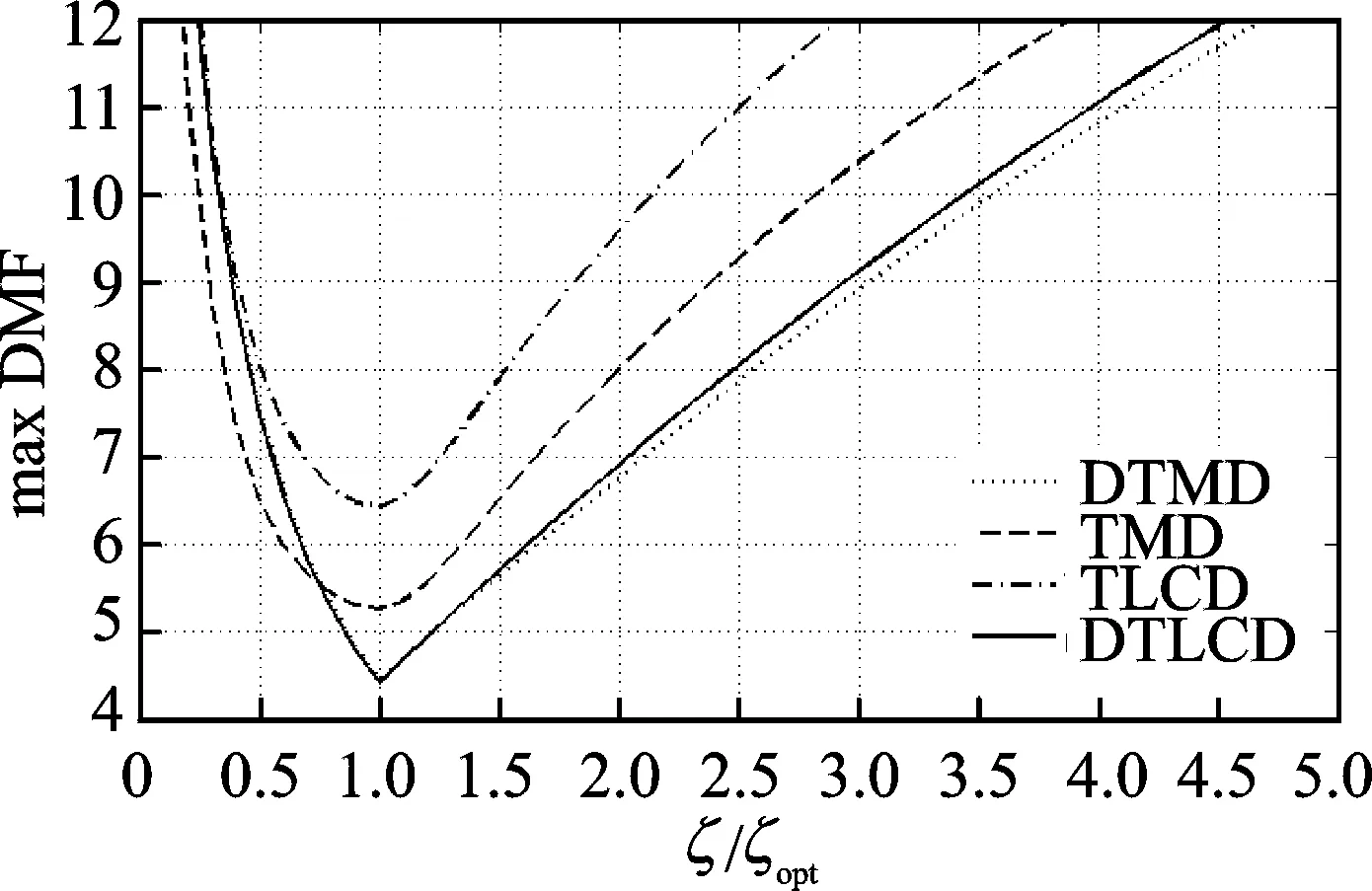
圖8 4種吸振器阻尼系數變化后的比較Fig.8 Frequency response curves of structure change with damping ratio for four different mass dampers

由圖 8可以看出，DTLCD與DTMD的曲線仍然基本一致，只在1.5倍的阻尼系數后比DTMD稍大。相比之下，DTLCD全程都優于TLCD，且在0.75倍阻尼系數后優于TMD。由此可見：在阻尼系數變動方面，DTLCD擁有良好的魯棒性，且與DTMD基本一致；而在阻尼系數過小時，DTLCD對其變動比TMD更加敏感，魯棒性變差，但仍然優于TLCD。因此可以把 DTLCD的阻尼系數設定的比最優值大一些，即使阻尼系數發生變化，動力放大系數最大值的增加也可以得到抑制。

主結構固有頻率的變化也是衡量吸振器魯棒性的重要因素。由于主結構剛度與固有頻率成正比，而且主結構的剛度變化更加直觀，故筆者利用主結構剛度的變化來代替固有頻率的變化。圖9為4種吸振器作用下主結構動力放大系數最大值隨主結構剛度變化的曲線，圖中4種吸振器的參數都是相同基本動力特性下的全局最優參數。

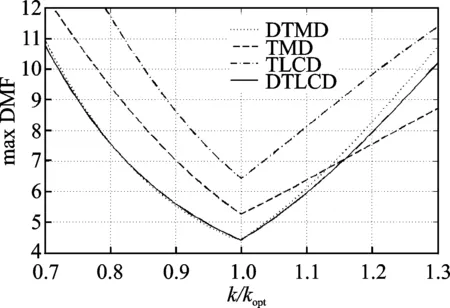
圖9 4種吸振器在主結構剛度變動后的比較Fig.9 Frequency response curves of structure change with stiffness for four different mass dampers

由圖 9可以看出，在剛度減小的區域，DTLCD與DTMD兩者的曲線一致；但在剛度增大的區域，DTMD的動力放大系數最大值逐漸大于DTLCD，說明DTLCD在主結構剛度變化的方面其魯棒性優于DTMD。與剩下的兩者相比，DTLCD在結構剛度變化幅度為-30%～15%內比TMD魯棒性更好，在圖中全程范圍內都優于TLCD?？傊瑢χ鹘Y構頻率的攝動而言，DTLCD的魯棒性對比TMD和TLCD是有較明顯的優勢，而與DTMD相比效果相近，在剛度增大范圍內則略優。

就魯棒性的兩個方面來說，主結構頻率的攝動顯然更為重要，因為阻尼系數是一個可以調節的參數，能通過重新調試或者更換阻尼系數變動的阻尼器來解決。相比之下，主結構頻率本身就存在不便測量和控制的特點，而且一旦主結構頻率發生攝動，工程上也沒有有效的方法可以解決這個問題。因此可以認為，DTLCD的魯棒性比TMD和TLCD更好，與DTMD基本一致。

6 結 論

1) DTLCD系統存在一個最優的相對質量比(寬高比)、阻尼比使得結構的反應最小。其中，無論主結構阻尼比和DTLCD質量比取何值，DTLCD系統ζ1的全局最優參數都是零。

2) 全局最優參數條件下，DTLCD的有效性比TLCD和TMD更優。DTLCD控制下結構的動力反應系數最大值相比TMD和TLCD控制下結構的動力響應分別降低了15.4%和32.3%。DTLCD的調頻寬度比TMD和TLCD分別增大了87.5%和114.3%，對高階振型的控制效果大大增加。DTLCD的控制效果與DTMD基本相同。

3) 當阻尼器的阻尼系數發生攝動時，DTLCD的魯棒性與DTMD相同，在大部分情況下優于TMD，并顯著優于TLCD。在更為重要的主結構固有頻率攝動方面，DTLCD的魯棒性優于TMD和TLCD。

4) 綜合比較DTLCD，TMD和TLCD的有效性、魯棒性和實用性，結果表明DTLCD與DTMD有相同的特性，且更具工程適用性。

[1] Rana R, Soong T T. 調諧質量阻尼器的參數研究與簡化設計[J]. 世界地震工程, 1998, 14(4):91-107.

Rana R, Soong T T. Parametric study and simplified design of tuned mass dampers[J]. World Information on Earthquake Engineering, 1998, 14(4):91-107.(in Chinese)

[2] 背戶一登. 結構振動控制[M].北京:機械工業出版社, 2011:1-40.

[3] Gao H, Kwok K C S. Optimization of tuned liquid column dampers[J]. Engineering Structures, 1997, 19(6):476-486.

[4] 閻石,李宏男,等. 可調頻調液柱型阻尼器振動控制參數研究[J]. 地震工程與工程振動, 1998, 18(4):96-102.

Yan Shi, Li Hongnan, et al. Vibration control parameters research on system with adjusted frequency and tuned liquid column damper [J]. Journal of Earthquake Engineering and Engineering Vibration, 1998, 18(4):96-102.(in Chinese)

[5] Xu Kangming, Igusa T. Dynamic characteristics of multiple substructures with closely spaced frequency [J]. Earthquake Engineering and Structural Dynamics,1992,21:1059-1070.

[6] 李春祥,韓兵康,杜冬，等. 結構雙重調諧質量阻尼器(DTMD)控制策略研究[J]. 土木工程學報, 2005, 38(5):1-9.

Li Chunxiang, Han Bingkang, Du Dong. Control strategy of double tune mass dampers for structures[J]. China Civil Engineering Journal, 2005, 38(5) :1-9.(in Chinese)

[7] 背戶一登. 動力吸振器及其應用[M].任明章，譯.北京:機械工業出版社, 2013:1-50.

[8] Hiroki Y, Napat H. Fundamental characteristics of multiple tuned mass dampers for suppressing harmonically forced oscillations [J]. Earthquake Engineering and Structural Dynamics,1993,22:51-62.

[9] Soong T T, Dargush G F. Passive energy dissipation systems in structural engineering[M]. New York:John Wiley & Sons, 1997:1-25.

[10]翟偉廉，李肇胤,李桂青，等. U形水箱對高層建筑和高聳結構風振控制的試驗和研究[J]. 建筑結構學報,1993, 14(5):37-44.

Zhai Weilian, Li Zhaoyin, Li Guiqing,et al. Experiment and research on control of wind vibration responses of tall buildings and lofty structures by U-shape water tank [J]. Journal of Building Structures,1993, 14(5):37-44.(in Chinese)

[11]閆維明，紀金豹，蔣華戈,等. 新型懸吊式TMD及其在某標志塔風振控制中的應用[J].建筑結構學報,2010, 31(2): 55-60.

Yan Weiming, Ji Jinbao, Jiang Huage. A new type pendulous TMD and its application on a tower for wind-induced vibration control [J]. Journal of Building Structures, 2010, 31(2): 55-60.(in Chinese)

[12]曾勝，任意，程濤濤,等.利用調諧質量阻尼器進行管路系統減振[J].振動、測試與診斷,2012,32(5):823-826.

Zeng Sheng, Ren Yi, Cheng Taotao,et al. Vibration suppression of pipe system with tuned mass damper[J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(5):823-826.(in Chinese)

[13]Tanuja P B, Radhey S J. Dual-layer multiple tuned mass dampers for vibration control of structures[J]. International Journal of Advanced Structural Engineering, 2010, 2(2): 91-113.

[14]Daniel Y, Lavan O, Levy R. Multiple-tuned mass dampers for multimodal control of pedestrian bridges[J]. Journal of Structure Engineering, 2012, 138: 1173-1178.

[15]Clarence W de S. Vibration damping, control, and design [M].LLC, Boca Raton: CRC Press, Taylor & Francis Group, 2007:1-5,6-17.

[16]龍復興,張旭,顧平，等. 調諧質量阻尼器系統控制結構地震反應的若干問題[J]. 地震工程與工程振動, 1996, 16(2):87-94.

Long Fuxing, Zhang Xu, Gu Ping,et al. Problems in seismic responses of structures under the control of tuned mass dampers[J]. Journal of Earthquake Engineering and Engineering Vibration, 1996, 16(2):87-94.(in Chinese)

[17]歐進萍,王永富. 設置TMD、TLD控制系統的高層建筑風振分析與設計方法[J]. 地震工程與工程振動, 1994,14(2):61-75.

Ou Jingping, Wang Yongfu. Wind induced vibration analyses and design methods of tall buildings with tuned mass dampers[J]. Journal of Earthquake Engineering and Engineering Vibration, 1994,14(2):61-75.(in Chinese)

10.16450/j.cnki.issn.1004-6801.2016.06.022

*國家自然科學基金資助項目(51378039; 91315301-03)

2014-09-09；

2014-11-10

TU317+.1; TU352.1

閆維明，男，1960年9月生，研究員。主要研究方向為工程振動與智能控制、結構檢測與健康監控、結構抗震與減震。曾發表《新型懸吊式TMD及其在某標志塔風振控制中的應用》(《建筑結構學報》2010年第31卷第2期)等論文。 E-mail:yanwm@bjut.edu.cn