自適應(yīng)鄰域構(gòu)造流形學(xué)習(xí)算法及故障降維診斷*
張曉濤, 唐力偉, 王 平, 鄧士杰
(軍械工程學(xué)院火炮工程系 石家莊,050003)
?
自適應(yīng)鄰域構(gòu)造流形學(xué)習(xí)算法及故障降維診斷*
張曉濤, 唐力偉, 王 平, 鄧士杰
(軍械工程學(xué)院火炮工程系 石家莊,050003)
針對(duì)流形學(xué)習(xí)算法中近鄰構(gòu)造問題,提出一種自適應(yīng)鄰域構(gòu)造方法,該方法基于馬氏距離計(jì)算樣本間相似系數(shù),由相似系數(shù)均值確定初始近鄰數(shù),根據(jù)樣本高斯核概率密度估計(jì)調(diào)整近鄰數(shù),并將自適應(yīng)鄰域構(gòu)造方法用于改進(jìn)的主成分分析聯(lián)合局部保持投景(principal component analysis-locality preserving projections,簡(jiǎn)稱PCA-LPP)流形學(xué)習(xí)算法中。通過齒輪箱故障類型識(shí)別對(duì)其特征降維性能進(jìn)行驗(yàn)證,結(jié)果表明,自適應(yīng)鄰域PCA-LPP方法比傳統(tǒng)的k近鄰方法及原始無處理的特征識(shí)別率都高,可以達(dá)到94.67%。
自適應(yīng); 鄰域; 高斯核概率估計(jì); 流形學(xué)習(xí); 故障診斷
引 言
流形學(xué)習(xí)算法是一類非常有效的非線性數(shù)據(jù)降維算法[1],在很多具體的流形學(xué)習(xí)算法實(shí)現(xiàn)中,諸如局部保持投影(locality preserving projection, 簡(jiǎn)稱LPP)[2]、拉普拉斯映射(Laplacian eigenmap,簡(jiǎn)稱LE)[3]都需要先構(gòu)造數(shù)據(jù)樣本近鄰圖。傳統(tǒng)的近鄰圖構(gòu)造主要是k近鄰和ε近鄰兩種方法[4],其主要缺點(diǎn)在于各個(gè)樣本的近鄰數(shù)需要人為經(jīng)驗(yàn)確定,且所有樣本采用相同的近鄰數(shù),不能針對(duì)樣本自身的鄰域分布情況進(jìn)行數(shù)據(jù)調(diào)整。自適應(yīng)鄰域的思想主要是基于樣本周圍一定范圍數(shù)據(jù)分布的情況,按照預(yù)設(shè)規(guī)則自動(dòng)確定鄰域大小。目前常用的自適應(yīng)鄰域構(gòu)造思想主要基于歐氏距離或者余弦夾角距離計(jì)算相似系數(shù),并根據(jù)相似系數(shù)的分布設(shè)定閾值自適應(yīng)求取近鄰數(shù),這樣的方法多用于圖像處理及人臉識(shí)別研究中。Yang等[5]基于歐氏距離指數(shù)函數(shù)計(jì)算樣本相似系數(shù)。劉鳳連等[6]基于圖像歐氏距離導(dǎo)數(shù)計(jì)算樣本相似系數(shù)。黃璞等[7]采用樣本夾角余弦距離作為相似系數(shù)。三種方法在人臉識(shí)別研究中取得了良好的分類效果。李城梁等[8]將基于樣本切空間距離的自適應(yīng)鄰域方法應(yīng)用于機(jī)械故障信號(hào)特征提取,故障分類正確率得到明顯提升。
自適應(yīng)鄰域構(gòu)造方法能夠有效避免人為選擇近鄰范圍的隨意性,具有更好的樣本局部非線性流形特征表達(dá)能力。筆者提出一種自適應(yīng)鄰域構(gòu)造方法,基于馬氏距離相似系數(shù)均值及樣本高斯核概率密度估計(jì)調(diào)整自適應(yīng)獲得樣本近鄰數(shù),并將自適應(yīng)鄰域構(gòu)造方法應(yīng)用于PCA-LPP流形學(xué)習(xí)算法,通過齒輪箱故障信號(hào)特征向量降維識(shí)別驗(yàn)證了自適應(yīng)鄰域PCA-LPP方法的有效性。
1 自適應(yīng)鄰域構(gòu)造方法
設(shè)高維空間RD中存在數(shù)據(jù)集X=[x1,x2,…,xN],基于近鄰圖構(gòu)造相似矩陣S能夠用于多種流形學(xué)習(xí)算法,實(shí)現(xiàn)數(shù)據(jù)的降維處理。
傳統(tǒng)的k近鄰構(gòu)造方法,基于樣本間的歐氏距離計(jì)算樣本相似性,每個(gè)樣本近鄰值相同,相似系數(shù)具體表達(dá)如下
(1)
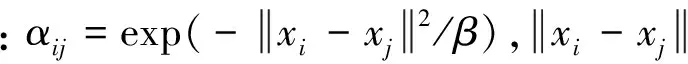
k近鄰法存在兩點(diǎn)不足:a.所有樣本采用相同的近鄰數(shù),不能很好地適應(yīng)每個(gè)樣本的局部流形結(jié)構(gòu)特征;b.近鄰數(shù)的選擇沒有成熟的算法,常使用的交叉驗(yàn)證方法存在效率低下等弊端。
1.1 馬氏距離相似度衡量
馬氏距離是一種基于數(shù)據(jù)協(xié)方差的距離描述,其定義為
(2)
其中:C為數(shù)據(jù)集X的協(xié)方差矩陣。
馬氏距離對(duì)一切非奇異性線性變換具有不變性,不受特征量綱選擇的影響。馬氏距離與歐氏距離的對(duì)比如圖1所示,圖中虛線圓為歐氏距離等距線,實(shí)線橢圓為馬氏距離等距線。由圖1可以看出,馬氏距離的描述更符合數(shù)據(jù)真實(shí)的分布情況,僅當(dāng)協(xié)方差矩陣C為單位矩陣時(shí),馬氏距離與歐氏距離才會(huì)相等[9]。
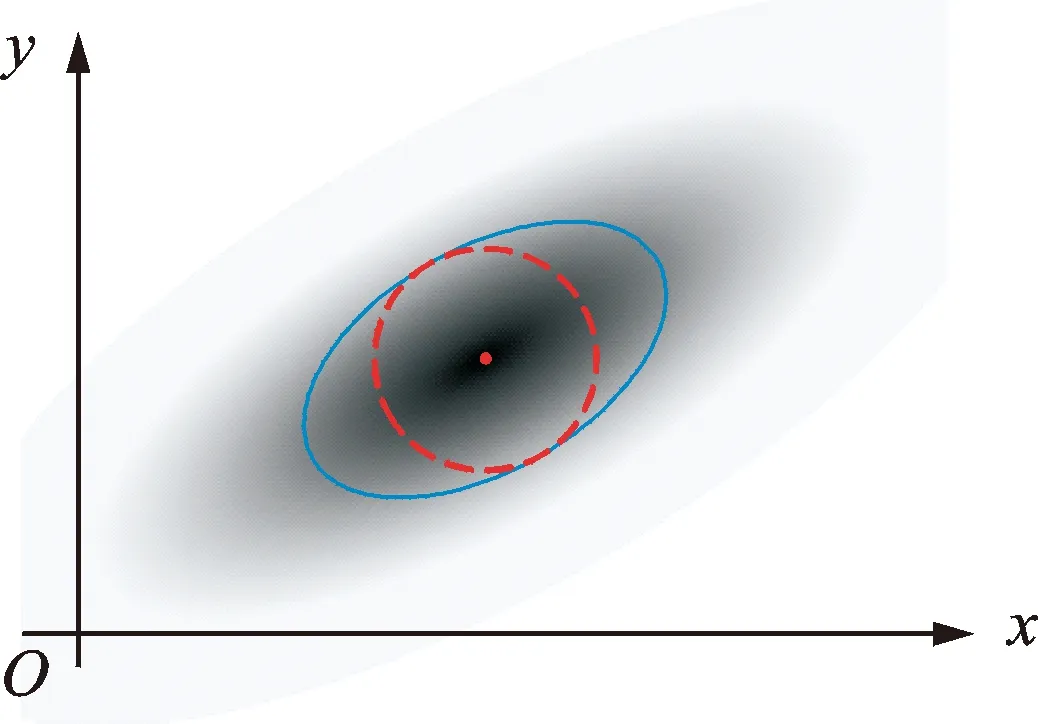
圖1 馬氏距離與歐氏距離Fig.1 Mahalanobis distance and Euclidean distance
基于馬氏距離數(shù)據(jù)分布特征描述方面的優(yōu)勢(shì),提出基于馬氏距離的樣本相似矩陣構(gòu)造方法,相似矩陣元素表達(dá)如下
(3)
其中:αij=exp(-dij/β);β為所有樣本之間馬氏距離均值的平方。

1.2 核密度估計(jì)調(diào)整
樣本近鄰構(gòu)造時(shí),空間中密集分布的樣本局部特征往往較為相似。對(duì)樣本xi來講,其附近區(qū)域其他樣本出現(xiàn)的概率密度越大,表示與其具有相似局部特征的樣本越多,則xi對(duì)應(yīng)的樣本近鄰數(shù)應(yīng)該大一些。據(jù)此提出將高斯核密度估計(jì)(Gauss kernel density estimation,簡(jiǎn)稱GKDE)[10]用于近鄰圖構(gòu)造,對(duì)基于相似系數(shù)均值Mi的自適應(yīng)近鄰結(jié)果進(jìn)行修正調(diào)整。
高斯核密度估計(jì)是一種非參數(shù)概率密度估計(jì)方法,能夠在樣本分布先驗(yàn)知識(shí)未知的情況下,根據(jù)樣本自身信息估計(jì)總體分布概率密度。高維空間RD中樣本xi的鄰域概率密度高斯核估計(jì)為
(4)
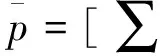
(5)
其中:floor表示數(shù)據(jù)向負(fù)無窮大方向取整。
通過式(5)可知,當(dāng)xi附近數(shù)據(jù)樣本分布密度大時(shí),該點(diǎn)的近鄰數(shù)自動(dòng)調(diào)整增大,當(dāng)其附近數(shù)據(jù)分布稀疏時(shí),近鄰數(shù)自動(dòng)調(diào)整減小。
1.3 自適應(yīng)鄰域構(gòu)造流程及特性
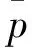
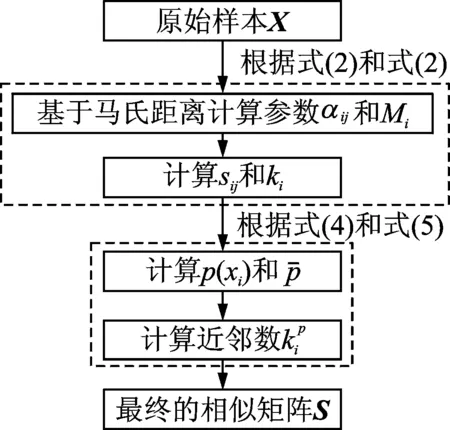
圖2 自適應(yīng)鄰域構(gòu)造流程Fig.2 Flow chart of adaptive neighborhood selection
自適應(yīng)鄰域構(gòu)造方法最終得到的相似矩陣S一般情況下是非對(duì)稱的,主要包含以下幾種情況:
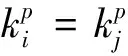
2) 與第1假設(shè)相同,當(dāng)樣本xi和xj互相不為近鄰時(shí),相似系數(shù)αij=αji=0,相似矩陣S對(duì)稱;
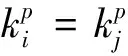
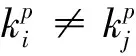
自適應(yīng)鄰域構(gòu)造方法與傳統(tǒng)k近鄰方法都是為了表達(dá)數(shù)據(jù)樣本局部結(jié)構(gòu)的相似性,主要不同為:
1) k近鄰方法基于歐氏距離計(jì)算樣本相似系數(shù),自適應(yīng)鄰域構(gòu)造方法基于馬氏距離計(jì)算相似系數(shù),能夠更好地考慮樣本分布特性;
2) k近鄰方法所有樣本近鄰數(shù)需人為設(shè)置,自適應(yīng)近鄰構(gòu)造方法根據(jù)相似系數(shù)均值Mi確定樣本初始近鄰數(shù),并采用樣本分布概率密度調(diào)整近鄰數(shù);
3) k近鄰方法所有樣本近鄰數(shù)均相等,自適應(yīng)近鄰構(gòu)造方法每個(gè)樣本的近鄰數(shù)不一定相等,且一般都不相等;
4) k近鄰方法得到的相似矩陣S是對(duì)稱的,自適應(yīng)近鄰構(gòu)造方法得到的相似矩陣S一般不對(duì)稱。
1.4 自適應(yīng)鄰域構(gòu)造實(shí)例
采用26個(gè)隨機(jī)二維數(shù)據(jù)樣本,說明自適應(yīng)鄰域構(gòu)造方法的特點(diǎn)。采用自適應(yīng)鄰域構(gòu)造方法尋找樣本近鄰,以樣本點(diǎn)A(1,4)和點(diǎn)B(8.5,5)的近鄰求解進(jìn)行說明,并給出k近鄰方法的對(duì)比,設(shè)定k=8。表1為自適應(yīng)近鄰求解過程中的參數(shù)及結(jié)果。圖3中4幅圖所示為原始26個(gè)樣本點(diǎn)及點(diǎn)A和點(diǎn)B的3種近鄰求解結(jié)果。
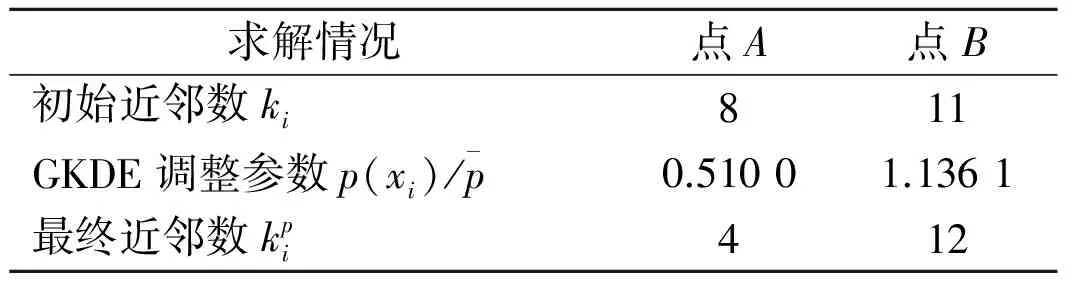
表1 近鄰求解參數(shù)及結(jié)果
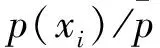
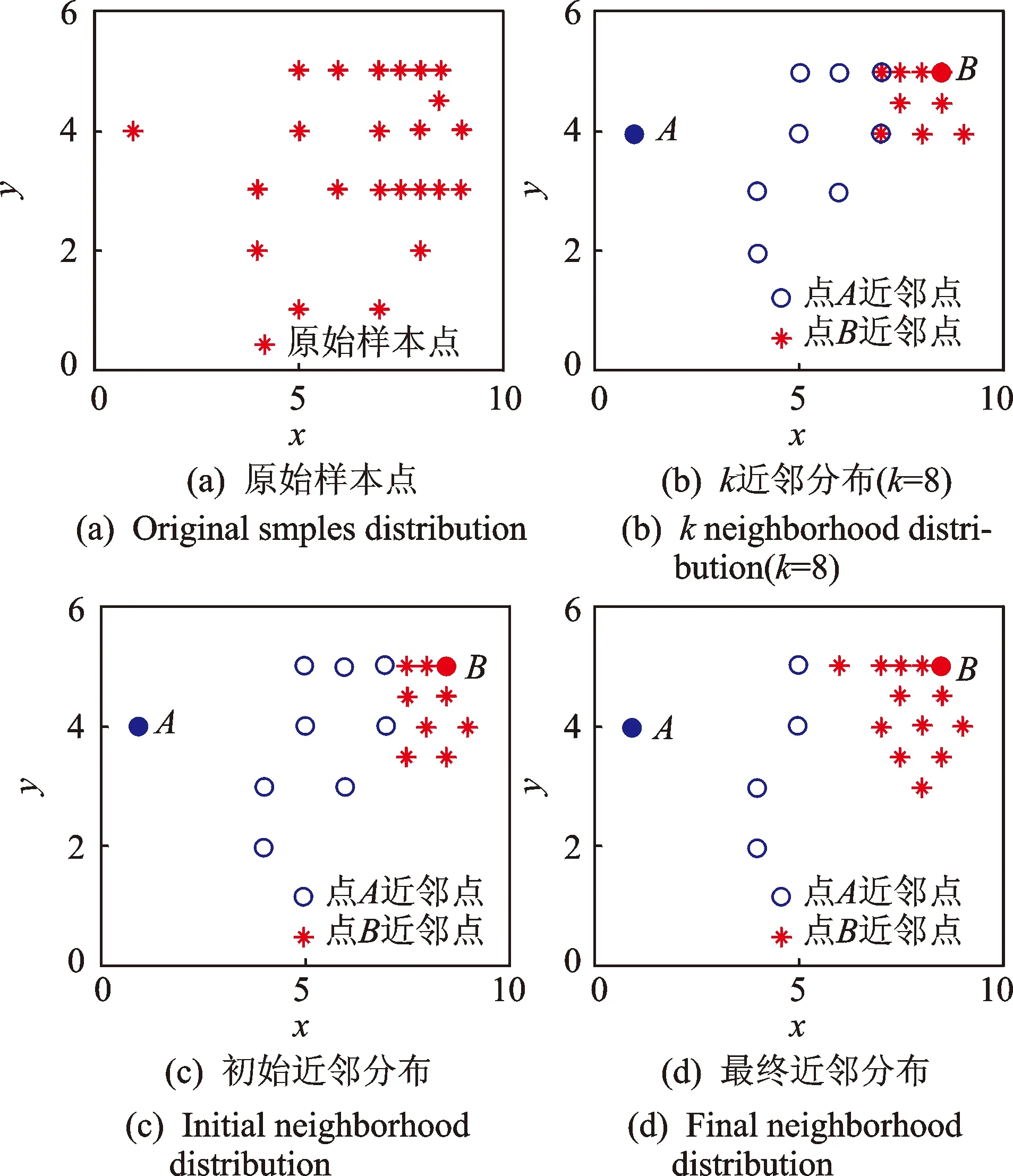
圖3 點(diǎn)A和點(diǎn)B近鄰結(jié)果分布Fig.3 Neighborhood for point A and point B
2 自適應(yīng)鄰域PCA-LPP流形學(xué)習(xí)算法
自適應(yīng)鄰域構(gòu)造方法能夠用于多種基于近鄰圖構(gòu)造的流形學(xué)習(xí)算法,筆者將其應(yīng)用于一種結(jié)合主元分析與局部保持投影的PCA-LPP改進(jìn)流形學(xué)習(xí)算法中,標(biāo)準(zhǔn)局部保持投影算法中相似矩陣S為對(duì)稱矩陣,其對(duì)稱性對(duì)算法的求解帶來很大便利。但自適應(yīng)鄰域構(gòu)造方法得到的相似矩陣S一般為非對(duì)稱矩陣,其在PCA-LPP中的求解推導(dǎo)如下。
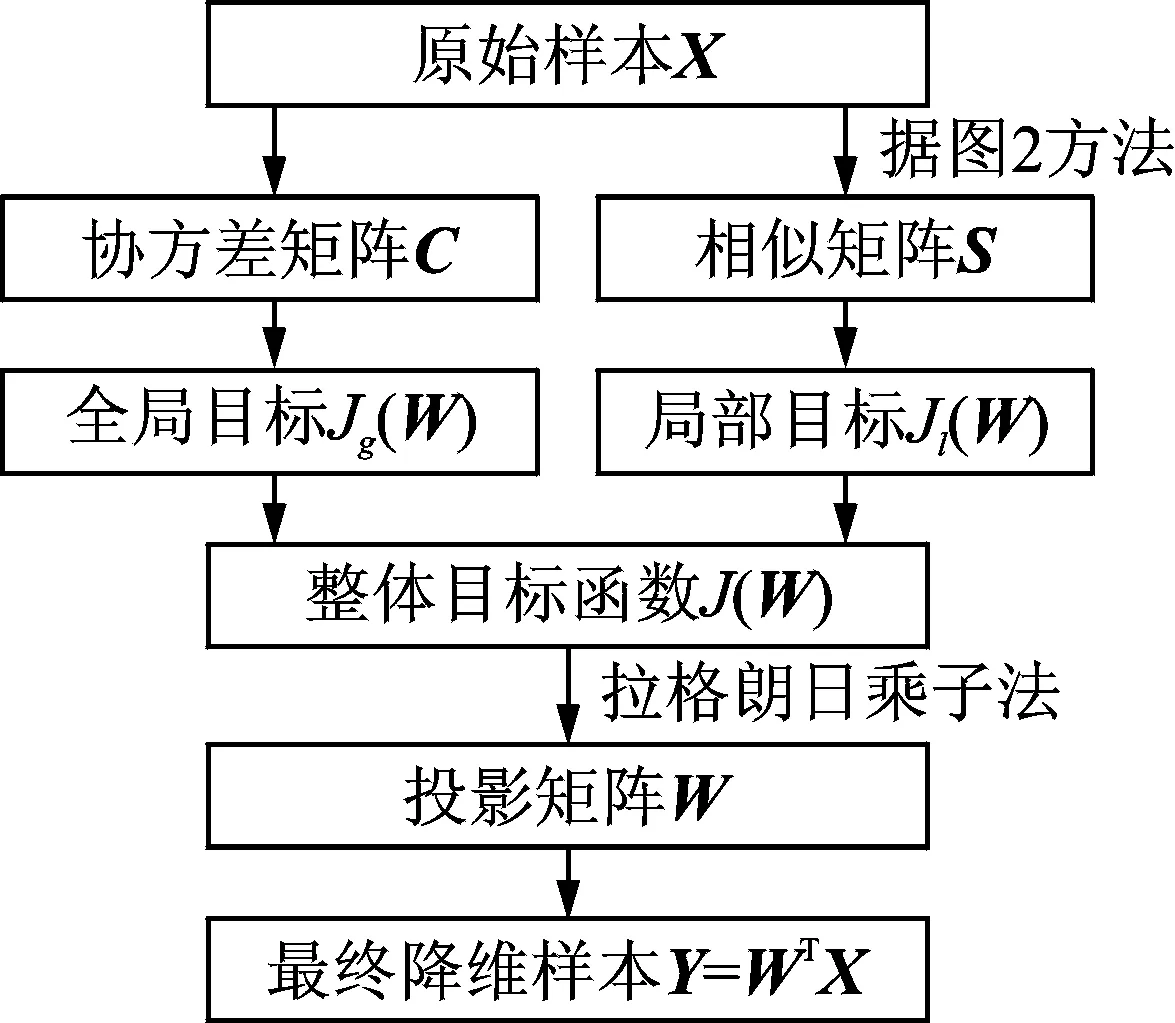
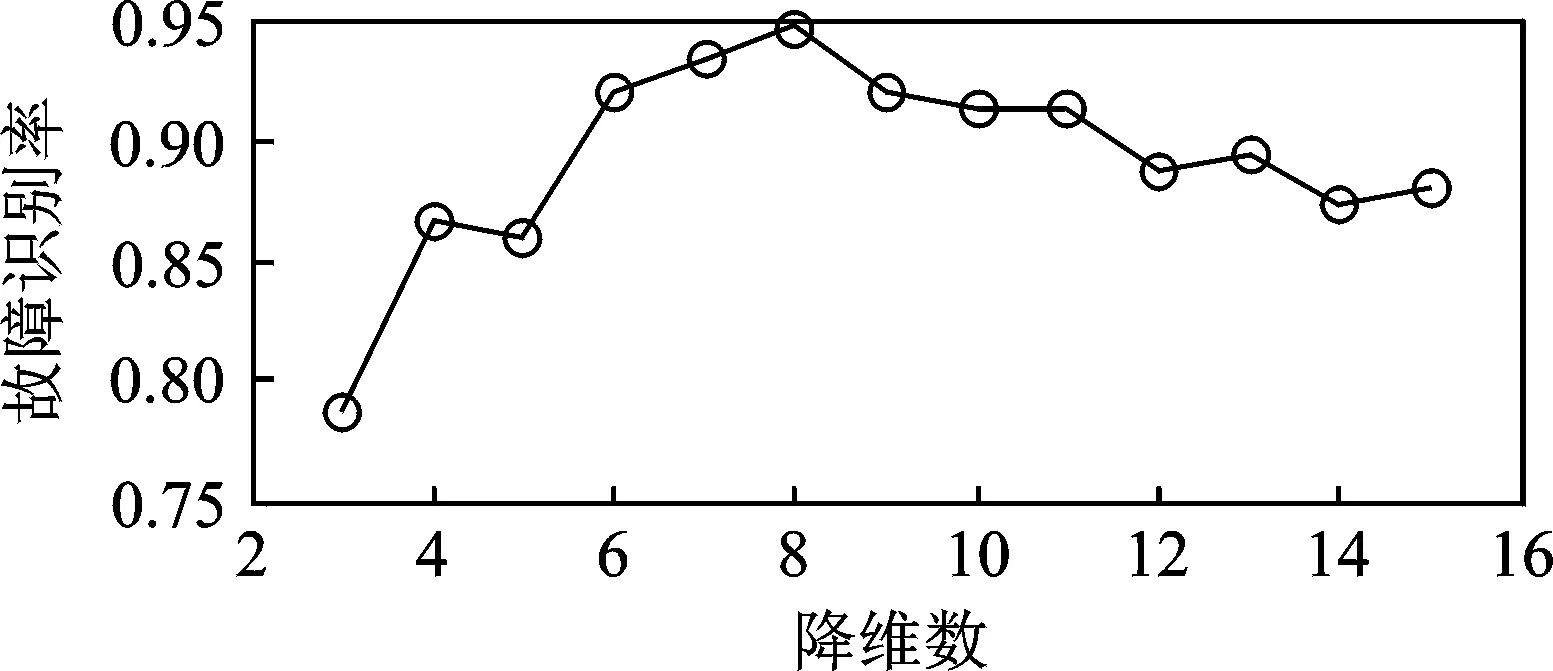
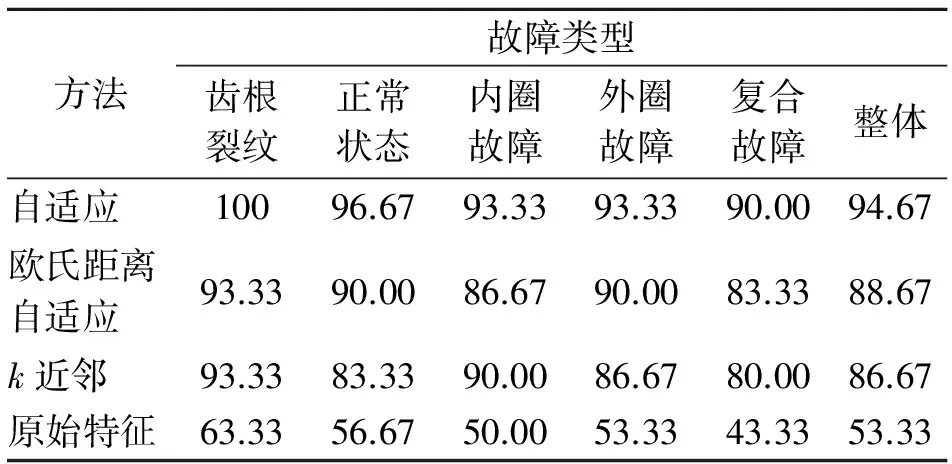
PCA-LPP流形學(xué)習(xí)目的在于將高維空間RD中的數(shù)據(jù)集X=[x1,x2,…,xN],通過投影矩陣W轉(zhuǎn)換投影到低維投影空間Rd(d PCA方法尋找數(shù)據(jù)分布方差最大的坐標(biāo)系,其全局目標(biāo)函數(shù)為 (6) LPP是一種非線性局部流形保持投影算法,能夠保持投影前后數(shù)據(jù)樣本間的局部結(jié)構(gòu)相似,其局部目標(biāo)函數(shù)為 (7) 其中:L′為拉普拉斯矩陣;Dii和Djj為對(duì)角陣,其元素為Dii=∑jsij,Djj=∑isij;D′=Dii+Djj;S′=S+ST;sij為相似系數(shù),構(gòu)成相似矩陣S;W為投影矩陣。 PCA-LPP流形學(xué)習(xí)算法兼顧PCA的全局分布方差最大特性及LPP的局部流形保持特性,能夠全面刻畫數(shù)據(jù)的整體和局部特征,其全局目標(biāo)函數(shù)為 (8) 其中:限定條件WTXD′XTW=I可消除隨機(jī)尺度因子的影響。 在LPP局部目標(biāo)函數(shù)中,自適應(yīng)鄰域構(gòu)造方法得到的相似矩陣S是非對(duì)稱矩陣,但局部目標(biāo)函數(shù)Jl(W)中的矩陣L′是對(duì)稱矩陣,其證明如下。 證明: ? 相似矩陣S ∵ Dii=∑jsij,Djj=∑isij均為對(duì)角陣 ∴ Dii和Djj為對(duì)稱矩陣 ∴ D′=Dii+Djj,S′=S+ST為對(duì)角對(duì)稱矩陣 ∴ L′=D′-S′為對(duì)稱矩陣。 自適應(yīng)鄰域構(gòu)造PCA-LPP算法的目標(biāo)函數(shù)式(8)可以通過拉格朗日乘子法[11],將其轉(zhuǎn)化為有約束最大值問題,如式(9)所示 (9) 式(9)對(duì)W求導(dǎo)并置零可得 (10) 化簡(jiǎn)式(10)可以得到 (C-XL′XT)W=λXD′XTW (11) 由式(11)可知,投影矩陣W的求解,實(shí)質(zhì)是廣義特征值求解問題,通過求取前d個(gè)最大特征值對(duì)應(yīng)的特征向量,從而得到投影矩陣W,投影后低維數(shù)據(jù)通過Y=WTX計(jì)算。 由此可以得到自適應(yīng)鄰域PCA-LPP流形學(xué)習(xí)算法流程,如圖4所示。 圖4 自適應(yīng)鄰域PCA-LPP算法流程Fig.4 PCA-LPP algorithm based on adaptive neighborhood 流形學(xué)習(xí)算法在數(shù)據(jù)可視化以及故障特征降維識(shí)別中應(yīng)用廣泛[12-13],下面對(duì)自適應(yīng)鄰域PCA-LPP流形學(xué)習(xí)算法的性能進(jìn)行驗(yàn)證。 采用齒輪箱故障實(shí)測(cè)聲發(fā)射信號(hào)對(duì)PCA-LPP的特征降維性能進(jìn)行驗(yàn)證。試驗(yàn)中齒輪箱故障包括正常狀態(tài)、軸承內(nèi)圈故障、外圈故障、內(nèi)外圈復(fù)合故障及齒根裂紋故障5種模式,故障軸承為6206,安裝在中間傳動(dòng)軸,故障齒輪為中間傳動(dòng)軸大齒輪,一級(jí)傳動(dòng)比為0.5,齒輪箱結(jié)構(gòu)原理及傳感器安裝如圖5所示。試驗(yàn)中齒輪箱空負(fù)載運(yùn)轉(zhuǎn),其輸入軸轉(zhuǎn)速為1 490 r/min。信號(hào)采集設(shè)備為北京軟島DS2-8A型全息聲發(fā)射信號(hào)分析儀,設(shè)置采集儀采樣頻率為1 MHz,采集儀硬件濾波參數(shù)為100 kHz~400 kHz帶通濾波,聲發(fā)射傳感器為聲華SR150M型,匹配40 dB前置放大器。每個(gè)數(shù)據(jù)樣本長(zhǎng)度為1 s,每種故障模式對(duì)應(yīng)70個(gè)樣本,5種模式共350個(gè)樣本。 對(duì)每個(gè)故障信號(hào)樣本進(jìn)行db4小波包4層分解,重構(gòu)各子頻帶小波包系數(shù),得到16個(gè)子頻帶重構(gòu)分量,各子頻帶寬度為31.25 kHz,計(jì)算子頻帶信號(hào)能量,得到能量特征向量E=[E1,E2,…,E16],求取16個(gè)子頻帶信號(hào)的能量熵作為特征向量[8],能量熵的計(jì)算方法如下。 (12) 采用自適應(yīng)鄰域PCA-LPP方法對(duì)所提故障特征向量進(jìn)行處理,并將降維后特征向量輸入支持向量機(jī)進(jìn)行訓(xùn)練識(shí)別,對(duì)比故障模式的分類識(shí)別性能,每個(gè)故障70個(gè)樣本中,40個(gè)用于訓(xùn)練支持向量機(jī)分類器,30個(gè)用于樣本故障分類識(shí)別。 3.1 自適應(yīng)鄰域PCA-LPP故障特征降維識(shí)別分析 齒輪箱故障聲發(fā)射信號(hào)的特征向量原始維度為16維,采用自適應(yīng)鄰域PCA-LPP對(duì)故障特征向量進(jìn)行降維處理,降維后特征的維度范圍為3~15維,間隔為1。不同降維數(shù)的特征向量輸入支持向量機(jī)的整體故障識(shí)別率如圖6所示。由圖6可以看到,原始的16維特征向量經(jīng)降維處理,不同維度的特征向量對(duì)應(yīng)的故障辨識(shí)率有所不同。辨識(shí)率在5維以后出現(xiàn)明顯增高,當(dāng)降維數(shù)d=8時(shí),整體故障辨識(shí)率最高,達(dá)到94.67%。其中整體故障辨識(shí)率指各單項(xiàng)故障識(shí)別率的均值,表示4種故障類型正確識(shí)別的總數(shù)占150個(gè)測(cè)試樣本的比例。 降維數(shù)d=8時(shí),不同故障的辨識(shí)率如表2所示。由表2可知,各類故障模式中,齒根裂紋辨識(shí)率最高,因?yàn)辇X根裂紋與其他幾種故障具有明顯不同,而復(fù)合故障辨識(shí)率最低,因?yàn)閺?fù)合故障與內(nèi)、外圈故障具有相似特征成分。 圖6 不同降維數(shù)的故障識(shí)別率Fig.6 Fault identification rate of different dimensions 故障類型齒根裂紋正常狀態(tài)內(nèi)圈故障外圈故障復(fù)合故障整體識(shí)別率%10096.6793.3393.3390.0094.67 3.2 不同識(shí)別方法性能對(duì)比 對(duì)文中的故障特征向量,將k近鄰PCA-LPP方法降維識(shí)別結(jié)果、基于歐氏距離的自適應(yīng)PCA-LPP方法降維識(shí)別結(jié)果以及原始特征向量不做任何處理的識(shí)別結(jié)果與3.1節(jié)的識(shí)別結(jié)果進(jìn)行對(duì)比,k近鄰方法的最優(yōu)識(shí)別結(jié)果通過交叉驗(yàn)證獲得。設(shè)置近鄰值k的變換范圍為5~30,間隔為1,降維數(shù)d的范圍為3~15,間隔為1,計(jì)算后得到k近鄰方法在k=17,d=7時(shí)獲得最高識(shí)別率。基于歐氏距離的自適應(yīng)PCA-LPP方法降維識(shí)別在降維數(shù)d=8時(shí)取得最高識(shí)別率。4種方法的識(shí)別率對(duì)比如表3所示。 表3 3種情況識(shí)別率對(duì)比 從表3可以看到,原始16維特征向量,不經(jīng)任何處理,直接進(jìn)行支持向量機(jī)分類器的訓(xùn)練和識(shí)別,其故障識(shí)別率最低,僅為53.33%,而采用流形學(xué)習(xí)算法降維之后,故障識(shí)別率明顯提升。對(duì)于同樣的PCA-LPP流形學(xué)習(xí)算法,不同的鄰域構(gòu)造方法帶來的降維效果差異較大。自適應(yīng)鄰域構(gòu)造方法降維后特征的故障識(shí)別率可達(dá)94.67%,而k近鄰方法降維后特征的故障識(shí)別率為86.67%。不同相似度衡量方法帶來的降維效果也不同,基于馬氏距離的相似度衡量最終故障識(shí)別率為94.67%,而基于歐氏距離的相似度衡量最終識(shí)別率卻為88.67%。原始特征向量維度高,其中包含故障特征的差異信息,但高維度同時(shí)包含過多的冗余信息,因此其故障識(shí)別率低。k近鄰方法對(duì)所有樣本采用相同的近鄰數(shù),對(duì)各樣本局部鄰域的描述不能做到分而劃之,基于歐氏距離的相似度衡量,對(duì)數(shù)據(jù)樣本的分布情況不能充分考慮,因此兩種方法特征向量的降維效果不如自適應(yīng)鄰域構(gòu)造方法,故其故障識(shí)別率低于自適應(yīng)鄰域PCA-LPP方法。 針對(duì)流形學(xué)習(xí)算法中近鄰圖的構(gòu)造問題,提出一種基于馬氏距離的相似矩陣元素計(jì)算。根據(jù)相似矩陣元素均值確定初始鄰域數(shù),并由數(shù)據(jù)樣本鄰域高斯核概率密度估計(jì)結(jié)果調(diào)整樣本近鄰數(shù),解決了自適應(yīng)構(gòu)造近鄰圖的問題。將自適應(yīng)鄰域構(gòu)造方法應(yīng)用于兼顧PCA與LPP二者特性的改進(jìn)流形學(xué)習(xí)算法,并給出相應(yīng)的理論計(jì)算模型,證明了求解拉普拉斯矩陣的對(duì)稱性。通過齒輪箱故障聲發(fā)射信號(hào)16維能量熵特征的降維識(shí)別對(duì)自適應(yīng)鄰域PCA-LPP流形學(xué)習(xí)算法的性能進(jìn)行驗(yàn)證,結(jié)果表明故障特征降到8維時(shí)識(shí)別率最高,可以達(dá)到94.67%。對(duì)比研究表明,自適應(yīng)鄰域構(gòu)造PCA-LPP方法的降維識(shí)別性能優(yōu)于k近鄰PCA-LPP方法以及原始特征向量的識(shí)別率。 [1] 趙振華,郝曉弘. 局部保持鑒別投影及其在人臉識(shí)別中的應(yīng)用[J]. 電子與信息學(xué)報(bào), 2013,35(2):463-466. Zhao Zhenhua, Hao Xiaohong. Linear locality preserving and discriminating projection for face recognition[J]. Journal of Electronics & Information Technology, 2013,35(2): 463-466.(in Chinese) [2] He Xiaofei, Niyogi P. Locality preserving projections[C]∥Neural Information Processing Systems16. Cambridge,USA: MIT Press, 2004:153-160. [3] 許慶誠(chéng),胡建中. 基于改進(jìn)增量LE的壓縮機(jī)故障特征提取方法[J]. 儀器儀表學(xué)報(bào),2013,34(4):791-796. Xu Qingcheng, Hu Jianzhong. Fault feature extraction method for compressor based on improved incremental Laplacian eigenmap algorithm[J]. Chinese Journal of Scientific Instrument, 2013,34(4):791-796.(in Chinese) [4] 何強(qiáng),蔡洪,韓壯志,等. 基于非線性流形學(xué)習(xí)的ISAR目標(biāo)識(shí)別研究[J]. 電子學(xué)報(bào), 2010,38(3):585-590. He Qiang, Cai Hong, Han Zhuangzhi, et al. ISAR target recognition based on non-linear manifold learning[J]. Acta Electronica Sinica,2010,38(3):585-590.(in Chinese) [5] Yang Bo, Chen Songcan. Sample-dependent graph construction with application to dimensionality reduction[J]. Neurocomputing, 2010,74(5): 301-314. [6] 劉鳳連,汪日偉,程俊,等. 圖像特征提取中領(lǐng)域尺寸和本征維數(shù)的自動(dòng)選擇算法[J]. 光電子·激光, 2013,24(12): 2416-2420. Liu Fenglian, Wang Riwei, Cheng Jun, et al. Auto-selected algorithm of the neighborhood size and intrinsic dimension for image feature extraction[J]. Journal fo Optoelectronics·Laser, 2013,24(12): 2416- 2420.(in Chinese) [7] 黃璞,唐振民. 無參數(shù)局部保持投影及人臉識(shí)別[J]. 模式識(shí)別與人工智能, 2013,26(9): 865-871. Huang Pu, Tang Zhenmin. Parameter-free locality preserving projections and face recognition[J]. Pattern Recognition and Artificial Intelligence, 2013,26(9): 865-871.(in Chinese) [8] 李城梁,王仲生,姜洪開,等. 自適應(yīng)Hessian LLE在機(jī)械故障特征提取中的應(yīng)用[J]. 振動(dòng)工程學(xué)報(bào), 2013,26(5): 758-763. Li Chengliang, Wang Zhongsheng, Jiang Hongkai, et al. Adaptive Hessian LLE in mechanical fault feature extraction[J]. Journal of Vibration Engineering,2013, 26(5): 758-763.(in Chinese) [9] 駱志高,李旭東,趙俊麗,等. 利用馬氏距離判別法準(zhǔn)確實(shí)現(xiàn)對(duì)裂紋的識(shí)別[J]. 振動(dòng)與沖擊,2013,32(21): 186-188. Luo Zhigao, Li Xudong, Zhao Junli, et al. Crack identification with mahalanobis distance discrimination method[J]. Journal of Vibration and Shock,2013,32(21): 186-188.(in Chinese) [10]孫即祥. 現(xiàn)代模式識(shí)別[M]. 長(zhǎng)沙:國(guó)防科技大學(xué)出版社,2002:136-140. [11]李鋒,王家序,楊榮松. 有監(jiān)督不相關(guān)正交局部保持映射故障辨識(shí)[J]. 儀器儀表學(xué)報(bào), 2013,34(5): 1113-1116. Li Feng, Wang Jiaxu, Yang Rongsong. Fault identification method on supervised uncorrelated orthogonal locality preserving projection[J]. Chinese Journal of Scientific Instrument,2013,34(5): 1113-1116.(in Chinese) [12]宋濤,湯寶平,李鋒. 基于流形學(xué)習(xí)和K-最近鄰分類器的旋轉(zhuǎn)機(jī)械故障診斷方法[J]. 振動(dòng)與沖擊,2013,32(5): 149-153. Song Tao, Tang Baoping, Li Feng. Fault diagnosis method for rotating machinery based on manifold learning and K-nearest neighbor classifier[J]. Journal of Vibration and Shock, 2013,32(5):149-153.(in Chinese) [13] 劉忠寶,潘廣貞,趙文娟. 流形判別分析[J]. 電子與信息學(xué)報(bào),2013,35(9):2047-2050. Liu Zhongbao, Pan Guangzhen, Zhao Wenjuan. Manifold-based discriminant analysis[J]. Journal of Electronics & Information Technology,2013,35(9): 2047-2050.(in Chinese) 10.16450/j.cnki.issn.1004-6801.2016.06.027 *國(guó)家自然科學(xué)基金資助項(xiàng)目(50775219) 2014-11-12; 2015-03-27 TH165; TN911 張曉濤,男,1987年5月生,博士生。主要研究方向?yàn)闄C(jī)械系統(tǒng)性能檢測(cè)與故障診斷。曾發(fā)表《基于SVD與Fast Kurtogram算法的滾動(dòng)軸承故障診斷》(《振動(dòng)與沖擊》2014年第33卷第10期)等論文。 E-mail:headic@163.com
3 齒輪箱故障特征降維分析

4 結(jié)束語(yǔ)


