一種空間微動(dòng)目標(biāo)寬帶雷達(dá)干涉三維成像方法
陳春暉 張 群 羅 迎 孫玉雪
?
一種空間微動(dòng)目標(biāo)寬帶雷達(dá)干涉三維成像方法
陳春暉 張 群*羅 迎 孫玉雪
(空軍工程大學(xué)信息與導(dǎo)航學(xué)院 西安 710077) (信息感知技術(shù)協(xié)同創(chuàng)新中心 西安 710077)
空間微動(dòng)目標(biāo)3維成像在目標(biāo)特征信息感知方面具有優(yōu)勢(shì),對(duì)于實(shí)施空間目標(biāo)成像、分類、識(shí)別等任務(wù)具有重要現(xiàn)實(shí)意義。據(jù)此,該文針對(duì)L型天線陣列成像系統(tǒng),提出一種基于改進(jìn)的粒子群優(yōu)化的空間微動(dòng)目標(biāo)寬帶雷達(dá)干涉式3維成像方法。首先,分析了目標(biāo)回波信號(hào)的微多普勒特性,建立參數(shù)化表征模型。其次,基于所提優(yōu)化算法重構(gòu)各天線回波信號(hào)的微多普勒相位項(xiàng),通過(guò)對(duì)各回波信號(hào)相位項(xiàng)的干涉處理,獲得干涉相位差,并推導(dǎo)干涉相位差與目標(biāo)空間坐標(biāo)的關(guān)系,從而重構(gòu)真實(shí)3維坐標(biāo),獲得微動(dòng)目標(biāo)3維圖像。相較于已有方法,所提方法基于干涉式成像思想,在無(wú)遮擋和有遮擋效應(yīng)的條件下,均可重構(gòu)微動(dòng)目標(biāo)真實(shí)空間坐標(biāo)和3維圖像,并且具有較好的魯棒性。最后,仿真計(jì)算驗(yàn)證了該方法的有效性。
雷達(dá)信號(hào)處理;3維成像;干涉成像;微動(dòng)目標(biāo);微多普勒效應(yīng)
1 引言
隨著航空航天技術(shù)的不斷發(fā)展,各類空間目標(biāo)的數(shù)量急劇增加,如何有效實(shí)現(xiàn)對(duì)空間目標(biāo)的探測(cè)、跟蹤、成像與識(shí)別等引起了廣泛關(guān)注。空間目標(biāo),如彈道導(dǎo)彈、太空碎片等,通常具有自旋、錐旋和進(jìn)動(dòng)等多種微動(dòng)形式,在雷達(dá)回波信號(hào)中產(chǎn)生微多普勒效應(yīng)[1,2]。據(jù)此開(kāi)展對(duì)空間微動(dòng)目標(biāo)成像方面的研究,對(duì)于保障我國(guó)空間安全等具有重要現(xiàn)實(shí)意義[3]。
在對(duì)空間微動(dòng)目標(biāo)成像的研究中,相較于采用逆合成孔徑雷達(dá)(Inverse Synthetic Aperture Radar, ISAR)實(shí)現(xiàn)目標(biāo)2維成像[4],3維成像在對(duì)目標(biāo)外形、體積、微動(dòng)參數(shù)等信息的感知方面具有顯著優(yōu)勢(shì)[5]。對(duì)于基于單基雷達(dá)的運(yùn)動(dòng)目標(biāo)3維成像方法[6,7],由于僅能觀測(cè)到目標(biāo)在雷達(dá)徑向距離上的微動(dòng)分量,因此,獲得的3維成像結(jié)果,不能確定目標(biāo)的真實(shí)空間位置,需要利用目標(biāo)相對(duì)于雷達(dá)的姿態(tài)信息,才能實(shí)現(xiàn)3維成像結(jié)果的準(zhǔn)確定標(biāo)。對(duì)于基于雙/多基地雷達(dá)的運(yùn)動(dòng)目標(biāo)3維成像方法[8,9],目標(biāo)散射中心各向異性、遮擋效應(yīng)等情況,將增加各雷達(dá)回波信號(hào)聯(lián)合處理的復(fù)雜性。此外,由于需要同時(shí)對(duì)多部雷達(dá)的回波信號(hào)進(jìn)行聯(lián)合處理,系統(tǒng)的實(shí)現(xiàn)也較復(fù)雜。近年來(lái),將干涉技術(shù)與ISAR成像相結(jié)合,組成干涉成像系統(tǒng),為實(shí)現(xiàn)運(yùn)動(dòng)目標(biāo)的3維成像提供了新途徑,比如基于L型陣列天線的干涉式成像系統(tǒng)。由已有文獻(xiàn)[10-13]的研究結(jié)果可知,對(duì)于惰性剛體運(yùn)動(dòng)目標(biāo),通過(guò)干涉式成像技術(shù)獲得目標(biāo)3維圖像,具有與目標(biāo)的物理尺寸相一致,能夠有效反映不受運(yùn)動(dòng)姿態(tài)影響的目標(biāo)穩(wěn)健特征信息等優(yōu)勢(shì),可為空間目標(biāo)分類、識(shí)別等提供有力的信息支撐。
在已有文獻(xiàn)的研究中,鮮有將干涉式成像方法用于實(shí)現(xiàn)空間微動(dòng)目標(biāo)3維成像,基于干涉式成像方法在3維成像研究中的優(yōu)勢(shì),本文將干涉成像的思想引入對(duì)空間微動(dòng)目標(biāo)3維成像的研究工作中。對(duì)于空間微動(dòng)目標(biāo),受限于雷達(dá)系統(tǒng)的脈沖重復(fù)頻率(Pulse Repetition Frequency, PRF),在ISAR成像所需小轉(zhuǎn)角內(nèi)的有效回波數(shù)量往往較少,使得傳統(tǒng)的ISAR成像效果不理想,無(wú)法有效區(qū)分各目標(biāo)散射點(diǎn),從而影響干涉處理,因此,已有的干涉式成像方法無(wú)法直接用于實(shí)現(xiàn)空間微動(dòng)目標(biāo)3維成像。針對(duì)該問(wèn)題,充分利用寬帶信號(hào)條件下由目標(biāo)微動(dòng)所引起的回波信號(hào)調(diào)制特征差異,從而區(qū)分各散射點(diǎn)的回波信號(hào),進(jìn)行有效的干涉處理。以空間自旋目標(biāo)為例,基于L型天線陣列成像系統(tǒng),提出了一種基于改進(jìn)的粒子群優(yōu)化的空間微動(dòng)目標(biāo)寬帶雷達(dá)干涉式3維成像方法,有效克服了單基雷達(dá)3維成像中難以獲得目標(biāo)真實(shí)空間坐標(biāo)和雙/多基地雷達(dá)3維成像中多部雷達(dá)回波信號(hào)聯(lián)合處理復(fù)雜等問(wèn)題。
2 微動(dòng)目標(biāo)回波信號(hào)模型
基于L型天線陣列干涉式成像系統(tǒng)如圖1中所示,坐標(biāo)系為雷達(dá)坐標(biāo)系,收發(fā)一體天線A位于坐標(biāo)原點(diǎn)(0, 0, 0)處。天線A和接收天線B, C構(gòu)成兩對(duì)分別沿著軸和軸方向的相互垂直的干涉基線,基線長(zhǎng)度為。接收天線B和C分別位于(, 0, 0)和(0, 0,)處。坐標(biāo)系為參考坐標(biāo)系,平行于雷達(dá)坐標(biāo)系,在目標(biāo)運(yùn)動(dòng)的起始時(shí)刻,坐標(biāo)原點(diǎn)在雷達(dá)坐標(biāo)系中的坐標(biāo)為(0,0,0),其方位角和仰角分別為和,點(diǎn)到天線A的位移矢量為A0。坐標(biāo)系為目標(biāo)本地坐標(biāo)系,其原點(diǎn)與參考坐標(biāo)系相同,為目標(biāo)中心。空間自旋目標(biāo)平動(dòng)速度為,以角速度和繞軸、軸和軸做旋轉(zhuǎn)運(yùn)動(dòng),其在目標(biāo)本地坐標(biāo)系中的角速度矢量為,其在參考坐標(biāo)系中的角速度矢量為。假設(shè)點(diǎn)為目標(biāo)上的一個(gè)散射點(diǎn),在起始時(shí)刻,在目標(biāo)本地坐標(biāo)系中的位置矢量為,在參考坐標(biāo)系中的位置矢量為。目標(biāo)本地坐標(biāo)系和參考坐標(biāo)系之間的關(guān)系為,其中,init為歐拉旋轉(zhuǎn)矩陣[14]。

圖1 干涉式成像系統(tǒng)及目標(biāo)模型
雷達(dá)發(fā)射線性調(diào)頻(Linear Frequency Modulation, LFM)信號(hào)為

(2)

圖2 第k個(gè)散射點(diǎn)空間旋轉(zhuǎn)運(yùn)動(dòng)及其與雷達(dá)之間的空間幾何關(guān)系投影圖

干涉式成像方法常用于對(duì)非合作運(yùn)動(dòng)目標(biāo)進(jìn)行3維成像,對(duì)于目標(biāo)分類和識(shí)別等具有重要意義。在已有研究中,鮮有將干涉式成像方法用于實(shí)現(xiàn)微動(dòng)目標(biāo)3維成像。本文將干涉式成像思想用于空間微動(dòng)目標(biāo)3維成像。基于干涉式成像思想,對(duì)第個(gè)散射點(diǎn),將天線A, B和C在距離-慢時(shí)間域的回波信號(hào)進(jìn)行干涉處理,可得到干涉相位差為
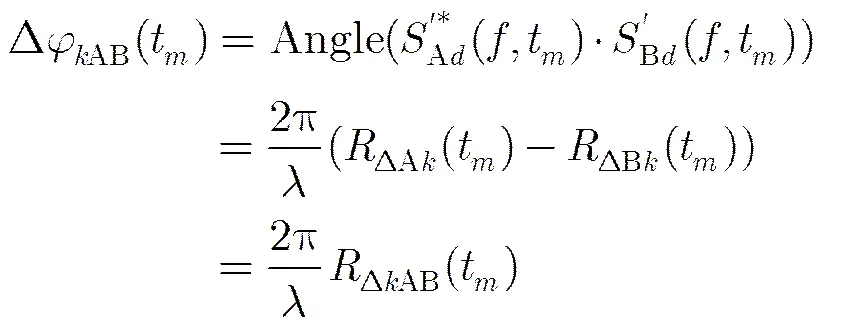
(5)
其中,Angle(·)表示取復(fù)數(shù)相位。得到第個(gè)散射點(diǎn)對(duì)于不同天線的干涉相位差后,可重構(gòu)其在參考坐標(biāo)系軸和軸的坐標(biāo)位置分別為

(7)
其在參考坐標(biāo)系軸的坐標(biāo)位置,可直接對(duì)距離-慢時(shí)間像進(jìn)行處理后獲得,具體方法在第3.2節(jié)中進(jìn)行分析。由此,在遠(yuǎn)場(chǎng)條件下,可獲得t時(shí)刻,第個(gè)散射點(diǎn)在參考坐標(biāo)系中的真實(shí)坐標(biāo)。對(duì)目標(biāo)上所有強(qiáng)散射點(diǎn)進(jìn)行干涉式成像處理后,即可獲得空間微動(dòng)目標(biāo)的3維圖像。
3 干涉式3維成像方法
3.1 改進(jìn)的單純形粒子群優(yōu)化算法
由式(6),式(7)可知,干涉式成像方法是通過(guò)不同天線之間的干涉相位差獲得目標(biāo)在參考坐標(biāo)系中的真實(shí)坐標(biāo)位置,因此,準(zhǔn)確重構(gòu)目標(biāo)在參考坐標(biāo)系中的真實(shí)坐標(biāo)與獲得干涉相位差關(guān)系密切,如何有效獲得干涉相位信息成為實(shí)現(xiàn)干涉式3維成像的關(guān)鍵。已有的微動(dòng)目標(biāo)參數(shù)估計(jì)方法[15],比如利用Hough變換方法提取微動(dòng)目標(biāo)參數(shù)[16],并不適用于對(duì)干涉相位信息的處理。為了有效獲取干涉相位信息,本文提出一種改進(jìn)的單純形粒子群算法,對(duì)目標(biāo)的特征參數(shù)進(jìn)行估計(jì),從而重構(gòu)目標(biāo)干涉相位信息,實(shí)現(xiàn)空間微動(dòng)目標(biāo)3維成像。
將收縮因子引入粒子群算法(Particle Swarm Optimization, PSO)算法,形成帶收縮因子的PSO算法(Constriction Factor PSO, CFPSO),可對(duì),1,2的取值進(jìn)行選擇,參數(shù)的引入平衡了群體的搜索能力和探索能力。在原有更新原則的基礎(chǔ)上乘一個(gè)收縮因子,其更新規(guī)則為

(9)
3.2 干涉式3維成像算法
以第個(gè)散射點(diǎn)為例,干涉式3維成像算法具體步驟如下:
步驟2 對(duì)回波信號(hào)的距離-慢時(shí)間像,利用數(shù)學(xué)形態(tài)學(xué)中的骨架提取算法進(jìn)行處理;
步驟3 根據(jù)骨架提取算法得到的結(jié)果,取第t時(shí)刻的回波信號(hào),和;
步驟5 利用改進(jìn)的單純形粒子群算法分別估計(jì)第個(gè)散射點(diǎn)的參數(shù)Ak,Bk,Ck,Ak,Bk,Ck,,;
步驟7 根據(jù)式(4),式(5)進(jìn)行干涉處理,計(jì)算干涉相位差和;
步驟8 根據(jù)式(6),式(7)計(jì)算第個(gè)散射點(diǎn)在參考坐標(biāo)系軸和軸的坐標(biāo)位置和;
步驟9 由1維距離像獲得第個(gè)散射點(diǎn)在參考坐標(biāo)系軸的坐標(biāo)位置;
步驟10 根據(jù)獲得的第個(gè)散射點(diǎn)在參考坐標(biāo)系中的坐標(biāo)(,,)重構(gòu)3維圖像。
對(duì)于目標(biāo)上的個(gè)散射點(diǎn),可同時(shí)重構(gòu)其在參考坐標(biāo)系中的坐標(biāo)(,,),,從而獲得目標(biāo)3維圖像。
4 仿真實(shí)驗(yàn)與分析
4.1 仿真實(shí)驗(yàn)
雷達(dá)發(fā)射LFM信號(hào),中心頻率f為10 GHz,帶寬為300 MHz,成像時(shí)間為1 s,脈沖重復(fù)頻率PRF為1000 Hz,脈寬T為,調(diào)頻率為。徑向距離分辨率為0.5 m,橫向距離分辨率為0.5 m。基線長(zhǎng)度為200 m,天線A, B和C在雷達(dá)坐標(biāo)系中的坐標(biāo)分別為(0, 0, 0) m, (200, 0, 0) m和(0, 0, 200) m。在初始時(shí)刻,目標(biāo)與雷達(dá)距離為500 km,3個(gè)散射點(diǎn)的旋轉(zhuǎn)中心在參考坐標(biāo)系中的坐標(biāo)分別為(0, 5.000, 0) m, (0, 2.000, 0) m和(0, -5.000, 0) m,旋轉(zhuǎn)角速度矢量為,位置矢量0分別為(4.000, 1.000, 4.000) m, (2.899, 6.450, -4.450) m和(-6.900, -5.450, 0.450) m,旋轉(zhuǎn)半徑矢量為(4.000, -4.000 4.000) m。
4.1.1 無(wú)遮擋效應(yīng) 對(duì)于目標(biāo)散射中心無(wú)遮擋情況,在成像時(shí)間內(nèi),散射點(diǎn)的旋轉(zhuǎn)軌跡包絡(luò)是連續(xù)完整的。由于天線A, B和C之間的距離相對(duì)于雷達(dá)與目標(biāo)之間的距離較小,所以在實(shí)圖像域,對(duì)于天線A, B和C得到的同一個(gè)散射點(diǎn)的距離-慢時(shí)間像差別較小。在成像時(shí)間內(nèi),目標(biāo)散射點(diǎn)在參考坐標(biāo)系軸,軸和軸的理論坐標(biāo),如圖3所示。
下面利用所提干涉式3維成像方法對(duì)目標(biāo)模型進(jìn)行仿真實(shí)驗(yàn)。對(duì)天線A, B和C的回波信號(hào)進(jìn)行分別處理后,可得到目標(biāo)模型的距離-慢時(shí)間像,利用數(shù)學(xué)形態(tài)學(xué)中的骨架提取算法對(duì)其進(jìn)行處理。然后,選取任意一個(gè)慢時(shí)間點(diǎn),獲得圖像中對(duì)應(yīng)的非零元素在回波信號(hào)矩陣中的位置,提取天線A對(duì)于目標(biāo)散射點(diǎn)在快時(shí)間頻率域的回波信號(hào)值。類似地,可提取天線B和C對(duì)于目標(biāo)散射點(diǎn)在快時(shí)間頻率域的回波信號(hào)值和。采用文中所提方法對(duì),和進(jìn)行處理。以散射點(diǎn)1為例,獲得各參數(shù)粗估計(jì)結(jié)果為,對(duì)各參數(shù)估計(jì)結(jié)果擴(kuò)展+/-10%,可得參數(shù)估計(jì)區(qū)間分別為[4.50, 5.50] m,[4.41, 5.39] m,[2.52, 3.08],[3.33, 4.07],利用所提算法對(duì)目標(biāo)參數(shù)進(jìn)行估計(jì),過(guò)程如圖4所示。由圖4可知,在估計(jì)過(guò)程中多次出現(xiàn)了局部極值點(diǎn)和停滯問(wèn)題,所提方法有效地跳出了局部極值點(diǎn),解決了停滯問(wèn)題,最終尋找到全局最優(yōu)解。基于所得參數(shù),計(jì)算,和。根據(jù)式(4),式(5),由所提方法可得到散射點(diǎn)1的干涉相位差和。再根據(jù)式(6),式(7)可計(jì)算得到散射點(diǎn)1在參考坐標(biāo)系軸和軸的坐標(biāo)位置1和1。同樣地,對(duì)散射點(diǎn)2和散射點(diǎn)3回波信號(hào)進(jìn)行求解,可分別重構(gòu)得到在參考坐標(biāo)系軸、軸的坐標(biāo)位置,結(jié)果如圖5所示,相應(yīng)的目標(biāo)散射點(diǎn)空間位置及旋轉(zhuǎn)軌跡如圖6所示。

圖3 參考坐標(biāo)系理論坐標(biāo)

圖4 對(duì)散射點(diǎn)1,天線A, B和C回波信號(hào)參數(shù)估計(jì)過(guò)程

圖5 重構(gòu)的參考坐標(biāo)系坐標(biāo)
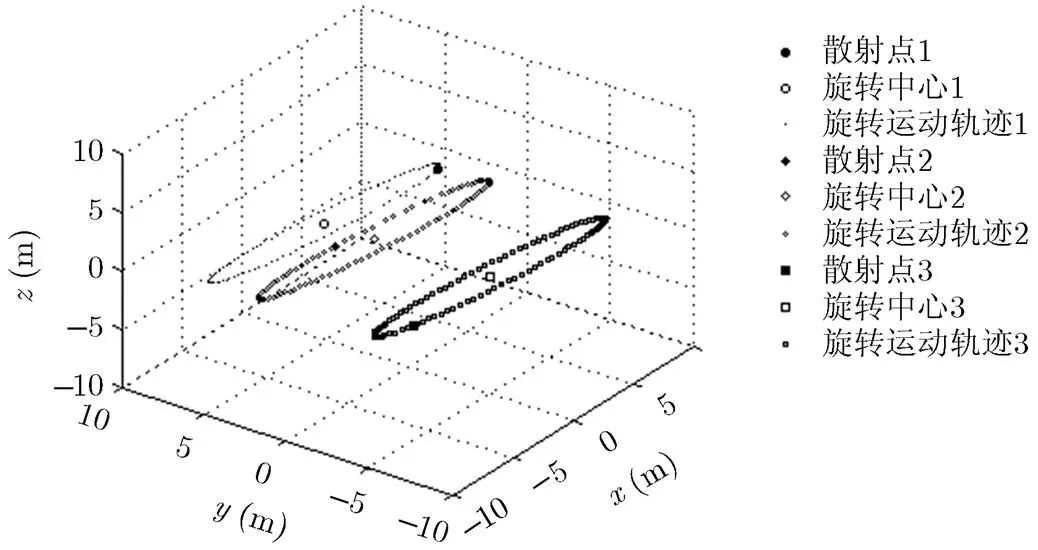
圖6 重構(gòu)的目標(biāo)模型空間3維圖像
4.1.2 有遮擋效應(yīng) 在實(shí)際應(yīng)用中,對(duì)于具有一定尺度的真實(shí)空間目標(biāo),由于其自旋運(yùn)動(dòng)時(shí),相對(duì)視角發(fā)生變化,當(dāng)目標(biāo)繞軸作自旋運(yùn)動(dòng)時(shí),目標(biāo)的散射中心在不同視角下會(huì)產(chǎn)生散射點(diǎn)的周期性遮擋效應(yīng),部分散射點(diǎn)對(duì)于雷達(dá)是不可見(jiàn)的,輪流被遮擋,導(dǎo)致回波距離像包絡(luò)出現(xiàn)局部的不完整性[17]。仿真實(shí)驗(yàn)中,以天線A為例,對(duì)目標(biāo)存在遮擋效應(yīng)時(shí)得到的距離-慢時(shí)間像,利用數(shù)學(xué)形態(tài)學(xué)中的骨架提取算法進(jìn)行處理。在有遮擋效應(yīng)條件下,距離-慢時(shí)間像包絡(luò)出現(xiàn)不連續(xù)的情況,當(dāng)任意選擇慢時(shí)間點(diǎn)時(shí),不可避免地會(huì)發(fā)生遺漏目標(biāo)散射點(diǎn)的情況。因此,需要對(duì)多個(gè)不同慢時(shí)間點(diǎn)所對(duì)應(yīng)的非零元素個(gè)數(shù)進(jìn)行估計(jì),選擇非零元素稀疏度最大時(shí)所對(duì)應(yīng)的慢時(shí)間點(diǎn),在目標(biāo)3維圖像重構(gòu)中,可有效降低由于遮擋效應(yīng)引起的散射點(diǎn)丟失的風(fēng)險(xiǎn)。同樣地,按照所提算法,對(duì)目標(biāo)散射點(diǎn)參數(shù)進(jìn)行估計(jì),重構(gòu)得到參考坐標(biāo)系坐標(biāo)如圖7所示。
4.2 分析與討論
在本節(jié)中,對(duì)影響所提方法成像性能的因素進(jìn)行了分析和討論,并將所提方法與文獻(xiàn)[18]的方法進(jìn)行了比較。
4.2.1 參數(shù)估計(jì)結(jié)果相對(duì)誤差對(duì)重構(gòu)結(jié)果的影響 由仿真實(shí)驗(yàn)結(jié)果可知,目標(biāo)參數(shù)估計(jì)結(jié)果與理論值之間存在誤差,本節(jié)針對(duì)參數(shù)估計(jì)誤差對(duì)空間3維坐標(biāo)重構(gòu)結(jié)果的影響進(jìn)行分析。以散射點(diǎn)1在參考坐標(biāo)系軸的重構(gòu)結(jié)果為例,分別假設(shè)參數(shù),,和的估計(jì)結(jié)果相對(duì)誤差分別為0.5%, 1.0%, 1.5%, 2.0%和2.5%, 50次蒙特卡羅仿真實(shí)驗(yàn)結(jié)果如圖8所示。由仿真實(shí)驗(yàn)結(jié)果可知,坐標(biāo)重構(gòu)結(jié)果對(duì)參數(shù),和的估計(jì)結(jié)果相對(duì)誤差不敏感,參數(shù)估計(jì)結(jié)果相對(duì)誤差對(duì)坐標(biāo)重構(gòu)結(jié)果造成的影響較小。然而,由圖8(b)可知,當(dāng)參數(shù)的估計(jì)結(jié)果相對(duì)誤差為2.5%時(shí),相應(yīng)的坐標(biāo)重構(gòu)結(jié)果相對(duì)誤差達(dá)到50%。因此,坐標(biāo)重構(gòu)結(jié)果對(duì)參數(shù)的估計(jì)結(jié)果相對(duì)誤差較敏感。
4.2.2 信噪比(Signal to Noise Ratio, SNR)對(duì)參數(shù)估計(jì)結(jié)果的影響 在4.2.1節(jié)中分析了參數(shù)估計(jì)結(jié)果相對(duì)誤差對(duì)重構(gòu)結(jié)果的影響,而SNR是影響參數(shù)估計(jì)結(jié)果的重要因素,因此,針對(duì)SNR變化對(duì)參數(shù)估計(jì)結(jié)果的影響進(jìn)行分析和討論。仿真實(shí)驗(yàn)中,取SNR分別為0 dB, 5 dB, 10 dB, 15 dB和20 dB,對(duì)散射點(diǎn)1的天線A回波信號(hào)進(jìn)行參數(shù)估計(jì),50次蒙特卡羅仿真結(jié)果如圖9所示。由圖9中的仿真實(shí)驗(yàn)結(jié)果可知,和的估計(jì)結(jié)果對(duì)SNR的變化不敏感,當(dāng)SNR為0 dB時(shí),估計(jì)結(jié)果的相對(duì)誤差仍很小;參數(shù)和的估計(jì)結(jié)果對(duì)SNR的變化較敏感。由4.2.1節(jié)中的分析可知,參數(shù)的估計(jì)結(jié)果相對(duì)誤差對(duì)重構(gòu)結(jié)果影響較小,因此,綜合以上因素,當(dāng)SNR為0 dB時(shí),參數(shù)的估計(jì)結(jié)果相對(duì)誤差為2.0%,對(duì)坐標(biāo)重構(gòu)結(jié)果的影響仍較小。對(duì)于參數(shù),當(dāng)SNR為5 dB時(shí),其估計(jì)結(jié)果相對(duì)誤差為0.75%,由圖8(b)中的結(jié)果可知,重構(gòu)結(jié)果相對(duì)誤差為15%,對(duì)重構(gòu)結(jié)果造成了較大影響。因此,綜合上述分析結(jié)果可知,在SNR高于5 dB的條件下,基于所提方法可較準(zhǔn)確地重構(gòu)目標(biāo)真實(shí)3維坐標(biāo)。
4.2.3 與已有方法的比較 由于干涉方法對(duì)回波信號(hào)相位項(xiàng)變化的敏感性,因此,對(duì)各散射點(diǎn)回波信號(hào)進(jìn)行區(qū)分的方法應(yīng)具有較好的相位保持性。若處理后的回波信號(hào)相位項(xiàng)發(fā)生較大改變,那么將難以準(zhǔn)確重構(gòu)目標(biāo)的真實(shí)3維坐標(biāo)。在已有方法中[18],往往首先對(duì)各散射點(diǎn)的1維距離像進(jìn)行曲線分離處理,然后對(duì)各散射點(diǎn)回波信號(hào)分別進(jìn)行干涉處理。該類方法的優(yōu)點(diǎn)在于具有較好的相位保持性;缺點(diǎn)在于在曲線分離處理中,對(duì)曲線交叉點(diǎn)進(jìn)行處理時(shí),不可避免地在交叉點(diǎn)處出現(xiàn)分離錯(cuò)誤的情況,此外,對(duì)于存在遮擋效應(yīng)的情況,距離-慢時(shí)間像的包絡(luò)不連續(xù),也嚴(yán)重影響曲線分離方法的結(jié)果[19],有待進(jìn)一步深入研究。因此,與已有方法相比,在無(wú)遮擋和有遮擋效應(yīng)的情況下,所提方法均能夠準(zhǔn)確重構(gòu)目標(biāo)真實(shí)3維坐標(biāo)。

圖7 重構(gòu)的參考坐標(biāo)系坐標(biāo)

圖8 參數(shù)估計(jì)結(jié)果相對(duì)誤差對(duì)坐標(biāo)重構(gòu)結(jié)果的影響???????圖9 SNR對(duì)參數(shù)估計(jì)結(jié)果的影響
5 結(jié)論
針對(duì)空間微動(dòng)目標(biāo)寬帶雷達(dá)3維成像問(wèn)題,本文提出了一種基于改進(jìn)的粒子群優(yōu)化的干涉式3維成像方法。所提方法通過(guò)建立回波信號(hào)參數(shù)化表征模型、微多普勒相位重構(gòu)、相位干涉等計(jì)算和處理,利用回波信號(hào)干涉相位差,重構(gòu)空間微動(dòng)目標(biāo)真實(shí)坐標(biāo)和3維圖像。相較于已有方法,所提方法在無(wú)遮擋和有遮擋效應(yīng)的條件下,均可準(zhǔn)確重構(gòu)目標(biāo)空間坐標(biāo)和3維圖像,并具有較好的魯棒性,為有效實(shí)現(xiàn)空間微動(dòng)目標(biāo)3維成像提供了一種思路。仿真結(jié)果驗(yàn)證了所提方法的有效性。
參考文獻(xiàn)
[1] 張群, 羅迎. 雷達(dá)目標(biāo)微多普勒效應(yīng)[M]. 北京: 國(guó)防工業(yè)出版社, 2013: 22-23.
ZHANG Q and LUO Y. Micro-Doppler Effect of Radar Targets[M]. Beijing: National Defense Industry Press, 2013: 22-23.
[2] 王德純. 微多普勒雷達(dá)述評(píng)[J]. 中國(guó)電子科學(xué)研究院學(xué)報(bào), 2012, 7(6): 575-580. doi: 10.3969/j.issn.1673-5692.2012.06. 006.
WANG Dechun. An overview of micro-Doppler radar[J]., 2012, 7(6): 575-580. doi: 10.3969/j.issn. 1673-5692.2012.06.006.
[3] 張浩鵬, 魏全茂, 張威, 等. 基于序列圖像的空間目標(biāo)三維重建[J]. 北京航空航天大學(xué)學(xué)報(bào), 2016, 42(2): 273-279. doi: 10.13700/j.bh.1001-5965.2015.0117.
ZHANG Haopeng, WEI Quanmao, ZHANG Wei,. Sequential image based space object 3D reconstruction[J]., 2016, 42(2): 273-279. doi: 10.13700/j.bh.1001-5965.2015. 0117.
[4] LIU Hongchao, JIU Bo, LIU Hongwei,. Super-resolution ISAR imaging based on sparse Bayesian learning[J]., 2014, 52(8): 5005-5013. doi: 10.1109/TGRS.2013.2286402.
[5] BAI Xueru, ZHOU Feng, and BAO Zheng. High-resolution three-dimensional imaging of space targets in micro-motion [J]., 2015, 8(7): 3428-3440. doi: 10.1109/JSTARS.2015.2431119.
[6] MAYHAN J T. Phase-enhanced 3D snapshot ISAR imaging and interferometric SAR[R]. ESC-TR-2007-067, Lexington: Lincoln Laboratory, 2009.
[7] 王昕, 郭寶鋒, 尚朝軒. 基于二維ISAR圖像序列的雷達(dá)目標(biāo)三維重建方法[J]. 電子與信息學(xué)報(bào), 2013, 35(10): 2475-2480. doi: 10.3724/SP.J.1146.2013.00140.
WANG Xin, GUO Baofeng, and SHANG Chaoxuan. 3D reconstruction of target geometry based on 2D data of inverse synthetic aperture radar images[J].&, 2013, 35(10): 2475-2480. doi: 10. 3724/SP.J.1146.2013.00140.
[8] 梁必帥, 張群, 婁昊, 等. 基于微動(dòng)特征關(guān)聯(lián)的空間自旋目標(biāo)寬帶雷達(dá)三維成像[J]. 電子與信息學(xué)報(bào), 2013, 35(9): 2132-2140. doi: 10.3724/SP.J.1146.2012.01537.
LIANG Bishuai, ZHANG Qun, LOU Hao,. Three- dimensional broadband radar imaging of space spinning targets based on micro-motion parameter correlation[J].&, 2013, 35(9): 2132-2140. doi: 10.3724/SP.J.1146.2012.01537.
[9] 梁必帥, 張群, 婁昊, 等. 基于微動(dòng)特征關(guān)聯(lián)的空間非對(duì)稱自旋目標(biāo)雷達(dá)三維成像方法[J]. 電子與信息學(xué)報(bào), 2014, 36(6): 1381-1388. doi: 10.3724/SP.J.1146.2013.01147.
LIANG Bishuai, ZHANG Qun, LOU Hao,. A method of three dimensional imaging based on micro-motion feature association for spatial asymmetrical spinning targets[J].&, 2014, 36(6): 1381-1388. doi: 10.3724/SP.J.1146.2013.01147.
[10] WANG Genyuan, XIA Xianggen, and CHEN V C. Three- dimensional ISAR imaging of maneuvering targets using three receivers[J]., 2001, 10(3): 436-447. doi: 10.1109/83.908519.
[11] ZHAO Lizhi, GAO Meiguo, MARTORELLA M,. Bistatic three-dimensional interferometric ISAR image reconstruction[J]., 2015, 51(2): 951-961. doi: 10.1109/TAES. 2014.130702.
[12] LIU C L, HE F, GAO X Z,. Squint-mode InISAR imaging based on nonlinear least square and coordinates transform[J]., 2011, 54(12): 3332-3340. doi: 10.1007/s11431-011-4515-9.
[13] 劉波, 潘舟浩, 李道京, 等. 基于毫米波InISAR成像的運(yùn)動(dòng)目標(biāo)探測(cè)與定位[J]. 紅外與毫米波學(xué)報(bào), 2012, 31(3): 258-264. doi: 10.3724/SP.J.1010.2012.00258.
LIU Bo, PAN Zhouhao, LI Daojing,. Moving target detection and location based on millimeter-wave InISAR imaging[J]., 2012, 31(3): 258-264. doi: 10.3724/SP.J.1010.2012.00258.
[14] CHEN V C, LI F Y, HO S S,. Micro-Doppler effect in radar: Phenomenon, model and simulation study[J]., 2006, 42(1): 2-21. doi: 10.1109/TAES.2006.1603402.
[15] 曹文杰, 張磊, 杜蘭, 等. 基于瞬時(shí)頻率估計(jì)的進(jìn)動(dòng)錐體目標(biāo)微多普勒頻率提取方法[J]. 電子與信息學(xué)報(bào), 2015, 37(5): 1091-1096. doi: 10.11999/JEIT140985.
CAO Wenjie, ZHANG Lei, DU Lan,. Micro-Doppler frequency extraction for cone-shaped target with precession based on instantaneous frequency estimation[J].&, 2015, 37(5): 1091-1096. doi: 10.11999/JEIT140985.
[16] ZHANG Q, YEO T S, TAN H S,. Imaging of a moving target with rotating parts based on the Hough transform[J]., 2008, 46(1): 291-299. doi: 10.1109/TGRS.2007.907105.
[17] HONG Ling, DAI Fengzhou, and LIU Hongwei. Sparse narrowband radar imaging for spinning targets with occlusion effect[C]. IEEE International Radar Conference, Arlington, USA, 2015: 942-946. doi: 10.1109/RADAR.2015. 7131130.
[18] SUN Yuxue, MA Changzheng, LUO Ying,. An interferometric-processing based three-dimensional imaging method for space rotating targets[C]. IET International Radar Conference, Guangzhou, China, 2016: 398-402.
[19] 趙盟盟, 張群, 陳怡君, 等. 一種用于空間群目標(biāo)分辨的滑動(dòng)窗軌跡跟蹤算法[J]. 宇航學(xué)報(bào), 2015, 36(10): 1187-1194. doi: 10.3873/j.issn.1000-1328.2015.10.013.
ZHAO Mengmeng, ZHANG Qun, CHEN Yijun,. A sliding window tracking algorithm for distinguishing space group targets[J]., 2015, 36(10): 1187-1194. doi: 10.3873/j.issn.1000-1328.2015.10.013.
陳春暉: 女,1986年生,工程師,研究方向?yàn)槔走_(dá)運(yùn)動(dòng)目標(biāo)成像與識(shí)別.
張 群: 男,1964年生,教授,研究方向?yàn)槔走_(dá)成像與目標(biāo)識(shí)別.
羅 迎: 男,1984年生,副教授,研究方向?yàn)槔走_(dá)成像與目標(biāo)識(shí)別.
孫玉雪: 女,1992年生,研究生,研究方向?yàn)槔走_(dá)成像與目標(biāo)識(shí)別.
Interferometric Three Dimensional Imaging Method for Space Micro-motion Target Based on Wideband Radar
CHEN Chunhui ZHANG Qun LUO Ying SUN Yuxue
(,,’710077,) (,’710077,)
Three dimensional imaging of space micro-motion target has significant advantages on target information awareness, which is crucial to effectively realize space target imaging, classification and recognition. In this paper, through the L type antenna array imaging system, an interferometric three dimensional imaging method for space micro-motion target is proposed based on the improved Particle Swarm Optimization (PSO) algorithm. Firstly, the Doppler effect in the received signal is analyzed, and the corresponding parametric model is established. Then, the Doppler phase term of the received signal is reconstructed by using the proposed optimization method. Through interferometric processing and analyzing the quantitative relationship between interferometric phase difference and real coordinate, the three dimensional coordinates and image can be obtained. Compared with the existing methods, the proposed method can reconstruct the real coordinates and three dimensional image of micro-motion target with and without occlusion effect. It also has good robustness. Finally, simulations validate the effectiveness of the proposed method.
Radar signal processing; Three dimensional imaging; Interferometric imaging; Micro-motion target; Micro-Doppler effect
TN957.52
A
1009-5896(2016)12-3144-08
10.11999/JEIT161025
2016-10-08;改回日期:2016-11-17;
2016-12-14
張群 afeuzq@163.com
國(guó)家自然科學(xué)基金(61571457)
The National Natural Science Foundation of China (61571457)

