基于“當前”統計模型的交互式粒子濾波算法
馬瑩
(長春建筑學院,吉林 長春 130607)
基于“當前”統計模型的交互式粒子濾波算法
馬瑩
(長春建筑學院,吉林 長春 130607)
通過CV和CA模型對非機動和弱機動目標進行建模,采用“當前”統計模型的交互式模型的粒子濾波算法,并匹配卡爾曼濾波算法。該算法與傳統的IMMPF濾波算法相比,顯著的降低運算量,并提高其目標的跟蹤精度。 仿真結果證明了該算法在機動目標跟蹤的性能上有所改善,并降低了經典交互式粒子濾波算法的復雜程度,使其更具有實時性。
目標跟蹤;“當前”統計模型;交互式模型;粒子濾波
0 引言
目標跟蹤問題是數據融合的一個重要的研究課題,得到了人們的廣泛研究。其中機動目標建模和濾波算法的研究一直是目標跟蹤領域的研究重點。本文為解決傳統跟蹤算法在高度非線性、非高斯模型中難以準確描述高機動目標的運動狀態,通過在傳統算法中加入“當前”統計模型,并匹配粒子濾波算法提高高機動目標的跟蹤精度;而對低機動的CV和CA模型采用卡爾曼濾波,本文提出的算法顯著降低了計算量,并提高了對機動目標的跟蹤精度。
1 “當前”統計模型
目標的“當前”統計(CS-Current Statstic)模型在Singer模型上進一步發展。建立一種非零均值時間的目標加速度模型。

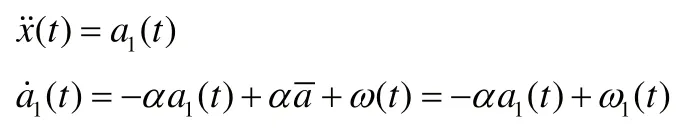
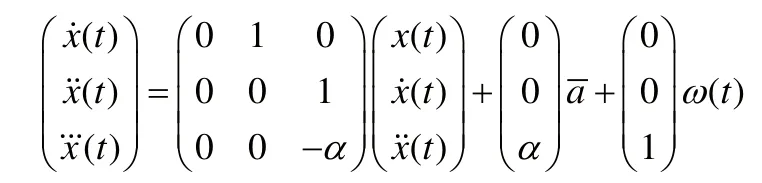
其中,x,x˙,x˙分別為運動目標的位置,速度和加速度分量。
將上式離散化得到如下形式:
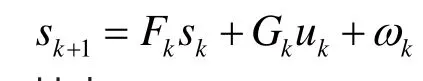
其中:
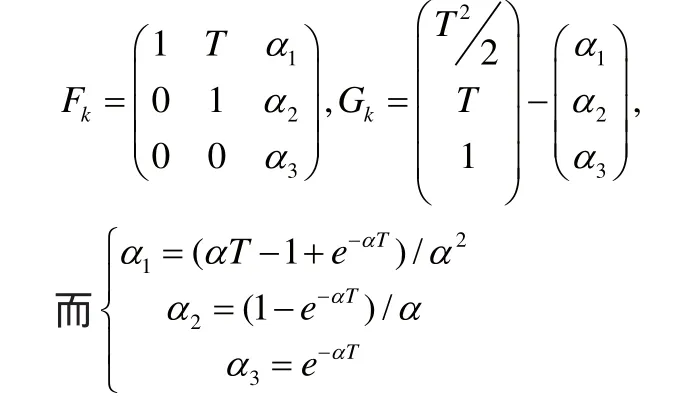
其中,ku為“當前”加速度均值,T為采樣周期,α為機動頻率,過程噪聲kω是均值為零,方差為 ()Q k的高斯白噪聲。
“當前”加速度的方差2aσ為:和分別為最大正負加速度。
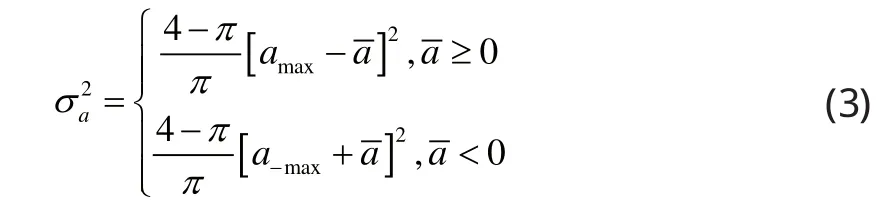
2 交互式多模型算法
假設一個混合系統的離散化狀態方程和觀測方程為:
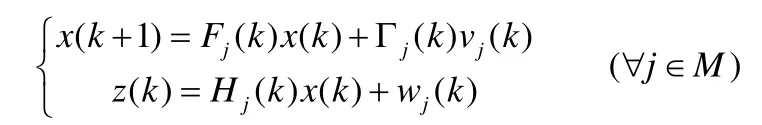
2.1 輸入交互( )j M?∈
輸入交互概率
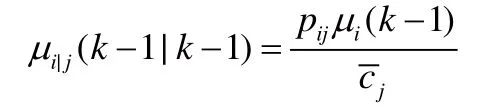
其中:
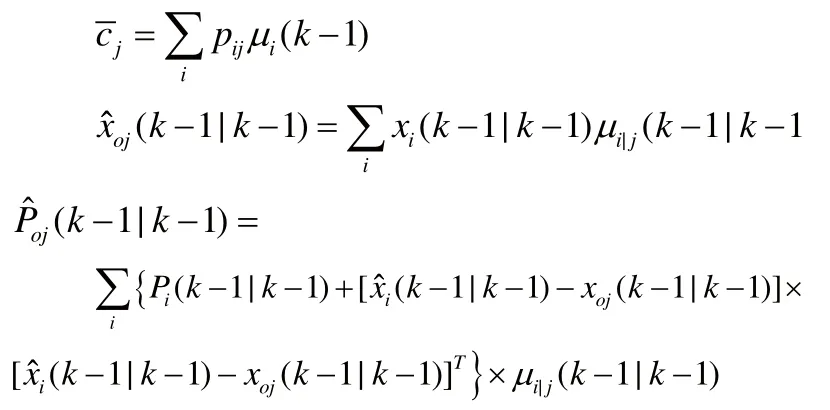
2.2 組合輸出

3 “當前”統計模型交互式粒子濾波算法
以交互式多模型算法為框架,多模型的模型集合M采用CV模型、CA模型和“當前”統計模型,其中“當前”統計模型利用模型概率和狀態估計值調整參數和的取值。
3.1 輸入交互
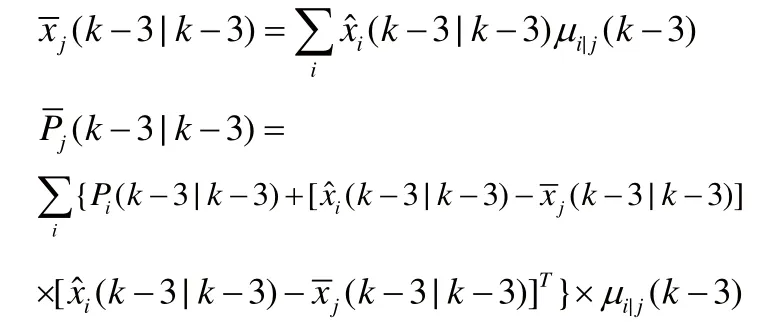
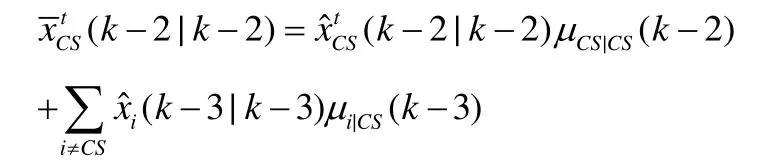
3.2 輸出交互
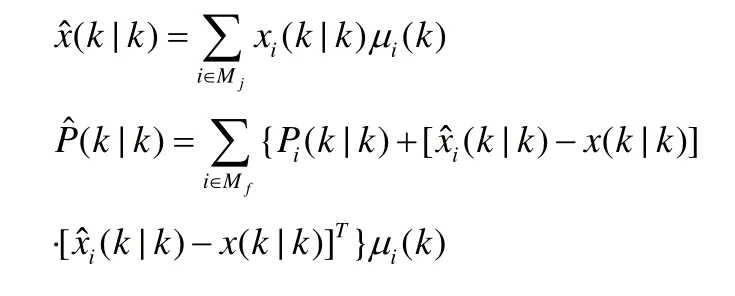
4 “當前”統計模型交互式粒子濾波算法仿真
設目標的運動軌跡如下:
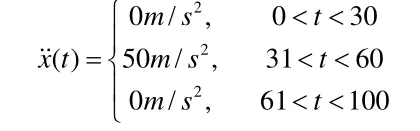
構造IMM的三個模型:模型1為常加速(CV)模型,模型2為常加速度(CA)模型,模型3為“當前”統計模型。
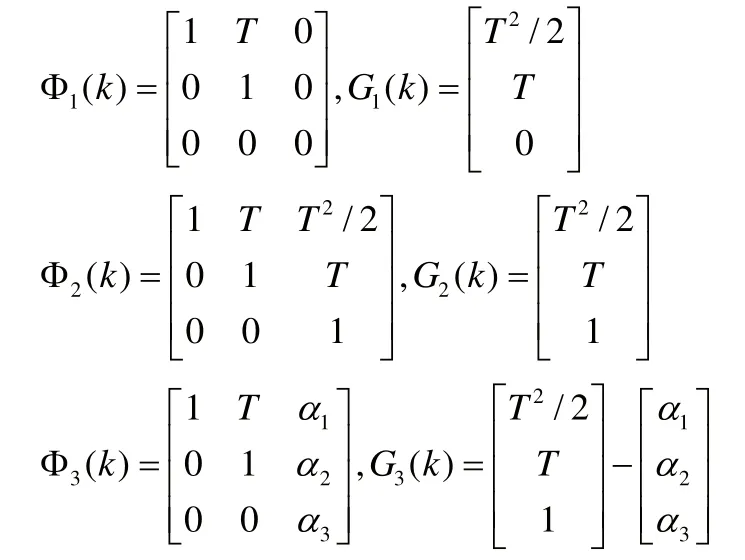
采樣周期T=1s,粒子濾波的粒子數為N=100。
蒙特卡羅仿真次數為100。仿真中,本文的算法與通用的交互式粒子濾波算法(IMMPF)進行了比較,圖1、2、3分別顯示了位置、x軸、y軸的估計均方根誤差。
如圖1、2、3所示在目標常速運動時,兩種算法均能較好的反映目標的運動狀態。當目標發生機動時,從仿真圖中可以看出本算法的位置、x軸、y軸的均方根誤差都要小于IMMPF算法。因而本算法優于IMMPF算法。
5 結論
交互式多模型是一種次優混合濾波算法,具有自動調整濾波帶寬的特點。在目標非機動,機動時的各種濾波算法具有顯著成效,既能解決自適應濾波算法又能克服了檢測自適應濾波算法在目標機動時濾波效果差的缺點。
本文新濾波算法結合IMM算法和粒子濾波,即使在非線性、非高斯等限制問題,也能夠跟蹤目標的任意機動。仿真實驗,結果證實了本文提出的目標跟蹤新算法跟蹤效果優于通用的IMMPF算法。
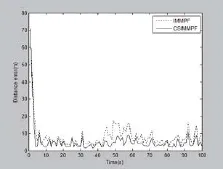
圖1 位置估計均方根誤差
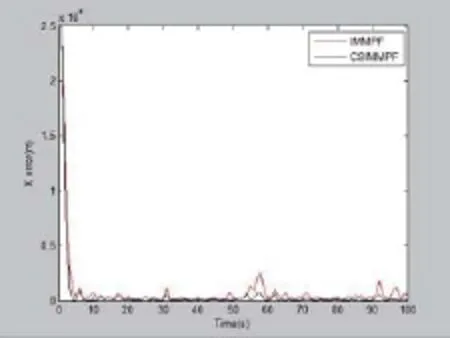
圖2 X軸方向估計均方根誤差

圖2 Y軸方向估計均方根誤差
[1]賈宇崗,梁彥,潘泉等.交互式多模型算法過渡過程的仿真分析[J].系統仿真學報,2002,14(1):16~18..
[2]劉喜貴,高恩克,范春宇.改進的交互式多模型粒子濾波跟蹤算法[J].電子與信息學報,2007,29(12):2810~2813.
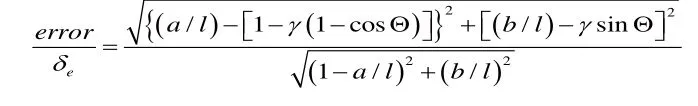
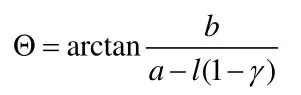
根據經驗值,γ一般取0.85。對于S型柔順仿生足機構的偽剛體模型,因所分的柔順段數較多,末端的累積誤差較大,需根據實際情況對特征半徑系數γ進行優化。通過編程計算,不斷調整相關參數值,最終優化確定的γ值約為0.59。
3.2 確定扭簧常數K
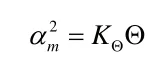
其中KΘ為扭簧的剛度系數,這種關系可用方程形式表示為

進行優化。通過編程參數尋優,最終優化確定的KΘ的值約為1.87。基于S型柔順仿生足機構的柔順段劃分及優化結果,通過對柔順段特征參數的優化,可將該柔順機構等效簡化成具有彈性變形鉸鏈的偽剛體系統,如圖5所示。
4 結語
對典型的S型柔順仿生足的特征曲線進行分段,提出根據“曲率值小則分段數少,曲率值大則分段數多”及“剛度值大則弧長變長,剛度值小則弧長變短”的方法對曲線進行分段和弧長優化,基于偽剛體模型理論,建立了典型的S型柔順仿生足機構的偽剛體模型,為進一步對其靜態和動態的分析具有重要的理論價值。

圖5 S型柔順仿生足偽剛體模型
參考文獻:
[1]王雯靜,余躍慶,王華偉.柔順機構國內外研究現狀分析[J].機械設計,2007,(06):1~4.
[2]黃則兵.柔性機構及其在仿生跳躍機構中應用的研究[J].西北工業大學碩士學位論文,2005,(04):44~48.
[3]李娜,趙鐵石,孫東波,邊輝,張建銳. 分布式全柔順機構偽剛體建模[J].機械工程學報,2010(19):17~23.
TN713
A
1671-0711(2016)11(下)-0084-03

