基于邊界積分法的V型切口尖端應力場分析

劉 劍，戴 怡

（天津職業技術師范大學數控技術與可靠性研究所，天津 300222）

基于邊界積分法的V型切口尖端應力場分析

劉 劍，戴 怡

（天津職業技術師范大學數控技術與可靠性研究所，天津 300222）

針對大靜載荷作用下V型切口尖端附近應力的相關問題，在斷裂力學已有成果的基礎上，推導了格林函數邊界單元法的基本理論及計算公式，通過采用邊界積分單元的方法，編寫和調試MATLAB程序，計算所有積分方程的解，得出V型切口邊界的應力值和較大應力值的位置。

應力；邊界積分；斷裂；V型切口

由于現實中的裂紋一般是三維的，傳統斷裂力學中“裂紋是平直”的假設不再成立，因此在三維結構中裂紋沿曲線或曲折路徑擴展成為一個棘手的力學難題。目前針對這一問題的研究多從實驗方面展開，唯象的經驗性結果占據多數，且以平面裂紋為主[1]。近幾十年來，計算機技術的發展為數值模擬奠定了基礎，有限元等計算力學方法的提出和發展也為采用數值方法解決這一難題提供了條件。

雖然有限元對彈塑性問題的分析為應力應變場的分析提供了依據，但對于三維復雜結構的應力分析，在采用有限元法求解時，應力集中區需要劃分比較密集的網格，使未知量數目增加、總體剛度矩陣帶寬變大，給求解帶來困難。此外，有限元往往是通過位移近似值來計算應力，得到的邊界應力結果一般較差，而應力集中又正好發生在邊界上，用有限元求解這類切口問題顯然不合適。邊界元法采取邊界上積分的形式，降低了問題的空間維數，將三維問題轉變為二維，從而大量減少了未知量的數目。此外，邊界元法以邊界上的量為控制對象，因而可直接得到邊界上的應力值。因此，邊界元法比有限元法更適合于求解這類應力集中問題[2-3]。本文采用邊界積分的方法求解平面V型切口的應力場，得到V型切口邊界的應力值和較大應力值的位置。

1 格林函數法邊界積分方程

1.1 邊界積分方程

平面V型切口如圖1所示。一般而言，在求解平面問題時要結合邊界條件求解平衡微分方程。對于常體力平面問題的計算，在直角坐標下的平衡微分方程為[4-5]：

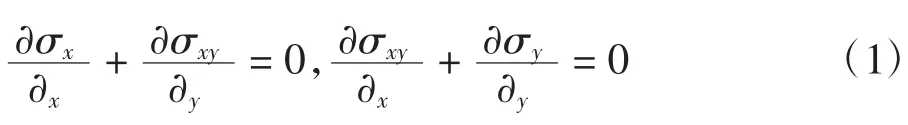
為使計算方便，將應力Airyφ（x，y）表示為：

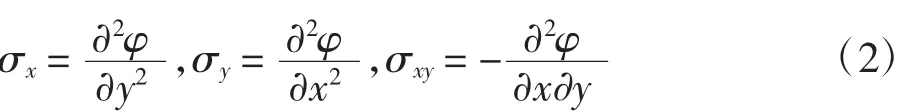
式中：φ（x，y）為應力函數；σx、σy、σxy為某一點處的應力分量。

在平面應力的計算過程中，必須滿足邊界條件，這是計算成立的基礎。邊界平面如圖1所示，所有平面邊界條件可表示為（其中q為載荷）：

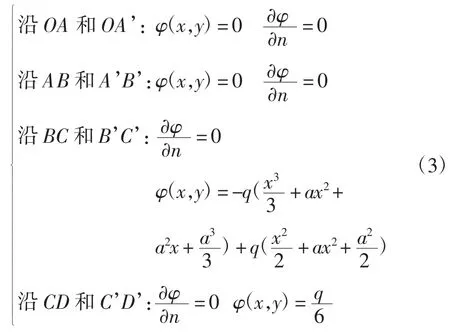
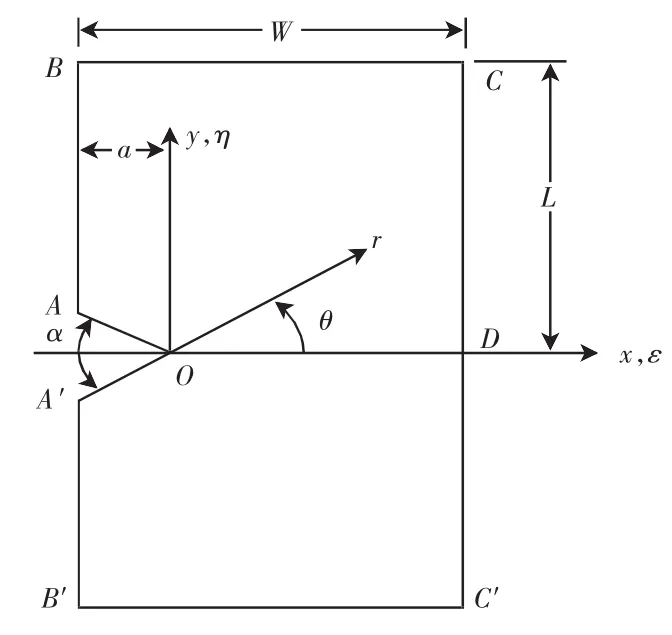
圖1 平面V型切口

采用格林函數第二方程時，方程要滿足邊界條件式（3）。單連通區域R，其邊界分為光滑曲線C、線積分方向與外法線正向，如圖2所示。

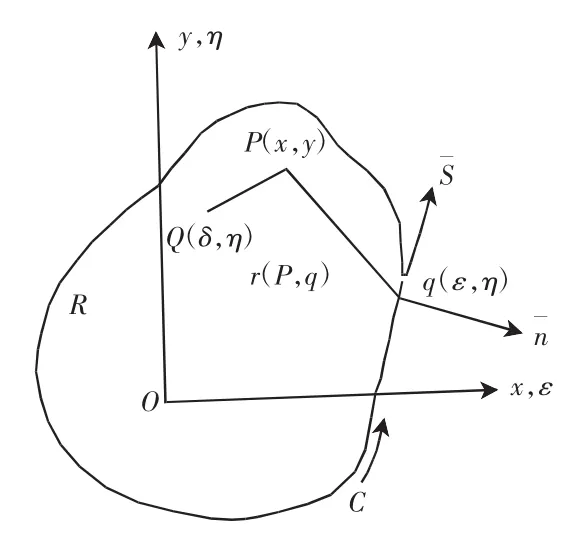
圖2 單連通區域R上的符號規定

由文獻可知，格林第二方程可表示為[6]（其中U、V為2個函數，n為外法線）：

令

將式（5）代入式（4）得：

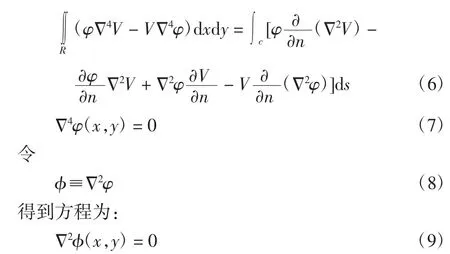
由圖2可知，令r（x，y；ε，η）為區域R上任意2點p（x，y）和q（ε，η）之間的距離，p為節點的坐標值，q為起始點的坐標。將式（5）、式（8）和式（9）代入格林方程。令V=ln r，并考慮r=0的奇異性，得到[7]：

將式（5）和式（7）與（8）聯立，取V≡P=ln r，考慮在r=0點的奇異性，得到：

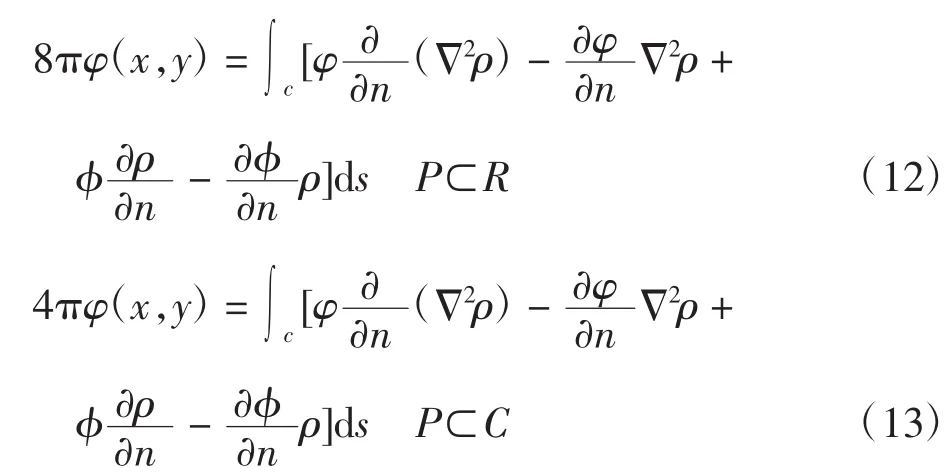
1.2 V型切口的應力方程

為方便計算，以下用撇號“′”代表法相導數。將邊界C分成n段（即n個單元）如圖3所示。在每一單元上取φ和φ′為恒定值，每一單元的中點為節點，φi和φi′即為該點上的值。

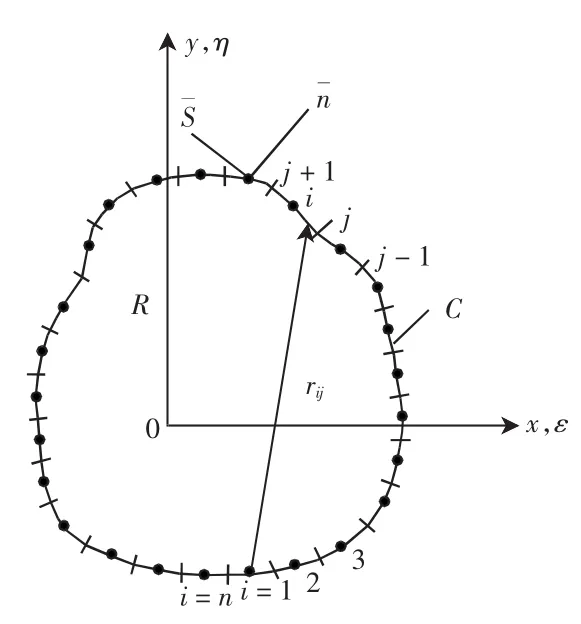
圖3 邊界C上的單元化分

由于應力函數φ在邊界BC和B’C’上并不是常數，所以φ逐段為常數的假設必然導致較大誤差。為克服這種困難，在加載邊BC和B’C’上使用直接積分取代φ[8-10]。

當i=1，2，3，…，n時，通過式（14）得到：

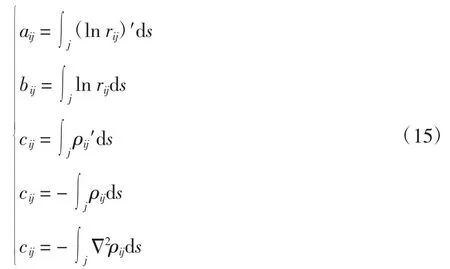
式中：rij為第i個節點到任意節點j的距離；ρij=（r2lnr）ij。當i≠j時，式（15）的系數可以采用Simpson法求出；當i=j時，式（15）的系數可以采用解析法求出。當邊界全部由直線組成時，采用解析法求出系數矩陣。式（14）可以用矩陣方程表示為[11-12]：

即歸結為：

式中：A為2n×2n階矩陣；X和R為2n×1階列矩陣。

矩陣A由平面板的幾何尺寸和邊界單元數目的分布共同確定。矩陣R依賴于應力場，即依賴于矩陣X。為通過式（12）求得應力，可不對應力函數進行微分，而直接在積分符號下進行微分；且當邊界上φ和φ′均為已知時，采用式（16）通過同樣形式的積分就可以求得所需應力。

將式（2）、式（12）和式（14）聯立求得應力方程為：

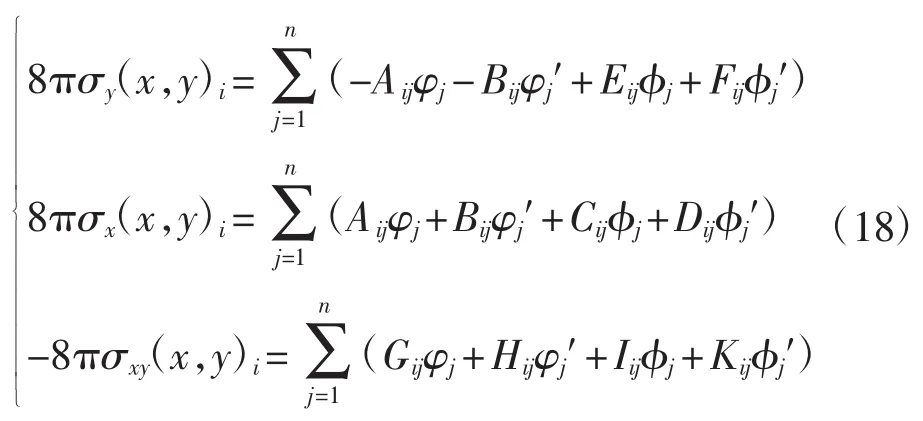
2 平面應力計算

為使計算簡便，在計算應力的過程中將應力函數、載荷及坐標均進行了無量綱化處理。使用MATLAB對平面V型切口進行劃分，如圖4所示。

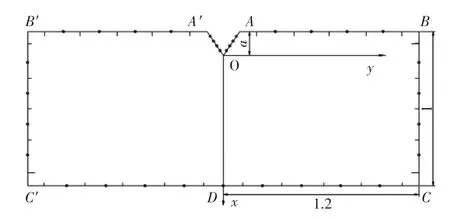
圖4 V型切口下邊界單元的劃分

由于是計算邊界節點的應力值，每個節點的應力值依次分為σx、σy、σxy進行計算。節點劃分使用平均劃分的辦法，在平面上沿邊界CD取邊界單元數序號為1～5，AB邊取單元數序號為6～10，OA邊取邊界單元數序號為11～15，BC邊取邊界單元數序號為16～20，分別對應圖4中節點的位置。通過邊界積分算法對所取的20個邊界單元進行應力計算，求得式（18）的解，計算結果如圖5至圖7所示[13-16]。

從圖5至圖7能夠得到20個邊界單元的應力值，且在3幅圖中都有一點的應力值正好為V型切口處的應力值，說明V型切口處的應力集中較大；而一般斷裂也往往發生在V型切口處，所以裂紋的危害較大。因此，研究V型切口的應力值具有實際意義，也為求取邊界應力提供了一種有效的方法。

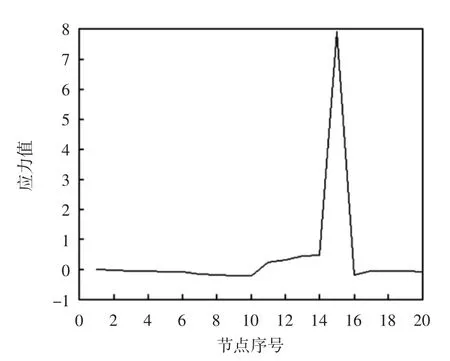
圖5 σx的應力值

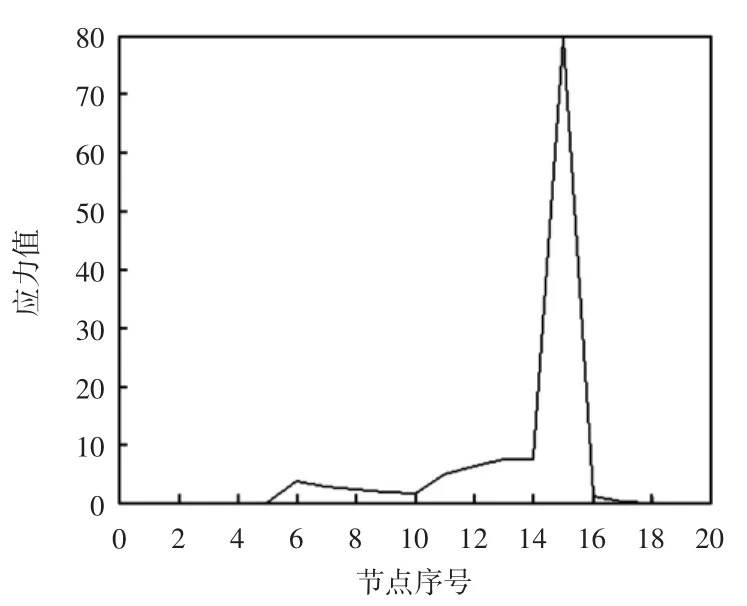
圖6 σy的應力值

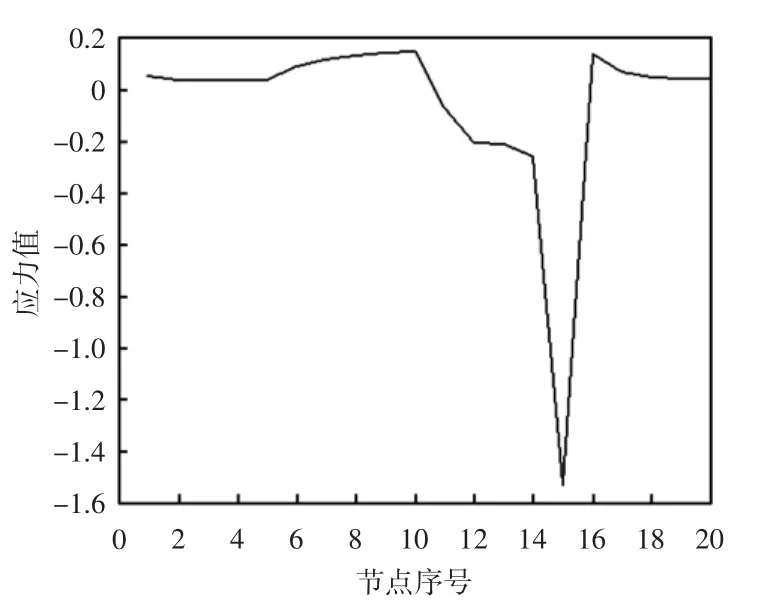
圖7 σxy的應力值

3 結束語

本文利用邊界積分的方法對平面V型切口進行應力計算，這種方法將二維積分問題轉化為一維積分問題，是一種與有限元法并列的求取應力的方法。該方法直接計算邊界上的應力值，原理直觀簡明；缺點是計算難度增大，會遇到病態矩陣，依賴計算方法的突破。當計算方法及計算手段改進時，計算結果將得到改進。隨著智能計算及大數據理論的不斷發展，邊界積分方法也將獲得進一步的完善。

［1］ 魏慶同，郎福元.機械加工中斷裂設計概念［J］.甘肅工業大學學報，1982（1）：1-19.

［2］ 魏慶同，郎福元，趙邦戟.V型切口尖端力場和位移場的冪級數解［J］.甘肅工業大學學報，1985，11（2）：10-14.

［3］ 趙邦戟，魏慶同，郎福元.三點彎曲梁的應力強度因子K1［J］.甘肅工業大學學報，1985，11（4）：28-32.

［4］ 魏慶同，郎福元，趙邦戟.I型裂紋的擴展方向及其穩定性［J］.甘肅工業大學學報，1986，12（3）：51-55.

［5］ 南京工學院數學教研組.數學物理方程與特殊函數［M］.北京：人民教育出版社，1978.

［6］ 王元淳.邊界元法基礎［M］.上海：上海交通大學出版社，1988.

［7］ 葛仁余.彈性和塑性V形切口應力奇異性分析與界面強度的擴展邊界元法研究［D］.合肥：合肥工業大學，2014.

［8］ 魏慶同，郎福元，趙邦戟.一種求解V型切口尖端應力強度因子K1的新方法［J］.甘肅工業大學學報，1986，12（4）：21-31.

［9］ MENDELSON A.Boundary-Integral Methods in Elasticity and Plasticity［Z］.NASA TN-D-7418，1973.

［10］錢文杰，王緯波，田常錄.一種V型切口應力強度因子的計算公式［J］.機械制造與自動化，2016（4）：21-23.

［11］ 曹志浩，張玉德，李瑞遐.矩陣計算與方程求根［M］.北京：高等教育出版社，1986.

［12］ 鄧勇.矩陣的滿秩分解及應用［J］.喀什師范學院學報，2015（6）：1-3.

［13］劉浩，韓晶.MATLABR2014a完全自學一本通［M］.北京：電子工業出版社，2015.

［14］趙海濱.MATLAB應用大全［M］.北京：清華大學出版社，2012.

［15］程小紅.基于MATLAB圖像簡單處理應用［J］.電腦知識與技術，2013（15）：3613-3616.

［16］ 聶影.MATLAB軟件應用研究［J］.軟件導刊，2014（7）：102-104.

Based on boundary integral method of V-shaped notch tip stress field analysis

LIU Jian，DAI Yi
（Laboratory of Reliability Engineering and Numerical Control Technology，Tianjin University of Technology and Education，Tianjin 300222，China）

As to the problem of the stress near the tip of the V-shaped notch under the action of large static load，on the basis of the results of fracture mechanics，the basic theory and calculation formula of the Green function of the boundary element method are deduced.By using the method of boundary integral unit，compiling and debugging MATLAB procedures，all solutions of the integral equation are calculated and the V cut boundary stress value and the stress of the position are obtained.

stress；boundary integral；fracture；V-shaped incision

TH114

A

2095－0926（2016）04－0036－04

2016-06-23

天津市學科領軍人才培養計劃（RC14-02）；天津職業技術師范大學科研發展基金項目（KJY12-13）.

劉 劍（1990—），男，碩士研究生；戴 怡（1962—），男，教授，博士，碩士生導師，研究方向為機電設備可靠性工程.