三角形區域上復合邊值問題探討

胡 潔，劉 華

（天津職業技術師范大學理學院，天津 300222）

三角形區域上復合邊值問題探討

胡 潔，劉 華

（天津職業技術師范大學理學院，天津 300222）

針對三角形區域上的復合邊值問題，采用問題轉化求解的辦法，研究該問題的解析解。利用Schwarz-Christoffel公式給出圓域到三角形區域的共形映射，依據橢圓函數的相關理論推導出三角形區域到圓域的逆映射；將三角形區域上的復合邊值問題轉化為圓域上的復合邊值問題，進一步通過消去法把復合邊值問題化為帶間斷系數的Hilbert邊值問題，通過解析延拓化為帶間斷系數的聯結問題，得出三角區域上復合邊值問題的解析解。

Schwarz-Christoffel公式；橢圓函數；Plemelj公式；復合邊值問題

解析函數的邊值問題是復變函數論中一個不可或缺的分支，與很多實際問題密切相關，并廣泛應用于物理學和工程技術等眾多領域。1962年路見可[1-2]首次將聯結問題（簡稱R問題）和Hilbert問題（簡稱H問題）結合，進而提出復合邊值問題（簡稱RH問題）同時給出解析解。之后，研究人員進一步討論各類邊值問題。2002年，張霞和李星[3]研究了非正則型解析函數的復合邊值問題；Guo[4]在2012年對無窮邊界上的邊值問題進行了深入研究。當然，很多固體力學、斷裂理論和平面彈性的實際問題，都可以轉化為邊值問題或奇異積分方程，而后者又與邊值問題有密切聯系，這類應用也引起學者們的重視。路見可和李星[5-6]陸續采用復分析來解決物理中的彈性力學問題。之后，李星[7]推廣了單裂縫的情況，利用Hilbert奇異積分方程得到了數值解；2001年他又討論了復分析在力學中的應用[8-9]。Begehr教授[10]也對復分析及其在力學中的應用進行了研究。近幾年，針對平面彈性的穩定性及相關特性，杜金元[11-12]也進行了進一步的研究推導。

本文研究的復合邊值問題與以往有所區別，并沒有把區域邊界只限定在Lyapunov曲線上，而是考慮在更為一般的多角形域上解決復合邊值問題。通過共形映射理論[13-14]“消去法”將其化為經典區域上帶間斷系數的Hilbert問題之后再求解，巧妙地處理特殊點的奇異性，進而得到完善的解析解。

1 RH復合邊值問題的提出與轉化

1.1 復合邊值問題的提出

設復平面上的正三角形邊界曲線為L（取逆時針方向為正），內部區域記為G。在G中有一條光滑封閉曲線Γ（取順時針方向為正），Γ內部圍成的區域記為D-，Γ和L圍成的部分記為D+，如圖1所示。

三角形區域上的復合邊值問題（記為RH問題）為：求G中一個分區全純函數Φ（z），該函數連續到邊界L上，且滿足以下邊值條件。

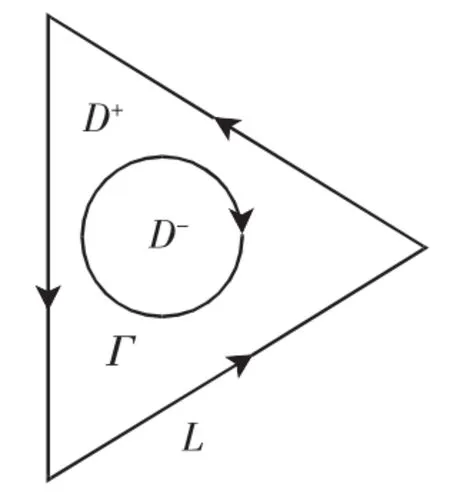
圖1 三角形區域

（1）在跳躍曲線Γ上（Φ（z）在D+和D-內全純、在L上及Γ的正負側均有極限值）滿足

式中：G（τ）、g（τ）在跳躍曲線上滿足H?lder條件，且G（τ）≠0。

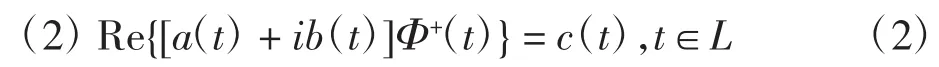
式中：a（t）、b（t）、c（t）為L上已給定的（實）函數，且都滿足H?lder條件，a2+b2≠0。

三角形的各個頂點均為L上的第一類間斷點，并要求Φ（z）在各間斷點上至多有不到一階奇異性。L上的間斷點可分為特異節點和普通節點，求解時通常要求Φ（z）屬于某個解類。這里規定在h（c0）解類中求解，即c0為某個普通節點，且Φ（z）只在c0上有界，在另外一個普通節點c1上至多有不到一階的奇異性（節點c2為特異節點）。多角形也可進行類似定義，從而將全部類型節點都討論在內（c0、c1、c2是三角形上3個頂點）。

規定指標為：

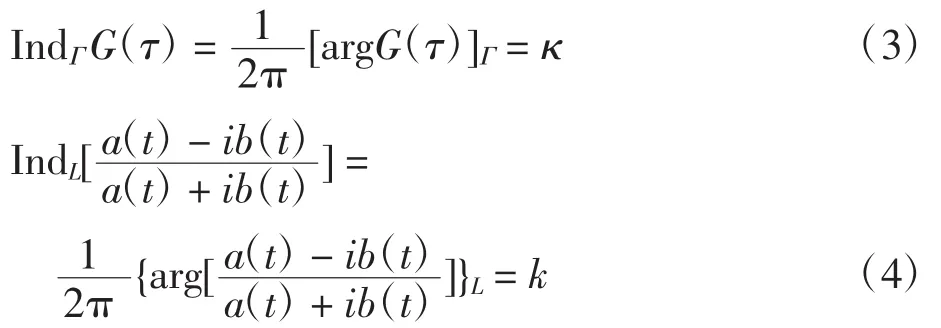
記K=2κ+k為復合邊值問題的指標，注意指標不一定是偶數。

1.2 復合邊值問題的轉化

對于三角形域上復合邊值問題，主要解決思路是通過“消去法”將其轉化為相應的H問題。構造三角形內的分區全純函數為：

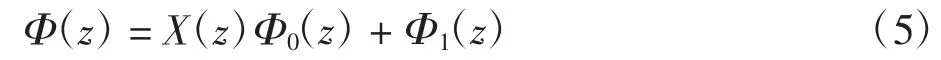
式中：Φ0（z）為G內任意連續到邊界L的全純函數；X（z）、Φ1（z）分別為滿足跳躍問題式的典則函數及一般解，在這里要求連續到邊界L。

z0為D-任意一點，得到通解為：

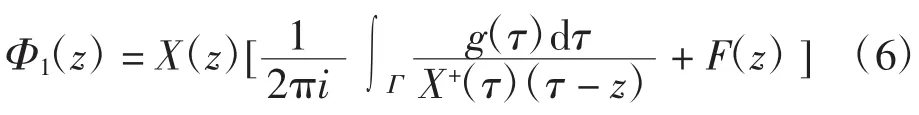
其中

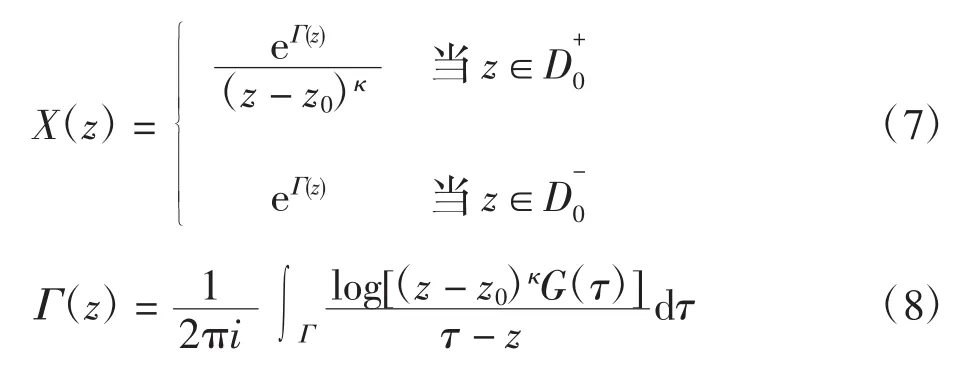
根據解析函數和典則函數的性質，容易證明：當Φ1（z）、Φ0（z）滿足上述函數條件時，Φ（z）為連續到L且滿足邊值條件式（1）的分區全純函數，反之同樣成立。將式（5）代入式（2）得到新的H問題邊值條件為：

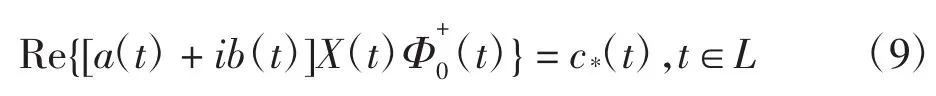
式中：c*（t）=c（t）-Re{[a（t）+ib（t）]X（t）Φ1（t）}。顯然，X（t）、c*在L上滿足H?lder條件。原RH問題轉化為G中新H邊值問題（稱新H問題為H*問題），即在G中求全純函數Φ0（z），使該函數滿足新H問題邊值條件式（9）。根據構造的式（5），消去繁瑣函數便求得Φ（z）。

2 單位圓與三角形區域之間的共形映射

通過消去法，三角形區域上RH問題轉化為H*問題，但在三角形區域上H*問題的解析解求解過程與單位圓或半平面上的情況有所不同，新的邊值條件會發生改變。針對該問題，采用三角形區域到單位圓的共形映射原理，找出共形映射的函數φ（z）的具體表達式（逆變換實現了單位圓到三角形區域的共形映射），將圓域已有的結果移植到三角形區域上并求解函數表達式。根據逆變換公式，經過二次變換得出三角形區域上H*問題的解和可解性條件公式。

2.1 Schwarz-Christoffel公式

定理1 設w=f（z）為將區域I（z）＞0共形映射到多角形區域G的單葉解析函數，x軸上的點（a1＜a2＜…＜an）依次對應到G內各個頂點（w1，w2，…，wn）。以λ1π，λ2π，…，λnπ（0＜λk＜2；k=1，2，…，n）分別表示G中w1，w2，…，wn各頂點所對應的內角，則有Schwarz-Christoffel公式為：

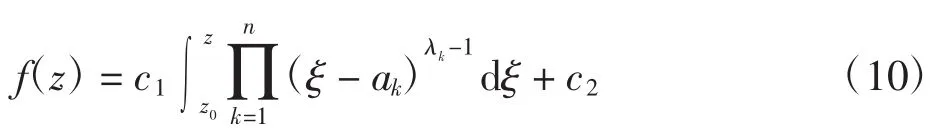
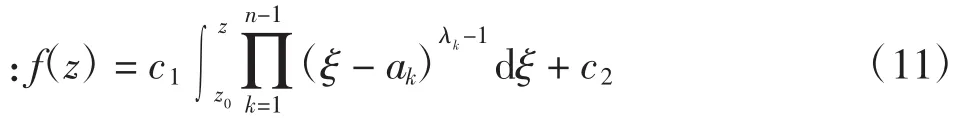
2.2 單位圓到三角形域的保形映射

由于已有半平面到多角形域為保形映射，單位圓到多角形區域的保形映射可以計算得到。這里以正三角形所圍成的單連通區域為研究對象，即可給出單位圓共形映射到三角形域的單葉解析函數表達式。

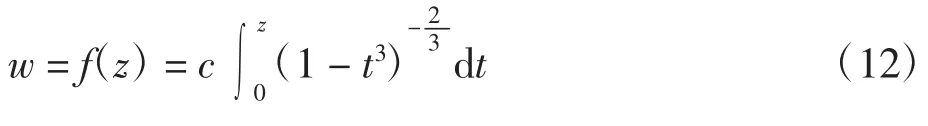
2.3 三角形區域到單位圓的保形映射

共形映射式屬于Schwarz-Christoffel積分，即橢圓積分，因此用橢圓函數理論求其逆映射。

定義1

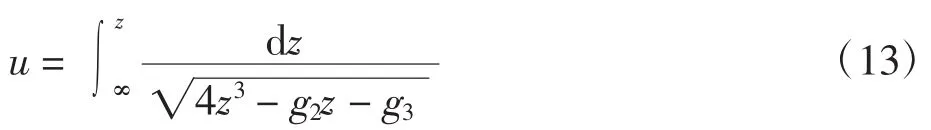
式（13）為維爾斯特拉斯式的第一類型橢圓積分，它的反函數記做z=σ（u），稱維爾斯特拉斯橢圓函數，該橢圓函數有對應的級數表達。

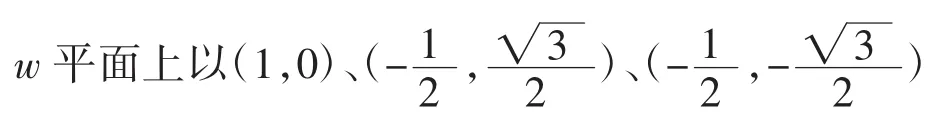
為頂點的等邊三角形內部G映射到單位圓（|z|＜1）的共形映射如圖2所示。表達式為：

圖2 三角形到圓域的映射

魏爾斯特拉斯橢圓函數的級數展開式為：

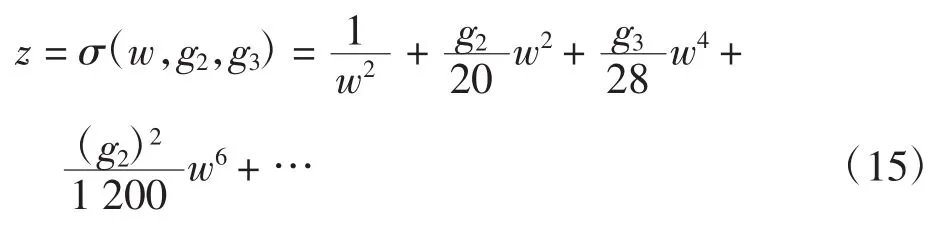
從而容易推斷出這個變換公式的二階級點為w=0、零點為w=∞。

3 單位圓域上的H*問題

在前文三角形區域與單位圓域之間共形映射的基礎上，根據單位圓上H*問題的相關結果，可得出三角形區域上的解析解和可解條件公式。但H*問題與以往閉合曲線的情況不同，是帶間斷系數的H*問題。

為表達清晰，仍延用第一節中函數符號Φ0（z）和變量t、邊值條件式（9）、單位圓邊界記號L及對間斷點的要求，但將3個頂點記號變為z0、z1、z2。式（9）中的實函數作用于共形映射t=f（v）（這里v為圓周上任意一點，t=f（v）為單位圓到三角形域的變換）之后，其形式也會變化。例如，a（t）變換為a（f（v））。為方便統一記為a（f（v））=a（t），其他實函數也如此定義，如圖3所示。

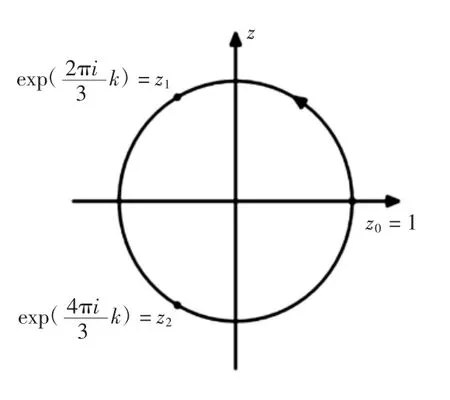
圖3 單位圓上的H*問題

求解H*問題的基本思路為：將添加一些特定的附加邊值條件的H*問題化為熟知的R問題。

3.1 指標和典則函數的說明

把Φ0（z）對稱擴張為復平面上分區全純函數，為方便仍記為Φ0（z），即在全平面內除了L上的點，處處都有

這個條件稱為附加條件。

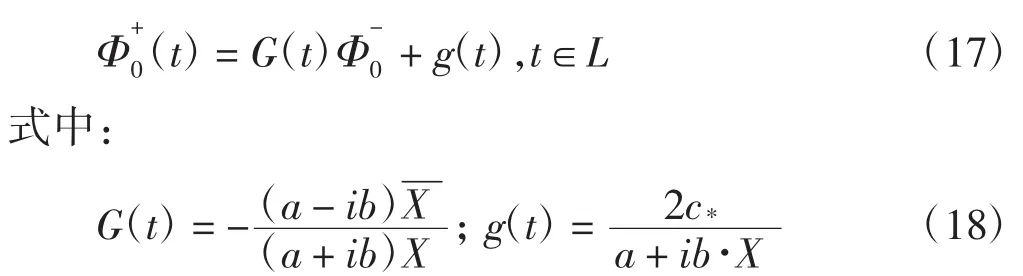
對節點進行討論。與第一節對應，z0為普通節點，且在該點處Φ0（z）有界，其他節點只要求有不到一階奇異性，3個點為G（t）、g（t）的第一類間斷點，且它們在L上都屬于H0類。

Γ（z）在L上為單值連續，IndLX（t）=-κ+IndLeΓ(z)= -κ，故R邊值問題的指標為：

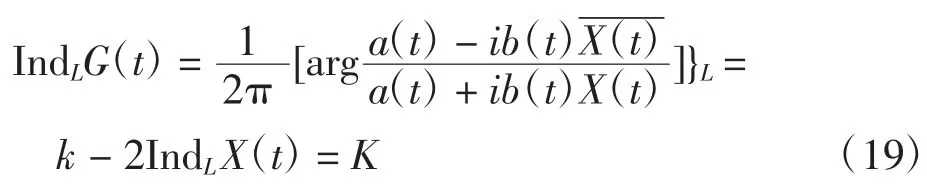
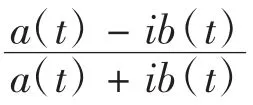
在h（z0）解類下的指標與典則函數，要根據普通節點和特異節點分布情況來定義。設由z0、z1確定的弧為L1，逆時針方向依次為L2、L3，每一個弧上任意取定l ogG（t）某一單值連續分支，，式中正負號的取值取決于在弧段中是起點還是終點。

設L1內非節點的點z*為一特異節點，易得h（z0）解類中的指標為：

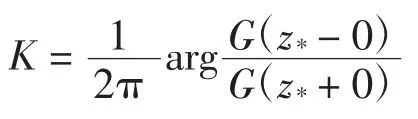
數值上與原復合邊值問題的指標相等。

相應的典則函數改寫為：

3.2 H*邊值問題的求解

（1）齊次問題（c*≡0）

①當K≥0時，相應的R0問題一般解為：

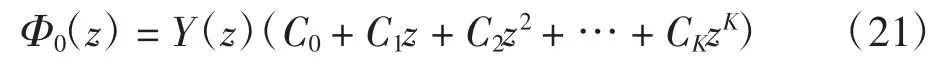
式中：C0、C1、…、CK為任意常數。

Φ0（z）要滿足附加條件，根據，得到

②當K≤-1時，只有零解。

（2）非齊次問題（c*≠0）

①當K≥0時，特解為：通解為特解式（22）加上一般解式（21）。

②當K=-1時，有唯一解，即為特解。化解為：

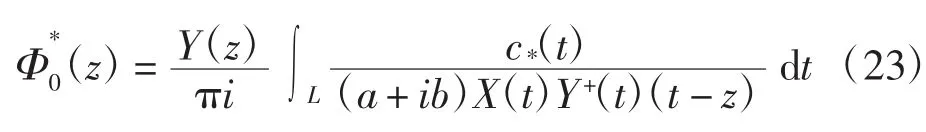
③當K≤-2時，當且僅當滿足條件

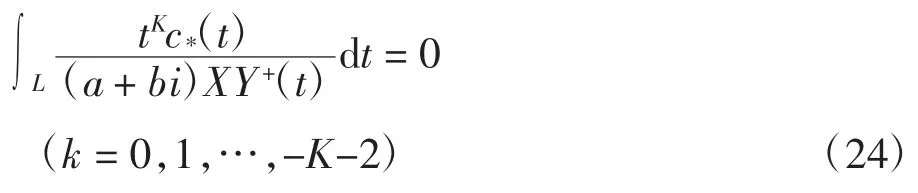
有唯一解式（23）。

3.3 原RH問題的解析解形式

單位圓上帶間斷系數H*的問題解決之后，通過單位圓到三角形區域的共形映射，易得三角形區域上對應的H*問題的解和可解條件公式。本文做了2次互逆的共形映射，最終實函數a（t）、b（t）、c（t）、c*（t）、X（t）、Γ（z）可沿用原記號。整理三角形域上帶間斷系數的RH問題的解析解形式。

（1）原RH問題中的g（τ）≡0、c（t）≠0，稱這個情況為真齊次問題。

①當K≥0時，原RH問題的一般解為：

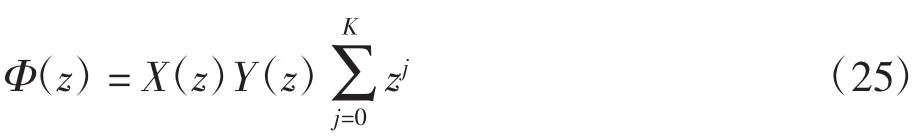
②當K＜0時，H*問題只有零解，故原RH問題也只有零解。

（2）原問題中的g（τ）≡0、c（t）=c*（t）≠0，即H*問題是非齊次的，稱真非齊次問題。

①當K≥0時，

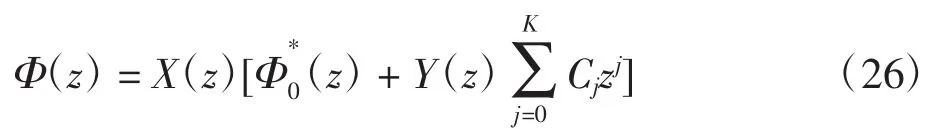
②當K＜0且條件式（24）成立時，相應R問題式（17）在R0中有唯一解，則原復合邊值問題也有唯一解式（26）。

（3）原問題中的g（τ）≠0，則Φ1（z）≠0，此時分2種情況。

2K＞0時，原RH問題一般解式（26）右邊還需加上Φ1（z）。

2K＜0時，僅當實函數滿足-2K-1個實條件時，才有唯一解，即式（26）加上Φ1（z）。

K≥0時，原RH問題的一般解為式（25）右邊加上Φ1（z）。

K＜0時，由于相應的H*問題只有零解，故原RH問題有非零唯一解Φ1（z）。

定理2（三角形區域上的RH問題）

當K≥0時，RH問題恒有解，且由K+1的實常數決定。

當K＜0時，對于真齊次問題，只有零解；對于準齊次RH問題，有非零唯一解Φ1（z）；對真非齊次RH問題，僅當已知的實函數都滿足相應的-2K-1個實條件時，才有唯一解。

4 結束語

針對單位圓域到多角形區域上的共形變換，特別以正三角形為例，采用共形映射、橢圓函數理論方法和相關數學軟件，完整求解變換的表達式。所求得的變換表達式是通用表達式，可直接應用在力學計算中。此外，還分析帶間斷點的RH問題在不同節點的求解情況，得到解決一般RH問題的常用思路，最終給出三角形區域上RH問題的解析解。整個求解思路可以移植到其他帶間斷點閉合曲線上，進而快速求解相應的RH問題。

［1］ 路見可.解析函數邊值問題教程［M］.武漢：武漢大學出版社，2009.

［2］ LU J K.On compound boundary problem［J］.Science Sinica，1965，14（11）：1545-1555.

［3］ 張霞，李星.非正則型復合邊值問題［J］.寧夏大學學報：自然科學版，2002，23（3）：193-197.

［4］ GUO D J.Multiple positive solutions for first order impulsive singular integro-differential equation on the half line［J］.Acta Mathematica Scientia：Series B，2012，32（6）：2176-2189.

［5］ 路見可.平面彈性周期問題概論［M］.武漢：武漢大學出版，2008.

［6］ 李星，路見可.雙周期彈性斷裂理論［M］.北京：科學出版社，2015.

［7］ 李星.一類周期裂紋問題的數值解［J］.寧夏大學學報：自然科學版，1998，19（1）：45-46.

［8］ LI X.Complex analytic methods in mechanics［J］.Joumal of Ningxia University：Natural Science Edition，2001，22（3）：272-273.

［9］ 李星，霍華頌，時朋朋.一維六方壓電準晶對稱條形體中共線雙半無限快速傳播裂紋的解析解［J］.固體力學學報，2014，35（2）：135-136.

［10］BEGEHR H，WEN G C.Nonlinear Elliptic Boundary Value Problems and Their Applications［M］.Harlow：Longman，1996.

［11］LIN J，DU J Y.Stability of displacement of the second fundamental problem in plane elasticity［J］.Acta Mathematica Scientia：Series B，2014，34（1）：125-140.

［12］DUAN P，DU J Y.Riemann-Hilbert characterization for main bessel polynomials with varying large negative parameters［J］. Acta Mathematica Scientia：Series B，2014，34（2）：557-567.

［13］聞國椿.共性映射與邊值問題［M］.北京：高等教育出版社，1985.

［14］普利瓦洛夫．復變函數引論［M］．閔嗣鶴，等譯.哈爾濱：哈爾濱工業大學出版社，2013.

On triangular compound boundary problem

HU Jie，LIU Hua
（School of Science，Tianjin University of Technology and Education，Tianjin 300222，China）

In view of the compound boundary value problem on the triangle region，the solution of the problem is solved by using the method of problem solving.Schwarz-Christoffel formula is used to give the conformal mapping from circular domain to triangle region，further by using elimination to change the composite boundary value problem into the Hilbert boundary value with discontinuous coefficients.By analytic continuation of the problem with discontinuous coefficients，the analytical solution of the composite boundary value problem is obtained.

schwarz-christoffel'formula；elliptical function；plemelj formula；compound boundary value problem

O175.8

A

2095－0926（2016）04－0040－05

2016-09-02

胡 潔（1991—），女，碩士研究生；劉 華（1971—），男，教授，博士，碩士生導師，研究方向為復分析及其應用.