半剛性連接石油井架的動態特性研究
劉 冬,鄒龍慶,付海龍
(1. 齊齊哈爾大學 機電工程學院,黑龍江 齊齊哈爾161006;2.東北石油大學 井架檢測國家計量認證重點實驗室,黑龍江 大慶 163318)
半剛性連接石油井架的動態特性研究
劉 冬1,2,鄒龍慶2,付海龍2
(1. 齊齊哈爾大學 機電工程學院,黑龍江 齊齊哈爾161006;2.東北石油大學 井架檢測國家計量認證重點實驗室,黑龍江 大慶 163318)
為研究焊接節點的半剛性對鉆機井架結構動態特性的影響,通過組件法計算了節點初始剛度和極限彎矩的理論值.采用雙向變剛度零長度螺旋彈簧模擬節點的半剛性,建立了半剛接井架的有限元模型并進行了自振特性和諧響應分析.與剛接井架對比表明:節點的半剛性對井架結構固有頻率影響顯著,隨著連接節點剛度的減弱,井架低階固有頻率值呈現不斷減小的趨勢,而井架側移和前傾趨勢則顯著增加,給井架安全帶來一定隱患.
半剛性;井架;動態特性 ;剛度
隨著陸地深井、超深井和海洋油氣鉆探的迅速發展,油氣田對石油井架鋼結構承載性能的要求日益提高.過去幾十年間,研究人員花費大量的精力研究鋼結構整體的強度以及穩定性等問題,并取得了許多有益的成果.但是根據長期的實踐經驗,研究者發現,鋼結構的破壞多數與局部出現損傷、腐蝕、焊接缺陷等因素有關,較少是由于結構整體強度或剛度的不足而引起的,鋼框架破壞幾乎都是從節點的破壞開始的.
石油井架屬于典型的大承載鋼架結構,主體結構是由大腿、拉筋等構件通過焊接、螺栓連接及銷座耳板連接共3種方式連接而成,其中,焊接是井架結構中主要的節點連接方式.國內學者習慣上將井架各節點間的連接假定為完全剛性連接或者理想鉸接形式,但實際上任何剛性連接都具有一定的柔性,而鉸接都具有一定的剛性[1],井架各節點間的連接應介于這兩者之間,屬于半剛性連接.近年來國內外半剛性研究多集中在平面鋼框架結構,對空間框架的研究很少,特別是對承載能力要求較高的石油井架結構,半剛性連接的研究更是寥寥無幾.
大型鉆機井架結構在承載作業時,不僅要承受提放鉆具的大鉤載荷,同時還要承受包括風載及鉆機振動產生的振動載荷等多種載荷的作用[2].本文對梁柱焊接節點的初始轉動剛度與極限彎矩進行了理論計算,以K型鉆機井架為對象,研究在動載荷的作用下,節點的半剛性對井架結構動態特性的影響,為客觀評價井架結構的抗風、抗震設計提供重要的理論基礎.
1 半剛接井架有限元模型
1.1 節點初始轉動剛度
井架主體由3~5段焊接結構組成,焊接節點在載荷作用下將承受和傳遞相當大的彎矩和剪力.假定彎矩全部通過翼緣焊縫傳遞到立柱上,且梁翼緣焊縫的受力均勻分布.焊接節點的構造如圖1所示.
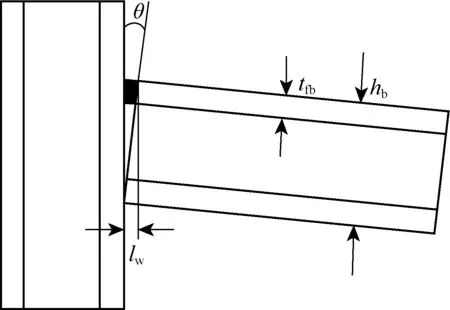
圖1 梁柱焊接節點構造示意圖Fig.1 Schematic diagram of welding joint structure
圖1中θ為節點轉角,通過組件法[3]計算焊接節點初始轉動剛度(K),如式(1)所示.
(1)
式中:Kbf、Kcf、Kpz分別為梁翼緣焊縫等效剪切剛度、梁翼緣焊縫抗彎剛度及節點域的初始剛度.
(2)
(3)
(4)
式中:hb為梁截面的高度;Δs為梁水平位移;V為節點域處的剪力;I*為翼緣焊縫慣性矩;lw為翼緣焊縫寬度;Dc為立柱截面高度;tcw為立柱腹板厚度;tfb為梁翼緣厚度;E為鋼材彈性模量;ED為焊縫彈性模量;γ為鋼材泊松比.
懸臂梁端部加載彎矩值要在極限彎矩的范圍內,極限彎矩公式采用平截面假定原則進行計算,得到平面內和平面外梁柱連接節點的極限彎矩公式如式(5)所示.
(5)
式中:Mu為節點的極限彎矩值;σs為梁翼緣焊縫的屈服強度.
1.2 半剛接井架有限元模型
JJ160/41-K型鉆機井架主體結構由大腿、拉筋和連接節點構成,大腿和拉筋均采用BEAM 189單元模擬,拉筋端部節點通過一組具有3個轉動方向的螺旋彈簧combin 39單元模擬與大腿之間的連接.節點的轉動剛度值采用式(1)及焊接節點有限元模型(如圖2所示)計算得到的數據,如表1所示,然后將節點的彎矩-轉角關系曲線賦予彈簧單元中.令每個彈簧單元的長度為零,模擬拉筋與井架大腿之間的雙向扭轉,忽略拉筋自身受扭的影響.建立半剛接井架有限元模型如圖3所示.

圖2 箱型截面大腿-拉筋焊接節點模型Fig.2 Box type welded joint model

截面形式平面內極限彎矩/(kN·m)平面內轉動剛度/(kN·m·rad-1)平面外極限彎矩/(kN·m)平面外轉動剛度/(kN·m·rad-1)大腿L260mm×130mm×5mm61.202606.090.204742.0橫拉筋L100mm×100mm×8mm7.02283.07.02244.3斜拉筋L100mm×63mm×6mm2.18130.45.03230.6

圖3 半剛接井架有限元模型Fig.3 Finite element model of semi-rigid derrick
2 半剛接井架自振特性分析
當作用在井架上的動載荷頻率與井架的某階固有頻率接近或成整數倍時,將引起井架結構的共振,這是產生井架倒塌的根本原因[4].為了研究半剛接節點對井架系統各階固有頻率和相應振型的影響,利用有限元軟件對不同連接剛度的井架結構進行自振特性分析.表2給出了不同連接剛度下井架的固有頻率值,其中K0為節點的初始轉動剛度.
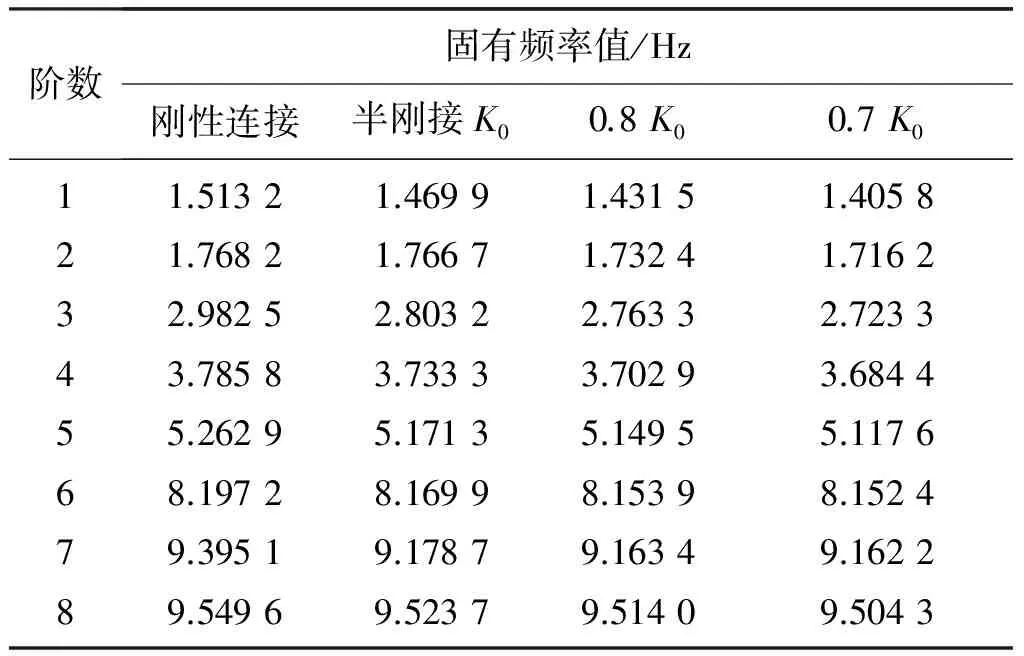
表2 不同連接剛度井架各階固有頻率值
由表2可見,JJ160/41-K型井架的基頻是1.51 Hz,半剛性連接時井架各階固有頻率值明顯小于剛性連接,伴隨著連接節點剛度的減弱,井架低階固有頻率值呈現不斷減小的趨勢,剛度的降低對高階頻率值的影響則越來越弱.井架第1階振型如圖4所示.由圖4可見,從低階模態看,剛接與半剛接井架各階的振型基本一致.在側向yz平面內發生一定的彎曲振動,整體伴有繞y軸的扭轉振動,二層臺位置表現得尤為明顯.
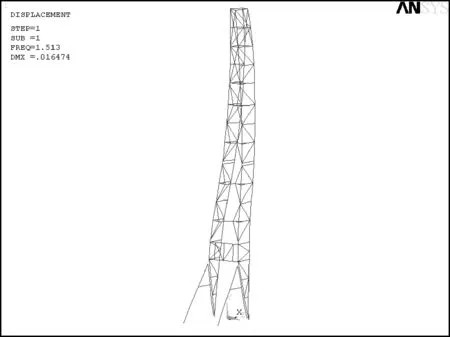
圖4 井架第1階振型Fig.4 Derrick first mode
3 半剛接井架諧響應分析
對井架結構進行諧響應分析,能夠預測結構在穩態受迫振動下對不同頻率載荷的響應特性.當鉆機井架發生卡鉆事故時鉤載達到最大設計載荷,若同時再受到動載荷的作用則井架將陷入危險工況.為了研究此時井架的動態特性是否能滿足安全要求,將最大鉤載1 600 kN平均施加在井架頂部的4個節點上,對兩種連接形式井架施加相同荷載、約束條件,分別獲得剛接與半剛性連接井架前開口頂部節點x軸方向的位移響應曲線如圖5和6所示.
井架系統的主振方向為前開口方向,1.82 Hz為井架危險工況時的主要共振頻率.由圖5和6可知,當達到共振頻率時,剛接井架的最大位移為72.021 cm,半剛接井架的最大位移達到91.358 cm.

圖5 剛接井架頂部節點頻率-位移響應曲線Fig.5 Displacement response curve of the top node for the rigid derrick

圖6 半剛接井架頂部節點頻率-位移響應曲線Fig.6 Displacement response curve of the top node for the semi-rigid derrick
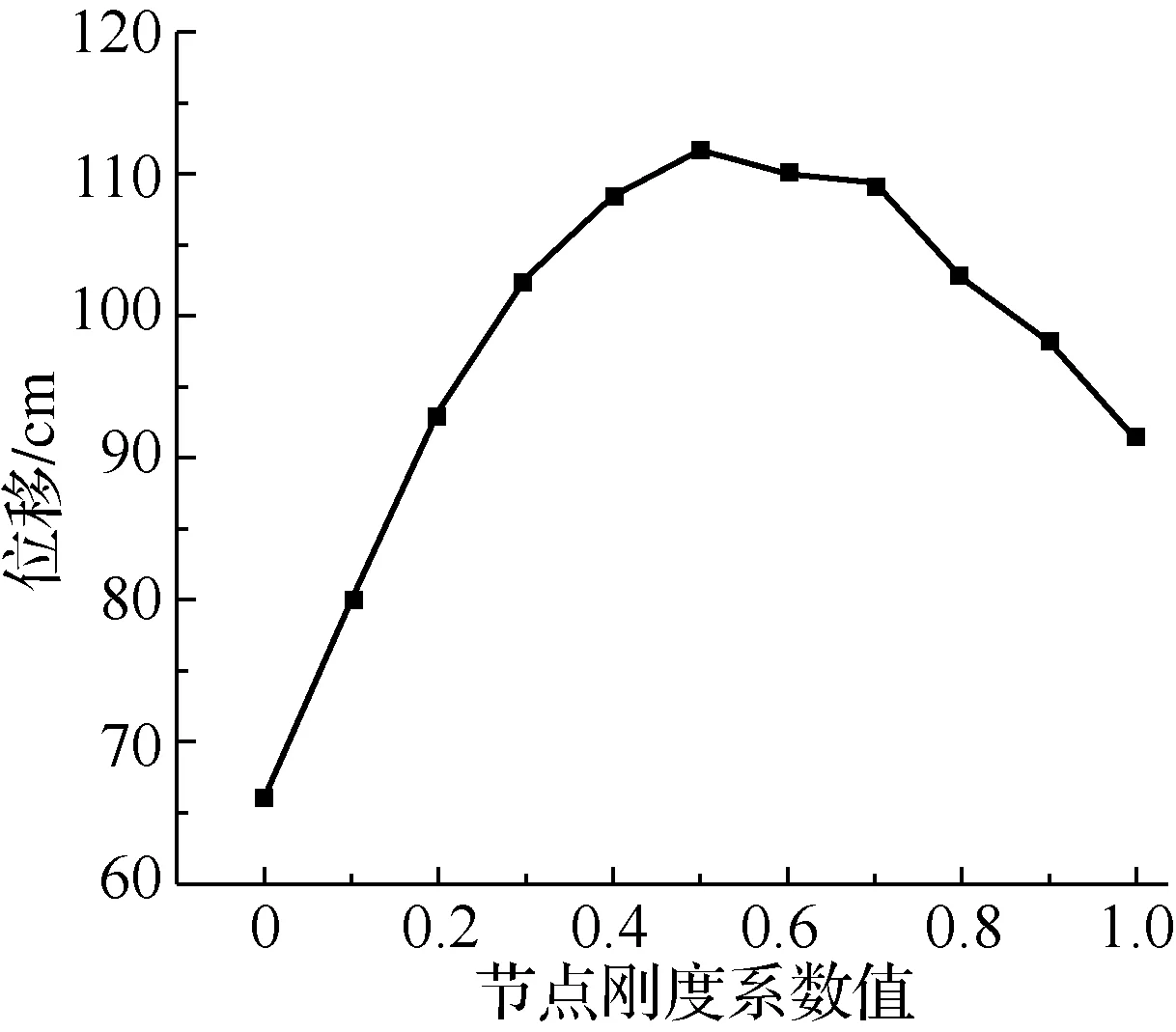
圖7 不同剛度下井架前開口頂點位移Fig.7 Displacement of the top of the derrick with different rigidity values
圖7給出了不同連接剛度下井架前開口頂點的位移.由圖7可知,在動載荷的作用下,當節點剛度在一定的范圍內下降時,半剛接井架的最大位移響應有增大的趨勢.說明半剛接節點的存在會增大井架側移和前傾趨勢,在后期振動中表現得更加明顯.這是由于半剛接節點具有一定的轉動自由度,結構具有較好的延性和耗能能力,半剛接井架的塑性變形能力要強于剛性連接井架,將更有利于抵抗動載荷的作用[5],但同時也使井架穩定安全系數降低,位移的增大易引發井架失穩倒塌事故.
當節點的剛度降到一定值以后,最大位移響應又有不斷減小的趨勢,其共振頻率對應的位移值并不一定大于剛接井架.節點的剛度變化對井架結構的動力響應的影響沒有特定的規律,這與靜力分析中位移與結構的剛度總是成反比不同,動力分析中響應和剛度關系更為復雜[6].
4 有限元模型的試驗驗證
井架振動測試儀器由TS3828型動態應變儀、UT3232S型數據采集器、UTekl型軟件包及筆記本電腦組成,分別對井架進行動態載荷測試和模態參數測試.動態載荷測試采用BJ115-10AA型應變計布置在井架每根大腿的上下層兩處位置. 共有32個測點;模態測試采用TS1102/1100型加速度傳感器布置在井架大腿上中下5處位置.井架的結構簡圖及應變計和傳感器的具體布置方案如圖8和9所示.
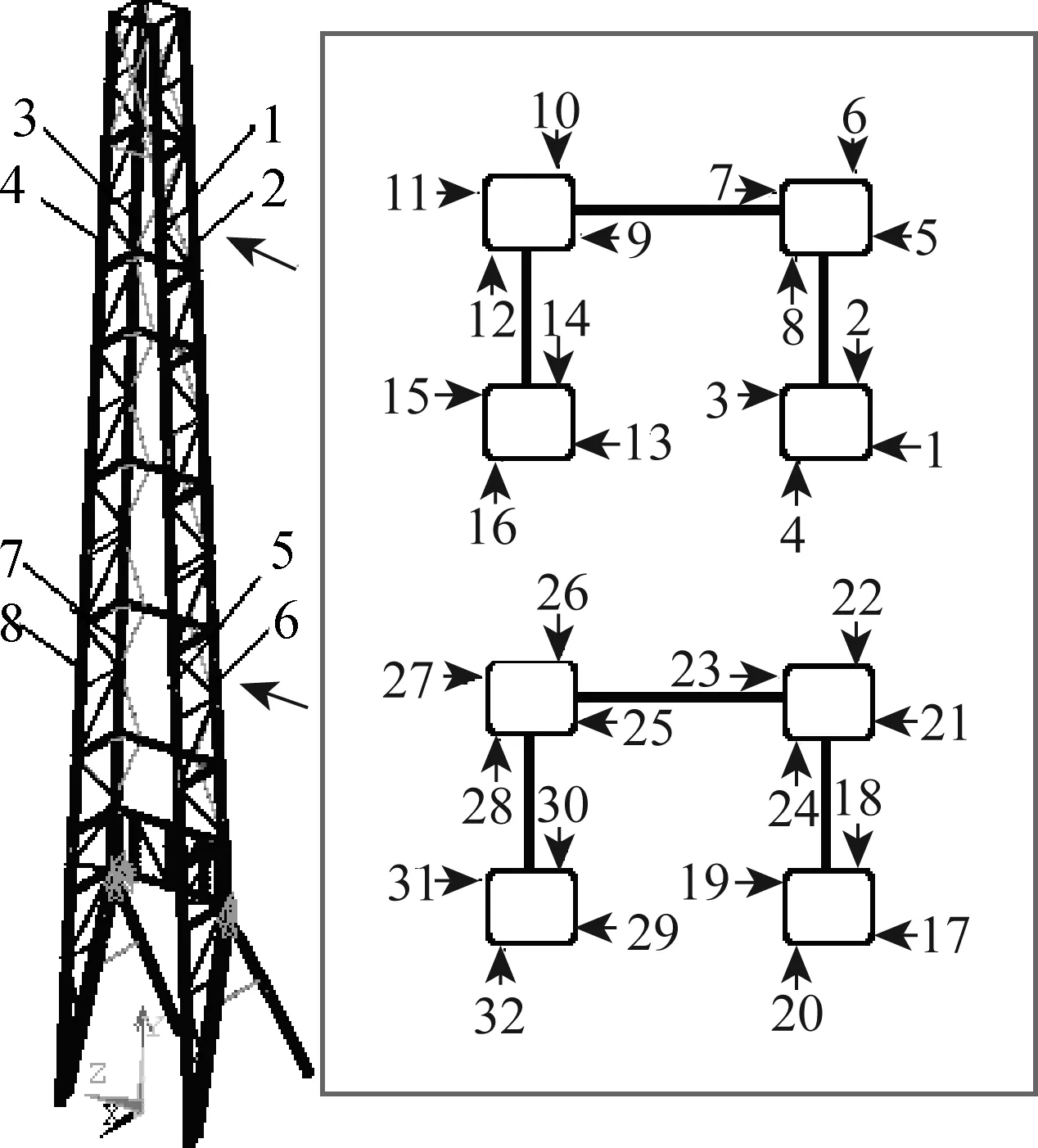
圖8 井架動載測試應變計布置方案Fig.8 Arrangement scheme of dynamic load test for derrick

圖9 井架模態測試傳感器布置方案Fig.9 Arrangement scheme of modal test for derrick
對井架動載測試得到的多組數據曲線進行分析,通過轉換得到最大應力和應變值.為驗證半剛接井架有限元模型的準確性,通過測試數據與有限元仿真結果的對比進行判斷.在測試鉤載為56.84 kN下,井架1~8號大腿處測試應力和模擬應力結果的對比如表3所示.

表3 測試應力及仿真模擬應力值
由表3可知,井架動載測試與仿真試驗結果的擬合相對誤差均在5%以內,從靜力學方面驗證了所建立的半剛接井架有限元模型的準確性.對井架進行模態參數測試[7],識別得到該鉆機井架的一階固有頻率為1.438 Hz,與半剛性連接時井架一階固有頻率值非常接近,從動力學方面也驗證了該井架模型的正確性.振動測試結果與仿真試驗結果對比表明,實際工況下,井架各節點間處于半剛性連接狀態,用組件法計算得到的節點剛度和極限彎矩值是合理的,模擬井架半剛性連接的方法是可行的,與現場真實井架結構基本一致.利用半剛接井架有限元模型進行的靜、動力相關的計算,所得的結論具有一定的參考價值.
5 結 論
(1) 半剛性連接分析中,彎矩-轉角關系最能反映連接變形與荷載之間性能.用螺旋彈簧來模擬節點柔性對梁單元的影響,通過組件法推導了井架大腿與拉筋之間的焊接節點初始剛度的理論計算公式,獲得了節點彎矩-轉角關系.
(2) 通過對不同連接剛度井架結構的自振特性分析表明,節點的半剛性對井架結構的固有頻率影響顯著.隨著節點剛度的降低,井架結構的低階固有頻率呈現不斷減小的趨勢,剛度的降低對高階頻率值的影響則越來越弱.因此,將井架按照剛接結構進行設計將造成較大的安全隱患,必需考慮到節點的柔性對其結構動力特性的影響.
(3) 在持續周期性簡諧載荷作用下,節點轉動剛度在一定的范圍內降低時,會增加井架結構的側移和前傾趨勢,嚴重的將引起井架失穩倒塌;當節點的轉動剛度降到一定值以后,半剛性連接井架的共振頻率對應的位移值并不一定大于剛接井架.因此對于鉆機井架安全評定時,焊接節點半剛性的影響不容忽視,同時還要考慮動載荷的具體種類、激勵形式、結構本身特性等多重因素的影響,為油田作業安全生產提供可靠的理論依據.
[1] 舒興平,袁智深,張再華,等.半剛性連接鋼結構理論與設計研究的綜述[J].工業建筑,2009,39(6):13-21.
[2] 鄒龍慶.石油鉆機井架動態響應分析[D].哈爾濱:哈爾濱工程大學船舶工程學院,2006.
[3] 鄒龍慶,劉冬,崔曉華.石油井架結構焊接節點的剛度計算[J].石油礦場機械,2012,41(2):17-20.
[4] 趙煥娟,齊明俠,趙娜.鉆機井架可靠性分析[J].石油礦場機械,2010,39(3):22-27.
[5] HONG K,YANG J G,LEE S K. Parametric study of double ang1e framing connections subjected to shear and tension [J].Journal of Constructional Steel Research,2001,57(6): 997-1013.
[6] 孫修禮,王永明,管毅,等.半剛性連接框架結構的動力響應分析[J].工程抗震與加固改造,2007,29(4):18-22.
[7] 劉金梅.在役鉆機井架使用安全性綜合評價方法研究[D].大慶:東北石油大學機械科學與工程學院,2012.
Study on the Dynamic Response of Oil Derrick Structure with Semi-rigid Joints
LIUDong1, 2,ZOULong-qing2,FUHai-long2
(1. School of Mechanical and Electronic Engineering, Qiqihar University, Qiqihar 161006,China;2. State Key Laboratory of Metrological Authentication for Petroleum Drilling Derrick,Northeast Petroleum University,Daqing 163318,China)
In order to study the influence of semi-rigid joints on the dynamic characteristics of the mine derrick structure, the theoretical calculation formula of the stiffness and ultimate moment of the welded joint between the derrick and the joints are obtained by the component algorithm. The zero-length spiral spring with dual direction and variable stiffness is applied to simulate the semi-rigid joints, the finite element model of semi-rigid derrick is established, the harmonic response analysis and the natural vibration characteristics are carried out. By comparing with the rigid connection, semi-rigid joints have a significant effect on the natural frequency of the derrick structure. With the decrease of the stiffness of the joints, the natural frequency of the derrick structure decreases and the derrick lateral displacement and the forward tendency significantly increase, which bring some safe trouble to the derrick.
semi-rigid; derrick; dynamic characteristics; stiffness
1671-0444 (2016)04-0518-05
2015-12-21
國家科技支撐計劃資助項目(2012BAH28F00);黑龍江省自然科學基金資助項目(E201409);齊齊哈爾大學教育科學研究資助項目(2015054)
劉 冬(1986—),男,黑龍江大慶人,講師,博士研究生,研究方向為大型鋼結構的設計、承載能力與檢測以及安全評定工作. E-mail: liudong224@126.com
TE 923
A

