正交非線性滲流定理

齊成偉

（重慶科技學院-石油與天然氣工程學院，重慶 401331）

正交非線性滲流定理

齊成偉

（重慶科技學院-石油與天然氣工程學院，重慶 401331）

將“正交冪比方程”代入不可壓縮流體穩定滲流連續方程后得到了“正交低速非線性滲流控制方程”。正交低速非線性滲流控制方程是二階非線性偏微分方程，故除“直流場”外，其符號解極難求得。綜合運用場論和微分幾何知識，對流場幾何進行了定性分析，得到“正交非線性滲流定理：假設非線性滲流的等壓面與流線正交，若流場為‘曲流場’，則相同條件下單相不可壓縮或可壓縮流體非線性滲流與單相不可壓縮流體線性滲流的流線形狀不同。進而，等壓面形狀亦不同。”以斯托克斯流動為類比，指出了非線性滲流的等壓面與流線的不正交可能性。

滲流力學 流場幾何 正交冪比連續方程 曲流場 流線曲率矢量公式 引理 復曲率公式 廣密壓裂

0 引言

如果油水地下滲流具有“低速非線性”，那么相同條件下的低速非線性滲流與線性滲流有何不同呢？

1 本構方程

描寫低速非線性滲流之平行流的冪比方程［1］為：

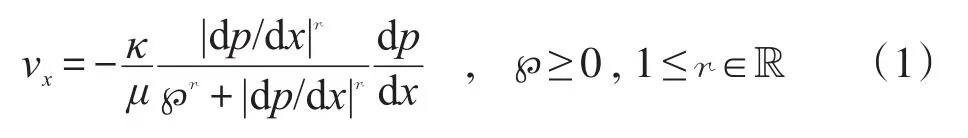
式中，v為流體滲流速率，m/s；κ為多孔介質滲透系數，m2；μ為流體動力黏度，Pa·s；p為流體壓強，Pa；x（y、z）為Descartes坐標系的橫（縱、豎）坐標（作為角標，示意方向），m；r為非線性指數，無量綱；?為漸近線截距，Pa/m。

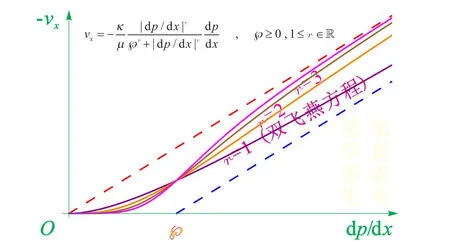
圖1 低速非線性滲流本構方程

如圖1所示：r控制vx～dp/dx曲線的形狀；控制vx～dp/dx曲線的大小。

巖心滲流測試采用的圓管巖心夾持器或填砂圓管限定流動為平行流，或稱一維流。無論是線性滲流還是非線性滲流，平行流的等壓面與流線必然正交。對于線性滲流，二維流、三維流的等壓面與流線正交。對于非線性滲流，除“柱徑流”外的二維流、除“球徑流”外的三維流的等壓面與流線也一定正交嗎？未經實驗，不得而知。

假設低速非線性滲流的等壓面與流線正交，則其滲流速度與壓強梯度之間的本構關系可寫為“正交冪比方程”。分量形式的正交冪比方程為：

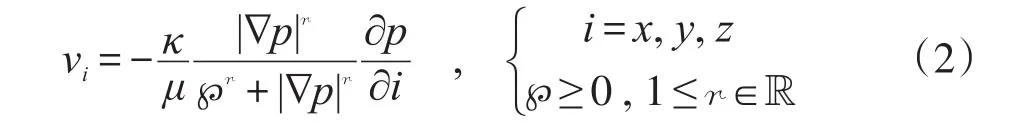
矢量形式的正交冪比方程為：

2 控制方程

將式（3）代入不可壓縮流體穩定滲流連續方程

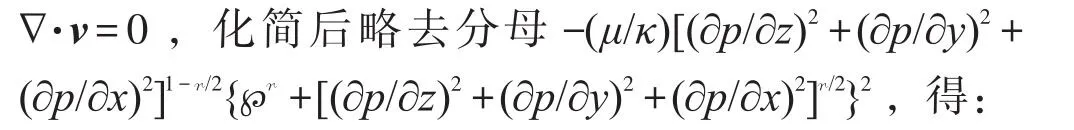
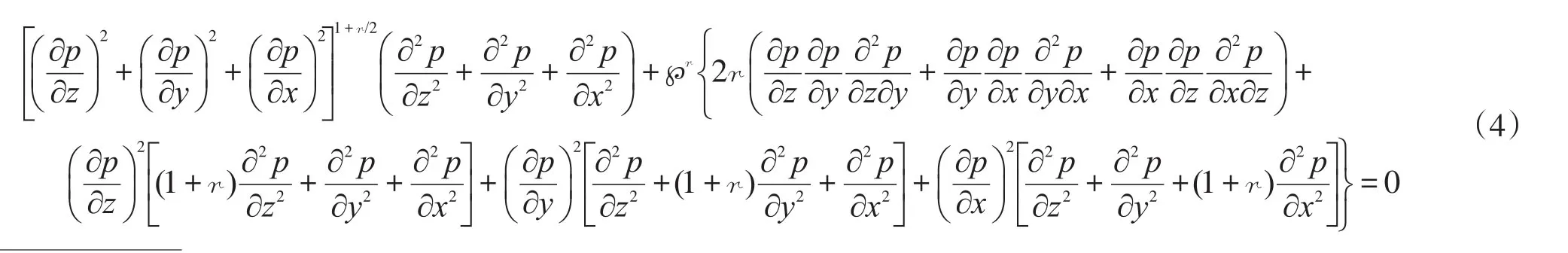
稱式（4）為“正交冪比連續方程”或“正交低速非線性滲流控制方程”。讀者可以驗證：r=1情況下的平行流壓強函數p=[qμ/(4κw)]{1+[1+8κw?/(|q|μ)]1/2}|x|（q為裂縫匯（或源）強度，m2/s；w為帶形地層寬度，m）、柱徑流壓強函數（文獻［1］式（4），[]內的q替換為|q|，q為二維點匯（或源）強度，m2/s）和球徑流壓強函數（文獻［1］式（6），[]內的Q替換為|Q|，Q為三維點匯（或源）強度，m3/s）是方程（4）的符號解。

3 滲流場論

3.1 渦矢量場

為了普適性，將正交非線性滲流本構方程寫為：

式中，g()為可微函數；g(|?p|)為非線性系數函數，無量綱。強令g()=1，則式（5）退化為線性滲流本構方程，即Darcy's law。式（5）囊括Forchheimer's law。

正交非線性滲流渦矢量場為：

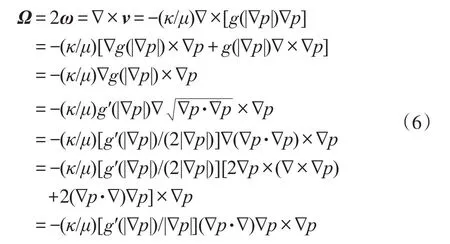
式中，Ω為滲流渦矢量，s-1；ω為滲流角速度，rad/s。

式（6）中，(?p·?)?p×?p的Descartes坐標形式為：

3.2 流線曲率矢量場

記流線函數為：

將式（8）轉化為參數方程形式，如：

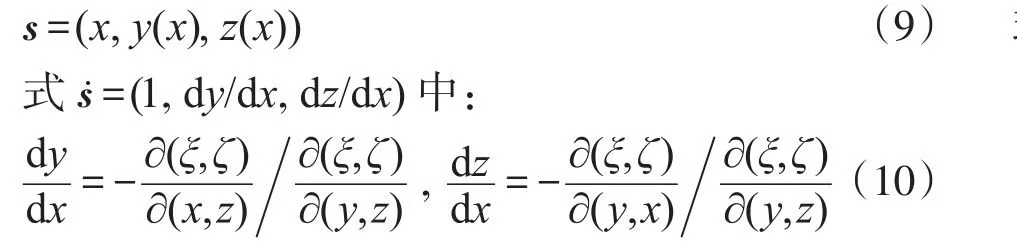
式（5）與v=(CⅠ/ρ相結合，得：

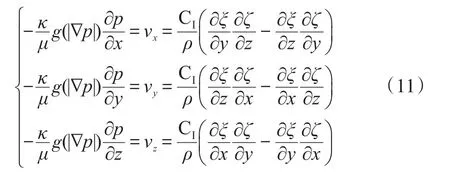
式中，ρ為流體質量密度，Kg/m3。

將式（11）代入式（10），得：

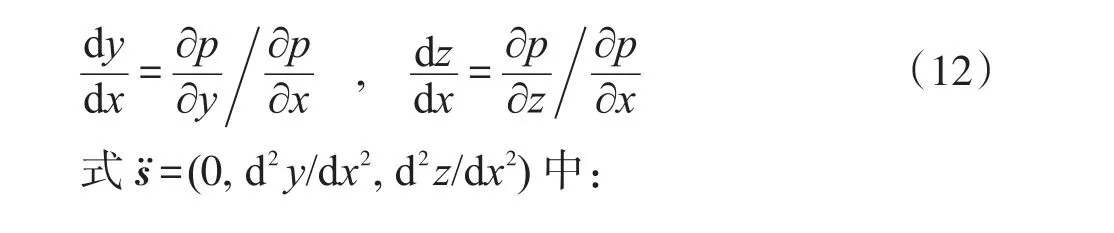
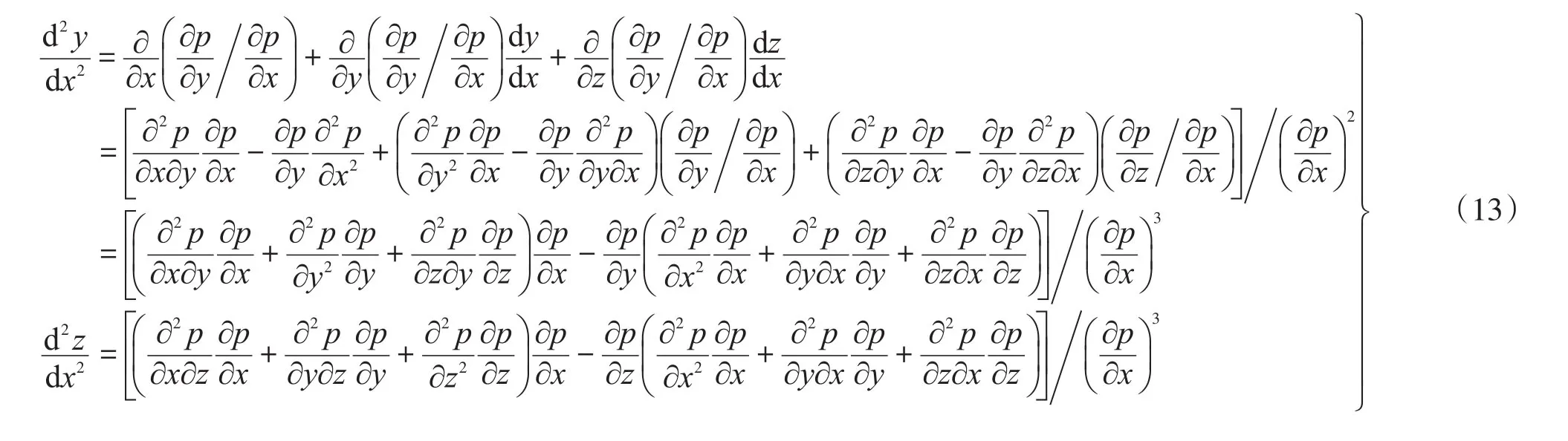
對比式（13）與式（7），知：

據式（14）、式（12）、式（7）、式（6），知流線曲率矢量場為：

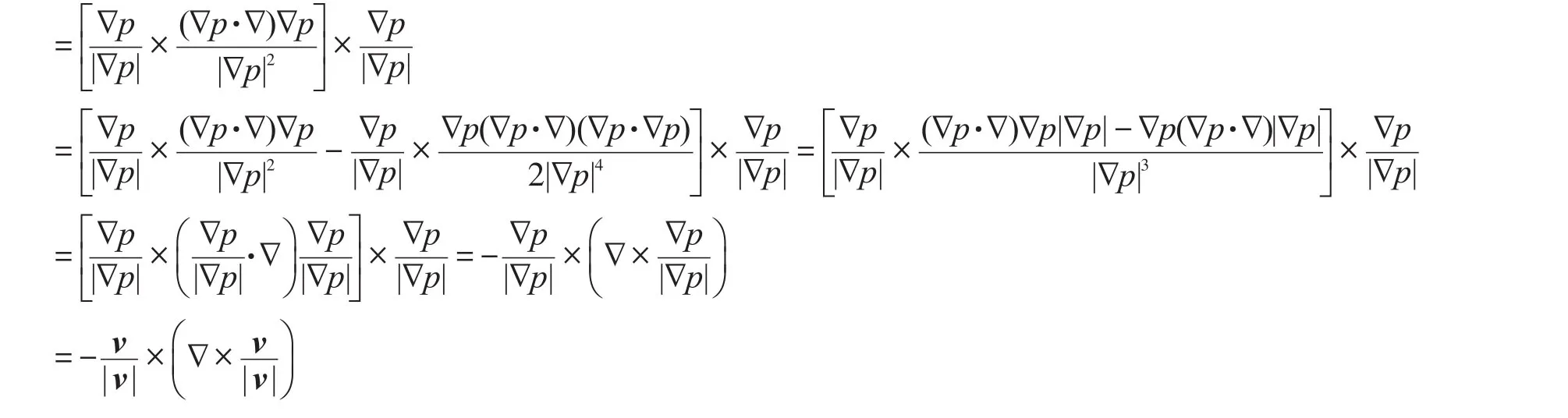
式中，kξ∩ζ為流線曲率矢量，m-1。

式（15）倒數第2行顯示：正交非線性滲流的流線曲率矢量是歸一化壓強梯度與其旋度的負矢積。

式（16）顯示：除平行流、柱徑流和球徑流（下稱“直流場”，）外（下稱“曲流場”，，式（5）所描述的滲流速度場為有旋場。

引理：正交非線性滲流之直流速度場為無旋場；正交非線性滲流之曲流速度場為有旋場。

3.3 平面勢流流線曲率

敬請讀者欣賞無限大等厚均質各向同性水平地層內環形裂縫群激發的線性滲流場的流線曲率絕對值密度圖。

對于二維問題，式（7）退化為：

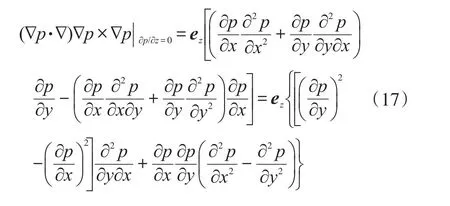
記平面穩態流速場復位勢與復坐標的函數關系為：

式中，f()為解析函數；φ為勢，m2/s；ψ為流，m2/s。對于滲流場，φ=κp/μ。注意：解析=共形。

根據Cauchy-Riemann條件［2］，知：

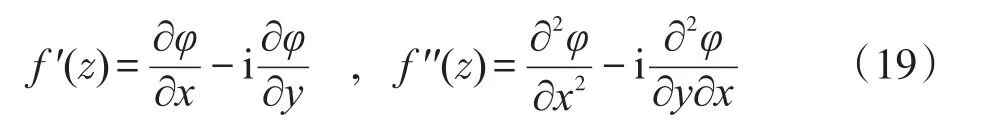
顯然，用式（19）湊出式（17）的{}部分是可能的。嘗試后發現：

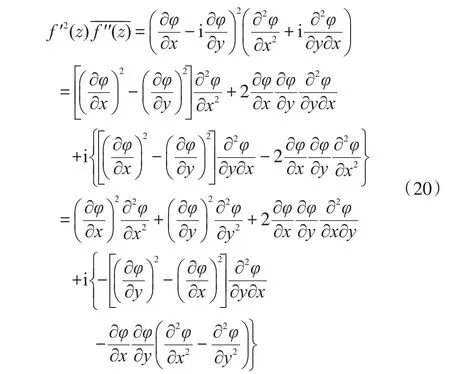
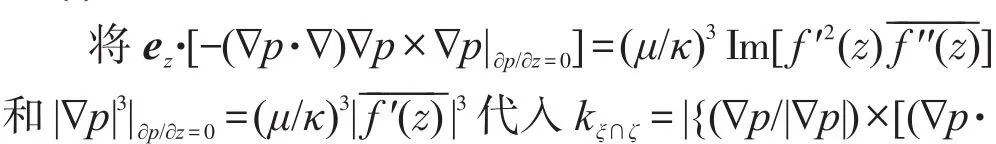
可將式（21）改寫為：

式（22）規定：流線向左偏轉，流線曲率為負；流線向右偏轉，流線曲率為正。

非常幸運，平面勢流等勢線曲率恰為：

可將kφ+ikψ稱為“平面勢流‘復曲率’”，記為k，譯為“complex curvature”。于是，復曲率公式為：環形裂縫群復勢通式［3］為：

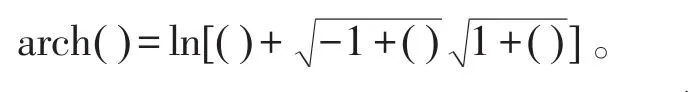
將式（25）代入式（24）后做替換z→x+iy，得：

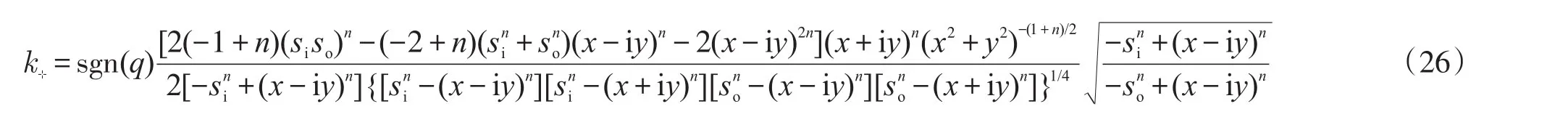
令si/so=1/3，根據式（26）繪得等勢線曲率密度圖（向?花）和流線曲率絕對值密度圖（背?花），見圖2。

圖2 環形裂縫群線性滲流復曲率密度圖

4 流線形狀

假設流場邊界形狀相同且流入流出端面皆為等壓面的均質各向同性多孔介質內單相不可壓縮或可壓縮流體非線性滲流與單相不可壓縮流體線性滲流的流線形狀相同，或稱流線重合，則同一坐標點處的滲流速度方向一致，即：

式中，角標n-l、l依序示意非線性滲流、線性滲流。

將質流密度ρn-lvn-l,ρlvl代入散度定理，得：

式中，m。為流場內某一口井或某幾口井的質量流量，Kg/s；V為僅包含該口井或該數口井的任一控制體的體積（作為下標，表示積分區），m3；S為相應的控制面的面積（作為下標，表示積分域），m2；n^為控制面上的單位外法矢量，無量綱。

式（29）與式（27）相結合，得：

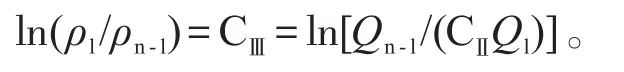
對于單相可壓縮流體非線性滲流與單相不可壓縮流體線性滲流而言，ln(ρl/ρn-l)≠CⅢ。將正壓條件ρn-l=ρn-l(x,y,z)=?n-l(pn-l)代入式（31）后再結合式（5），得：

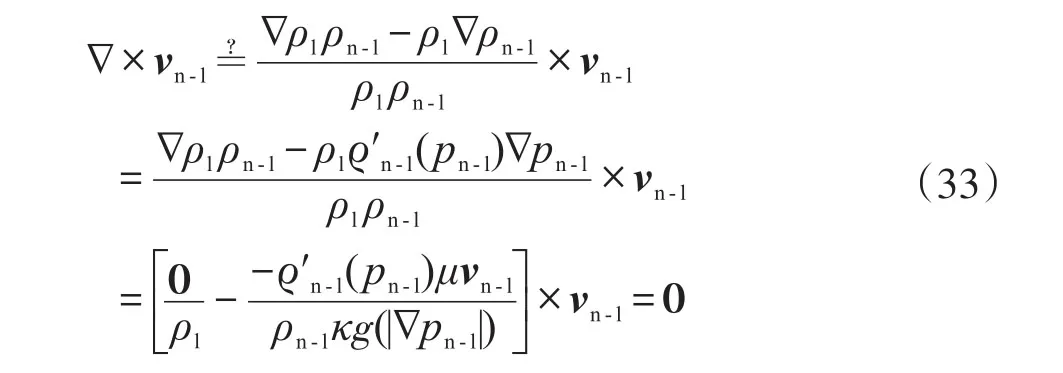
然而，式（16）顯示，對于曲流場，有：

綜上，對于相同條件下的曲流場，式（32）、式（33）與式（34）或式（16）矛盾，故式（27）所表述的“流線重合假設”與引理矛盾。因而，對于曲流場，流線重合假設不成立，即“若

正交非線性滲流定理：假設非線性滲流的等壓面與流線正交，若流場為曲流場，則相同條件下單相不可壓縮或可壓縮流體非線性滲流與單相不可壓縮流體線性滲流的流線形狀不同。進而，等壓面形狀亦不同。

5 緣何正交

流體力學里的不可壓縮Perfect fluid“繞球無旋層流”和不可壓縮Newtonian fluid“繞球有旋層流”或可帶來啟示。下面回顧原點處半徑為r的小球對流速場v∞=v∞ex的影響。此處，v表示真實流動速度。對于單相不可壓縮流體，ρ為實正常數，故不妨令CⅠ=ρ。

5.1 繞球無旋層流

無旋場必是有勢場。線性流動與線性滲流具有相同的控制方程，即?2φ=0。對于無多孔介質的流動，φ≠κp/μ。因已忽略重力，故等勢面與等壓面重合。

結合邊界條件求方程?2φ=0的符號解，取ζ=arc tan(z/y)后結合ξ(x,0,0)=0求方程-?φ=v=?ξ×?ζ的符號解，得繞球無旋層流的勢函數和流線函數：

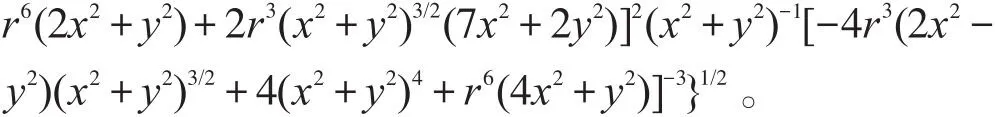
根據式（35）繪得繞球無旋層流流網圖，見圖3。

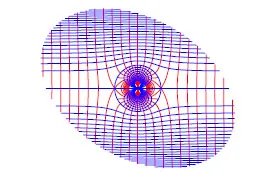
圖3 繞球無旋層流流網縱對稱面圖

如圖3所示：前駐點［4］(-r,0,0)和后駐點(r,0,0)外的空間內，繞球無旋層流的等勢面與流線處處正交。

5.2 繞球有旋層流

本文僅重述Stokes flow，而不重述Oseen flow。

不可壓縮Newtonian fluid的Stokes equations為：

結合邊界條件求方程組（36）的符號解，得繞球有旋層流的壓強場函數和速度場函數：

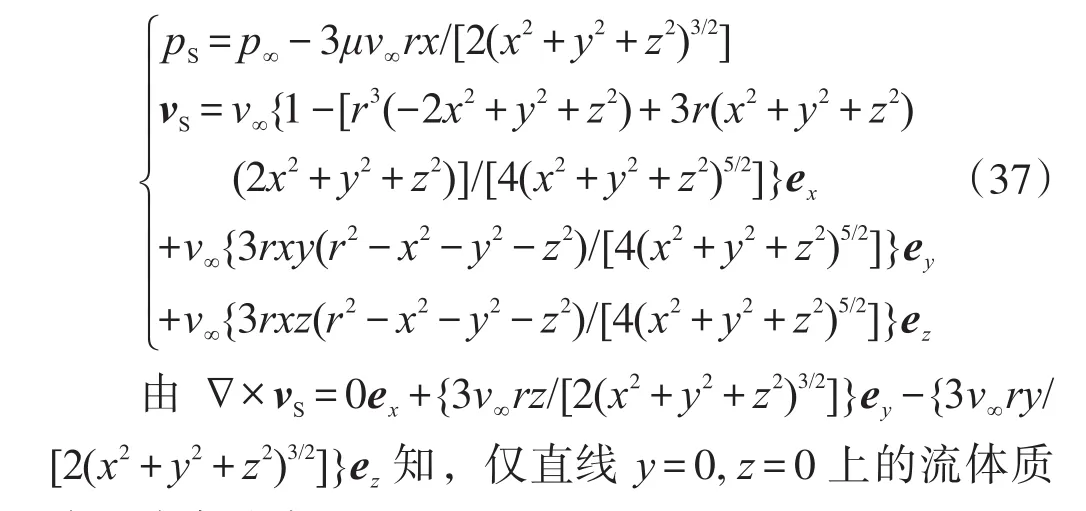
點沒有角速度。

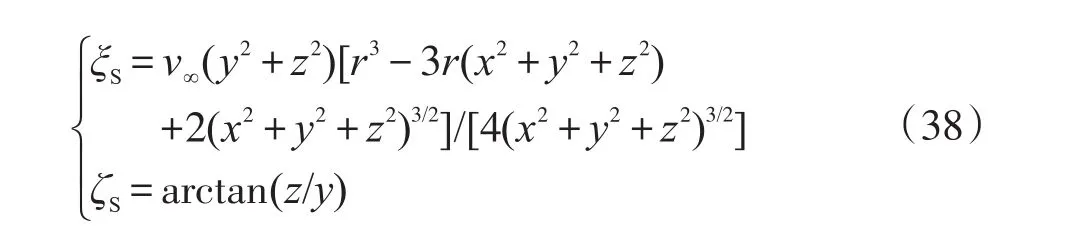
根據式（37）和式（38）繪得繞球有旋層流流場圖，見圖4。注意觀察：球外曲流線兩次斜穿同一等壓面。

圖4 繞球有旋層流流場縱對稱面圖

等壓面與流線正交的數學條件為?pS×vS=0。因為

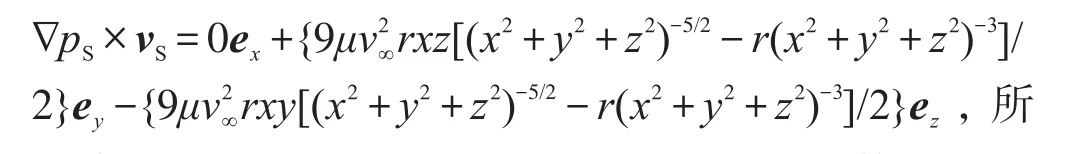
以直線y=0,z=0和平面x=0外的空間內等壓面與流線處處不正交。

6 結束語

正交非線性滲流定理表明：無限大等厚均質各向同性水平地層內具有無限導流能力且鉛垂貫穿地層的有限長無寬直裂縫激發的正交非線性滲流場的流線不是以裂縫端線等高點為焦點的雙曲線，等壓面也不是以裂縫端線為焦線的橢圓柱面。擬共形？

非線性滲流的等壓面與流線是否正交，可通過測試具有非線性滲流特征的等厚均質各向同性水平巖板內二維曲流場的等壓面與板緣壁面是否正交來判定。若不正交，誰能極之？不管是否正交，為理論非線性滲流力學奠基僅需一個曲流壓強場顯函數。

［1］齊成偉.低速滲流“非線性”探測構想［J］.天然氣技術與經濟，2015，9（6）：37-38.

［2］齊成偉.平面穩態流速場運動學通式［J］.天然氣技術與經濟，2013，7（6）：27-28.

［3］齊成偉.環形裂縫群激發的滲流場之運動學分析［J］.特種油氣藏，2014，21（4）：101-104.

［4］齊成偉.致密油藏水力碎裂區是“死油區”［J］.內蒙古石油化工，2015，41（17）：146-147.

（編輯：李臻）

A

2095-1132（2016）06-0016-06

10.3969/j.issn.2095-1132.2016.06.005

2016-10-16

2016-12-16

齊成偉（1983-），碩士，實驗師，從事流體力學、油氣水滲流力學基礎理論研究。E-mail：1261621@qq.com。