配箍率對不同剪跨比RPC梁受剪性能的影響分析

金凌志， 周家亮， 蔣春松， 梅臣， 陳璇

(桂林理工大學 廣西巖土力學與工程重點實驗室， 廣西 桂林 541004)

配箍率對不同剪跨比RPC梁受剪性能的影響分析

金凌志， 周家亮， 蔣春松， 梅臣， 陳璇

(桂林理工大學 廣西巖土力學與工程重點實驗室， 廣西 桂林 541004)

為了探究不同剪跨比下配箍率對高強鋼筋活性粉末混凝土(RPC)簡支梁受剪性能的影響，對兩組剪跨比(2.25，3.0)共6根不同配箍率的HRB500級鋼筋RPC梁進行受剪性能試驗.驗證試驗梁截面應變平截面假定，分析斜裂縫形態(tài)、開裂荷載與配箍率及剪跨比的關系，并提出基于修正壓力場理論的HRB500級鋼纖維RPC梁抗剪承載力的計算程序.研究表明：兩組不同剪跨比下的試驗梁在加載初始階段均符合平截面假定，但達到40.4%極限荷載后，這種假定將不再滿足；高強鋼筋RPC梁的斜裂縫形態(tài)主要以腹剪型斜裂縫為主，其產(chǎn)生與配箍率及剪跨比相關，配箍率和剪跨比越大越不易產(chǎn)生主斜裂縫，但剪跨比的影響明顯大于配箍率；基于修正壓力場理論的計算程序比較適用于鋼纖維高強鋼筋RPC梁抗剪承載力的計算，其計算值與試驗值吻合良好. 關鍵詞： 活性粉末混凝土； 簡支梁； 剪跨比； 配箍率； 修正壓力場理論

自活性粉末混凝土(reactive powder concrete，RPC)問世以來，國內(nèi)外學者始終在探究其材料乃至構件的力學性能.VOO等[1-2]通過7根預應力RPC無腹筋梁的受剪性能試驗研究，認為預應力變化、鋼纖維種類及摻量的變化對受剪承載力的影響顯著；徐海斌等[3]通過對超高性能混凝土梁抗剪承載力計算方法的對比分析，對修正壓力場理論的相關方程進行了修正，從而得到了適合計算超高性能混凝土梁抗剪承載力的相關方程，但修正壓力場理論的計算結果相對比較保守.金凌志等[4]對4根HRB500級鋼筋RPC簡支梁進行受剪性能試驗，并基于試驗數(shù)據(jù)建立了高強鋼筋RPC簡支梁抗剪承載力計算公式.但目前專門針對不同剪跨比條件下的高強鋼筋RPC梁受剪性能的研究還比較少.因此，本文選取兩種剪跨比條件下，以配箍率為主要參數(shù)，進行6根高強鋼筋RPC簡支梁的受剪性能試驗研究，并提出基于修正壓力場理論的鋼纖維高強鋼筋RPC梁受剪承載力的計算方法.

1 試驗概況

1.1 試驗設計

共設計6根2組剪跨比HRB400級高強箍筋簡支梁，一組剪跨比λ=2.25，另一組λ=3.0，主要研究對象為配箍率.截面形狀均為矩形，b×h=150 mm×250 mm，梁長為2 200 mm，計算跨度為1 800 mm.為了保證剪跨區(qū)的剪切破壞先于跨中彎曲破壞，在梁底部配置了5根直徑為25 mm的HRB500級縱筋.試件配筋圖，如圖1所示，試件L5配筋與試件L2相同.試件主要參數(shù)，如表1所示.其中：λ為剪跨比；h0為有效高度；ρf為鋼纖維體積摻量；ρsv為配箍率；ρs為縱筋率.

(a) 試件L1 (b) 試件L2，L5 (c) 試件L3 (d) 試件L4 (e) 試件L6 (ρsv=0%) (ρsv=0.252%) (ρsv=0.503%) (ρsv=0.126%) (ρsv=0.377%)圖1 試件配筋圖(單位：mm)Fig.1 Reinforcement detail of specimen (unit:mm)

試驗分組試件編號h0/mmλρf/%箍筋ρsv/%縱筋ρs/%L12002．252無腹筋05258．18第1組L22002．2526@1500．2525258．18L32002．2526@750．5035258．18L42003．0026@3000．1265258．18第2組L52003．0026@1500．2525258．18L62003．0026@1000．3775258．18

1.2 試驗材料

1.2.1 原材料 RPC主要原材料：42.5硅酸鹽水泥；石英砂，粒徑范圍為0.36～0.60 mm；石英粉,平均粒徑為40 μm；微硅粉，比表面積為2.0×104m2·kg-1，平均粒徑范圍為0.1～0.2 μm；硅微粉，粒徑在2 μm以下，平均粒徑為0.31 μm；鍍銅光面平直鋼纖維，長徑比為64，抗拉強度大于1.2 GPa；C900聚羧酸高效減水劑，減水率為25%.

1.2.2 試驗配比 經(jīng)篩選多組配比，選擇的RPC配合比,如表2所示.表2中:鋼纖維為體積分數(shù)，其他均為質(zhì)量分數(shù).

表2 活性粉末混凝土配合比Tab.2 Mixture ratio of reactive powder concrete %

1.3 材料力學性能

1.3.1 混凝土力學性能 參照GB/T 50081-2002《普通混凝土力學性能試驗方法標準》，測得RPC試塊的立方體(100 mm)和棱柱體(100 mm×100 mm×300 mm)的抗壓強度fcu和fc分別為150.8，144.5 MPa,彈性模量Ec為4.55 MPa，棱柱體(100 mm×100 mm×400 mm)的劈裂強度fcra為7.96 MPa.

1.3.2 鋼筋力學性能 參照GB/T 228-2002《金屬材料室溫拉伸試驗方法》進行測試，HRB500級受力縱筋和HRB400級箍筋的力學性能,如表3所示.表3中：d為直徑；fy,fu分別為屈服強度和極限強

表3 鋼筋拉伸試驗結果Tab.3 Tensile test results of steel bar

度;Ec為彈性模量.

1.4 測點布置

測點布置圖,如圖2所示.測點采用四分點單調(diào)靜態(tài)加載，試驗梁的加載在裂縫寬度小于0.3 mm前，按10%極限荷載分級加載；裂縫即將出現(xiàn)時，按5%加載；裂縫出現(xiàn)后，再按10%加載；裂縫寬度臨近承載力極限狀態(tài)下所允許的1.5 mm時，再按5%加載，直至破壞.每級荷載的加載間歇時間15 min，使各儀表讀數(shù)趨于穩(wěn)定，以便讀取記錄數(shù)據(jù).在箍筋、縱筋及RPC的剪跨段均粘貼電阻應變片,通過靜態(tài)應變測試系統(tǒng)采集應變數(shù)據(jù)，支座及跨中均布置位移計量測試驗梁的撓度.

圖2 測點布置圖Fig.2 Test point arrangement

2 試驗結果及分析

2.1 平截面假定分析

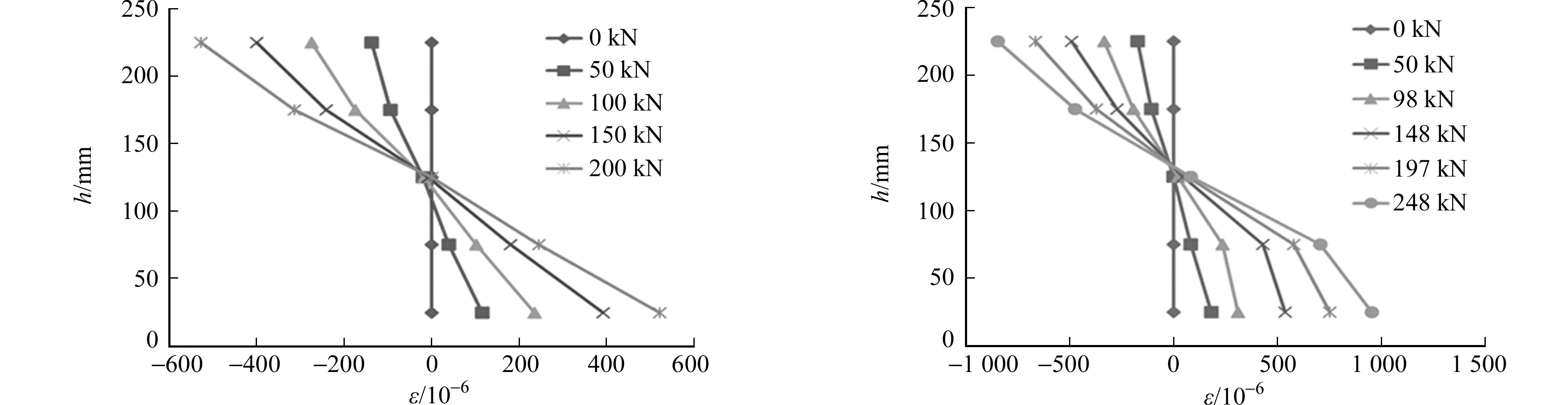
(a) L1(λ=2.25，ρsv=0%) (b) L5(λ=3.0，ρsv=0.252%)圖3 部分試驗梁的跨中截面應變Fig.3 Mid-span section strain of some specimens

部分試驗梁的跨中正截面混凝土應變分布情況，如圖3所示.圖3中：h為距梁底的距離；ε為應變.由圖3可知：在加載初始階段均符合平截面假定，但RPC開裂后，由于位于構件底端的應變迅速增大，應變很快超出量程而無法測得.普通鋼筋混凝土梁沒摻入鋼纖維，開裂后混凝土裂縫處的應力為0[5]，梁發(fā)生內(nèi)力重分布，平截面假定失效[6].RPC試驗梁達到一定荷載后產(chǎn)生彎剪裂縫，位于底端的混凝土首先開裂，開裂處鋼纖維應力突增，鋼纖維逐漸被拔出，微裂縫繼續(xù)向上發(fā)展，鋼纖維一旦屈服該處混凝土的應力也趨于0，其平截面假定不再成立.但這種現(xiàn)象明顯晚于普通鋼筋混凝土梁.

由圖3還可知：試塊截面的混凝土上下應變相差不大，說明在荷載較小時，所有試驗梁均基本符合平截面假定，但是加載到極限荷載的20.5%～40.4%時，混凝土應變不再保持平面，平截面假定失效.由于試驗構件數(shù)量有限，這種平截面假定失效的加載值有待進一步界定.

2.2 斜裂縫形成及發(fā)展

試驗梁的破壞形態(tài)，如圖4所示.由圖4可知:所有試驗梁均產(chǎn)生斜裂縫，其中,L1～L4的主斜裂縫比較明顯.試驗梁之所以產(chǎn)生具有一定間距的斜裂縫，主要是由于梁中箍筋與縱筋的作用[5].

(a) L1(λ=2.25，ρsv=0%)裂縫形態(tài) (b) L2(λ=2.25，ρsv=0.252%)裂縫形態(tài)

(c) L3(λ=2.25，ρsv=0.503%)裂縫形態(tài) (d) L4(λ=3，ρsv=0.126%)裂縫形態(tài)

(e) L5(λ=3，ρsv=0.252%)裂縫形態(tài) (f) L6(λ=3，ρsv=0.377%)裂縫形態(tài)圖4 試驗梁破壞形態(tài)Fig.4 Failure form of beams

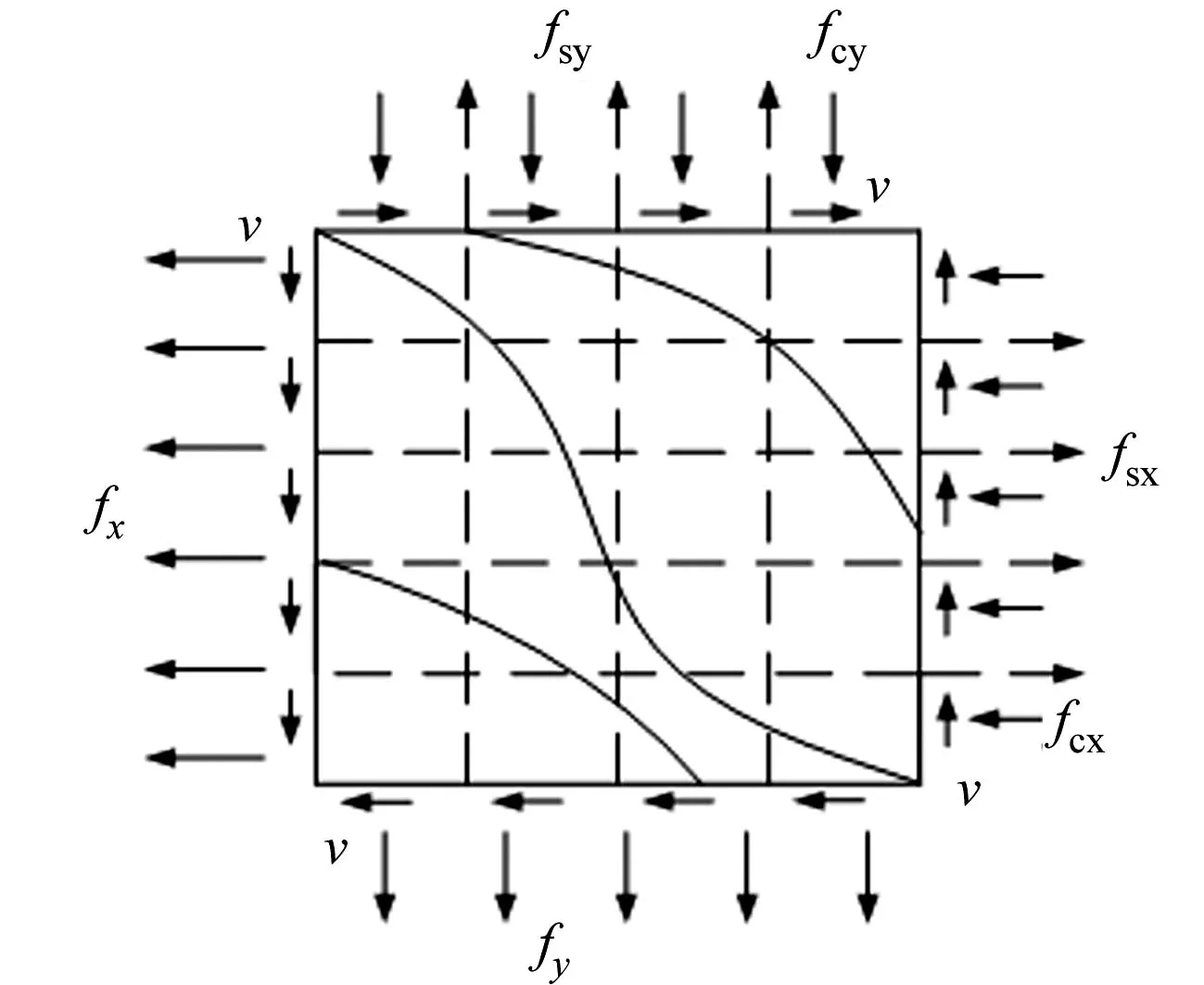
圖5 試驗梁受力分析Fig.5 Force analysis of beams

鋼筋混凝土受力單元體的受力分析，如圖5所示.由圖5可知：垂直于鋼筋方向的混凝土受到正應力和剪應力，從而使單元體受力達到平衡，當混凝土應力超過其開裂荷載對應的開裂應力后即出現(xiàn)裂縫.斜向裂縫的發(fā)展具有一定的間距，可從鋼筋縱、橫方向應力角度分析，若試件只受縱向水平應力，則產(chǎn)生的平行箍筋分部豎向裂縫，若試件只受橫向應力，則產(chǎn)生平行于縱筋的水平裂縫，兩種鋼筋應力及混凝土應力的疊加最后形成圖5所示的斜裂縫.6根試驗梁受力后,均首先在剪跨區(qū)中部出現(xiàn)腹剪裂縫，而后裂縫向兩端發(fā)展.

高強鋼筋RPC梁的斜裂縫形態(tài)以腹剪型斜裂縫為主，主要是由于RPC具有較高的抗壓強度，縱筋率較大，試驗梁底部的縱筋產(chǎn)生了較強的銷栓作用，明顯增大了梁的底部剛度，故裂縫率先從剛度較為薄弱的梁腹部產(chǎn)生.臨界主斜裂縫的形成與剪跨比和配箍率均相關，剪跨比為2.25的L1～L3，配箍率分別為0%,0.252%,0.503%，均產(chǎn)生主斜裂縫.剪跨比為3.0的試驗梁，只有配箍率為0.126%的L4產(chǎn)生主斜裂縫，而配箍率較高的L5,L6(ρsv為0.252%,0.377%)并沒有形成主斜裂縫.上述兩組試驗梁表明，剪跨比和配箍率越大都越不容易產(chǎn)生主斜裂縫，但是相對配箍率而言,剪跨比的影響更大.

圖6 配箍率對斜截面開裂荷載的影響Fig.6 Influence of stirrup ratio on crack load in inclined section

2.3 配箍率-開裂荷載曲線

剪跨比λ為2.25和3.0的配箍率(ρsv)-開裂荷載(fcr)影響曲線，如圖6所示.由圖6可知：剪跨比為2.25的試驗梁，開裂荷載曲線近似為一條水平直線，變化幅度很小，而剪跨比為3.0的曲線變化幅度相對稍大，但二者的開裂荷載基本接近.表明配箍率對兩組剪跨比下,試驗梁的開裂荷載影響甚微.究其原因是斜裂縫出現(xiàn)前，拉應力主要由RPC承擔，箍筋受力很小，甚至可以忽略；但裂縫發(fā)展到與箍筋相切的位置時，箍筋的應力突然增大，開始承擔大部分拉應力，使得混凝土所受的應力大為減小，因而抑制了斜裂縫的發(fā)展.

3 受剪承載力計算

研究表明，將經(jīng)典的修正壓力場理論直接應用于RPC梁計算將導致受剪承載力的計算值與試驗值相差較大[7].這主要由于普通混凝土的本構模型并不適用于RPC，普通混凝土強度相對較低，且未加入鋼纖維，其本構關系過于保守，低估了RPC的抗拉和抗剪承載力.RPC具有較高的強度，且摻入的鋼纖維能有效提高梁的受剪承載力[8]，因此,需要將RPC主拉、主壓應力-應變的本構關系進行修正.

主拉應力-應變的本構關系為

(1)

主壓應力-應變的本構關系為

(2)

圖7 鋼筋應力應變曲線Fig.7 Stress-strain curve of steel bar

箍筋、縱筋的本構關系均采用彈性-全塑性曲線,如圖7所示,其表達式為

(3)

將式(1)～(3)代入編制的修正壓力場理論計算程序，運行流程[9]如下：

1) 讀取試驗梁各參數(shù)；

2) 選擇初始主拉應變ε1(一般取0.001)；

3) 選擇合適的斜裂縫傾角θ值；

5) 選擇箍筋應力fv；

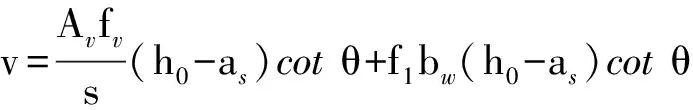
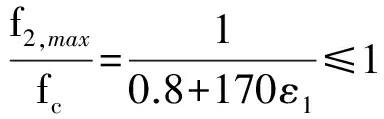
9) 判斷是否滿足f2≤f2，max，是則繼續(xù)運算，否則混凝土被壓碎，結束程序；

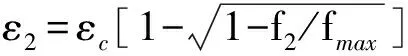
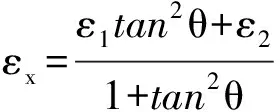
12) 判斷是否滿足fv=Esεy≤fsy，是則繼續(xù)進行構件受彎階段的計算，否則返回步驟5)重取fv；

13) 計算M=V×a；

14) 根據(jù)混凝土平截面假定選擇合適的混凝土壓應變εt(從0開始疊代計算)；

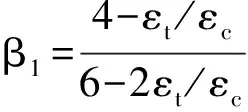
16) 由xc=hεt/(2εt+2εc)求得xc；

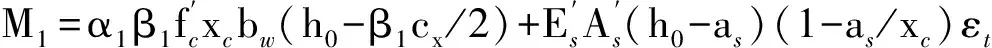
18) 判斷外力產(chǎn)生的彎矩M是否等于M1，滿足則繼續(xù)運算，不滿足則返回步驟14)重新取εt；

19) 驗證軸力N=Np-(Vcotθ-f1bwh0)是否滿足N=0，滿足則結束程序，不滿足則返回步驟3)重新選定斜裂縫傾角θ值；

20) 輸出承載力等各計算參數(shù).

以上公式中，無腹筋梁L1按有腹筋程序進行計算，箍筋間距取剪跨長450mm;sm，θ為斜裂縫間長度;sm，x，sm，y分別代表水平、豎直方向的裂縫間長度;sm,x取為箍筋間距;sm,v取上部縱筋到分布鋼筋間的距離；h0為截面有效高度，bw為試件寬度；εc為RPC極限壓應變，取0.003 18；εt為假定的混凝土壓應變；εx,εy為試件水平、豎直方向的平均應變；fsy為箍筋屈服強度，取實測值472MPa；xc為RPC截面受壓區(qū)高度；M1,M分別為內(nèi)、外力產(chǎn)生的力矩；Np為彎矩產(chǎn)生的軸力；其他參數(shù)同上.考慮到程序的收斂性，在驗證軸力N及內(nèi)外彎矩M1-M是否為0時，取相對誤差足夠小即滿足要求.

將試驗梁數(shù)據(jù)及文獻[10]數(shù)據(jù)代入編寫的Fortran程序，計算結果如表4所示.表4中：MCFT為按以上程序計算的修正壓力場理論計算值;Vcr,Vex分別為開裂荷載、抗剪承載力的試驗值.

表4 修正壓力場理論程序計算值與試驗值對比一覽Tab.4 Shear bearing capacity comparison between program calculation value of MCFT results and test results

續(xù)表 Continue table

由表4可知：試驗值與按照修正壓力場理論程序計算的理論值對比均值為1.042，均方差0.105，變異系數(shù)0.100，吻合良好.這說明基于修正壓力場理論且考慮鋼纖維作用的計算程序比較適用于高強鋼筋RPC簡支梁抗剪承載力的計算，可為工程應用提供參考.

4 結論

1) 剪跨比為2.25和3.0而配箍率不同的兩組試驗梁，在受荷初始階段均符合平截面假定，但加載到極限荷載的24.5%～40.4%時，這種假定將不再滿足.

2) 兩組不同剪跨比參數(shù)為配箍率的試驗梁研究表明，高強鋼筋RPC梁的斜裂縫形態(tài)主要以腹剪型斜裂縫為主，主斜裂縫的產(chǎn)生與配箍率和剪跨比有關，配箍率和剪跨比越大越不容易產(chǎn)生主斜裂縫，但剪跨比對主斜裂縫形成的影響程度明顯大于配箍率.

3) 對于相同剪跨比的試驗梁，配箍率對試驗梁的剪切開裂荷載影響并不明顯，開裂荷載的產(chǎn)生主要取決于RPC的抗拉強度，所以RPC的抗拉強度不容忽視.

4) 所編制的基于修正壓力場理論且考慮鋼纖維作用的計算程序可用于HRB500級RPC簡支梁受剪承載力的計算，其理論值計算值與實際值吻合良好，對實際工程的應用有一定的借鑒作用.

[1] VOO Y L，F(xiàn)OSTER S J，GIBERT R I.Shear strength of fiber reinforced reactive powder concrete prestressed girders without stirrups[J].Journal of Advanced Concrete Technology，2006，4(1):123-132.

[2] VOO Y L，POON W K，F(xiàn)OSTER S J.Shear strength of steel fiber-reinforeced ultrahigh-performance concrete beams without stirrups[J].Journal of Structural Engineering，2010，136(11):1393-1400.

[3] 徐海賓，鄧宗才.超高性能混凝土梁抗剪承載力計算方法[J].華中科技大學學報(自然科學版)，2015，43(7):24-28,71.

[4] 金凌志，張猛，李麗.高強鋼筋活性粉末混凝土梁受剪承載力公式淺析[J].鄭州大學學報(工學版)，2015,36(5):92-95.

[5] 魏巍巍.基于修正壓力場理論的鋼筋混凝土結構受剪承載力及變性研究[D].大連:大連理工大學,2011:139-159.

[6] 呂艷梅.高強箍筋高強混凝土梁抗剪性能試驗研究與理論分析[D].長沙:湖南大學,2007:81-82.

[7] 鄧宗才，周冬至，程舒.配筋活性粉末混凝土梁抗剪承載力[J].哈爾濱工程大學學報，2014，35(12):1512-1518.

[8] 鄧宗才，王海忠，劉少新，等.基于修正壓力場理論的活性粉末混凝土梁抗剪承載力計算[J].河北工業(yè)大學報，2014，43(6):22-25.

[9] 徐東坡.基于修正壓力場理論的混凝土梁抗剪研究[D].大連:大連理工大學,2006:30-34.

[10] 金凌志，梅臣.配箍率對高強鋼筋RPC梁抗剪性能影響研究[J].鐵道科學與工程學報，2016，13(4)：711-716.

(責任編輯： 黃曉楠 英文審校： 方德平)

Influence of Stirrup Ratio on Shear Behavior of RPC Beams Under Different Shear Span Ratio

JIN Lingzhi， ZHOU Jialiang， JIANG Chunsong，MEI Chen， CHEN Xuan

(Key Laboratory of Guangxi Geotechnical and Geotechnics Engineering，Guilin University of Science and Technology, Guilin 541004， China)

In order to discuss the influence of stirrup ratio on shear behavior of reactive powder concrete (RPC) simply supported beams with high-strength stirrups under different shear span ratio, six RPC beams with different stirrup ratio under two different shear span ratio (2.25 and 3.0) were experimented to verify the plane-section assumption of strain， to analyze the relationship among the shape of the inclined crack， the crack load， the shear span ratio and the stirrup ratio， then the calculation program of shear capacity of the steel fiber RPC beams with HRB500 stirrups were proposed based on the modified compression field theory (MCFT). It is showed that the two groups of test beams with different shear span ratio are in agreement with the plane-section assumption at the initial stage of loading， but this assumption is not valid when the load is over 40.4% of the ultimate value. The oblique cracks of RPC beams with high-strength stirrups are mainly the web-shear crack， which is related to the stirrup ratio and shear span ratio. As the shear span ratio and stirrup ratio increase, the main diagonal cracks occur seldom， the influence of shear span ratio is greater than stirrup ratio. This calculation program is suitable for the shear capacity of steel fiber reinforced high strength RPC beams based on the modified compression field theory， the calculated values agree well with the test results. Keywords： reactive powder concrete； simply supported beams； shear span ratio； stirrup ratio； modified compression field theory

10.11830/ISSN.1000-5013.201701007

2016-07-17

金凌志(1959-)，女，教授，主要從事新型材料混凝土結構的研究.E-mail:jlz-5904@163.com.

國家自然科學基金資助項目(51368013)； 廣西重點實驗室科研基金資助項目(2015-A-02)

TU 375.1

A

1000-5013(2017)01-0038-07