一類三階三點邊值問題正解的存在性
程德勝, 武晨
(江蘇聯合職業技術學院南京分院 基礎課程教學部, 南京 江蘇 210019)

一類三階三點邊值問題正解的存在性
程德勝, 武晨
(江蘇聯合職業技術學院南京分院 基礎課程教學部, 南京 江蘇 210019)
考慮一類三階三點邊值問題u?(t)+a(t)f(u(t))=0,t∈(0,1),u(0)=u′(0)=0,u′(1)-αu′(η)=λ, 其中,0<η<1,0<α<1/η,λ>0,f滿足超線性或者次線性條件,利用錐上的不動點定理,得到上述邊值問題解的存在性結果.結果表明:文中方法進一步改進和推廣了吳紅萍的結果. 關鍵詞: 三階三點邊值問題; 錐; 格林函數; 不動點定理
三階微分方程邊值問題是研究奇數階邊值問題的基礎,由于其廣泛的物理背景和現實意義,三階邊值問題引起了許多學者的關注,并且取得了較多成果[1-10]. 吳紅萍[2]考慮了三階三點邊值問題u?(t)+a(t)f(u(t))=0,t∈(0,1),u(0)=u′(0)=0,u′(1)-αu′(η)=λ.其中:0<η<1;0<α<1/η;λ>0.通過應用Leggett-Wilmlias不動點定理得到上述邊值問題有3個正解的存在性.但作者僅考慮在上述條件下解的存在性,并沒有考慮到當f滿足超線性或次線性條件下,上述邊值問題的解是否存在.本文研究一類三階三點邊值問題,即
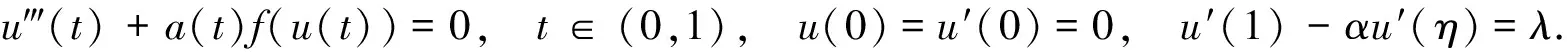
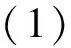
1 一些引理及定義
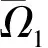
引理2[3]邊值問題 u?(t)+a(t)f(u(t))=0,t∈(0,1),u(0)=u′(0)=0,u′(1)-αu′(η)=λ,有唯一解,即
(2)
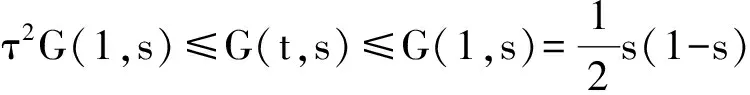
引理4[3]對任意(t,s)∈[0,1]×[0,1],有0≤G1(t,s)≤s(1-s).
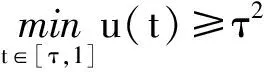
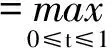
(3)
由引理3可得
則有
(4)
當t∈[τ,1]時,由引理3和式(4),有
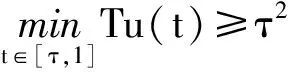
2 主要結果
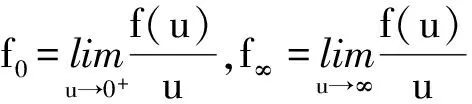
定理1 假設f0=0,且f∞=∞(超線性),則邊值問題(1)至少存在一個正解.
證明 因為f0=0,所以存在R1>0,使0≤u≤R1時,有f(u)≤εu,t2≤ε‖u‖成立.其中,ε為大于0的常數,且滿足
(5)
當u∈K,‖u‖=R1時,由引理3和式(5),有
(6)
令Ω1={u∈E:‖u‖ 另一方面,由f∞=∞可知,存在R2>R1,使u≥τ2R2時,有f(u)≥ρu成立.其中,ρ>0,且滿足 (7) 令Ω2={u∈E:‖u‖ 定理2 假設f0=∞,且f∞=0(次線性),則邊值問題(1)至少存在一個正解. 證明 因為f0=∞,則存在R3>0,使0≤u≤R3時,有f(u)≥δu成立.其中,δ>0,且滿足 (8) 當u∈K,‖u‖=R3時,由式(8)可得 令Ω3={u∈E:‖u‖ (9) 下面分兩種情況進行討論. 1) 如果f是有界的,即存在M>0,當u∈[0,+∞]時,有f(u)≤M成立,此時,令 從而‖Tu‖≤‖u‖. 因此,‖Tu‖≤‖u‖.無論哪一種情況,都可以令Ω4={u∈E:‖u‖ 建立適當的格林函數,選擇合適的錐,運用錐拉伸與壓縮不動點定理,對一個含參數的三階邊值問題在滿足超線性或者次線性條件下正解的存在性進行了探究,得到了一些新的推廣的結果,也豐富了對錐拉伸壓縮不動點定理的理論分析. [1] 楊春風.一類三階三點邊值問題正解的存在性和不存在性[J],山東大學學報(理學版),2012,47(10):109-115. [2] 吳紅萍.一類三階三點非齊次邊值問題的兩個正解[J].西北師范大學學報(自然科學版),2012,48(6):9-12. [3]SUNYongping.Positivesolutionsforthird-orderthree-pointnonhomogeneousboundaryvalueproblems[J].ApplMathLetters,2009,22(1):45-51. [4] 王全義,鄒黃輝.一類n階非線性三點邊值問題單調正解的存在性[J].華僑大學學報(自然科學版),2014,35(3):344-348. [5] 王全義,鄒黃輝.非線性奇異三階兩點邊值問題單調正解的存在性[J].華僑大學學報(自然科學版),2012,33(6):699-704. [6] 高婷,韓曉玲.三階無窮多點邊值問題正解的存在性[J].四川大學學報(自然科學版),2016,53(1):35-41. [7] 武晨.帶有積分型邊值條件的奇異的n階邊值問題無窮多正解的存在性[J].淮北師范大學學報(自然科學版),2015(3):14-17. [8] 孫建平,張小麗.非線性三階三點邊值問題正解的存在性[J].西北師范大學學報(自然科學版),2012,48(3):1-4. [9] 孫建平,彭俊國,郭麗君.非線性三階三點邊值問題的正解[J].蘭州理工大學學報,2009,35(1):139-142. [10] 呂學哲,裴明鶴.一類三階三點邊值問題正解的存在性[J].北華大學學報(自然科學版),2014(5):577-580. (責任編輯: 錢筠 英文審校: 黃心中) Existence of Positive Solution for Third-Order Three-Point Boundary Value Problems CHENG Desheng, WU Chen (Basic Courses Teaching Department, Branch of Nanjing Jiangsu Union Technical Institute, Nanjing 210019, China) We study the existence of positive solution to the following third-order three-point boundary value problemsu?(t)+a(t)f(u(t))=0,t∈(0,1),u(0)=u′(0)=0,u′(1)-αu′(η)=λ, where 0<η<1, 0<α<1/η,λ>0. By using fixed point theorem in cones, we obtain the existence of the positive solution iffis either superlinear or sublinear. Our results extend and improve some results made by Wu Hongping. Keywords: third-order three-point boundary value problem; cone; Green fuction; fixed point theorem 10.11830/ISSN.1000-5013.201701025 2016-11-25 程德勝(1970-),男,副教授,主要從事非線性泛函分析、課程論的研究.E-mail:cdsyycxr@sina.com. 國家自然科學基金資助項目(60773128) O 175.8 A 1000-5013(2017)01-0127-04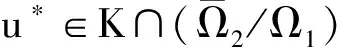
3 結束語

