基于氣泡群相間作用力模型的加壓鼓泡塔流體力學模擬

劉鑫，張煜，張麗，靳海波

（1北京石油化工學院化學工程學院，北京 102617；2中科合成油技術有限公司研發中心，北京 101407）

基于氣泡群相間作用力模型的加壓鼓泡塔流體力學模擬

劉鑫1,2，張煜2，張麗2，靳海波1

（1北京石油化工學院化學工程學院，北京 102617；2中科合成油技術有限公司研發中心，北京 101407）

目前，多數文獻報道了冷態加壓湍動鼓泡塔內流動特征，并且通過實驗數據回歸相關經驗關聯式。然而，此類關聯式適用范圍有限，難以直接外推到工業鼓泡塔反應器條件。因此，在FLUENT平臺上建立了基于氣泡群相間作用力的、動態二維加壓鼓泡塔計算流體力學模型。通過數值模擬考察了操作壓力為0.5～2.0 MPa，表觀氣速為0.20～0.31 m·s?1，內徑0.3 m鼓泡塔內流場特性參數分布，并且與冷態實驗數據進行比較。結果表明，采用修正后的氣泡群曳力模型、徑向力平衡模型以及壁面潤滑力模型描述氣泡群相間作用力，能夠較為準確地反映平均氣含率和氣含率徑向分布隨操作壓力和表觀氣速變化的規律。

鼓泡塔；氣液兩相流；計算流體力學；氣泡群曳力模型；徑向力平衡模型；壁面潤滑力模型

引 言

煤間接液化技術作為煤炭清潔高效利用的重要手段之一，它是以煤炭為原料制取目標產品為液態燃料的技術。隨著以費托合成工藝為核心的煤炭間接液化技術的重要性日益突顯，作為費托合成反應的載體，費托合成反應器得到了快速發展。費托合成反應器先后經歷了固定床、流化床和漿態床 3個不同階段，其中采用漿態床反應器生產的柴油，具有高能量密度、低排放、品質好等優點，因此，漿態床已成為煤制油進行費托合成反應的主流反應器[1]。

工業鼓泡塔反應器通常帶壓操作，并且表觀氣速較高，處于湍流鼓泡狀態。目前對于加壓鼓泡塔的研究大多集中于冷態實驗測量和流動規律的總結，根據實驗數據回歸經驗關聯式，缺乏能夠詳細描述加壓鼓泡塔的流體力學模型。Krishna等[2]根據加壓氣泡界面的Kelvin-Helmholtz不穩定性分析和氣泡曳力模型，將壓力影響作為氣相密度修正項ρG/ρG,1atm引入曳力系數計算公式。建立了雙氣泡二維軸對稱CFD模型，用CFX軟件模擬了塔徑0.15 m加壓湍動鼓泡塔充分發展段的液相軸向擴散系數及氣含率，并與冷態實驗數據進行比較。在高氣速下，該模型計算的氣含率明顯高于實驗測量值。Chen等[3]建立了結合氣泡群體平衡方程（PBM）的 3D雙流體和混合物模型，用 FLUENT模擬了塔徑為0.162 m加壓鼓泡塔流場。考慮到Krishna等[2]的模型在高氣速下對氣含率高估，認為造成偏差的原因可能是，高氣速下兩相湍流和尾渦的卷吸作用影響顯著。為了改進模型的計算準確度，Chen等[3]引入(ρG/ρG,1atm)0.25修正氣泡曳力項。該模型采用耦合PBM的3D模擬，為保證計算準確度，離散網格數量隨鼓泡塔尺寸提高而快速增加，需要大量計算資源。以現有計算機運算能力，仍然難以采用此模型進行大型加壓鼓泡塔反應器 3D模擬和放大設計。

Joshi[4]認為氣泡所受的橫向作用力決定其沿塔徑向的運動模式，是湍動鼓泡塔形成氣含率不均勻分布的重要影響因素；Tabid等[5]通過3D動態模擬鼓泡塔流場，比較了不同相間作用力的影響，認為曳力、升力和湍流擴散力對氣含率和軸向液速分布影響顯著。文獻[6-8]通過引入氣泡徑向力平衡機制，確定氣含率徑向分布，一維及二維數值模擬結果與實驗數據符合較好。綜上所述，二維軸對稱模型耦合適當的相間作用力模型，能夠在可接受的計算代價下，得到較為準確的常壓鼓泡塔流場模擬結果。本文擬建立動態二維軸對稱加壓湍動鼓泡塔模型，包括徑向力平衡機制、氣泡群曳力模型和壁面潤滑力，根據內徑0.3 m加壓冷態鼓泡塔冷態實驗數據，擬合氣泡群曳力系數參數，使模型具備預測加壓湍動鼓泡塔反應器內多相流場特性，為工業漿態床反應器放大和內構件優化提供指導。

1 數學模型

1.1 守恒方程

本文所提出的雙流體加壓鼓泡塔模型，采用雷諾時均的控制方程[9-11]。與操作壓力相比，加壓鼓泡塔靜液壓相對較小，可近似認為氣體密度基本不隨軸向高度變化，冷態條件下可忽略兩相間的傳熱和傳質作用，將相間作用力以體積源項的方式，添加至動量守恒方程組中，控制方程可表示如下：

連續性方程為

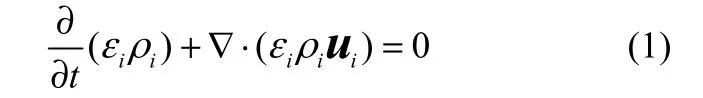
文獻[9, 11]給出了氣液兩相表達形式一致的動量守恒方程

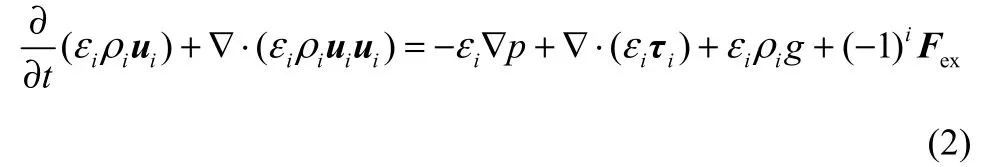
文獻[12-17]報道采用標準k-ε模型能夠描述鼓泡塔內液相湍流場，本文也采用該模型計算液相湍流動能k和湍流動能耗散率ε的分布，以及湍流黏度μt，模型方程為

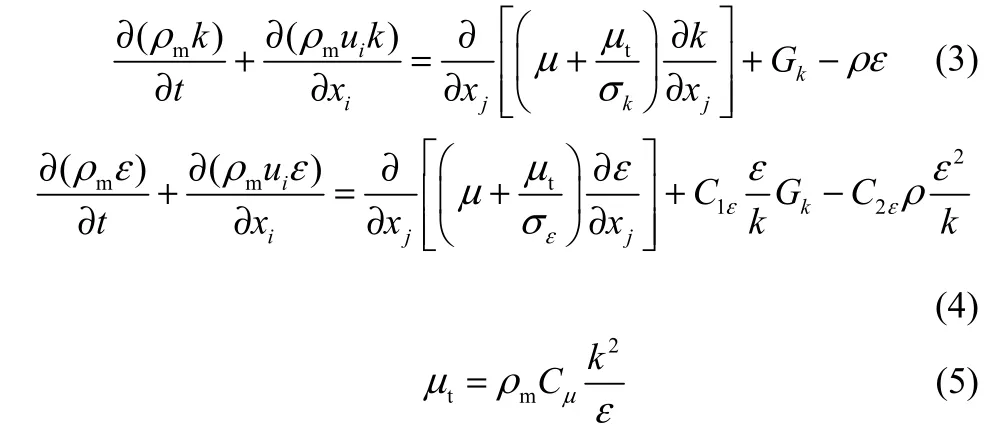
式中，參數Cμ=0.09，C1ε=1.44，C2ε=1.92，σk=1.0，σε=1.3。

1.2 相間作用力模型

鼓泡塔雙流體模型中，主要通過體積平均的相間作用力源項描述氣液相間動量傳遞[4-5,10-11]。本文所提出的加壓鼓泡塔流體力學模型，主要考慮氣泡曳力、升力、湍流擴散力和壁面潤滑力。另外，虛擬質量力表現為顆粒在加速運動時，使周圍流體也加速運動所需要額外的力，Khopkar等[18]認為虛擬質量力在氣體分布器附近更重要，而在流動主體區域的作用遠小于曳力，且本文通過實際工況模擬發現，添加虛擬質量力模型對模擬結果幾乎無影響，因此本文忽略了虛擬質量力。

1.2.1 曳力 鼓泡塔內氣泡曳力是相間作用力研究的重點之一，也是現有各種流體力學模型主要考慮的相間作用之一，甚至是許多模型中唯一考慮的相間作用力。對于鼓泡塔雙流體模型，動量守恒方程中的曳力源項通常表述為單位體積內氣泡群所產生的合曳力，表示為

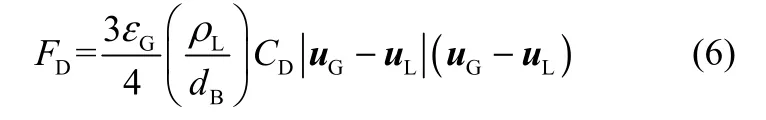
在加壓湍動鼓泡流狀態下，氣含率相對較高，氣泡在浮升過程中會受到附近氣泡的影響，需要引入氣泡群曳力系數進行修正，文獻中通常將氣泡群曳力系數CD與單個氣泡曳力系數CD0與氣含率相關聯進行修正。

文獻中給出的單氣泡曳力系數模型通常與氣泡Reynolds數Re相關。Schiller & Naumann模型常用于氣液兩相流模擬，在鼓泡塔流場數值模擬過程中穩定性較好，模型方程如下

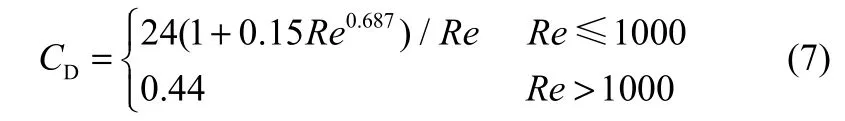
與 Schiller & Naumann模型相比，Morsi & Alexander模型更為完整，其曳力系數對氣泡Reynolds數的劃分更詳細，曳力系數與Reynolds數的關系可表示為

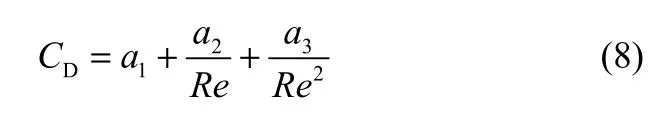
式中，a1、a2、a3為模型參數，隨Reynolds數取值區間的改變而對應不同的數值。但是，該模型的計算穩定性不及其他模型。

Lau等[19]和 Roghair等[20]采用直接數值模擬（front-tracking model，前緣追蹤模型）單個氣泡及氣泡群浮升過程，通過模擬結果擬合得到氣泡群曳力系數與氣含率和Eo數的關聯式

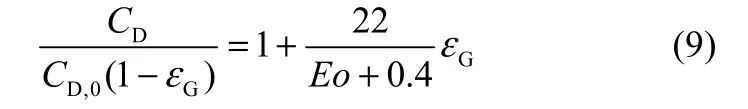
但是，Roghair等[20]未考慮操作壓力對氣泡群曳力系數的影響，因此，本文在式（9）的基礎上，根據冷態實驗[21]測量的全塔平均氣含率（壓差法測量）和氣泡直徑（電導探針測量），調整單氣泡曳力模型中的曳力系數，使平均氣含率的模擬結果符合實驗測量值。根據調定后的曳力系數、氣含率、氣泡直徑及新添加的量綱1壓力項，擬合模型參數，得到適用于加壓條件下改進的氣泡群曳力系數計算公式

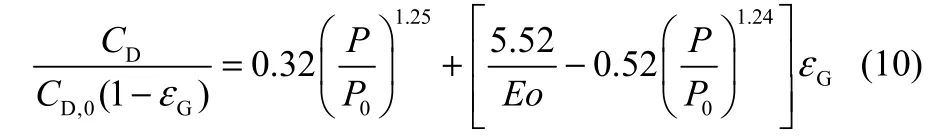
其中，CD,0表示單個氣泡的曳力系數，本文采用Schiller & Naumann模型計算CD,0，湍動鼓泡塔中氣泡的相對Reynolds數Re通常均大于1000，CD,0可取常數0.44。

1.2.2 升力 鼓泡塔內氣泡浮升運動過程中，由于液相在其運動方向的兩側流動不對稱，會造成氣泡兩側壓力不平衡，從而產生垂直于氣泡運動方向的升力。大氣泡在鼓泡塔內受到液相剪切流動、曳力以及渦旋的作用后，易發生變形，并且在氣泡的后方產生偏斜尾渦，推動氣泡橫向運動。Drew等[22]給出了單位體積內，氣泡群所受合升力的計算公式

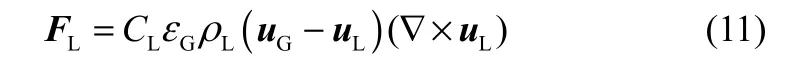
在鼓泡塔充分發展段，如果氣泡升力系數 CL所取的符號不同，氣泡升力會指向塔中心或者塔壁，使氣含率徑向分布對應形成中心高的拋物線分布，或者形成壁面峰的鞍形分布，此外，升力系數 CL取值大小會顯著影響氣含率徑向分布的梯度。

1.2.3 湍流擴散力 對于湍動鼓泡塔流場，湍流擴散力體現了氣液兩相隨機運動所產生的擴散作用，在該力的作用下氣含率徑向分布趨于均勻。Lopez de Bertodano[23]將氣泡的隨機運動類比于分子熱運動，推導出單位體積氣泡受到液相渦旋所受的擴散力表達式

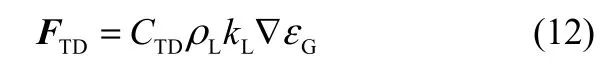
考慮到湍流擴散力主要在氣含率較高的區域起作用，因此，引入極限函數 fTD,limiting對湍流擴散力作用區域進行調整，湍流擴散力可表示為

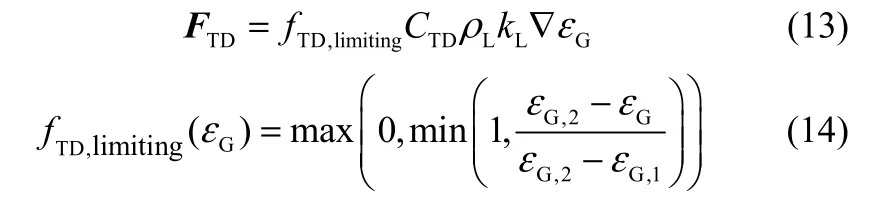
其中，εG,1和εG,2為湍流擴散力起作用的局部氣含率下限及上限值，本文所述模型中將其分別取值為0.3和0.7。

文獻[7-8]中認為鼓泡塔內徑向力作用力對氣含率的分布起著主導作用，當升力和湍流擴散力達到動態平衡，氣含率的分布也隨之趨于穩定。張煜等[7]通過常壓鼓泡塔冷態實驗數據和一維模型計算結果，確定了氣泡升力系數 CL和湍流擴散力系數CTD符合如下函數關系

式（15）中的系數0.2是一個固定的值，不隨實驗條件而改變。本模型假設該徑向力平衡機制同樣適用于加壓湍動鼓泡塔流場模擬，湍流擴散力系數 CTD取 1.0，液含率與升力系數對應情況如表 1所示。

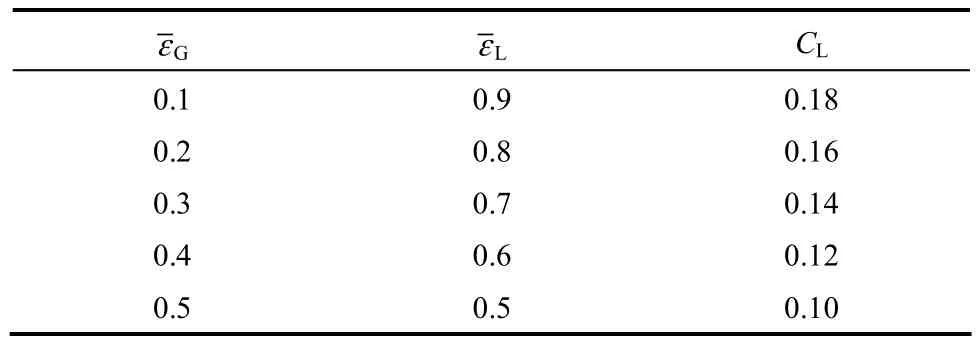
表1 不同液含率下的升力系數Table 1 Lateral lift coefficient under different liquid holdup

1.2.4 壁面潤滑力 當浮升氣泡接近壁面時，氣泡表面液體速度分布受到壁效應的影響，表現為氣泡與壁面之間的液相排出速率下降，而在另一側的排液速率增加，從而產生將氣泡推離壁面的力，稱之為壁面潤滑力[24]。本文模型采用 Tomiyama[25]的壁面潤滑力模型，單位體積的氣泡所受的壁面潤滑力可表述為

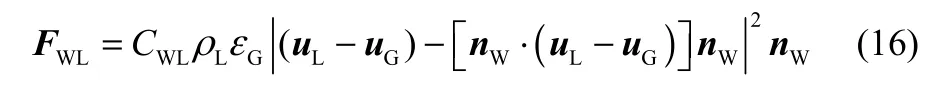
式中，壁面潤滑力系數CWL可表示為

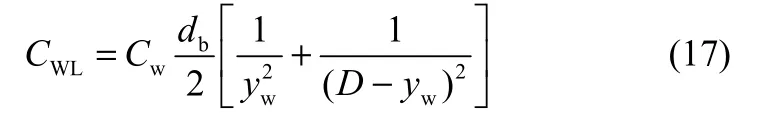
式中，yw為壁面距離，Cw可表示為氣泡Eo數的分段函數

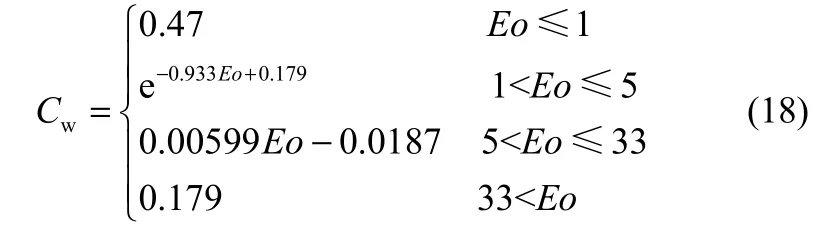
在進行加壓鼓泡塔軸對稱二維動態模擬時發現，當網格密度較高時，在充分發展段經常出現壁面氣含率高中心低的情況，這與實驗測量結果不符。當模型中考慮壁面潤滑力后，能夠有效避免出現氣含率分布的非物理解。

2 模型設置及求解方法

本文參照文獻[21]所述內徑0.3 m冷模加壓鼓泡塔裝置生成二維計算網格，計算區域寬度為0.15 m、高度為6.6 m。根據表觀氣速和操作壓力設置初始靜液位高度H0，防止膨脹床層高度超過計算域高度，造成液體溢出，靜液位設定高度為2.5～3.0 m。設定H0以下的液含率為1.0，H0以上的液含率為 0，氣液相均處于靜止狀態。邊界條件為：鼓泡塔底部的孔板分布器（r/R＜0.8）簡化為氣相速度進口邊界條件；塔頂氣相出口設置為壓力出口；中心軸采用軸對稱邊界條件；壁面的氣液相均設定為無滑移條件，湍流方程設定為標準壁面函數，如圖 1所示。本文采用文獻[21]的實驗數據作為檢驗模型的依據，其中局部氣含率、氣泡上升速度及氣泡Suater直徑，是采用雙電導探針，根據氣液兩相電導率差異較大的原理來測量的，對氣泡上升速度的測量是通過考察電導針處，一段時間時間內統計所有氣泡上升速度的數量平均獲得的。

通過用戶自定義方程UDF，將前文所述的各氣泡界面力模型嵌入FLUENT計算程序，全塔設定單一氣泡直徑等于秦玉建[21]的冷態實驗測量值。模型采用 FLUENT 15.0進行動態模擬，采用Phase-Coupled SIMPLE算法求解壓力-速度耦合，離散空間梯度使用Least Squares Cell based方法，導數采用一階迎風格式，時間導數采用一階隱式格式，為防止發散，初始時間步長為0.001 s，待流場充分發展后，可以逐漸增加步長至0.004 s。模擬結果表明，當計算物理時間達到20 s后，加壓鼓泡塔充分發展段的徑向氣含率分布基本不變，可近似認為流場充分發展，以表觀氣速0.31 m·s?1，操作壓力為0.5 MPa，距氣體分布器2.4 m處氣含率徑向分布為例，如圖2所示。本文取模擬時間50 s后的流場進行時均，圖3給出了不同采樣時間對應的時均氣含率分布，可以看出當流場基本穩定后，采樣時間大于25 s后的氣含率分布基本一致。因此，文中所述模擬均提取流場發展50 s后的數據，再時均50 s作為數值模擬結果。

圖4給出了網格數量對充分發展段氣含率徑向分布模擬結果的影響，考察了網格數量為3960、5940、17160和47520個4種不同的網格，并且均在近壁區域加密了4層邊界層網格。從圖中可以看出，加密網格對中心氣含率分布影響較小，主要使近壁面氣含率分布變得更為平滑。綜合考慮計算代價和數值模擬精度，采用網格數為5940個。

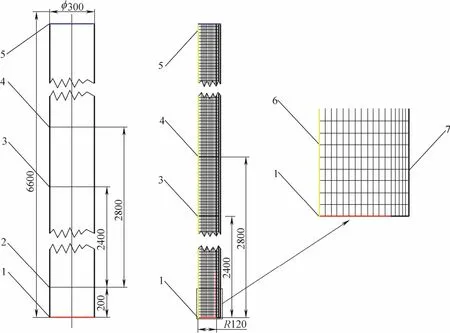
圖1 加壓鼓泡塔結構及邊界條件Fig.1 Schematic diagram of pressurized bubble column and boundary conditions

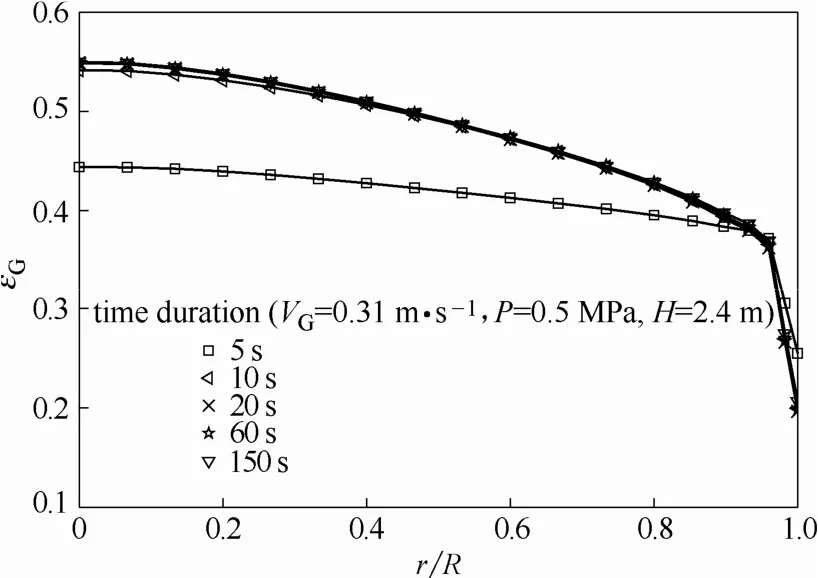
圖2 模擬的氣含率徑向分布隨時間的變化Fig. 2 Simulated radial gas holdup profiles varied with time

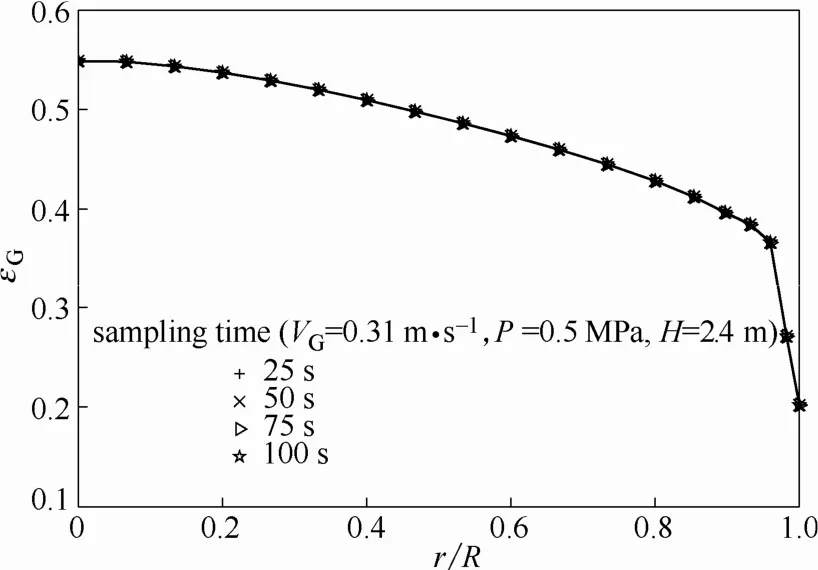
圖3 模擬時均氣含率分布隨采樣時間的變化Fig. 3 Simulated radial gas holdup profiles varied with sampling time

圖4 網格密度對氣含率徑向分布的影響Fig. 4 Influence of mesh density on radial gas holdup distribution (VG=0.27 m·s?1，P=0.5 MPa，H=2.6 m)

3 結果與討論

3.1 流場分布

鼓泡塔流場的最主要特征是氣含率在徑向上的不均勻分布，即中心區域氣含率高，邊壁處氣含率較低。這種氣含率的不均勻分布形成密度差，從而驅動液相流動，形成液相塔內的大尺寸循環流動，呈現出中心區液相向上運動，近壁區液體向下回流的規律。圖5是CFD模擬得到的，表觀氣速為0.27 m·s?1，操作壓力為1.5 MPa，內徑0.3 m加壓鼓泡塔內時均氣含率二維分布。模擬結果表明，在鼓泡塔底部，回流液體在壁面附近富集，使氣泡向塔中心集中。經過約1倍塔徑發展后，氣含率徑向分布呈現出中心高、邊壁低的趨勢，并且不隨高度變化，形成充分充分發展段，直至接近塔上部液位處。在氣體分布器上方2.6 m和3.0 m處，冷態測量得到的氣含率徑向分布基本相同，可認為處于充分發展段，模擬的氣含率分布與實驗結果符合較好，這表明，本文所提出的基于氣泡群界面力的加壓鼓泡塔二維模型，能夠確定氣含率分布。

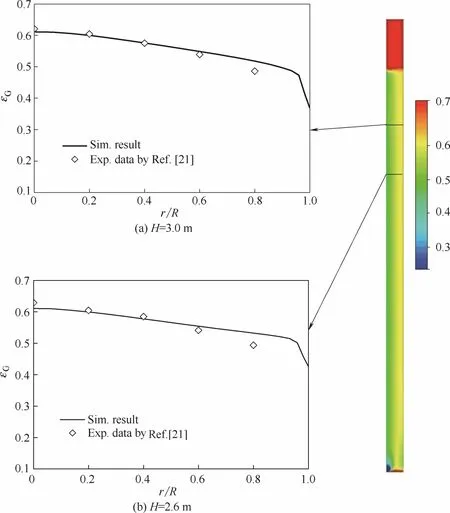
圖5 氣含率二維分布模擬結果與實驗數據的比較Fig.5 Comparison of simulated 2-D gas holdup distribution and experimental data(VG=0.27 m·s?1，P=1.5 MPa)

3.2 曳力模型比較分析

圖6（a）為操作壓力為0.5 MPa時，不同的曳力模型計算的充分發展段氣含率徑向分布與實驗結果的比較，與Schiller & Naumann模型相比，改進的氣泡群曳力模型和Morsi & Alexander曳力模型模擬結果更接近實驗值。Schiller & Naumann模型所獲得模擬結果更接近實驗值；而當操作壓力增至1.5 MPa時，Schiller & Naumann模型和Morsi & Alexander模型的氣含率分布與低壓時的模擬結果基本相同，不能反映壓力增加后局部氣含率增大的趨勢。然而，改進的氣泡群曳力模型能夠描述壓力對局部氣含率的影響，并且模擬結果與實測值符合較好，如圖6（b）所示。

圖7為不同操作壓力下，上述3種曳力模型計算的軸向氣速徑向分布與實驗數據的比較。冷態實驗數據顯示，當表觀氣速為0.27 m·s?1時，隨著操作壓力的升高，局部氣相速度略有下降。從圖7中可以看出，3種曳力模型對塔中心區域（r/R＜0.3）的氣相速度較為接近，越靠近塔壁模擬計算值與實驗值差別越大。當壓力為0.5 MPa時，改進的氣泡群曳力模型的計算結果比另兩種模型更接近實驗值。而當壓力增加到1.5 MPa時，Schiller & Naumann模型和Morsi & Alexander模型計算得到氣相速度與低壓下的計算值相比，并沒有如實驗數據表現出下降趨勢，反而略有增加，然而，改進的氣泡群壓力模型能夠定性反映軸向氣速隨操作壓力增大而減小的趨勢。由于本文給出的氣泡群壓力系數表達式是基于平均氣含率和氣泡直徑的冷態數據回歸得到的，尚且沒有考慮對氣相上升速度的修正，這可能是導致中心區域以外的軸向氣速模擬結果偏差較大的一個原因。在冷態實驗中，氣相是以氣泡離散相存在的，測量的氣相速度即是氣泡的上升速度，而模擬出來的氣相上升速度是將氣相作為連續相考慮的，即作為連續介質的氣相與液相充分混合，因此所計算出來的氣相上升速度相較于實驗測量氣泡上升速度值偏小，這可能也是氣相上升速度存在偏差的另一個原因。

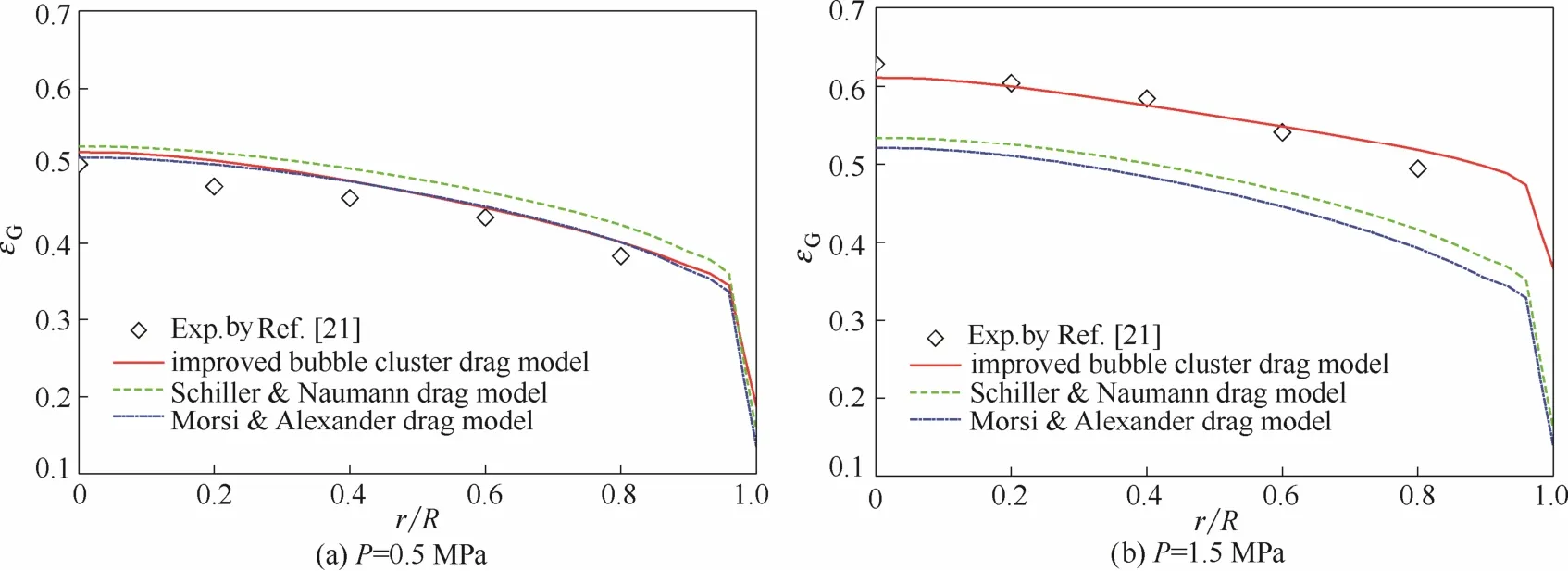
圖6 不同曳力模型對氣含率徑向分布的影響Fig.6 Effect of various drag model on radial gas holdup distribution(VG=0.27 m·s?1, H=2.6 m)

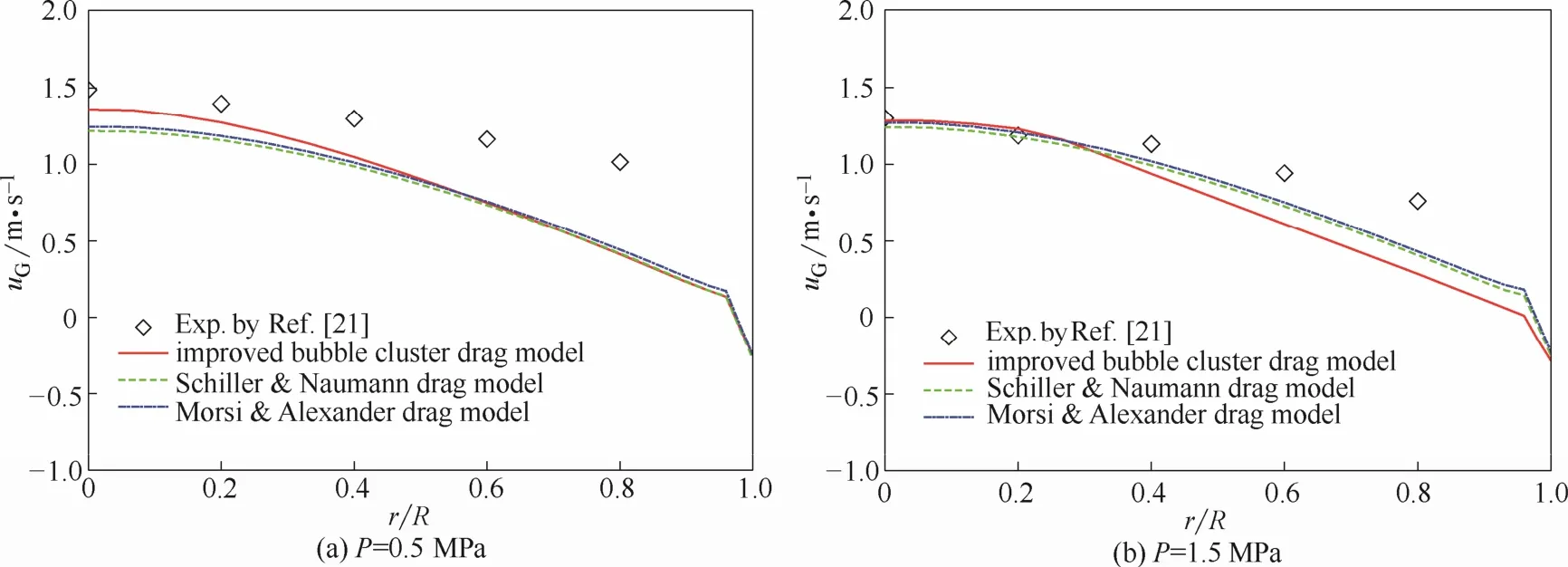
圖7 不同曳力模型對氣相上升速度徑向分布的影響Fig.7 Effect of various drag model on gas rising velocity radial distribution(VG=0.27 m·s?1,H=2.6 m)

綜上，改進的氣泡群曳力模型能夠用于不同操作壓力下的鼓泡塔流場，盡管對氣相上升速度分布模擬精度不夠理想，但是定性能夠體現壓力對軸向氣相速度的影響，并且高壓條件下模擬得到的氣含率徑向分布與實驗值符合較好。因此，該模型與Schiller & Naumann和Morsi & Alexander模型相比模擬準確度有所提高，基本能夠描述湍動加壓鼓泡塔內，操作壓力對充分發展段氣含率和軸向氣速分布的影響趨勢。

3.3 表觀氣速對流場的影響

表觀氣速是影響加壓鼓泡塔內氣液兩相流動的關鍵參數，冷態實驗結果表明，全塔平均氣含率隨表觀氣速提高而增大。表2列出了操作壓力為0.5 MPa，表觀氣速為0.20～0.31 m·s?1時，全塔平均氣含率模擬值與實驗值的比較結果，可以看出模型對平均氣含率的預報較為準確，最大誤差絕對值不超過 2%，能夠定量描述加壓鼓泡塔平均氣含率隨表觀氣速變化的規律。

圖8為上述表觀氣速下，模擬得到的局部氣含率與實驗結果的比較。冷態實驗數據顯示，隨著表觀氣速的增加，局部氣含率提高，氣含率沿徑向分布的陡峭程度基本不變。從圖8中可以看出，模擬得到的氣含率分布雖然略高于實驗測量結果，尤其是表觀氣速為0.20 m·s?1時偏差相對較大，但是模擬的氣含率分布趨勢與實驗結果較為接近。模擬和實驗結果定量上的差異，可主要歸結于兩個方面：一方面，改進的氣泡群曳力系數關聯式[式（10）]中的參數是基于壓差法測量得到的平均氣含率的數據回歸而來；另一方面，由于氣泡在浮升過程中受到液相湍流渦旋的擾動，會發生一定隨機擺動，造成氣泡與電導探針接觸點的氣泡表面法向與探針角度過大，氣泡易從探針尖端脫離，使得探針測量的局部氣含率偏小。秦玉建[21]的冷態實驗數據顯示，通過電導針測量的局部氣含率積分得到的截面平均氣含率，通常略低于差壓法的測量值，尤其當表觀氣速為0.20 m·s?1時，兩者相差較為明顯。

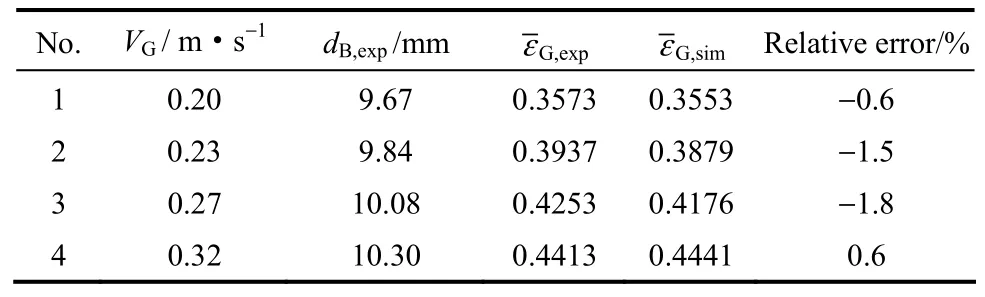
表2 不同表觀氣速下平均氣含率模擬值與實驗值比較Table 2 Comparison between simulation results and experiment values for different superficial gas velocity (P=0.5 MPa)

圖9為不同表觀氣速下，軸向氣相速度模擬與實驗結果的比較，從圖中可以看出，隨著表觀氣速由0.20 m·s?1增加到0.31 m·s?1，實驗測量的氣相速度略有提高，而徑向分布趨勢基本相同；而模擬得到的氣相速度隨著表觀氣速增加而增大，且分布變得更為陡峭，與實測結果相差較多。

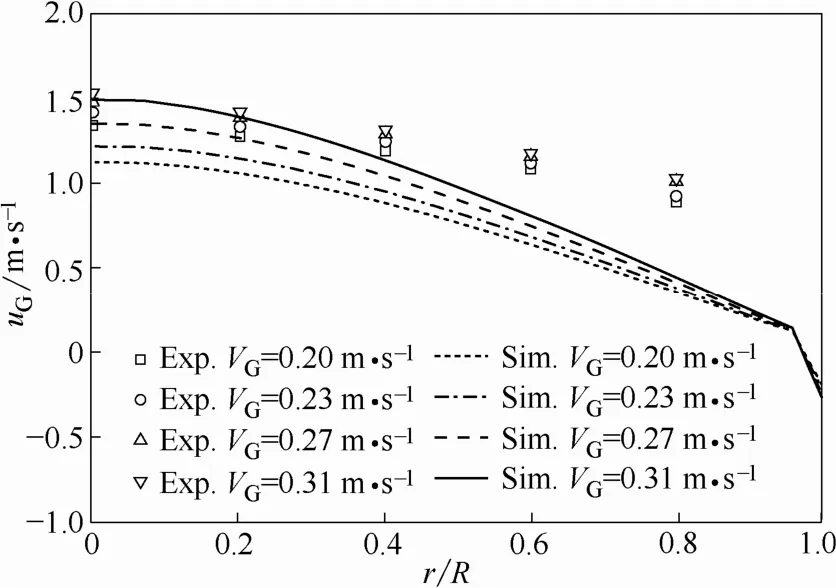
圖9 表觀氣速對軸向氣速分布的影響Fig.9 Effect of superficial gas velocity on axial gas rising velocity along radius (P=0.5 MPa, H=2.6 m)

3.4 操作壓力對流場的影響

操作壓力對流場的影響顯著，實驗表明隨著操作壓力的增加，氣泡尺寸略有減小，氣泡上升速率降低，使得氣泡在流場內停留時間增加，使氣含率明顯提高。表3給出了在表觀氣速為0.27 m·s?1，壓力為0.5 MPa～2.0 MPa下，平均氣含率模擬結果與實驗值的比較，模擬結果略低于實測值，最大相對誤差的絕對值為3.3%。

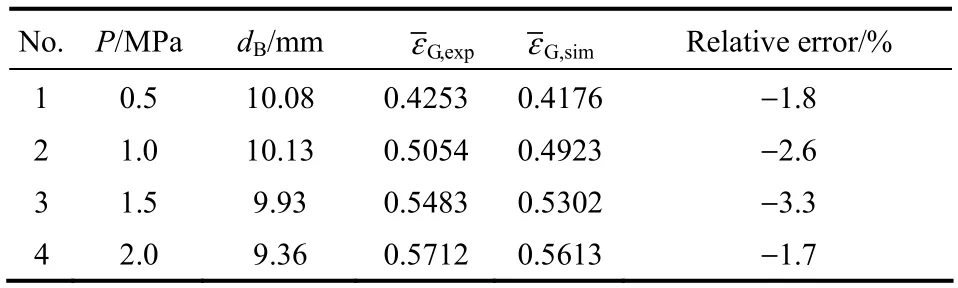
表3 不同操作壓力下平均氣含率模擬值與實驗值比較Table 3 Comparison between simulation results and experimental values under various operating pressure(VG=0.27 m·s?1)

從圖10中可以看出，壓力為0.5～1.5 MPa時，模擬的氣含率分布略高于實驗值，而當壓力達到2.0 MPa時，塔中心處實驗結果高于模擬值。數值模擬與實測的氣含率分布曲線變化趨勢基本一致，隨著操作壓力的增加兩者的氣含率均逐漸增加。但是，在部分操作壓力下，模擬的局部氣含率與實驗結果相比還存在一定偏差。

圖 11表明模擬的氣相速度隨著壓力升高而下降，與實驗結果所呈現的趨勢基本一致。然而，模擬的軸向氣相速度分布比實測分布更為陡峭，并且模擬結果在總體上也略低于實驗測量結果。由于模型假設全塔氣泡尺寸不變，而實際上湍動鼓泡塔內氣泡直徑存在一定空間分布，而氣泡運動速度通常與其尺寸相關，使得模型雖然能夠定性描述軸向氣速分布隨操作壓力變化的基本趨勢，但是在定量上還存在明顯偏差。在后續工作中將引入數量衡算方程（population balance equation），模擬得到加壓鼓泡塔內氣泡尺度分布，并以此校正氣相速度分布，提高模型的預測精度。

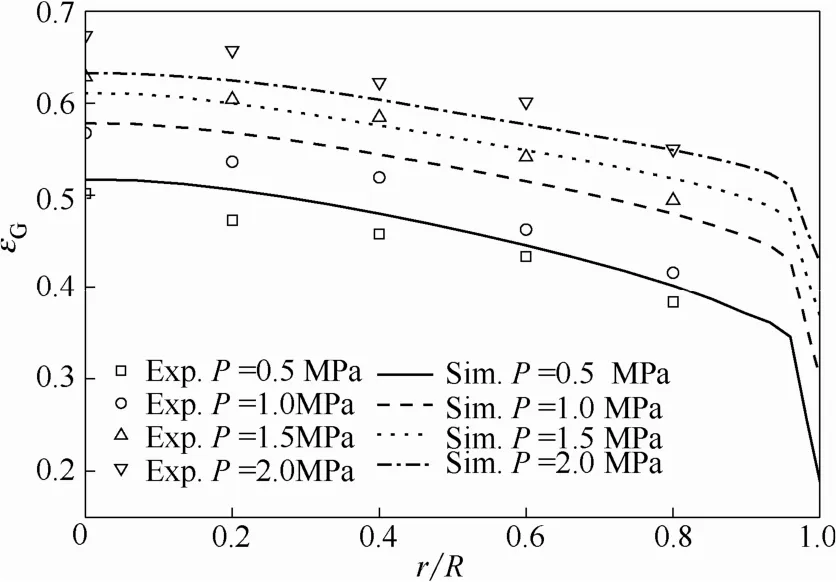
圖10 壓力對氣含率徑向分布的影響Fig.10 Effect of operating pressure on radial gas holdup distribution（VG=0.27 m·s?1, H=2.6 m）

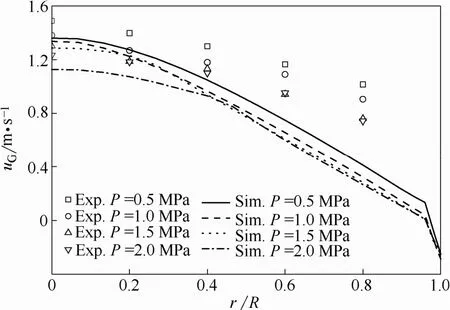
圖11 壓力對軸向氣速分布的影響Fig.11 Effect of operating pressure on gas rising velocity radial distribution（VG=0.27 m·s?1）

4 結 論

（1）本文采用雙流體模型對內徑0.3 m加壓湍動鼓泡塔內的氣液兩相流動，進行了動態二維軸對稱數值模擬。針對加壓條件下，采用改進的氣泡群曳力系數關聯式，同時考慮氣泡群徑向力平衡機制，以及壁面潤滑力建立的加壓鼓泡塔流體力學模型，數值計算的穩定性和效率較高，模擬得到的氣含率分布與實驗結果符合較好，能夠描述加壓鼓泡塔內氣含率和軸向氣速分布隨操作條件變化的趨勢。

（2）與其他采用單氣泡曳力系數的模型相比，改進的氣泡群曳力模型能夠較為準確地模擬加壓鼓泡塔總體氣含率和氣含率分布，正確描述軸向氣速分布隨表觀氣速和壓力的變化趨勢。對處于加壓湍動鼓泡狀態的工業漿態床反應器內流場特性參數分布的預測和變化規律的認識具有重要意義。

符 號 說 明

CD——曳力系數

CD,0——單氣泡曳力系數

CWL——壁面潤滑力系數

CTD——湍流擴散力系數

D——塔徑，m

dB——氣泡直徑，m

Fex——相間作用力，N·m?3

FL——氣泡升力，N·m?3

FTD——氣泡湍流擴散力，N·m?3

FWL——氣泡壁面潤滑力，N·m?3

g——重力加速度，m·s?2

H——軸向高度，m

k, kL——湍流動能, m2·s?2

Nc——計算網格數量

nW——指向壁面外的單位法向量

P——壓力，Pa

P0——標況下大氣壓，Pa

R——塔半徑，m

r——徑向位置，m

u——氣相或液相速度，m·s?1

uG——氣相速度，m·s?1

uL——液相速度，m·s?1

VG——表觀氣速，m·s?1

yw——壁面距離，m

ε——湍流耗散率，m2·s?3

εG——局部氣含率

εL——局部液含率

ε?G——平均氣含率

ε?L——平均液含率

μt——湍流黏度，Pa·s

ρG——氣體密度，kg·m?3

ρL——液體密度，kg·m?3

σ——液體表面張力，N·m?3

下角標

G——氣相

L——液相

i——液相(1)或氣相(2)

[1]許世峰, 王斯民, 李彩霞, 等. FT合成漿態床反應器的研究進展[J]. 化工進展, 2013, 32(S1): 4-8.XU S F, WAMG S M, LI C X, et al. Recent advances of the slurry-bed reactor FT synthesis[J]. Chemical Industry and Engineering Progress, 2013, 32(S1): 4-8.

[2]KRISHNA R,VAN BATEN J M. Eulerian simulations of bubble columns operating at elevated pressures in the churn turbulent flow regime[J]. Chemical Engineering Science, 2001, 56(21): 6249-6258.

[3]CHEN P, DUDUKOVIC M P, SANYAL J. Three-dimensional simulation of bubble column flows with bubble coalescence and breakup[J]. AIChE Journal, 2005, 51(3): 696-712.

[4]JOSHI J B. Computational flow modeling and design of bubble column reactors[J]. Chemical Engineering Science, 2001, 56: 5893-5933.

[5]TABID M V , ROY S A, JOSHI J B. CFD simulation of bubble column—an analysis of interphase forces and turbulence models[J]. Chemical Engineering Journal, 2007, 139(3): 589-614.

[6]LUCAS D, KREPPER E, PRASSER H M. Prediction of radial gas profiles in vertical pipe flow on the basis of buble size distribution[J]. International Journal of Thermal Sciences, 2001, 40(3): 217-226.

[7]張煜, 李紅波, 李兆奇, 等. 湍動漿態床流體力學研究(Ⅳ): 帶垂直列管束的漿態床流體力學模型與模擬[J]. 化工學報, 2011, 62(12): 3373-3380. ZHANG Y, LI H B, LI Z Q, et al. Hydrodynamics of turbulent slurry bubble column (Ⅳ): Modeling and simulation of bubble column with internal pipe bundles[J]. CIESC Journal, 2011, 62(12): 3373-3380.

[8]李兆奇, 王麗軍, 管小平, 等. 基于徑向力平衡的鼓泡塔二維流體力學模型[J]. 化工學報, 2014, 65(11):4221-4230. LI Z Q, WANG L J, GUAN X P, et al. 2-D hydrodynamic model of bubble column based on lateral-force balance[J]. CIESC Journal, 2014, 65(11): 4221-4230.

[9]DREW D A. Mathematical modeling of two-phase fow[J]. Annual Review of Fluid Mechanics, 1983, 15(1): 261-291.

[10]RAFIQUE M, CHEN P, DUDUKOVI? M P. Computational modeling of gas-liquid flow in bubble column[J]. Reviews in Chemical Engineering, 2004, 20(3): 225-375.

[11]DREW D A, PASSMAN S L. Applied Mathematical Sciences[M]. New York: Springer, 1999.

[12]PFLEGER D, BECKER S. Modeling and simulation of the dynamic flow behaviour in a bubble column[J]. Chemical Engineering Science, 2001, 56(4): 1737-1747.

[13]MUDDE R F, SIMONIN O. Two and three dimensional simulation of a bubble plume using a two fluid model[J]. Chemical Engineering Science, 1999, 54(21): 5061-5069.

[14]BUWA V V, RANADE V V. Dynamics of gas iquid flows in rectangular bubble columns: experiments and single/multi groups imulations[J]. Chemical Engineering Science, 2002, 57(22): 4715-4736.

[15]PFLEGER D, GOMES S, GILBERT N, et al. Hydrodynamic simulation of laboratory scale bubble columns, fundamental studies of Eulerian-Eulerian modeling approach[J]. Chemical Engineering Science, 1999, 54(21): 5091-5099.

[16]李光, 楊曉鋼, 戴干策. 鼓泡塔反應器氣液兩相流 CFD數值模擬[J]. 化工學報, 2008, 59(8): 1954-1965. LI G, YANG X G, DAI G C. CFD simulation of gas-liquid flow in bubble column[J]. Journal of Chemical Industry and Engineering (China), 2008, 59(8): 1954-1965.

[17]李光. 鼓泡塔反應器氣液兩相流數值模擬模型及應用[D]. 上海:華東理工大學, 2010. LI G. Two-phase flow dynamical simulations and modelling of bubble column reactors[D]. Shanghai: East China University of Science and Technology, 2010.

[18]KHOPKAR A R, RAMMOHAN A R, RANADE V V, et al. Gas-liquid flow generated by a Rushton turbine in stirred vessel: CARPT/CT measurements and CFD simulation[J]. Chemical Engineering Science, 2005, 60: 2215-2229.

[19]LAU Y M, ROGHAIR I, DEEN N G, et al. Numerical investigation of the drag closure for bubbles in bubble swarms[J]. Chemical Engineering Science, 2011, 66(14): 3309-3316.

[20]ROGHAIR I VAN SINT ANNALAND M, KUIPERS H J A M. Drag force and clustering in bubble swarms [J]. AIChE Journal, 2013, 59(5): 1791-1800.

[21]秦玉建. 加壓氣液鼓泡塔流體參數的測量與CFD數值模擬[D]. 北京: 北京化工大學, 2012. QIN Y J. The measurement of hydrodynamic parameters and CFD simulation of gas-liquid flow behaviors in a pressurized bubble column[D]. Beijing: Beijing University of Chemical Technology, 2012.

[22]DREW D A, LAHEY R T. In Particulate Two-phase Flow[M]. Boston: Butterworth Geinemann, 1993: 509-566.

[23]LOPEZ DE BERTODANO M. Turbulent bubbly two-phase flow in a triangular duct [D]. New York: Rensselaer Rolytechnic Institute, 1992.

[24]ANTAL S P, LAHEY JR R T, FLAHERTY J E. Analysis of phase distribution in fully developed laminar bubbly two-phase flow[J]. Int. J. Multiphase Flow, 1991, 17(5): 635-652.

[25]TOMIYAMA A. Struggle with computational bubble dynamics[C]// ICMF'98, 3rd International Conference on Multiphase Flow. Lyon, France, 1998: 1-18.

Hydrodynamics simulation of pressurized bubble column based on bubble swarm interphase force models

LIU Xin1,2, ZHANG Yu2, ZHANG Li2, JIN Haibo1
(1School of Chemical Engineering, Beijing Institute of Petrochemical Technology, Beijing 102617, China;2Research and Development Center, Synfuels China, Beijing 101407, China)

The commercial bubble column reactors are normally operated under the conditions of pressurized state and churn turbulent bubbly flow which the superficial gas velocity always exceeded 0.1 m·s?1. However, most of the published literatures are focus on the cold model experimental investigation of the flow field characteristics in pressurized churn-turbulent bubble columns, and the empirical or semi-empirical correlations which were on the basis of the cold model experimental data to quantitatively estimate the characteristic parameters. Therefore, it is lack of the systematic study on the flow characteristics in the pressurized turbulent bubble columns by the hydrodynamic models with interactions between bubbles and liquid phase. In this work, a steady 2-D axisymmetric hydrodynamic two-fluid model of pressurized bubble column was developed on the platform of FLUENT 15.0 with the UDF sub-models which described the bubble swarm interface forces. The numerical investigations upon the flow field characteristics of pressurized churn turbulent bubble column with the operation pressure varying from 0.5 MPa to 2.0 MPa, and superficial gas velocity from 0.2 m·s?1to 0.31 m·s?1were performed. Moreover, the comparisons between the simulation results and cold model experimental data were implemented. The comparisons indicated that, the model with the bubble swarm interface forces including improved bubble swarm drag force model, lateral force balance model, and wall lubrication force model, is able to reflect the influences of operation pressure and superficial gas velocity upon flow pattern, that is, the elevatingoperation pressure leads to increase of time averaged gas holdup and decrease of time averaged axial gas phase velocity, whereas for the ascending superficial gas velocity, the gas holdup and gas phase velocity are both raising. Consequently this mathematical model could correctly predict the basic gas-liquid flow pattern in the turbulent pressurized bubble columns, and simulation results are in good agreement with the experimental data.

bubble column; gas-liquid flow; computational fluid dynamics; bubble swarm drag force model; lateral- force balance model; wall lubrication force model

Prof. JIN Haibo, jinhaibo@bipt.edu.cn

TQ 021.1

：A

：0438—1157（2017）01—0087—10

10.11949/j.issn.0438-1157.20160762

2016-06-01收到初稿，2016-10-20收到修改稿。

聯系人：靳海波。

：劉鑫（1989—），男，碩士研究生。

國家自然科學基金重大研究計劃項目（91634101）；北京市屬高等學校高層次人才引進與培養計劃項目（CIT&TCD20130325）。

Received date: 2016-06-01.

Foundation item: supported by the National Natural Science Foundation of China (91634101) and the Importation and Development of High-Caliber Talents Project of Beijing Municipal Institutions(CIT&TCD20130325).