預測視角下雙因子模型與高階模型的模擬比較*

徐霜雪 俞宗火 李月梅

(江西師范大學心理學院,南昌 330022)

1 引言

心理學研究中的概念常常由多個相互聯系的維度或層面構成,每個維度或層面又由若干個子維度或層面構成。比如,根據中國人大七人格理論,人格特質包含外向性、善良、情緒性、才干、人際關系、行事風格以及處事態度等7個維度。其中,外向性又包含合群、活躍和樂觀;善良包含真誠、利他和重感情等等(王登峰,崔紅,2005)。傳統上,我們習慣于采用高階因子模型來對這些概念進行表征。近年來,雙因子模型(Bi-factor Model)則受到越來越多的關注(Jennrich &Bentler,2012;Rodriguez,Reise,&Haviland,2016),被廣泛地應用于人格心理學(Chen,Hayes,Carver,Laurenceau,&Zhang,2012;顧紅磊,溫忠麟,方杰,2014;Hyland,Boduszek,Dhingra,Shevlin,&Egan,2014;Reise,Moore,&Haviland,2010;黎志華,尹霞云,蔡太生,朱翠,2013)、能力測驗(Gillmore &Hawkins,1991)、管理心理學(Howard,Gagné,Morin,&Forest,2016)和心理健康(Chen,Jing,Hayes,&Lee,2013;Reise,Morizot,&Hays,2007)等心理學領域。

雙因子模型有著很長的歷史(Holzinger &Swineford,1937;Spearman,1927),近年來重拾關注,很大程度上是作為高階因子模型的競爭模型被提出(Chen et al.,2012,2013;Chen,West,&Sousa,2006;Rindskopf &Rose,1988;Yung,Thissen,&McLeod,1999)。這些研究主要關注兩個模型在擬合方面的比較。基于實測數據或在實測數據基礎上的模擬研究,幾乎是一邊倒地認為雙因子模型優于高階因子模型(Chen et al.,2006,2012,2013;Morgan,Hodge,Wells,&Watkins,2015;Reise,2012),但也有模擬研究并未發現兩者有顯著差異(Mulaik &Quartetti,1997)。實際上,拋開實測數據,單純從數理上分析,雙因子模型與高階因子模型具有嵌套關系,后者嵌套于前者(Yung et al.,1999),在滿足比例約束的條件下,二者是等價的(Schmid &Leiman,1957)。雙因子模型的優點主要體現在探討局部因子的作用時,可以通過局部因子的負荷直接判斷其作用大小(Chen et al.,2006;Reise et al.,2010);然而,相對于高階因子模型而言,雙因子模型也有其不足：模型更加復雜,需要估計的參數更多,在小樣本條件下,有時需要提供初始值才能收斂(Chen et al.,2006)。就模型擬合而言,盡管各項研究之間結果頗不一致,大體上還是可以認為：兩者即便在個別擬合指標上差異顯著,實際差異也很小,而且兩個模型都能達到擬合良好的標準(Chen et al.,2006;Morgan et al.,2015;Mulaik &Quartetti,1997;顧紅磊等,2014)。因此,目前還很難判斷,基于實測數據得出的結論,究竟是體現了雙因子模型與高階因子模型的本質差異,還是在特定情況下才會偶爾出現的偏差(Borenstein,Hedges,Higgins,&Rothstein,2009)。

除了模型擬合指標,預測效度也是模型結構效度的重要方面。然而,到目前為止,尚沒有對這兩個模型的預測效度進行比較的系統研究。預測效度反映了測驗得分能夠準確預測效標分數的程度(Cronbach &Meehl,1955)。在結構方程模型中,預測效度可以通過結構系數來度量。在實際應用中,結構效度高的模型,其預測效度未必會高(Aiken,2005/2011)。因此,在兩個模型的擬合指標“不相上下”的情況下,從預測效度這一視角出發,對高階因子模型和雙因子模型進行比較,具有非常重要的理論和實踐意義。而且,由于結構方程中結構系數的估計容易出現偏差(Muthén,Kaplan,&Hollis,1987),而高階因子模型更為簡潔,參數估計方面比雙因子模型更具優勢(Chen et al.,2006;顧紅磊等,2014),因此,在估計結構系數時,高階因子模型可能會比雙因子模型更加準確。但是,以往基于實測數據的研究無法知道真值所在,不利于開展預測效度的比較研究。只有模擬研究才知道結構系數的真值是多少,進而對結構系數偏差進行評估。

作為衡量測驗有效性的外在標準,效標既可以是工資績效等外顯變量,也可能是積極情緒、自尊等內潛變量(Chen et al.,2012)。由于對人心理的測量具有間接性的特點,所以,大多心理學變量都是內潛變量。若這些內潛變量的得分僅僅是各個題目得分的簡單相加,則會存在很多缺陷(顧紅磊等,2014)。所以,Reise,Scheimes,Widaman和Haviland(2013)通過對效標潛變量的運用來評估用單維結構來測量多維心理學構念帶來的結構系數偏差的大小。Muthén等人(1987)認為,結構系數偏差更可能發生在潛變量模型中。因此,我們預期,相對于效標變量為顯變量的情況,當效標變量為潛變量時,結構系數偏差可能會更大。

鑒于上述原因,本研究擬通過Monte Carlo模擬比較,在模型擬合差異比較的基礎上,對效標分別為顯變量和內潛變量時,不同負荷水平條件下的雙因子模型和高階因子模型的預測效度進行了系統的比較。

2 模型概述

2.1 雙因子模型

雙因子模型,也被稱為全局?局部模型(generalspecial model)或嵌套模型(nested model),它是用一個全局因子(general factor)來解釋所有題目的共同變異,同時用多個局部因子(special factor)來反映各維度的獨特性(Chen et al.,2012);早期雙因子模型僅在智力研究領域中有應用(Spearman,1927),近年來在人格心理學、健康心理學和管理心理學等研究領域中也逐漸得到了重視(如,Howard et al.,2016;Musek,2007;Reise et al.,2007)。雙因子模型假定：(1)用一個全局因子解釋所有題目的共同變異,(2)存在多個局部因子,控制全局因子的影響后,每個局部因子可以額外解釋部分題目的共同變異。圖1中的M為一個雙因子模型的示意圖,M中彎曲的雙箭頭代表著每個潛變量因子的方差以及每個觀測變量測量誤差的方差。假設向量Y、Λ、η和ε分別代表觀測變量向量、全局因子和局部因子的因子負荷、全局和局部因子以及殘差;觀測變量可用以下公式來表達：

其中,公式(1)中等號右邊第一項代表了全局因子和局部因子的貢獻,第二項代表殘差。值得注意的是,雙因子模型中全局因子與局部因子之間是正交關系。公式(1)的數學展開式見電子版附錄1。

2.2 高階因子模型

圖1 雙因子模型與高階因子模型示意圖

高階因子模型的表達式如下：

公式(2)代表各個低階因子的結構,公式(3)代表觀測變量的測量方程。展開后的公式見電子版附錄1。

2.3 預測效度的判斷標準與比較

從預測效度的角度來說,對一個好的模型,研究者所關心的心理學變量與效標之間的相關系數或回歸系數,必然是對真值的無偏估計。因此,本文采用結構系數偏差(structural coefficient bias,也被稱為效度系數)來評價模型的預測精準度,它是指預先設定的或總體的結構系數與估計的結構系數之差的絕對值除以所設定的結構系數所得的百分比,也即模型所估計出的結構系數與之前設定的結構系數偏離的程度(Muthén et al.,1987)。稍早的文獻認為,結構系數偏差少于 10%～15%時,偏差可以忽略,視為無偏估計(Bandalos,2002;Muthén et al.,1987)。但 Reise等人(2013)認為,偏差超出10%,誤差就很嚴重了。所以,Reise等人提出將10%作為閾值來判斷結構系數是否為無偏估計,本研究沿用Reise等人的標準來對模型預測精準度進行評判。

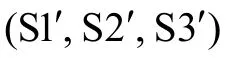
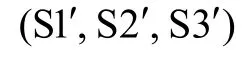
結合高階因子模型與雙因子模型的預測圖可知,雙因子模型的結構系數偏差,可通過計算全局因子與局部因子對效標變量的預測系數的估計值偏離真值的程度得出;同樣地,高階因子模型中的高階因子的結構系數偏差也可直接通過高階因子的預測系數的估計值對真值的偏離程度來計算,而低階因子的結構系數是低階因子的殘差對效標的預測系數,其偏差為相應的預測系數的估計值對真值的偏離程度。

圖2 雙因子模型及高階因子模型預測圖

在進行模型指定時,直接用低階因子的殘差去預測效標變量,即殘差回歸方法(residual regression model) (Chen et al.,2012)。這種方法所蘊含的原理是由 Gustafsson和 Balke (1993)提出的,即將低階因子的方差固定為 0,低階因子的殘差對低階因子的負荷固定為 1。此時,與雙因子模型中各局部因子的效應相對應,低階因子的效應即可轉化為低階因子的殘差在低階因子上的負荷估計值與低階因子在各觀測變量上的負荷估計值的乘積,低階因子的殘差轉化成因子的形式,對效標變量進行預測,其回歸系數即為高階因子模型中低階因子對效標變量的結構系數,其結構系數偏差為殘差對效標變量的預測系數的估計值偏離真值的程度。例如,當全局因子為0.7,局部因子為0.7時,高階因子模型中低階因子的殘差對低階因子的負荷估計值為0.752(某次實驗時的模型估計值),低階因子在觀測變量Y1上的負荷估計值為0.989,高階因子在低階因子上的負荷估計值為 0.659,此時,低階因子的殘差對觀測變量 Y1的效應為 0.752×0.989=0.7437 (相當于雙因子模型中局部因子負荷的估計值,約為 0.7),此時,低階因子的殘差就可以直接對效標變量進行預測,且可通過估計出的預測系數直接計算出結構系數偏差的大小。

雙因子模型對外部效標變量的預測作用,主要表現在全局因子和局部因子可以單獨對外部效標變量進行預測,且局部因子對效標變量的預測作用是在控制了全局因子的作用之后。這是因為雙因子模型中,全局因子與各局部因子之間是相互獨立的。同樣地,高階因子模型中局部因子對效標變量的預測作用,表現在模型中低階因子的殘差與高階因子也是相互獨立的。所以,高階因子模型的局部因子和全局因子可以同時對外部效標變量進行預測。這樣,兩個模型之間的預測效度就可以直接進行比較。

3 研究1 效標為顯變量時,雙因子模型與高階因子模型比較

3.1 研究方法

為了更好地模擬現實情境,研究設置了不同負荷水平。在不同負荷水平下,比較雙因子模型與高階因子模型的擬合效果差異以及效標為顯變量時兩個模型的預測效度差異。模擬程序主要有以下幾個步驟：

(1) 用Monte Carlo模擬的方法,按照雙因子模型(高階因子模型)下相應的參數值,導出方差?協方差矩陣,由矩陣出發產生隨機數據。按照 Schmid-Leiman轉換方法可將雙因子模型的參數值和高階因子模型的參數相對應起來,此時方差?協方差矩陣也相當于是由高階因子模型相應參數值而導出。其中,雙因子模型中全局因子的負荷是高階因子模型中低階因子負荷與高階因子負荷的乘積,而局部因子的負荷則為低階因子在觀測變量上的負荷與低階因子的殘差在低階因子上的負荷的乘積。

模型中參數的取值主要是全局因子和局部因子的負荷水平值,全局因子分別有0.4,0.5,0.6,0.7,局部因子分別有0.4,0.5,0.55,0.6,0.7,這些負荷水平值都是標準化路徑系數。參數的設定參考 Reise等人(2013)對雙因子模型的參數設定,與 Reise等人對雙因子模型的參數設定不同的是,本研究不予考慮路徑系數為0.3及0.3以下的值,因為路徑系數少于0.3的項目的路徑系數不符合實證研究中好的結構效度模型應有的路徑系數要求。另外,限定路徑系數的最高取值(0.7)是為了避免全局因子和局部因子對觀測變量所解釋的方差大于等于1的情況(若觀測變量在G因子上的負荷為0.8,同時觀測變量在 3個 S因子上的負荷也為0.8,則每個觀測變量被G因子和S因子共同解釋的方差為0.8+0.8=1.28>1)。被試人數固定為 1000。所有實驗條件下,雙因子模型只有1個全局因子,3個局部因子,且每個因子都在 4個觀測變量上有因子負荷(見圖2中的 M)。其中,每種情況下所有觀測變量全局因子上的因子負荷相等,觀測變量在3個局部因子上的因子負荷也都取相同的值。這樣設置總體模型(population model)方法是源自于 Holzinger和Swineford (1937)的嚴格的(“strictly”)雙因子模型設定——每個項目都在全局因子和一個且僅一個局部因子上有負荷,所有因子間正交。此時,實驗條件有 4×4=16種情況。此外,為了避免 3個局部因子上的因子負荷相同可能帶來的不切合實證研究的情況產生。本研究還在此基礎上增加了一種實驗條件,即全局因子負荷取不同負荷水平的值(0.4,0.5,0.6,0.7)的情況下,3個全局因子上的因子負荷都分別為0.4,0.55,0.7,其中0.55為0.4和0.7的中間值。最后,實驗條件有16+4=20種情況。

(2) 在第一步的基礎上增加一個效標觀測變量,指定全局因子和3個局部因子對效標觀測變量的預測系數都為0.3,所以總共有13個觀測變量,所有變量都服從標準正態分布。所以,最后有20種實驗條件下所產生的數據,每種實驗條件重復100次。

(3) 用雙因子模型擬合所產生的數據,并指定全局因子和局部因子對效標觀測變量的回歸路徑。

(4)用高階因子模型擬合所產生的數據,指定全局因子和低階因子的殘差對效標觀測變量的回歸路徑。

(5) 對于雙因子模型與高階因子模型在擬合效果方面的差異比較,評價指標主要采用D

x

值,CFI,SRMR以及RMSEA。而對于兩個模型預測效度的比較,本研究采用結構系數偏差來進行比較。其中,所有實驗條件下的模型擬合指數和結構系數估計值的最終結果取100次模擬實驗結果的平均值。

所有模擬過程使用EQS 6.2編寫程序,并使用極大似然估計方法,程序代碼見電子版附錄2。

3.2 研究結果

3.2.1 模型擬合效果比較

表1列出了不同全局因子及局部因子負荷水平下,雙因子模型與高階因子模型的擬合指數。在所有20種實驗條件下,100次重復實驗結果都顯示擬合成功,無擬合失敗的情況。總體來看,每種實驗條件下,雙因子模型與高階因子模型的CFI指數都在 0.99以上,RMSEA指數和 SRMR指數也都在0.05以下。這說明每種實驗條件下,雙因子模型和高階因子模型都很好地擬合了數據;此外,相比較而言,兩個模型在CFI、SRMR和RMSEA等指標上的差異都非常小,很難說是否達到統計顯著水平,從兩個模型的似然比卡方檢驗結果來看(表1中的

p

值),都未達到顯著水平。綜上所述,兩個模型對數據都有很好的擬合效果,而且,在擬合效果方面并無顯著差異。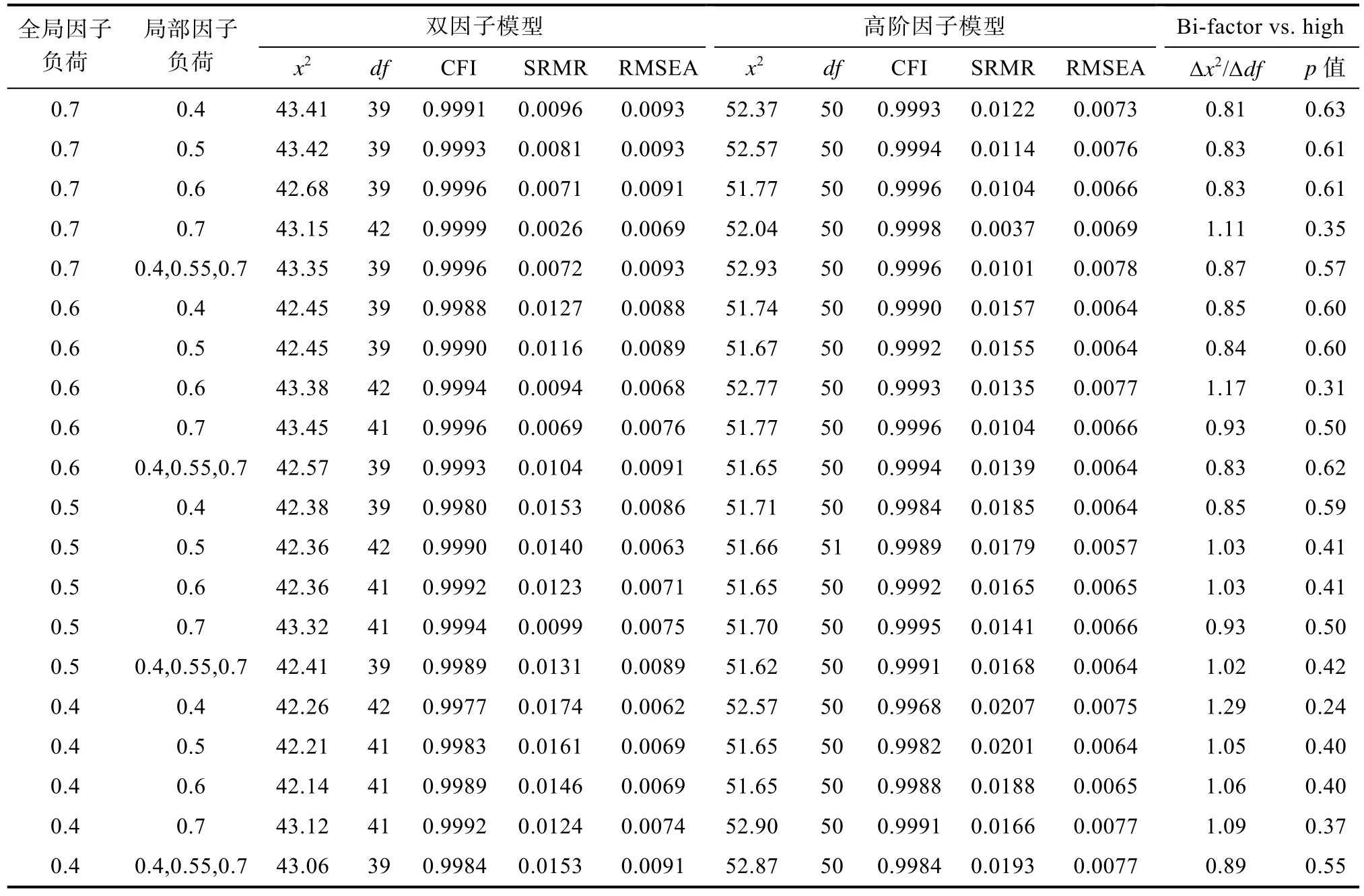

表1 雙因子模型與高階因子模型的擬合指數

3.2.2 不同負荷水平下兩個模型對外部效標觀測變量的預測效度比較

增加效標觀測變量以后,全局因子和局部因子對效標觀測變量的預測系數即為結構系數。其中,圖2中 M和M的 a1、a2、a3分別為雙因子模型的3個局部因子以及高階因子模型的3個低階因子的殘差對效標觀測變量的預測系數的估計值,b為全局因子和高階因子對效標觀測變量的預測系數的估計值。那么,雙因子模型中全局因子的結構系數偏差的計算公式為：abs(b?0.3)/0.3,而局部因子S1的結構系數偏差的計算公式為：abs(a1?0.3)/0.3;不同于雙因子模型直接利用結構系數計算偏差,高階因子模型中低階因子的結構系數偏差的計算是通過低階因子的殘差對效標觀測變量的預測系數的估計值計算出。如圖2的M中,a1、a2、a3分別為低階因子的殘差對效標觀測變量的預測系數的估計值,那么低階因子S1的結構系數偏差為：abs(a1?0.3)/0.3,而高階因子的結構系數偏差可直接通過高階因子的結構系數計算,即abs(b?0.3)/0.3。結構系數偏差能夠反映出模型預測效度的好壞,此處沿用上文中 Reise等人(2013)提出的標準,即結構系數偏差不大于10%時,估計的結構系數被視為是無偏的,否則,便是有偏估計。

表2為不同全局因子及局部因子負荷水平下,雙因子模型與高階因子模型中全局因子(G)和局部因子(S1/S1￠,S2/S2￠,S3/S3￠)對效標觀測變量的回歸系數偏離真值(0.3)的百分比,即結構系數偏差。由表2可知,所有實驗條件下,雙因子模型的全局因子和局部因子的結構系數偏差大部分都控制在了10%以內,只有一個值在 10%以上,即當全局因子負荷為0.7,局部因子負荷為0.6時,全局因子對效標變量的結構系數偏差為 13.025%,這表明除了這個值以外,對雙因子模型的結構系數的估計可視為是無偏的;與之相對應地,高階因子模型的高階因子和低階因子殘差的結構系數偏差也都在 10%以內,也有一個值是在10%以外(12.153%),此時也是全局因子負荷為0.7,局部因子負荷為0.6時。雖然兩個模型各有一個值越界,但這種現象在整個模擬結果中發生的概率是1/80,可以被看作是一個小概率事件,這說明雙因子模型和高階因子模型的預測系數都可以被認為是無偏估計。

由兩個模型的預測效度的結果可知,雙因子模型和高階因子的全局因子和局部因子都可以單獨對外部效標觀測變量進行預測,且兩個模型的效度系數都為無偏估計,二者的預測系數估計值也類似。

表2 效標為顯變量時雙因子模型與高階因子模型的結構系數偏差

4 研究2 效標為潛變量時,兩個模型的預測效度比較研究

4.1 研究方法

此處的模型參數設置與3.1中雙因子模型下觀測變量在全局因子與局部因子上的參數設置相同,只是將效標觀測變量變為潛變量,其中潛變量Criterion是由3個觀測變量(X1,X2,X3)抽取出的潛變量,且3個路徑系數的參數都設為0.7。這樣設置效標潛變量上因子負荷值的方法也是參考Reise等人(2013)設置效標測量模型的原則(3條路徑系數分別為0.6,0.65,0.7),然而本研究為了計算的方便,3條路徑系數都取值為 0.7,這樣也代表著一個好的(“good”)測量模型。同樣地,指定全局因子和 3個局部因子對效標潛變量的預測系數都為0.3。這樣,模擬生成的變量就有 15個(其中包括模型中的 12個變量以及 3個觀測變量),所有變量都服從標準正態分布。通過變化負荷(參見研究 1)）,得到 20種實驗條件,每種實驗條件下重復100次。對于雙因子模型與高階因子模型在擬合效果方面的差異比較,研究 1中已有說明,此處不再贅述。而對于兩個模型預測效度的比較,此處仍采用結構系數偏差做指標。

4.2 研究結果

表3列出了不同全局因子及局部因子負荷水平下,雙因子模型與高階因子模型中全局因子(G)和局部因子(S1/S1￠,S2/S2￠,S3/S3￠)對效標潛變量的回歸系數偏離真值(0.3)的程度,即結構系數偏差。此處雙因子模型與高階因子模型的結構系數偏差計算方式與研究1相同。

由表3可知,高階因子模型中,所有實驗條件下,高階因子和低階因子的殘差對效標潛變量的回歸系數偏差都在10%以內。這說明當效標變量為潛變量時,高階因子模型在所有實驗條件下的預測效度都很好,各個因子對效標潛變量的預測系數也都屬于無偏估計。雙因子模型中,有 9種情況下,全局因子和局部因子對效標潛變量的回歸系數偏差在 10%以內,此時結構系數屬于無偏估計。但是,有 11種情況下,雙因子模型的結構系數偏差都在10%以上：(1)當全局因子水平為0.7,局部因子水平分別為 0.6和 0.7時,雙因子模型中全局因子和 3個局部因子的結構系數偏差都大于15%;(2)當全局因子水平為 0.6,局部因子水平為 0.5以及分別為0.4,0.55,0.7時,各因子對效標變量的結構系數偏差也大于 10%;(3)當全局因子水平為 0.5,局部因子水平為0.4、0.5、0.6以及分別為0.4,0.55,0.7時,結構系數偏差也大于 10%;(4)當全局因子水平為0.4,局部因子水平分別為0.4、0.5以及分別為0.4,0.55,0.7時,結構系數偏差也大于10%。其中,20種實驗條件下,雙因子模型的結構系數偏差大于高階因子模型的結構系數偏差的次數有 13次,而高階因子模型的結構系數偏差大于雙因子模型的結構系數偏差只有1次。上述結果表明雙因子模型的結構系數偏差在 50%左右的情況下都在 10%以上,說明此時雙因子模型的結構系數估計值為有偏估計,高階因子模型的預測效度有一半左右的情況下是優于雙因子模型的。

由上述結果可知,效標為潛變量時,模型變得較為復雜,此時雙因子模型和高階因子模型的結構系數偏差普遍大于效標為觀測變量時二者的結構系數偏差。這也印證了 Muthén等人(1987)的觀點,即潛變量模型中更容易出現結構系數偏差。此外,雙因子模型的結構系數偏差大于高階因子的結構系數偏差的次數較多,說明此時高階因子模型的預測效度相對好于雙因子模型。

為了檢驗樣本對研究結果的影響,我們還檢驗了樣本容量為200和500時的情況(參見電子版附錄3和4)。結果顯示,所有實驗條件下(即

N

=200及500時),兩個模型都擬合良好,且并無顯著差異。但在預測效度方面,高階因子模型總體上都要好于雙因子模型,這個趨勢和

N

=1000時的結果是一樣的,這也證明了這一結果的穩健性。此外,當

N

=200時,無論效標變量為顯變量還是潛變量,高階因子模型和雙因子模型的結構系數偏差都比

N

=1000時的更大,而當

N

=500時,高階因子模型和雙因子模型的結構系數偏差比

N

=200時要小,但仍大于

N

=1000時的結構系數偏差。這說明隨著樣本容量的增大,模型的結構系數偏差會變小。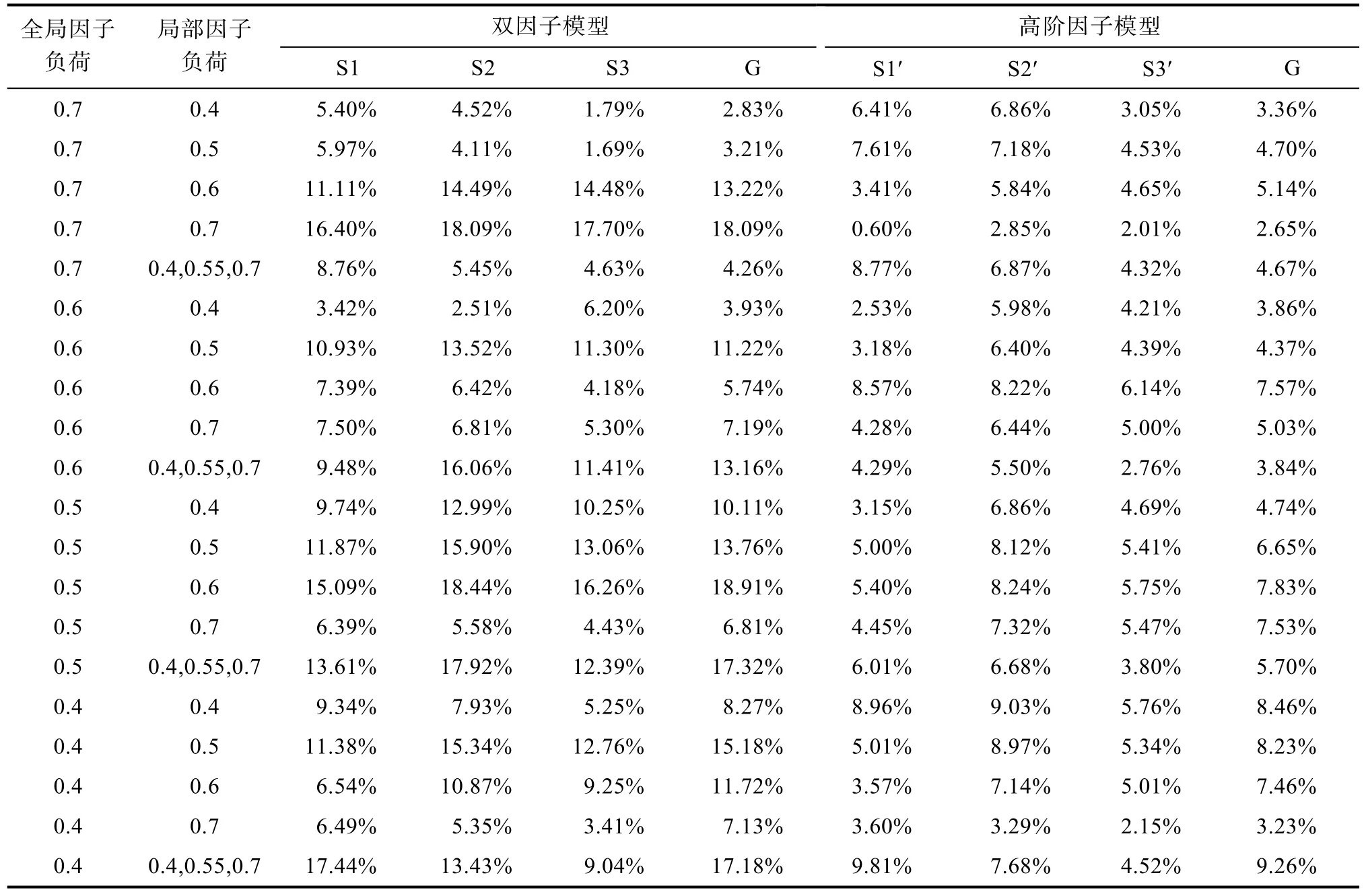

表3 效標為潛變量時雙因子模型與高階因子模型的結構系數偏差

5 結論

本研究比較了不同負荷條件下,雙因子模型與高階因子模型在擬合效果和預測效度方面的差異,并通過模擬研究得到以下結論：

(1) 就模型擬合效果的比較而言,雙因子模型與高階因子模型在不同的負荷條件下都較好地擬合了所產生的數據,且二者并無顯著差異。

(2) 對于兩個模型預測效果的比較來說,當效標為顯變量時,雙因子模型與高階因子模型的結構系數估計值的偏差皆僅有一次超過10%,發生概率為1/80,可以認為,兩個模型都屬于無偏估計。

(3) 當效標為潛變量時,高階因子模型的結構系數偏差全都小于10%,而雙因子模型中有50%左右的結構系數偏差大于10%。

綜上,我們認為,相對于高階因子模型而言,雙因子模型的優勢主要體現在可以通過局部因子的負荷直接判斷其作用大小(Chen et al.,2006;Reise et al.,2010),但在模型擬合方面,并沒有優勢,而且,在用全局因子和局部因子預測潛變量時,高階因子模型更具優勢。

6 討論與展望

雙因子模型和高階因子模型不僅廣泛應用于心理學的各個研究領域,在管理學等其他學科領域也有廣泛的應用。本研究在不同負荷水平下對兩個模型的擬合優度和預測效度進行了系統的比較,并在兩個方面拓展了現有的知識,因而,本研究具有非常重要的理論和實踐意義。

首先,研究結果表明,雙因子模型與高階因子模型在擬合效果上并無顯著差別,這與 Mulaik和Quartetti (1997)的模擬實驗研究的結果是一致的,但是其研究只是針對特定負荷條件下的兩個模型進行了比較,并未涉及到多種負荷條件下的情況,缺乏一般性。相較之下,本研究的進步之處在于比較了不同負荷條件下的模型表現,更具拓廣性。Morgan等人(2015)的模擬研究顯示雙因子模型比高階因子模型有更好的擬合,但兩個模型在一些擬合指數上也有重疊的地方,且他們并未比較兩個模型的卡方值,無法對兩個模型進行差異檢驗。Chen等人(2006) 的實證研究則顯示雙因子模型的擬合在個別指標(卡方值)上要好于高階因子模型,國內也有少數幾個實證研究發現雙因子模型要優于高階因子模型,但這些研究大多表明：雖然二者的似然比卡方檢驗是顯著的,但二者的差別卻很小(Chen et al.,2012)。本研究在結合 Mulaik和Quartetti (1997)的研究以及Morgan等人(2015)研究的基礎上進一步增加了對兩個模型卡方值的比較,還增設了不同負荷條件下的情況。這樣,與實證研究相比,模擬研究就更加系統。模擬研究結果與實證研究結果之間的不一致,不排除實證研究存在偏差的可能(Borenstein et al.,2009),未來有必要在實證研究積累到一定量的基礎上進行元分析。此外,本研究對模型進行比較時所用的擬合指數,主要是傳統的擬合指數,近年來,有研究者開發出了適合雙因子模型的擬合指標(Rodriguez et al.,2016),未來有必要在這些指標上對兩個模型進行比較。

其次,本研究重點考察了效標為顯變量和潛變量時,雙因子模型和高階因子模型預測效度的情況。發現當效標為顯變量時,研究結果表明兩個模型的預測系數都為無偏估計。相對于 Chen等人(2006)的研究,在預測系數方面,本研究有兩個方面的拓展：Chen等人的研究雖然發現雙因子模型和高階因子模型在預測顯變量效標時,二者的預測系數很接近,但基于實測數據的研究無法知道結構系數的真值所在,而本研究能夠清楚地說明兩個模型在預測因變量時偏差究竟有多大;另一個重要拓展是,Chen等人的研究,并未涉及到因變量為潛變量的情況。通過系統的模擬實驗,本研究發現,當效標變量為潛變量時,高階因子模型的結構系數偏差皆在 10%這一正常范圍之內;而雙因子模型,有50%左右的結構系數偏差高于10%這一閾限值。如果按照15%這一較為寬松的標準,仍然有16%左右的情況下結構系數存在偏差。這一結果證實了Muthén等人(1987)的觀點,即結構系數偏差常發生在潛變量模型中,甚至是潛變量模型的重要部分。此外,相對于高階因子模型,雙因子模型更為復雜,參數估計的難度更大(Chen et al.,2012;顧紅磊等,2014),這可能是雙因子模型在預測潛變量時,會有更大偏差的原因。

最后,以往有關高階因子模型和雙因子模型的研究主要集中在模型擬合比較方面,而科學研究與應用的目的在于對世界上的各種現象進行描述、解釋、預測和控制。本研究顯示,相對于雙因子模型而言,高階因子模型能對效標變量做出更加精準的預測,這有助于研究者對其所研究的現象進行更好的預測和控制。因此,本研究的實踐意義就在于研究者可以根據本研究的結論更客觀地評價兩個模型的優劣,并最終根據研究目的與模型的適配性來準確地選用模型,這樣才能更準確地揭示變量之間的因果關系。

雖然高階因子模型在預測潛變量時比雙因子模型更少發生偏差,雙因子模型還是有其存在的價值與意義的。首先,在高階因子模型中,局部因子與全局因子指向觀察變量的負荷是共用的,難以區分各部分的大小,不利于偵測出無意義的局部因子。而雙因子模型可以偵測出那些負荷較低且不顯著,或方差不顯著的局部因子,如果局部因子不顯著,此時說明局部因子沒有存在的必要,也就是說題目完全由全局因子來解釋(Chen et al.,2006)。其次,雖然研究結果顯示出高階因子模型在預測上有優勢,但是,高階因子模型的局部因子對外部效標變量的預測只能通過低階因子的殘差來進行,現有的大多數軟件并不能實現這一功能,目前已有的且較為簡單的可以實現這一功能的軟件只有EQS,這可能給那些用高階因子模型來做預測的實證研究者帶來不便。

Aiken,L.R.,&Groth-Marnat,G.(2011).

Psychological testing and assessment

(12th ed.).Boston:Allyn &Bacon.(Original work published 2005).[艾肯,格羅恩-馬納特.(2011).

艾肯心理測量與評估

(張厚璨,趙守盈 譯).北京:中國人民大學出版社.]Bandalos,D.L.(2002).The effects of item parceling on goodness-of-fit and parameter estimate bias in structural equation modeling.

Structural Equation Modeling:A Multidisciplinary Journal,9

(1),78?102.Bentler,P.M.(1995).

EQS 6 structural equations program manual.

Encino,CA:Multivariate Software.Borenstein,M.,Hedges,L.V.,Higgins,J.P.T.,&Rothstein,H.R.(2009).

Introduction to meta-analysis

.Chichester:John Wiley and Sons.Chen,F.F.,Hayes,A.,Carver,C.S.,Laurenceau,J.-P.,&Zhang,Z.G.(2012).Modeling general and specific variance in multifaceted constructs:A comparison of the bifactor model to other approaches.

Journal of Personality,80

(1),219?251.Chen,F.F.,Jing,Y.M.,Hayes,A.,&Lee,J.M.(2013).Two concepts or two Approaches? A bifactor analysis of psychological and subjective well-being.

Journal of Happiness Studies,14

(3),1033?1068.Chen,F.F.,West,S.G.,&Sousa,K.H.(2006).A comparison of bifactor and second-order models of quality of life.

Multivariate Behavioral Research,41

(2),189?225.Cronbach,L.J.,&Meehl,P.E.(1955).Construct validity in psychological tests.

Psychological Bulletin,52

(4),281?302.Gillmore,M.R.,Hawkins,J.D.,Catalano,R.F.,Jr.,Day,L.E.,Moore,M.,&Abbott,R.(1991).Structure of problem behaviors in preadolescence.

Journal of Consulting and Clinical Psychology,59

(4),499?506.Gu,H.L.,Wen,Z.L.,&Fang,J.(2014).Bi-factor models:A new measurement perspective of multidimensional constructs.

Journal of Psychological Science,37

(4),973?979.[顧紅磊,溫忠麟,方杰.(2014).雙因子模型:多維構念測量的新視角.

心理科學,37

(4),973?979.]Gustafsson,J.-E.,&Balke,G.(1993).General and specific abilities as predictors of school achievement.

Multivariate Behavioral Research,28

(4),407?434.Holzinger,K.J.,&Swineford,F.(1937).The bi-factor method.

Psychometrika,2

(1),41?54.Howard,J.L.,Gagné,M.,Morin,A.J.S.,&Forest,J.(2016).Using bifactor exploratory structural equation modeling to test for a continuum structure of motivation.

Journal of Management

,in press.Hull,J.G.,Lehn,D.A.,&Tedlie,J.C.(1991).A general approach to testing multifaceted personality constructs.

Journal of Personality and Social Psychology,61

(6),932?945.Hyland,P.,Boduszek,D.,Dhingra,K.,Shevlin,M.,&Egan,A.(2014).A bifactor approach to modelling the rosenberg self esteem scale.

Personality and Individual Differences,66

,188?192.Jennrich,R.I.,&Bentler,P.M.(2012).Exploratory bi-factor analysis:The oblique case.

Psychometrika,77

(3),442?454.Li,Z.H.,Yin,X.Y.,Cai,T.S.,&Zhu,C.Y.(2013).The structure of dispositional optimism:Ttraditional factor models and bifactor model.

Chinese Journal of Clinical Psychology,21

(1),45?47,105.[黎志華,尹霞云,蔡太生,朱翠英.(2013).特質樂觀的結構:傳統因素模型與雙因素模型.

中國臨床心理學雜志,21

(1),45?47,105.]Morgan,G.,Hodge,K.J.,Wells,K.E.,&Watkins,M.M.(2015).Are fit indices biased in favor of bi-factor models in cognitive ability research?:A comparison of fit in correlated factors,higher-order,and bi-factor models via monte carlo simulations.

Journal of Intelligence,3

(1),2?20.Mulaik,S.A.,&Quartetti,D.A.(1997).First order or higher order general factor?

Structural Equation Modeling:A Multidisciplinary Journal,4

(3),193?211.Musek,J.(2007).A general factor of personality:Evidence for the big one in the five-factor model.

Journal of Research in Personality,41

(6),1213?1233.Muthén,B.,Kaplan,D.,&Hollis,M.(1987).On structural equation modeling with data that are not missing completely at random.

Psychometrika,52

(3),431?462.Reise,S.P.(2012).The rediscovery of bifactor measurement models.

Multivariate Behavioral Research,47

(5),667?696.Reise,S.P.,Moore,T.M.,&Haviland,M.G.(2010).Bifactor models and rotations:Exploring the extent to which multidimensional data yield univocal scale scores.

Journal of Personality Assessment,92

(6),544?559.Reise,S.P.,Morizot,J.,&Hays,R.D.(2007).The role of the bifactor model in resolving dimensionality issues in health outcomes measures.

Quality of Life Research,16

(S1),19?31.Reise,S.P.,Scheines,R.,Widaman,K.F.,&Haviland,M.G.(2013).Multidimensionality and structural coefficient bias in structural equation modeling:A bifactor perspective.

Educational and Psychological Measurement,73

(1),5?26.Rindskopf,D.,&Rose,T.(1988).Some theory and applications of confirmatory second-order factor analysis.

Multivariate Behavioral Research,23

(1),51?67.Rodriguez,A.,Reise,S.P.,&Haviland,M.G.(2016).Evaluating bifactor models:Calculating and interpreting statistical indices.

Psychological Methods,21

(2),137?150.Schmid,J.,&Leiman,J.M.(1957).The development of hierarchical factor solutions.

Psychometrika,22

(1),53?61.Spearman,C.(1927).

The abilities of man:Their nature and measurement

.New York:MacMillan.Wang,D.F.,&Cui,H.(2005).

Explorations of Chinese personality

.Beijing,China:Social Sciences Academic Press.[王登峰,崔紅.(2005).

解讀中國人的人格

.北京:社會科學文獻出版社.]Watters,C.A.,Keefer,K.V.,Kloosterman,P.H.,Summerfeldt,L.J.,&Parker,J.D.A.(2013).Examining the structure of the internet addiction test in adolescents:A bifactor approach.

Computers in Human Behavior,29

(6),2294?2302.Yung,Y.-F.,Thissen,D.,&McLeod,L.D.(1999).On the relationship between the higher-order factor model and the hierarchical factor model.

Psychometrika,64

(2),113?128.