對一道求三角形內角平分線夾角題的探究

巨明杰+李紅紅

一、問題的提出

《義務教育數學課程標準》明確提出了學生要理解三角形角平分線的含義，探索并證明三角形、多邊形的內角和。筆者在現行華東師大版七年級數學下冊第九章“三角形”的教學中，發現教材、教輔無不涉及“已知三角形的一個內角，求另兩個內角角平分線夾角”的問題。

如圖1所示，在△ABC中，∠A=α，點O是∠ABC與∠ACB的平分線BF和CE的交點，求∠BOC.

解∵BF和CE分別是∠ABC與∠ACB的平分線，

∴∠OBC=∠ABC，∠OCB=∠ACB.

∴∠OBC+∠OCB=（∠ABC+∠ACB）=（180°-∠α）=90°-∠α.

∴∠BOC=180°-（∠OBC+∠OCB）=180°-（90°-∠α）=90°+∠α.

該題是在已知三角形一個內角的情況下，求出了另兩個內角平分線的夾角。我們逐步引導學生將求兩內角平分線的夾角改為一內一外角或兩外角角平分線的夾角；或將三角形改為多邊形的情況作了深入探究，發現了其中的規律，激發了學生的學習興趣，在教學中收到了較好的效果?，F介紹如下，僅供同仁們參考。

二、問題的探究

1.將內角平分線改為外角平分線

情形一：求三角形的一條內角平分線與一條外角平分線的夾角

如圖2，在△ABC中，∠A=α，點O是∠ABC與外角∠ACD的平分線BO和CO的交點，求∠BOC.

解∵BO和CO分別是∠ABC與∠ACD的平分線，

∴∠OBC=∠ABC，∠OCD=∠ACD.

∵2∠OCD=2∠OBC+∠α，

∴2（∠OCD-∠OBC）=∠α.

又∵∠BOC=∠OCD-∠OBC，即2∠BOC=∠α.

∴∠BOC=∠α.

情形二：求三角形的兩條外角平分線的夾角

如圖3，在△ABC中，∠A=α，點O是三角形兩外角∠DBC與∠ECB的平分線BO和CO的交點，求∠BOC.

解∵BO和CO分別是∠DBC與∠ECB的平分線，

∴∠OBC=∠DBC，∠OCB=∠ECB

∵2（∠OBC+∠OCB）=360°-（180°-∠α），

又∵∠BOC=180°-（∠OBC+∠OCB），

∴2（180°-∠BOC）=180°+∠α，

∴2∠BOC=180°-∠α.∴∠BOC=90°-∠α.

2.將三角形改為多邊形

（1）四邊形的情形

情形一：如圖4，在四邊形ABCD中，點O是兩內角∠ABC與∠DCB的平分線BO和CO的交點，證明：∠BOC=（∠A+∠D）.

證明∵BO和CO分別是∠ABC與∠DCB的角平分線，

∴∠OBC=∠ABC，∠OCB=∠DCB.

∴2（∠OBC+∠OCB）=360°-（∠A+∠D）.

∴2（180°-∠BOC）=360°-（∠A+∠D），

∴360°-2∠BOC=360°-（∠A+∠D），∴∠BOC=（∠A+∠D）

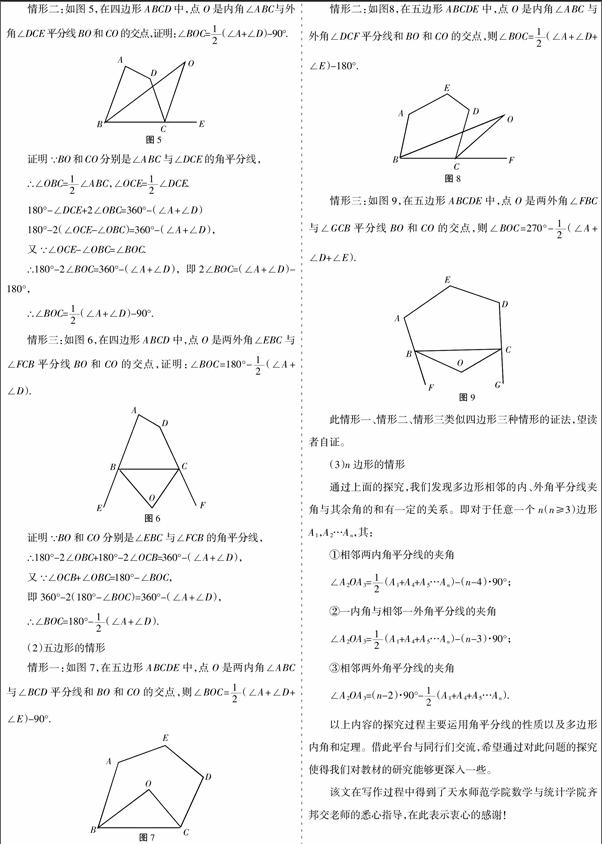
情形二：如圖5，在四邊形ABCD中，點O是內角∠ABC與外角∠DCE平分線BO和CO的交點，證明：∠BOC=（∠A+∠D）-90°.

證明∵BO和CO分別是∠ABC與∠DCE的角平分線，

∴∠OBC=∠ABC，∠OCE=∠DCE.

180°-∠DCE+2∠OBC=360°-（∠A+∠D）

180°-2（∠OCE-∠OBC）=360°-（∠A+∠D），

又∵∠OCE-∠OBC=∠BOC.

∴180°-2∠BOC=360°-（∠A+∠D），即2∠BOC=（∠A+∠D）-180°，

∴∠BOC=（∠A+∠D）-90°.

情形三：如圖6，在四邊形ABCD中，點O是兩外角∠EBC與∠FCB平分線BO和CO的交點，證明：∠BOC=180°-（∠A+∠D）.

證明∵BO和CO分別是∠EBC與∠FCB的角平分線，

∴180°-2∠OBC+180°-2∠OCB=360°-（∠A+∠D），

又∵∠OCB+∠OBC=180°-∠BOC，

即360°-2（180°-∠BOC）=360°-（∠A+∠D），

∴∠BOC=180°-（∠A+∠D）.

（2）五邊形的情形

情形一：如圖7，在五邊形ABCDE中，點O是兩內角∠ABC與∠BCD平分線和BO和CO的交點，則∠BOC=（∠A+∠D+∠E）-90°.

情形二：如圖8，在五邊形ABCDE中，點O是內角∠ABC與外角∠DCF平分線和BO和CO的交點，則∠BOC=（∠A+∠D+∠E）-180°.

情形三：如圖9，在五邊形ABCDE中，點O是兩外角∠FBC與∠GCB平分線BO和CO的交點，則∠BOC=270°-（∠A+∠D+∠E）.

此情形一、情形二、情形三類似四邊形三種情形的證法，望讀者自證。

（3）n邊形的情形

通過上面的探究，我們發現多邊形相鄰的內、外角平分線夾角與其余角的和有一定的關系。即對于任意一個n（n≥3）邊形A1，A2…An，其：

①相鄰兩內角平分線的夾角

∠A2OA3=（A1+A4+A5…An）-（n-4）·90°；

②一內角與相鄰一外角平分線的夾角

∠A2OA3=（A1+A4+A5…An）-（n-3）·90°；

③相鄰兩外角平分線的夾角

∠A2OA3=（n-2）·90°-（A1+A4+A5…An）.

以上內容的探究過程主要運用角平分線的性質以及多邊形內角和定理。借此平臺與同行們交流，希望通過對此問題的探究使得我們對教材的研究能夠更深入一些。

該文在寫作過程中得到了天水師范學院數學與統計學院齊邦交老師的悉心指導，在此表示衷心的感謝！