典型放電氣體的擊穿場強閾值研究

李志剛， 程 立， 汪家春， 王啟超， 時家明

(脈沖功率激光技術國家重點實驗室， 安徽 合肥 230037)

?

典型放電氣體的擊穿場強閾值研究

李志剛*， 程 立， 汪家春， 王啟超， 時家明

(脈沖功率激光技術國家重點實驗室， 安徽 合肥 230037)

為了研究等離子體產生時的氣體擊穿特性，利用低氣壓條件下氣體擊穿場強閾值模型，分析了He、Ne、Ar、Kr、Xe和Hg蒸汽等6種典型放電氣體的擊穿閾值隨入射波頻率、電子溫度、氣體壓強以及氣體溫度的變化規律。結果表明：氣體擊穿閾值隨氣體壓強的增大而減小，隨氣體溫度、電子溫度和入射脈沖頻率的增大而增大。氣體壓強和入射頻率對擊穿閾值的影響大于氣體溫度和電子溫度，在所考慮的范圍內，氣體壓強對擊穿場強的影響約為100 V/m，入射脈沖頻率對擊穿場強的影響為50～300 V/m，氣體溫度和電子溫度對擊穿場強的影響為20～30 V/m。當考慮氣體壓強、氣體溫度以及電子溫度等因素的影響時，各種氣體的擊穿場強閾值產生的變化規律相類似；但考慮入射頻率的影響時，不同氣體的擊穿場強閾值差異很大。在所考慮的典型放電氣體中，Xe具有最低的擊穿場強閾值，He的擊穿閾值最大。

氣體擊穿； 擊穿閾值； 等離子體； 電磁脈沖防護

1 引 言

在伊拉克戰爭中，美軍使用電磁脈沖炸彈攻擊伊拉克國家電視臺，迫使電視臺及其周邊區域電力、通信、交通等設施中斷數小時，造成了巨大破壞[1]。電磁脈沖武器的強大威力使其在未來戰爭中必將發揮極其重要的作用，然而，目前還沒有有效途徑能夠很好地進行防御。因此，世界各國紛紛開發新型防護材料來防護其攻擊。等離子體作為一種新型防護材料而備受關注，科技人員已開展了大量的研究工作。

Krlin等研究了高幅值雜波與等離子體相互作用產生的非線性效應，并分析了這種效應對等離子體中的電子密度分布產生的影響[2]。Bonaventura等對于高功率微波脈沖導致的N2等離子體參數變化進行了系統研究[3-5]。Kikel等提出了等離子體限幅器的概念，并認為其可以用于電磁脈沖武器的防護[6]。周前紅等研究分析了110 GHz微波電離大氣產生的等離子體的過程，對不同氣壓條件下等離子體的產生狀態進行了細致描述[7]。楊一明等實驗研究了空氣和SF6氣體擊穿對微波傳輸的影響，結果表明擊穿產生的等離子體會對射微波產生較大的衰減[8]。舒楠等提出在屏蔽腔中引入等離子體，構造了等離子體的雙層屏蔽腔模型，用以提高屏蔽腔對電磁脈沖的屏蔽效能[9]。袁忠才等設計了等離子體-吸波材料-等離子體夾層結構，用來進行強電磁脈沖防護[10]。程立等提出用于電磁脈沖防護的柱狀等離子體陣列結構，該結構可對入射電磁脈沖產生較強的衰減[11]。

等離子體的產生性能與發生單元填充的放電氣體密切相關，填充氣體發生擊穿現象是等離子體用于電磁防護的先決條件[12]。然而，目前對等離子體產生氣體的擊穿特性研究的報道相對較少，因此，本文針對6種典型放電氣體的擊穿場強閾值進行了分析，并研究了不同參數對擊穿閾值的影響效果。研究結論對于等離子體產生氣體的選擇具有重要的指導意義。

2 氣體擊穿場強閾值模型

工程上，通常采用氣體放電方式產生等離子體。等離子體發生管中往往填充一種或者幾種放電氣體，填充氣體決定了等離子體的性能。當電磁脈沖在填充氣體中傳播時，所包含的電場和磁場分量會對氣體中中性原子或分子產生加速電離作用，改變填充氣體中的電子數密度[13]。當入射電磁脈沖能量密度較小時，電磁脈沖激勵的電場強度不足以使填充氣體進一步電離，此時，填充氣體處于弱電離狀態，即氣體電離產生自由電子的速率小于自由電子通過復合、吸附、擴散作用而消失的速率；當入射電磁脈沖的能量密度足夠大時，填充氣體中的自由電子會對激勵的電場強度做出很強的響應，氣體電子產生的速度大大超過消失速度，電子數濃度呈指數增加，此時，填充氣體中電離現象加劇，發生類似于擊穿的效果。

因此，當電場強度超過一定值時，氣體電離產生電子的速率將會超過電子因復合、附著、擴散消失的速率，從而使得弱電離氣體中的電離度增大。處于臨界狀態時，電子產生的速率和消失的速率相等，此時，對應的電磁脈沖電場強度為擊穿電場強度閾值。電離過程可用電離動態方程描述：

vi(Et)=vr(Et)+va(Et)+vd,

(1)

其中，Et是擊穿電場強度閾值，vi是電離速率，vr是復合速率，va是附著速率，vd是擴散速率。

通過求解式(1)可以得到擊穿電場強度閾值。在低氣壓下，氣體中的電磁脈沖電離場強閾值為：

(2)

其中，νm為氣體電子與中性粒子的碰撞頻率，可表示為：

(3)

將式(3)帶入式(2)，得到

(4)

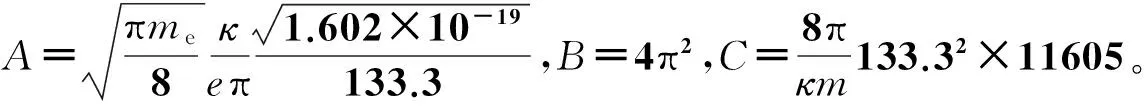
(5)

其中，κ為玻耳茲曼常數，κ=1.38×10-23J/K；e為電子電荷，e=1.602×10-19C；me為電荷質量，me=9.109×10-31kg；σm為碰撞截面，σm=πr2；r為填充氣體的粒子碰撞半徑；φi為中性粒子的電離勢能，單位為eV；p為氣體壓強，單位為Torr(1 Torr =133.3 Pa)；ω為入射脈沖角頻率；T為氣體溫度，單位為K；Te為電子溫度，單位為eV(1 eV=11 605 K)；Λ是特征擴散長度，與裝載氣體的容器尺寸有關。

對于特定的容器、特定的氣體和入射電磁脈沖，可以通過式(5)得到其電離閾值場強。

3 不同參數對擊穿場強閾值的影響

通過對式(5)進行分析，可以得出氣體擊穿場強閾值與入射電磁脈沖頻率、電子與中性粒子的碰撞半徑和電子溫度、填充氣體的氣壓、溫度以及電離勢能有關。本文選取幾種典型的放電氣體計算分析其變化規律。

3.1放電氣體的選擇

在分析過程中，本文選擇了He、Ne、Ar、Kr、Xe和Hg蒸汽6種典型放電氣體作為研究對象，這6種氣體可用作等離子體的產生。6種氣體的氣體碰撞半徑和電離能如表1所示。

表1 典型的放電氣體或者蒸汽的碰撞半徑和電離能

Tab.1 Collision radius and ionization energy of common charge gases or vapor

氣體種類碰撞半徑r/(10-10m)電離能Φi/eVHe1.0924.58Ne1.2921.55Ar1.8215.75Kr2.0813.96Xe2.4312.12Hg1.5810.43

另外，本文選擇圓柱形放電單元作為氣體容器，如圖1所示。圓柱形管半徑為2.5 cm，長度為60 cm。

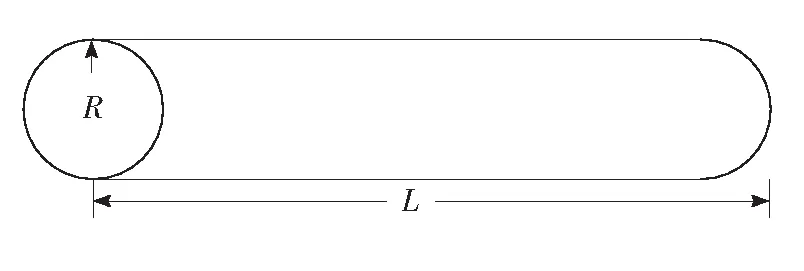
圖1 圓柱容器示意圖

對于圓柱形容器來說，特征擴散長度Λ可以表示為：

(6)

其中，R是圓柱容器半徑，L是圓柱容器長度。

3.2填充氣壓對擊穿場強閾值的影響

圖2給出了所選氣體的擊穿場強閾值與填充氣壓的變化關系，圖中橫、縱坐標均為對數坐標。容器內氣體溫度為300 K，電子溫度為0.05 eV，入射波頻率為1 GHz。從圖中可以看出，在所考察的范圍內，隨著氣壓的升高，不同氣體的擊穿場強閾值均有減小的趨勢，且Xe一直具有最低的電離閾值，而Kr、Ar、Hg蒸汽、Ne、He的擊穿場強閾值則依次增大。另外，從圖2中還可以分析得到，氣體壓強對擊穿場強閾值的影響較大，尤其在氣壓較小時。總體來說，氣壓變化666 Pa(5 Torr)，場強閾值變化兩個數量級。以Ar氣體為例，當氣體壓強由0 提高到133.3 Pa(1 Torr)時，擊穿場強閾值由100 V/cm衰減為10 V/cm；當氣體壓強由133.3 Pa(1 Torr)升高到666 Pa(5 Torr)時，擊穿場強閾值由10 V/cm減小為2 V/cm左右。其他氣體與之相類似，場強閾值變化在兩個數量級上。在氣壓大于133.3 Pa(1 Torr)時，Hg蒸汽、Ar、Kr、Xe均具有低至10 V/cm以下的擊穿場強閾值，其中Hg蒸汽、Ar具有非常接近的擊穿閾值。

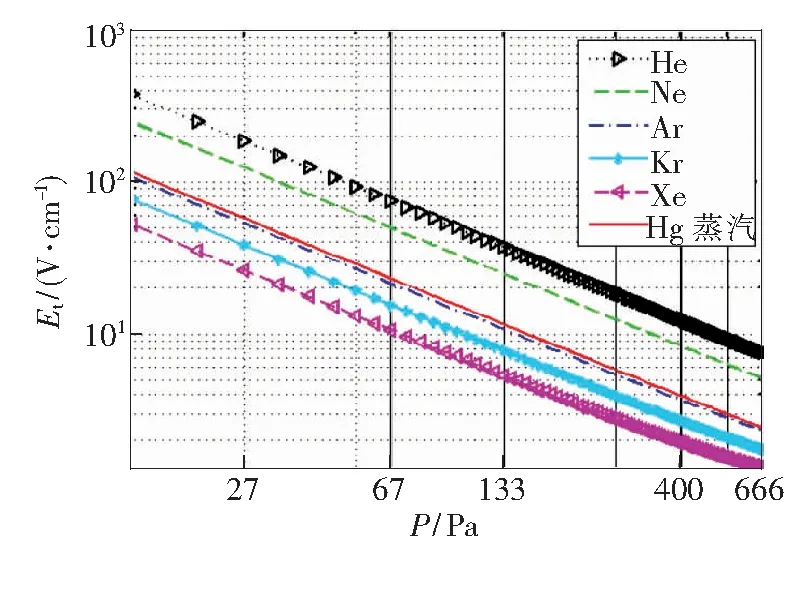
圖2 氣體壓強對擊穿場強閾值的影響

3.3填充氣體溫度對擊穿場強閾值的影響

圖3反映了不同氣體擊穿場強閾值與填充氣體溫度的變化關系，圖中橫、縱坐標均為對數坐標。容器內填充氣壓為133.3 Pa(1 Torr)，電子溫度為0.05 eV，入射波頻率為1 GHz。從圖中可以看出，隨著氣體溫度的升高，不同氣體的擊穿場強閾值均有增大的趨勢，其中Hg蒸汽、Ar具有非常接近的擊穿閾值。另外，從圖3中通過分析可以得到，氣體溫度對氣體擊穿場強閾值的影響在一個數量級左右，當氣體溫度由300 K上升到1 300 K時，擊穿場強閾值大約改變30 V/cm；同時，隨著氣體溫度的變化，擊穿閾值的改變幅值較為均勻。同樣以Ar氣體為例，當氣體溫度由300 K上升到600 K時，擊穿閾值提高了約10 V/cm；當溫度由600 K上升到900 K時，閾值同樣提高了10 V/cm；當溫度由900 K上升到1 300 K時，擊穿閾值也提高了約10 V/cm。其他氣體也有類似規律。值得注意的是，Xe在300～600 K較大的溫度范圍內一直具有10 V/cm以下的擊穿場強閾值。

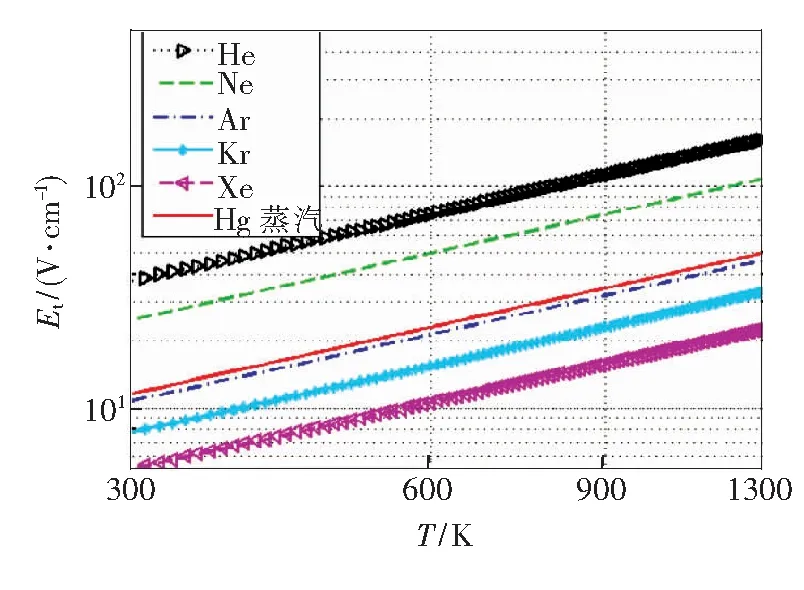
圖3 氣體溫度對擊穿場強閾值的影響

3.4電子溫度對擊穿場強閾值的影響

圖4反映了不同氣體擊穿場強閾值與電子溫度的變化關系。容器內填充氣壓為133.3 Pa(1 Torr)，氣體溫度為300 K，入射波頻率為1 GHz。從圖中可以看出，隨著電子溫度的升高，不同氣體的擊穿場強閾值均有增大的趨勢，Xe依然具有所列氣體中最低的擊穿閾值。分析圖中變化曲線可以得到，電子溫度對擊穿場強閾值的影響不是很大。電子溫度變化50 eV時，場強閾值僅僅變化了20 V/m左右。同樣以Ar舉例說明，當電子溫度由0上升到50 eV時，擊穿場強閾值由10 V/m增大到30 V/m，其他氣體也有相類似的變化規律。

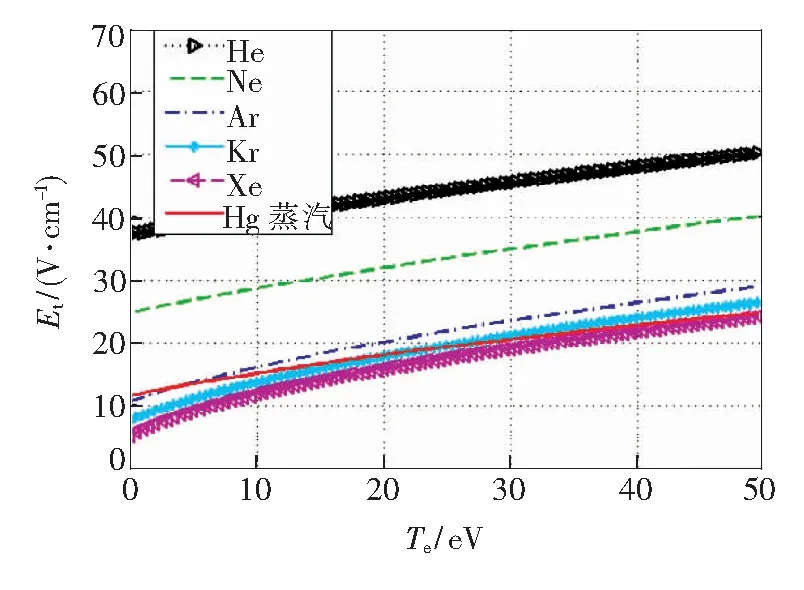
圖4 電子溫度對擊穿場強閾值的影響Fig.4 Effects of electron temperature on breakdown threshold

3.5入射波頻率對擊穿場強閾值的影響

圖5反映了不同氣體擊穿場強閾值與入射波頻率的變化關系。容器內填充氣壓為133.3 Pa(1 Torr)，氣體溫度為300 K，電子溫度為0.05 eV，入射波頻率為1 GHz。從圖中可以看出，隨著入射波頻率的增大，不同氣體的擊穿場強閾值均有增大的趨勢。另外，入射頻率對不同氣體的擊穿閾值的響應不同，對He的影響最大，擊穿場強閾值增大得最快，入射頻率變化10 GHz，擊穿閾值增加300 V/m左右。其次是Ne，Ar、Kr、Xe和Hg蒸汽的變化幅值相近，約在50～100 V/m。Xe具有所列氣體中最低的擊穿閾值。

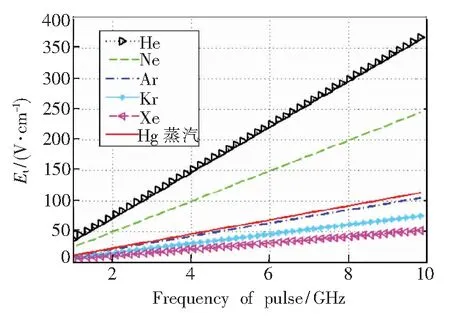
圖5 入射波頻率對擊穿場強閾值的影響

Fig.5 Effects of incident frequency on breakdown threshold

4 結果分析

通過上述分析，可以看出氣體擊穿場強閾值會隨著入射電磁脈沖頻率、電子溫度、填充氣體的氣壓、溫度以及電離勢能等因素的變化而改變，基本規律可以歸結為以下幾個方面：

(1)氣體擊穿場強閾值隨氣體壓強的增大而減小。當氣壓很低時，填充氣體中的中性粒子密度很低，電子碰撞中性粒子并使其產生電離的機率較小。這樣，為了使氣體產生擊穿，所需的電場強度也就很大。當氣壓升高時，氣體的中性粒子的密度也隨之升高，其被電離的機率也就變大，擊穿電場強度閾值也將變小。

(2)氣體擊穿場強閾值隨氣體溫度和電子溫度的升高而增大。氣體溫度和電子溫度的升高會導致氣體粒子的無規則運動加劇，從而使得填充氣體中擴散作用增大，電子消失的速率隨之增大，填充氣體發生電離的概率相對較小。為達到氣體擊穿的程度，需要增大外加電場強度，減小電子的擴散作用，增大中性粒子被電離的概率。因此，隨著氣體溫度和電子溫度的升高，氣體擊穿場強閾值增大。

(3)氣體擊穿場強閾值隨入射脈沖頻率的增大而增大。由于電場存在正向和反向幅值，當入射波頻率較大時，電子在電場中尚未被加速到足以電離中性粒子的程度就已經被反向電場減速，中性粒子每次通過碰撞獲得電離的能量較小。為使填充氣體產生擊穿效應，需要提高外加電場強度，因此，隨著入射脈沖頻率的增大，氣體擊穿場強閾值增大。

(4)對于影響氣體擊穿場強閾值的各項因素，氣體壓強和入射頻率的影響大于氣體溫度和電子溫度。在所考慮的范圍內，氣體壓強對擊穿閾值的影響大約為100 V/m，入射脈沖頻率的影響為50～300 V/m，氣體溫度和電子溫度的影響為20～30 V/m。另外，對于氣體壓強、氣體溫度以及電子溫度等影響，各種氣體的擊穿場強閾值產生的變化規律相類似；但對于入射脈沖頻率的影響，不同氣體的擊穿閾值差異很大。

(5)本文研究的是低氣壓情形下的氣體擊穿場強閾值的變化規律，在高氣壓條件下將不再適用。在低氣壓條件下，擴散作用在電子消失的影響因素中占主導地位，本文在進行研究時主要考慮了電子的擴散作用；而在高氣壓條件下，電子的擴散作用減弱，計算公式(2)～(5)已不再適用，氣體擊穿場強閾值的變化規律需要重新考慮。

5 結 論

本文主要開展了低氣壓條件下常見放電氣體的擊穿場強閾值研究，計算分析了入射脈沖頻率、電子溫度、氣體壓強以及氣體溫度等因素對擊穿場強閾值的影響。結果表明，氣體擊穿場強閾值隨填充氣體壓強的增大而減小，隨氣體溫度、電子溫度和入射脈沖頻率的增大而增大。氣體壓強和入射頻率的影響大于氣體溫度和電子溫度的影響。在所考慮的范圍內，氣體壓強對擊穿場強的影響大約為100 V/m，入射脈沖頻率的影響在50～300 V/m，氣體溫度和電子溫度的影響大約為20～30 V/m。對于氣體壓強、氣體溫度以及電子溫度等因素的影響，各種氣體的擊穿場強閾值產生的變化規律相類似；但對于入射脈沖頻率的影響，不同氣體的擊穿閾值差異很大。在所考慮的常見放電氣體中，Xe具有最低的擊穿場強閾值，He的擊穿閾值最大。利用等離子體進行電磁脈沖防護時，需要合理選擇放電氣體填充到等離子體發生單元中。本文研究結論對于放電氣體的選擇具有重要的指導意義。

[1] 余世里. 高功率微波武器效應及防護 [J]. 微波學報, 2014, 30(S2):147-151. YU S L. High power microwave weapons effect and hardening [J].J.Microw., 2014, 30(S2):147-151. (in Chinese)

[2] KRLíN L, PAVLO P, PNEK R,etal.. Nonlinear effects in LH wave-plasma interaction [J].PlasmaPhys.ControlledFusion, 2002, 44(2):159-170.

[3] BONAVENTURA Z, TRUNEC D, MEKO M,etal.. Theoretical study of pulsed microwave discharge in nitrogen [J].PlasmaSourcesSci.Technol., 2005, 14(4):751-756.

[4] BONAVENTURA Z, TRUNEC D, MEKO M,etal.. Self-consistent spatio-temporal simulation of pulsed microwave discharge [J].J.Phys. D:Appl.Phys., 2008, 41(1):015210.

[6] KIKEL A, ALTGILBERS L, MERRITT I,etal.. Plasma limiters, AIAA-98-2564 [R]. AIAA-98-2564, 1998.

[7] 周前紅, 董志偉, 陳京元. 110 GHz微波電離大氣產生等離子體過程的理論研究 [J]. 物理學報, 2011, 60(12):125202-1-12. ZHOU Q H, DONG Z W, CHEN J Y. Modeling of plasma pattern formation in 110 GHz microwave air breakdown [J].ActaPhys.Sinica, 2011, 60(12):125202-1-12. (in Chinese)

[8] 楊一明, 袁成衛, 錢寶良. 空氣和SF6氣體擊穿對微波傳輸的影響 [J]. 強激光與粒子束, 2012, 24(1):142-146. YANG Y M, YUAN C W, QIAN B L. Effect of air and SF6breakdown on transmission of high power microwave [J].HighPowerLaserPart.Beams, 2012, 24(1):142-146. (in Chinese)

[9] 舒楠, 張厚, 李圭源. 等,離子體在強電磁脈沖防護中的應用 [J]. 無線電工程, 2010, 40(10):55-57. SU N, ZHANG H, LI G Y. Research on application of plasma in EMP protection [J].RadioEng., 2010, 40(10):55-57. (in Chinese)

[10] YUAN Z C, SHI J M. Research on EM pulse protection property of plasma-microwave absorptive material-plasma sandwich structure [J].SciChinaTechnol.Sci., 2010, 53(12):3221-3224.

[11] 程立, 時家明, 汪家春, 等. 單層柱狀等離子體陣列對微波透射衰減影響的實驗研究 [J]. 真空科學與技術學報, 2014, 34(12):183-185. CHENG L, SHI J M, WANG J C,etal.. Influence of one-layer cylindrical plasma array on microwave transmission attenuation [J].Chin.J.Vac.Sci.Technol., 2014, 34(12):183-185. (in Chinese)

[12] 宋瑋, 邵浩, 張治強, 等. 射頻擊穿等離子體對高功率微波傳輸特性的影響 [J]. 物理學報, 2014, 63(6):064101-1-5. SONG W, SHAO H, ZHANG Z Q,etal.. High power microwave propagation properties in radio frequency breakdown plasma [J].ActaPhys.Sinica, 2014, 63(6):064101-1-5. (in Chinese)

[13] 鄭靈, 趙青, 羅先剛, 等. 等離子體中電磁波傳輸特性理論與實驗研究 [J]. 物理學報, 2012, 61(15):155203-1-7. ZHENG L, ZHAO Q, LUO X G,etal.. Theoretical and experimental studies of electromagnetic wave transmission in plasma [J].ActaPhys.Sinica, 2012, 61(15):155203-1-7. (in Chinese)

李志剛(1990-)，男，山東濟寧人，博士研究生，2015年于電子工程學院獲得碩士學位，主要從事光電隱身與等離子體防護方面的研究。

E-mail: class1_48@163.com

Field Strength Threshold of Common Discharge Gases Breakdown

LI Zhi-gang*, CHENG Li, WANG Jia-chun, WANG Qi-chao, SHI Jia-ming

(StateKeyLaboratoryofPulsedPowerLaserTechnology,Hefei230037,China)
*CorrespondingAuthor,E-mail:class1_48@163.com

In order to study the properties of gas breakdown while plasma occurs, the threshold value was calculated according to the model of field strength threshold under the lower atmospheric pressure. Six kinds of common discharge gases including helium, neon, argon, krypton, xenon, and mercury vapor were taken into account. Moreover, the related change rule was analyzed and described with the incident frequency, electron temperature, gas pressure, and gas temperature considered. The results show that the gas breakdown threshold is affected by the four factors mentioned above. On the one hand, it decreases while the gas pressure increases. On the other hand, it increases with the gas temperature, electron temperature, and incident frequency increasing. The effects of the gas pressure and incident frequency play more of a role than that of gas temperature and electron temperature. The value of breakdown threshold changes about 100 V/m due to the influence of gas pressure. Similarly, it changes 50 V/m to 300 V/m, and 20 V/m to 30 V/m with the effects of incident frequency and gas or electron temperature thought about. What’s more, the change rule is found to be similar for all kinds of charge gases when the effects of gas pressure, gas temperature, and electron temperature are thought over. But it varies while the incident frequency is considered. In addition, xenon has the smallest threshold value while helium having the largest one among the gases studied.

gas breakdown; breakdown threshold; plasma; EMP defense

2016-07-06；

2016-08-17

國家高技術研究發展計劃(863)(2015AA0392)資助項目 Supported by National High Technology Research and Development Program(863)(2015AA0392)

1000-7032(2017)01-0103-06

O539； O461.2+5

A

10.3788/fgxb20173801.0103