海況干擾下潛艇六自由度運動分析

李慧, 趙琳, 毛英

(哈爾濱工程大學 自動化學院，黑龍江 哈爾濱 150001)

海況干擾下潛艇六自由度運動分析

李慧, 趙琳, 毛英

(哈爾濱工程大學 自動化學院，黑龍江 哈爾濱 150001)

為了彌補實際海試條件的局限性，輔助實現陸上鑒定敏感潛艇運動的導航系統設備的性能，本文對潛艇六自由度運動規律進行了研究，包括靜水以及海洋環境干擾下潛艇的直航和回轉運動。通過分析潛艇運動時所受的力及力矩，以及海浪、海流的基本模型，建立海洋環境干擾下的潛艇六自由度運動方程。針對潛艇的線運動、角運動相關信息，結合已有的經過實際試驗修正的某潛艇的部分水動力系數，對其直航、回轉運動進行了研究分析，仿真結果能夠較為真實地反應潛艇在海洋環境干擾下的運動情況，滿足實際工程中輔助測試的需求。

潛艇；運動模型；六自由度；海洋環境；海浪干擾；海流干擾

對于敏感潛艇運動的導航系統而言，在裝備前要對其進行性能鑒定，需要盡可能地遍歷潛艇出海時的各種運動，包括各種海洋環境干擾。實艇試驗成本高、風險大[1]，而且由于復雜海況的不可預見性，造成潛艇的短周期運動具有不可控性，海況(尤其是復雜海況)干擾造成的潛艇受迫運動無法實現人為控制，無法全面考察設備性能。這使得全面分析潛艇在海洋環境干擾下的六自由度運動十分有意義。利用陸地上建立的真實的潛艇模擬仿真環境，一定程度上彌補實際海試時條件的局限性，是一種很好的解決辦法。

本文研究了海況干擾下的潛艇運動，首先介紹了描述潛艇運動時所用到的坐標系，然后以格特勒的潛艇標準運動方程為基礎，進行適當簡化，結合海洋環境干擾模型，建立海況干擾下的潛艇六自由度運動方程。以某潛艇為研究對象，進行靜水和海況干擾下的直航、回轉運動仿真分析，最后得出潛艇六自由度運動的速度和姿態的變化特點。

1 坐標系

描述潛艇六自由度運動時采用了固定坐標系(或稱地面坐標系)及運動坐標系(或稱艇體坐標系)，按研究慣例，一律采用右手坐標系，參數、符號體系與國際水池會議(ITTC)及造船和輪機工程學會(SNAME)術語公報推薦的一致[2]。

固定坐標系的原點E可以任意選取海面或海中的某一點，本文將t=0時刻潛艇重心所在位置定為坐標原點，Eξ軸沿水平方向，以潛艇的主航向作為正向，Eη軸位于Eξ軸所在的水平面，且由Eξ軸順時針旋轉90°得到，Eζ軸垂直于Eη軸和Eξ軸構成的平面，其正向符合右手定則。

運動坐標系的坐標原點O通常選取在艇體的重心G處，Ox軸位于艇體縱中剖面內，沿水平線指向船艏方向為正，Oy軸與縱中剖面垂直，以指向右舷方向為正，Oz軸垂直于Ox軸與Oy軸所在的平面，以指向船底方向為正，固定坐標系及運動坐標系如圖1所示。

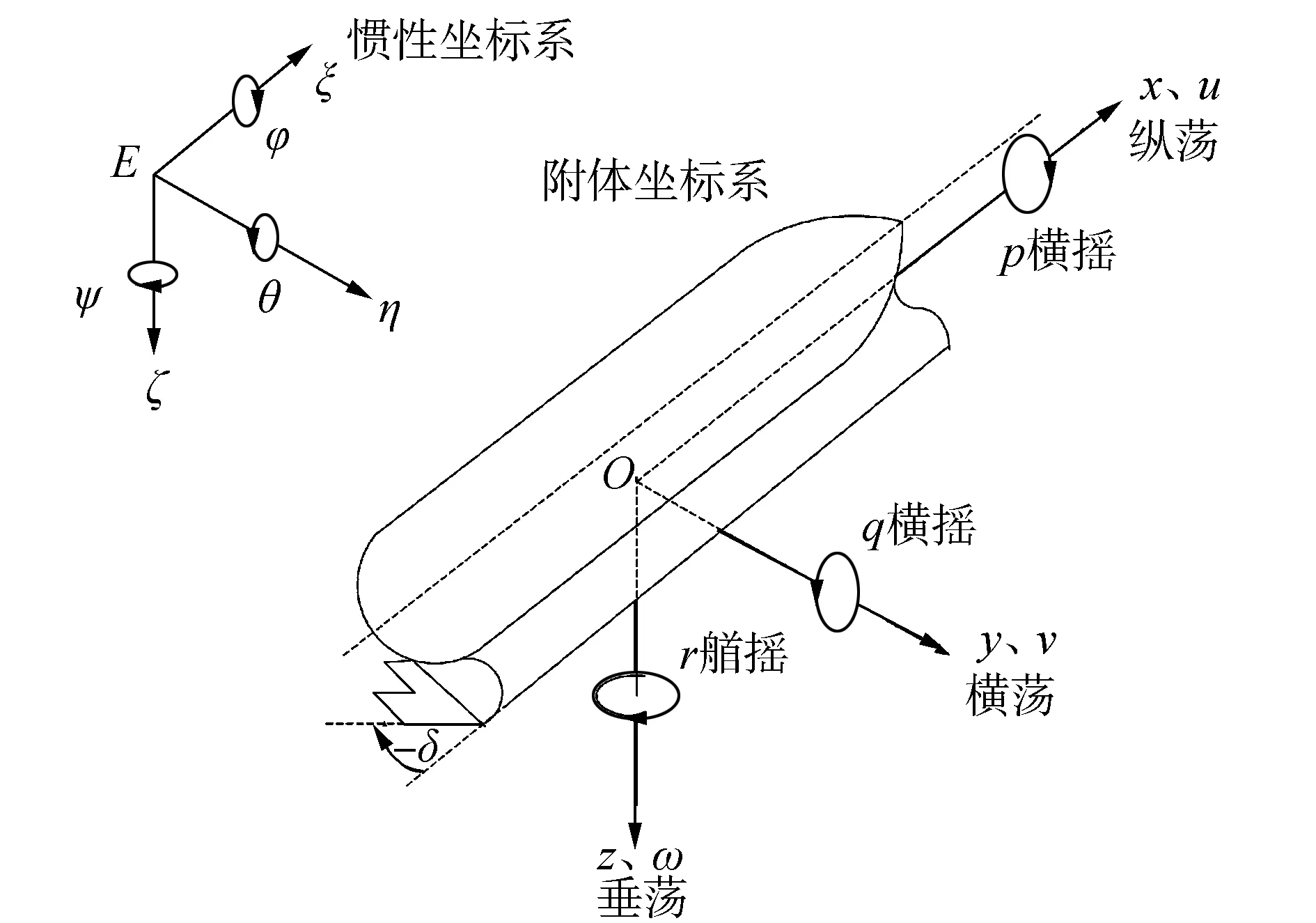
圖1 固定坐標系及運動坐標系Fig.1 Fixed coordinate system and moving coordinate system

設兩個坐標系原點重合，則固定坐標系可以通過三次正交旋轉與動系完全重合。表1中列出了本文在描述潛艇運動時常用參量的符號表示。

表1 運動坐標系的各參量符號

2 潛艇空間運動模型

2.1 潛艇六自由度運動模型

潛艇六自由度空間運動方程[3-4]以1967年泰勒海軍潛艇研究和發展中心發表的格特勒《用于潛艇模擬研究的標準運動方程》為基礎，該方程含108個水動力系數，實際中由于試驗的困難很難全部得到，在不影響潛艇六自由度運動的主要特性下，可對標準方程進行簡化處理，假設條件主要有[5-6]：1)潛艇左右對稱；2)潛艇重心與原點重合；3)潛艇運動狀態對舵力沒有影響，且不考慮舵之間的相互耦合；4)忽略對潛艇運動影響非常小的二階水動力系數及其耦合系數；5)忽略潛艇垂直面的速度對水平面的運動耦合。

根據以上簡化條件，得到簡化后的潛艇六自由度運動力與力矩的方程如式(1)～(6)，其中前三個方程為力的方程，后三個方程為力矩方程。

軸向力方程：

(1)

橫向力方程：

(2)

垂向力方程：

(3)

橫傾力矩方程：

(4)

縱傾力矩方程：

(5)

偏航力矩方程：

(6)

結合潛艇六自由度運動輔助方程為[7]

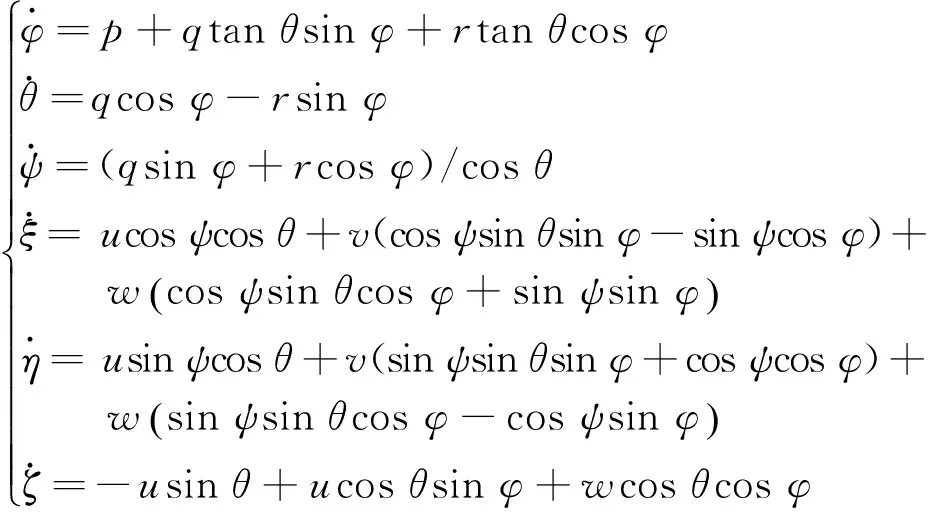
(7)

若已知潛艇水動力系數，對于任何操縱信息(包括舵、槳等)，采用四階龍格-庫塔積分算法對潛艇六自由度運動模型進行求解，可快速得到艦潛艇動狀態的數值解，包括潛艇的三維速度、角速度、姿態及軌跡。

2.2 海洋環境干擾模型

潛艇的戰術任務主要是在近水面完成的，如水深十多米處發射導彈等，不可避免地受到海浪和海流的影響而產生搖蕩[8]，為了更真實的模擬潛艇在海洋中的運動狀況，本文對海浪和海流干擾下的潛艇運動進行了仿真研究。

2.2.1 作用在潛艇上的海浪干擾模型

為了提高仿真模型的精度，同時滿足實時仿真的需求，本文采用十二屆ITTC提供的雙參數隨機海浪頻譜來實時仿真長峰波隨機海浪。

ITTC提供的雙參數海浪譜為[9]

(8)

根據能量等效原則，遭遇頻率能量譜密度函數與自然頻率能量密度函數之間的關系為

(9)

式中：V為潛艇航速，β為浪向角，g為重力加速度。

潛艇在海浪作用下所受到力及力矩可主要考慮為橫搖力矩，縱搖力矩及垂向作用力，其受力模型分別介紹如下：

1)潛艇受海浪作用橫搖力矩

作用于潛艇上的海浪橫搖力矩[10]：

(10)

海浪作用下潛艇橫搖的波傾角仿真模型為

式中：n為諧波個數，ωi為第i個海浪諧波的頻率，Δω為頻率增量，Sα(ωi)為第i個諧波波傾角能量譜密度。

2)潛艇受海浪作用縱搖力矩

作用于潛艇上的海浪縱搖力矩[10]：

(12)

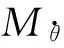
本文中所用到的海浪作用下的潛艇縱搖的波傾角仿真模型為

(13)

3)潛艇垂向受海浪的作用力

本文采用Hirom近似公式來計算作用于潛艇垂向上的海浪一階垂蕩力[11]，當潛艇深度變化值和縱搖角都較小的情況下，潛艇在近水面所受的波浪力為

(14)

2.2.2 作用在潛艇上的海流干擾模型

海流的處理，采用均勻定常流的假設，對于非高速運動的潛艇，只是從運動學上考慮其對潛艇的影響。若VC為流速，ψC為流向，則流速VC在附體坐標軸上的分量為

(15)

潛艇運動對水流的相對速度的投影ur、vr：

(16)

將海浪模型中的力和力矩加入到潛艇六自由度運動方程，引入海浪干擾信息，而對于海流，由于只考慮運動學上的影響，故按上式進行處理。

3 某潛艇六自由度運動仿真試驗

水下回轉是潛艇轉向運動的重要研究內容[12]，本文根據上小節中建立的潛艇六自由度運動模型及海洋環境干擾模型，以某潛艇為仿真對象，給出了該潛艇在靜水中、海洋環境干擾下的直航及回轉運動情況。

3.1 靜水中潛艇回轉

靜水中潛艇直航相對較簡單，本文僅給出靜水中回轉運動的仿真，設定初始航速20 kn，航向角為0°，即正北向航行，調整螺旋槳推力以固定航速，方向舵角分別給為10°、20°、30°，艏艉升降舵角為0，即不進行定深控制。

(a)運動軌跡

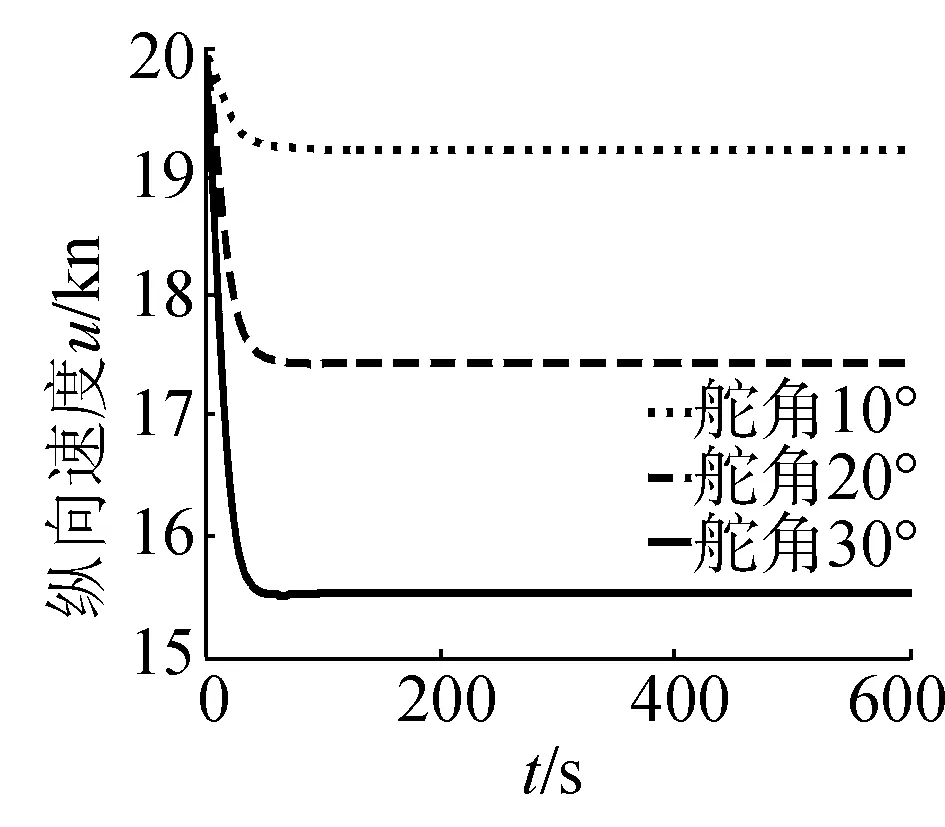
(b)縱向速度曲線

(c)橫搖角速率曲線

(d)橫搖角曲線

(e)縱搖角速率曲線

(f)縱搖角曲線

(g)艏搖角速率曲線

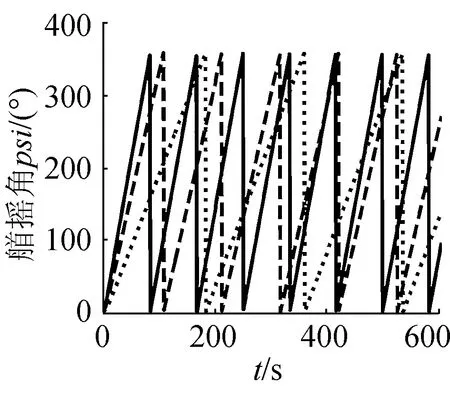
(h)艏搖角曲線

圖2為該潛艇在靜水中固定航速改變方向舵角進行的回轉運動，圖中列出了某潛艇的軌跡、軸向速率、三維角速率以及三維姿態角圖。由圖中可以看出，潛艇方向舵角由10°、20°、30°依次增大時，潛艇在回轉過程中的漂角也相應增大，其回轉圈的半徑越小；潛艇縱向阻力依次增大，其速降越嚴重；潛艇定常回轉時的向心力也依次增大，其橫向力應等于向心力在橫向的投影，橫向力對重心的力矩與扶正力矩平衡，潛艇定常回轉時的橫傾角也相應的增大。

如果方向舵角固定為20°，調節螺旋槳推力使潛艇的速度分別固定在9、15、20 kn，其運動狀態如圖3。

(a)運動軌跡

(b)縱向速度曲線

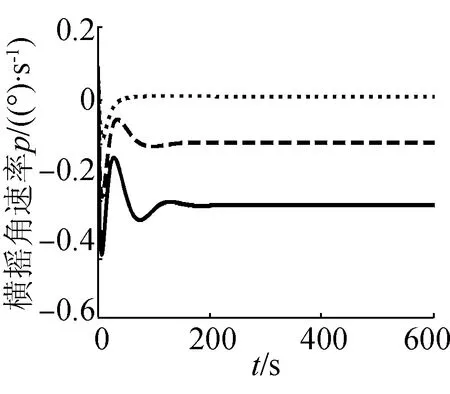
(c)橫搖角速率曲線

(d)橫搖角曲線

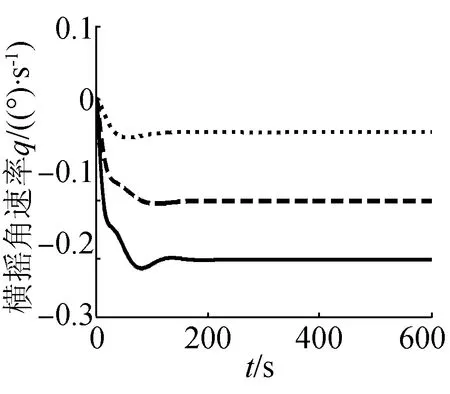
(e)縱搖角速率曲線

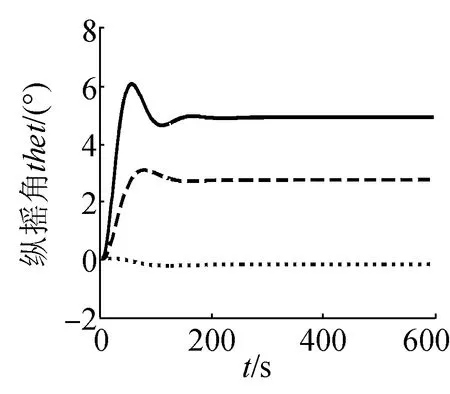
(f)縱搖角曲線

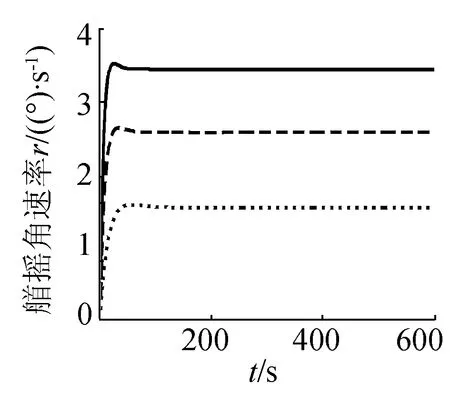
(g)艏搖角速率曲線

(h)艏搖角曲線

圖3為潛艇在靜水中固定舵角改變航速進行的回轉運動，從三種速度下的航跡圖可以看出，航速對潛艇定常回轉直徑的影響不大；潛艇定常回轉時其橫傾角與航速的平方存在正比關系，因而隨著航速增大，橫傾角也相應增大，穩態時的橫傾角也越大，當航速為20 kn時，穩定橫傾角達3.8°。縱傾角也隨著航速的增大而增大，當航速為20 kn時，穩定縱傾角達到5°。

3.2 海浪對潛艇運動的干擾作用

海浪的大小決定了海面的粗糙程度，進一步影響了潛艇的運動，本節在靜水的基礎上加上海浪干擾對潛艇運動影響進行仿真。設潛艇航速20 kn，航向角為0°，即正北向航行，初始深度為5 m，方向舵角為0°，首尾升降舵角為0°，不進行定深控制。按實際海域統計得到的海浪參數對仿真模型進行修正，其中海浪浪高為1.28 m，浪向角為30°，潛艇的軌跡及橫搖和縱搖曲線如圖4所示。

(a)運動軌跡

(b)縱向速度曲線

(c)橫搖角速率曲線

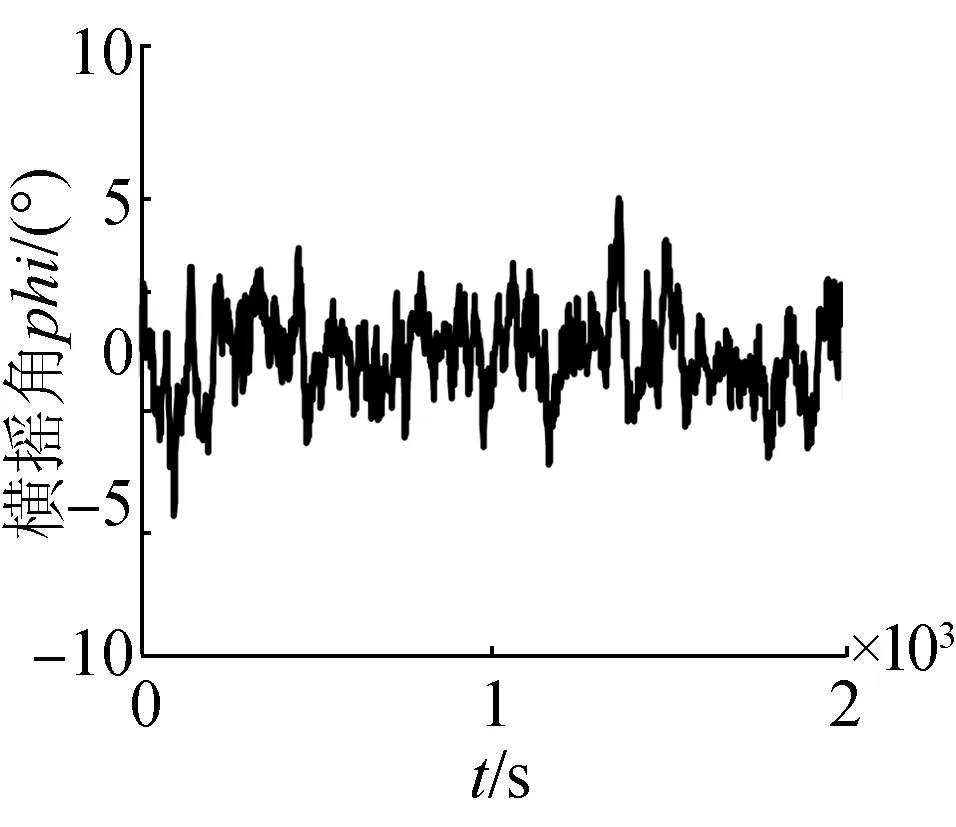
(d)橫搖角曲線

(e)縱搖角速率曲線

(f)縱搖角曲線

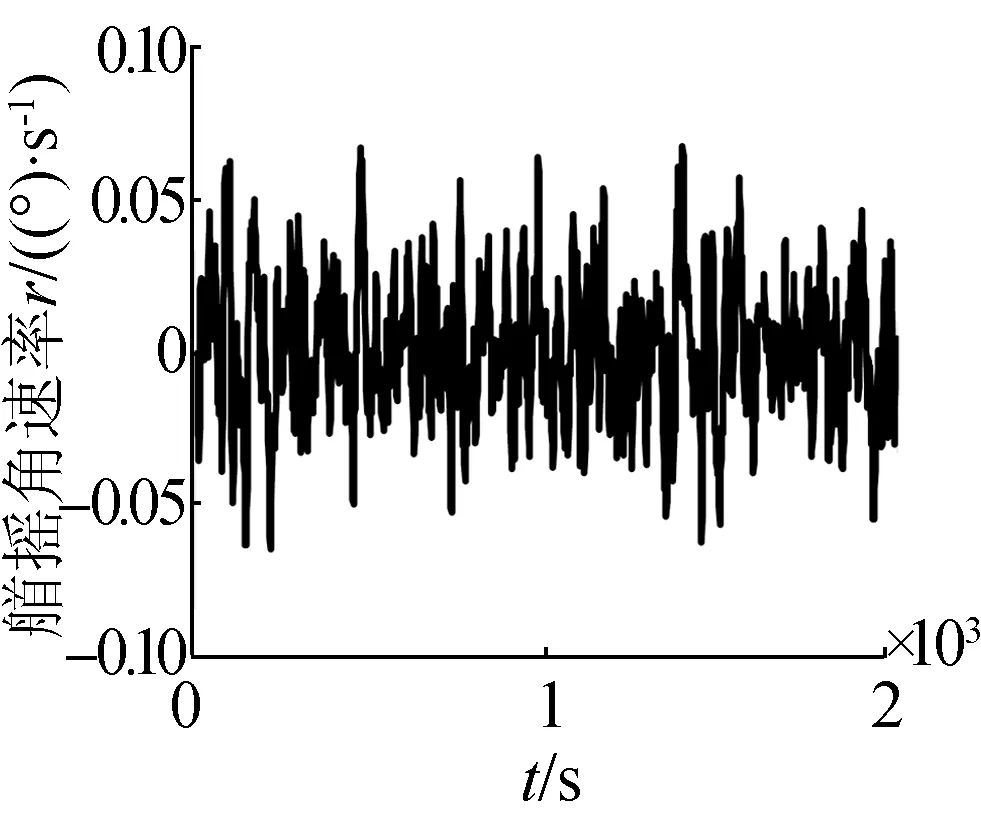
(g)艏搖角速率曲線

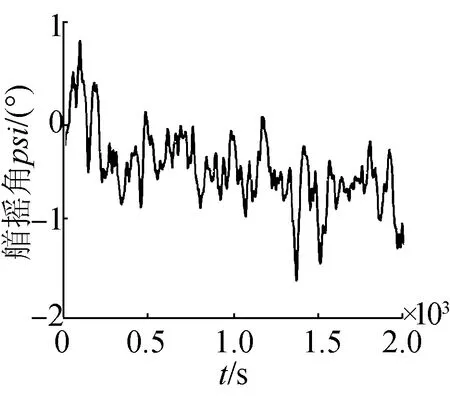
(h)艏搖角曲線

圖4中給出了在海浪干擾下潛艇直航運動的狀態。受海浪干擾力的作用，潛艇在水下直航運動時存在縱橫搖，其中橫搖角最大達到6°，縱傾角達7°。

保持上述仿真條件不變，將方向舵角改為20°，進行海浪干擾下，潛艇回轉運動的仿真，其運動軌跡及橫縱搖曲線如圖5所示。對比潛艇在靜水中回轉運動時的角速率及姿態角參數，在海浪干擾下，潛艇的橫向、縱向以及垂向角速度出現高頻的震蕩，相應的，其三維姿態角隨之變化，橫搖、縱搖較為明顯。

與圖4中的直航運動狀態比較，潛艇受回轉力和力矩的作用，其三維角速率變大，橫搖角不再以0°為中心上下震蕩，而是以-4°為中心上下震蕩，縱傾角出現高頻變化量。

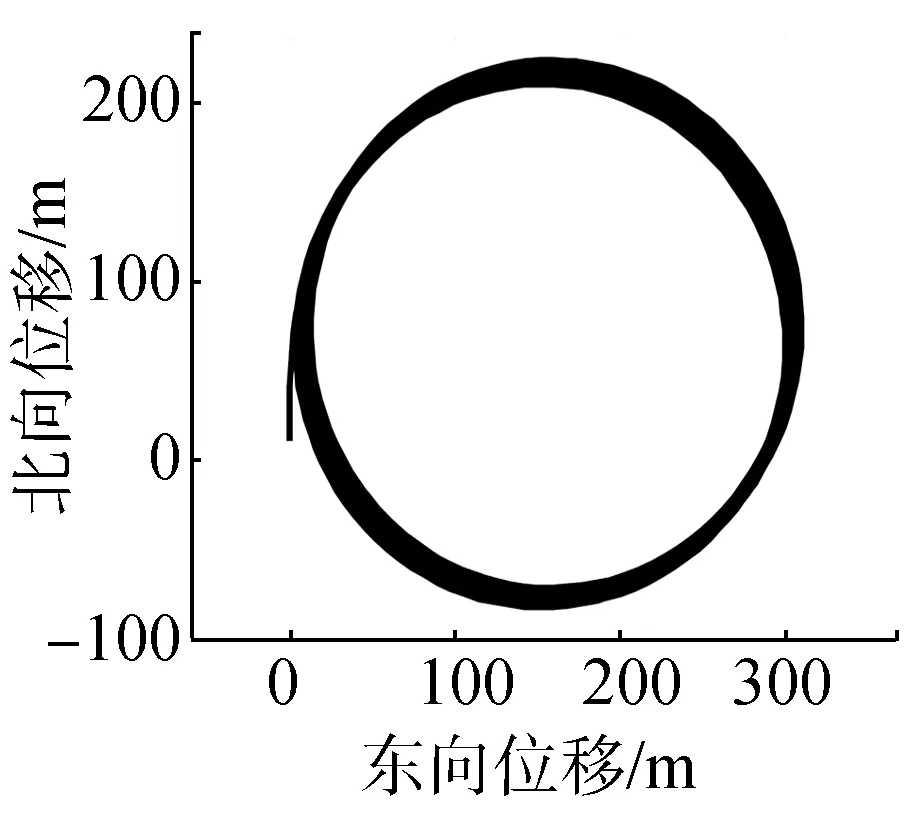
(a)運動軌跡

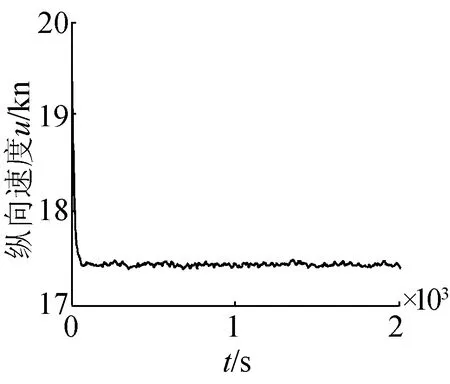
(b)縱向速度曲線

(c)橫搖角速率曲線

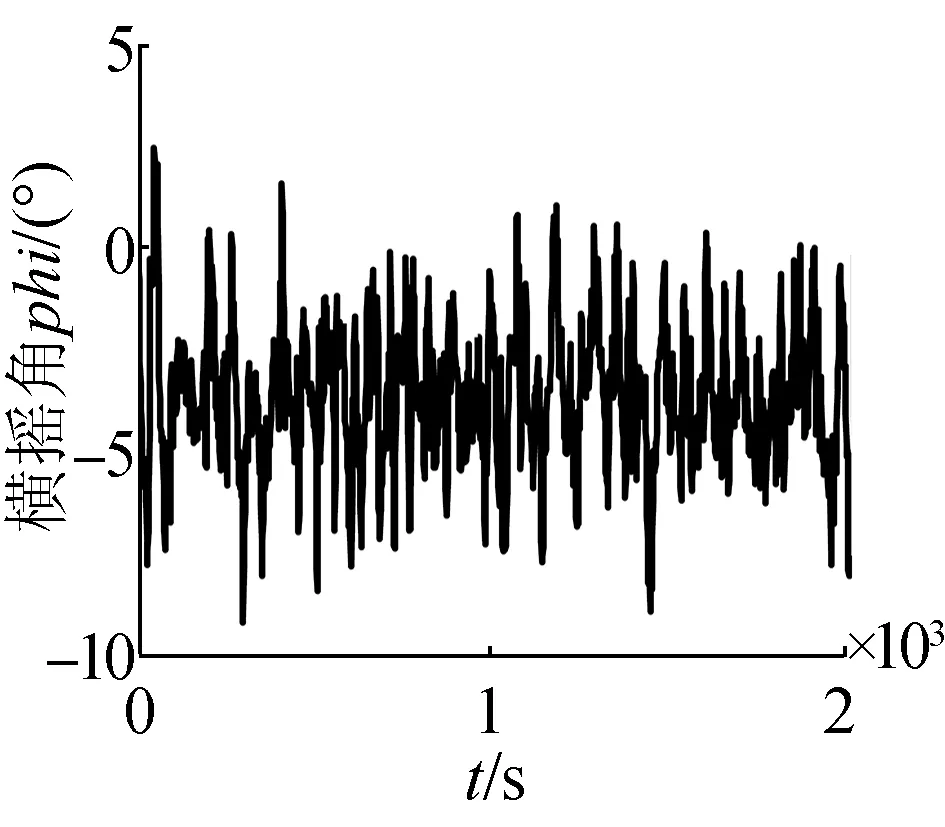
(d)橫搖角曲線

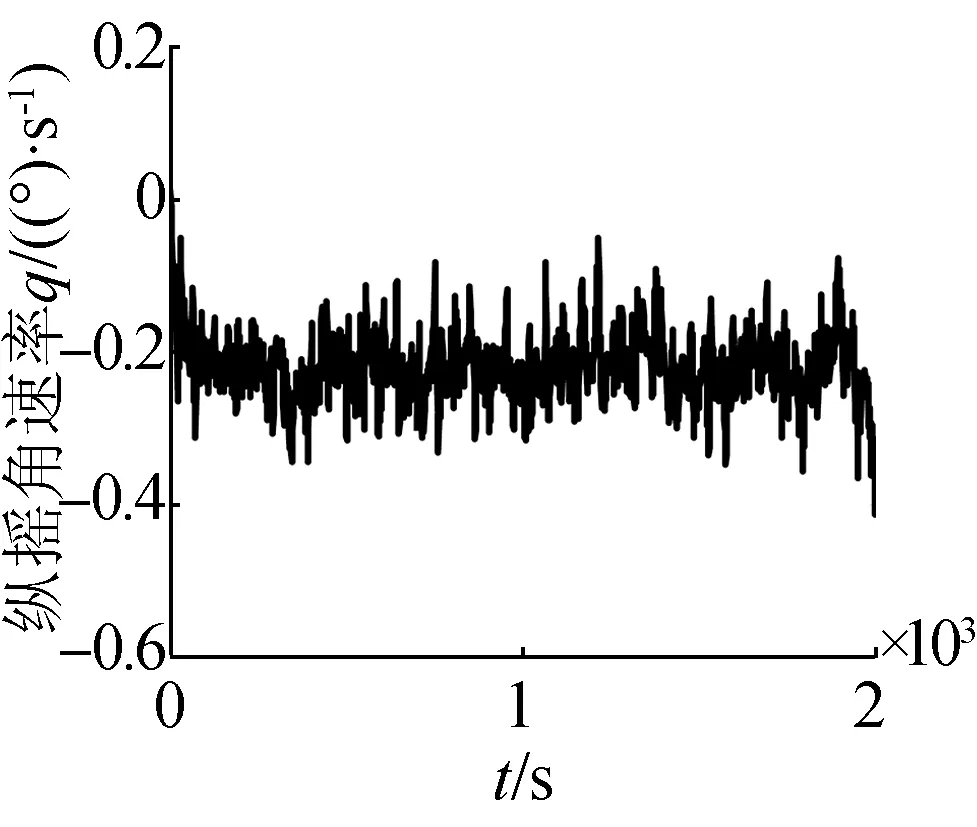
(e)縱搖角速率曲線

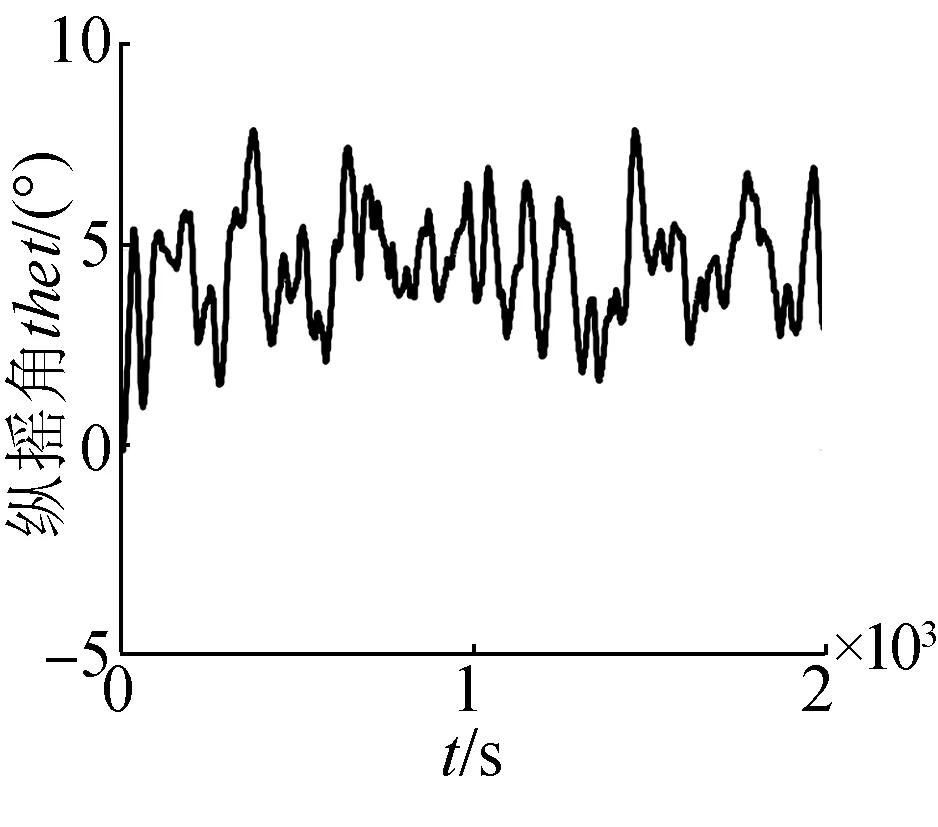
(f)縱搖角曲線

(g)艏搖角速率曲線

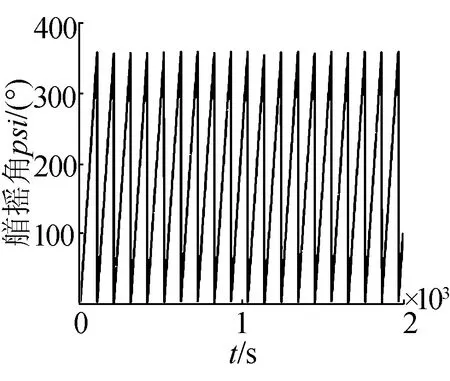
(h)艏搖角曲線

為了更進一步體現海浪對潛艇的作用效果，加強海浪干擾，將波高設置為3.25 m，潛艇的軌跡及橫縱搖曲線如圖6所示。

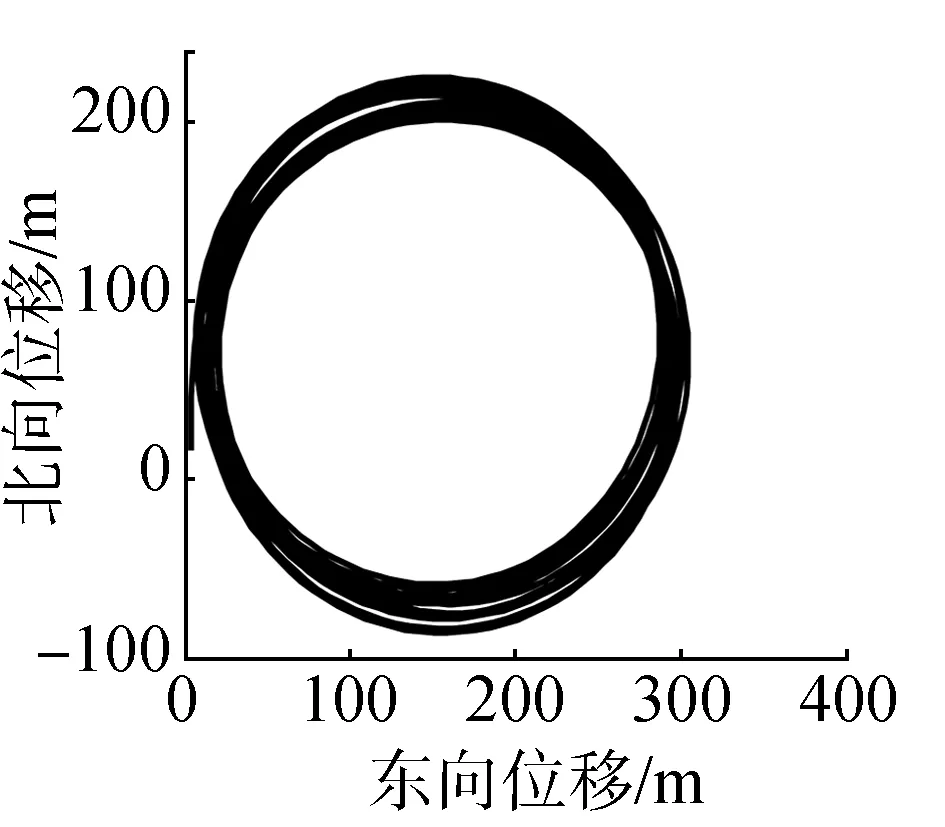
(a)運動軌跡

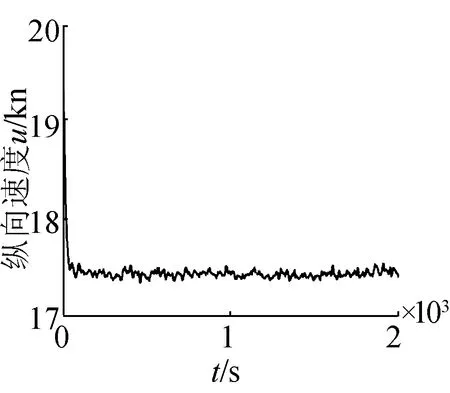
(b)縱向速度曲線

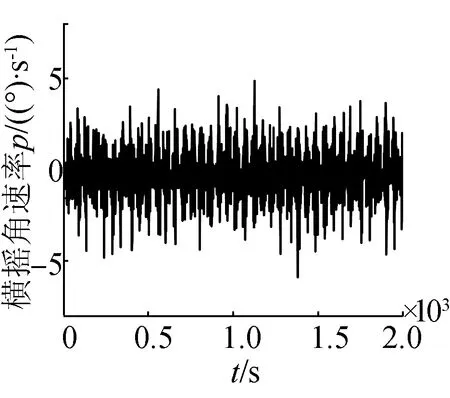
(c)橫搖角速率曲線

(d)橫搖角曲線

(e)縱搖角速率曲線

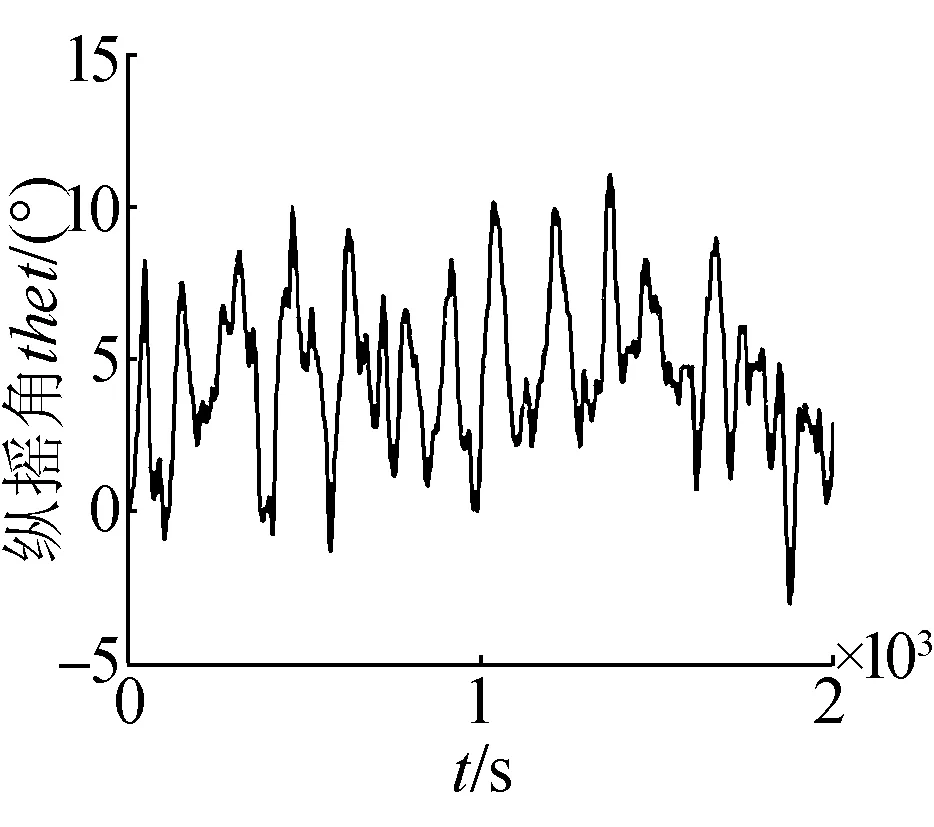
(f)縱搖角曲線

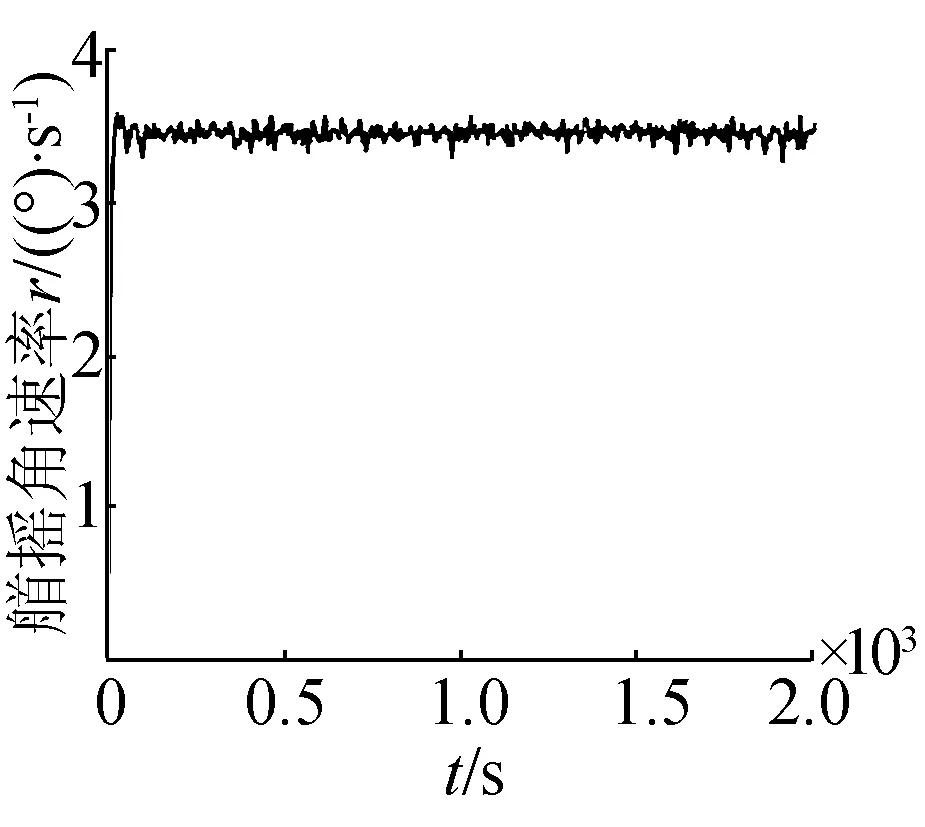
(g)艏搖角速率曲線

(h)艏搖角曲線

對比圖5，海浪的浪向保持不變，波高由1.28 m變為3.25 m，潛艇的三維角速率以及三維姿態角明顯變大，橫搖角及縱傾角高達11°。

3.3 海流對潛艇運動的干擾作用

本小節仿真了潛艇在不同等級海流下的直航和回轉運動。潛艇初始航速20 kn，調整螺旋槳推力使潛艇航速保持不變，航向角0°，正北航向，方向舵角為0°，首尾升降舵角設置為平衡，取首舵角為0.231 8°，尾舵角0.446 6°。其軌跡與速度曲線如圖7。

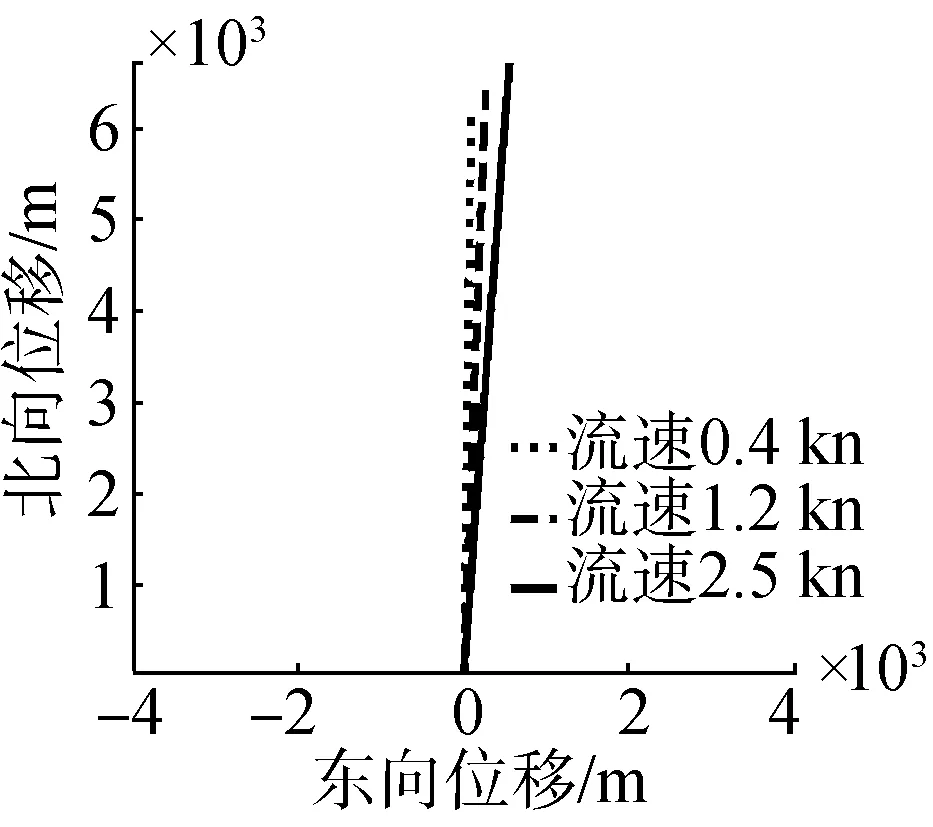
(a)運動軌跡

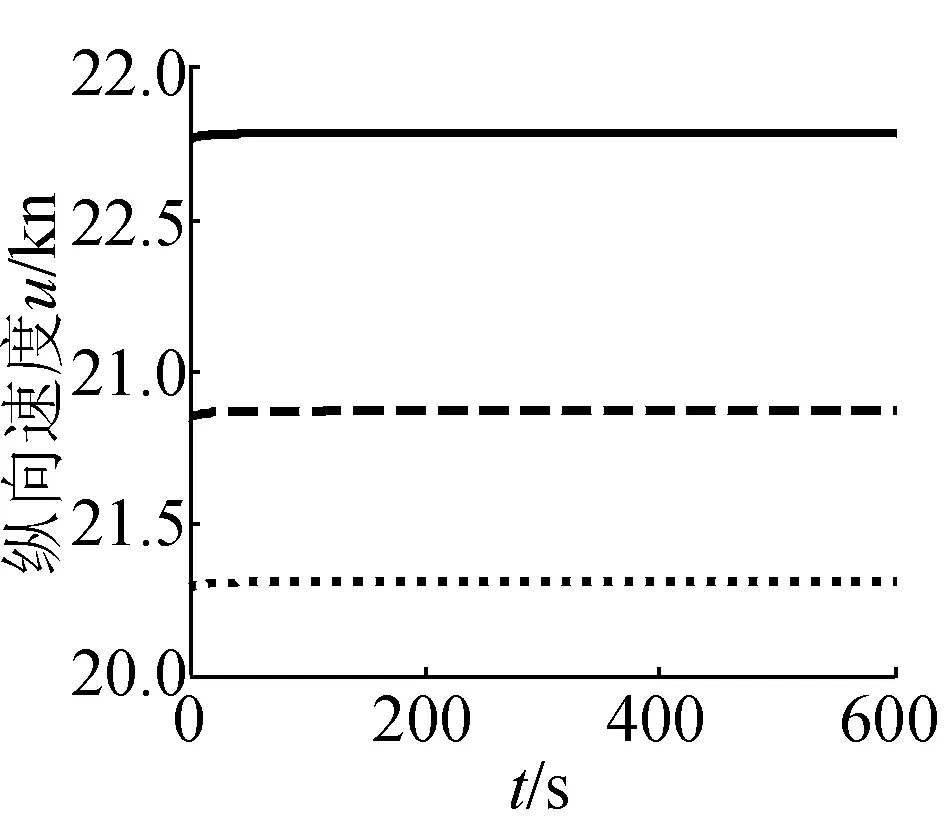
(b)縱向速度曲線

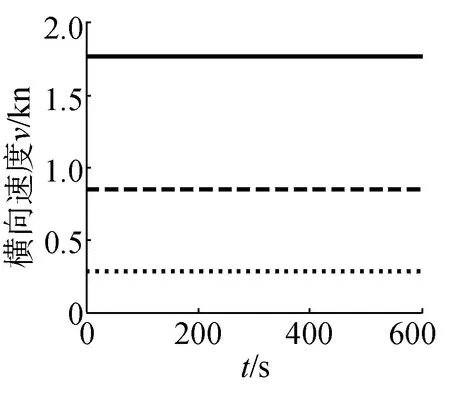
(c)橫向速度曲線

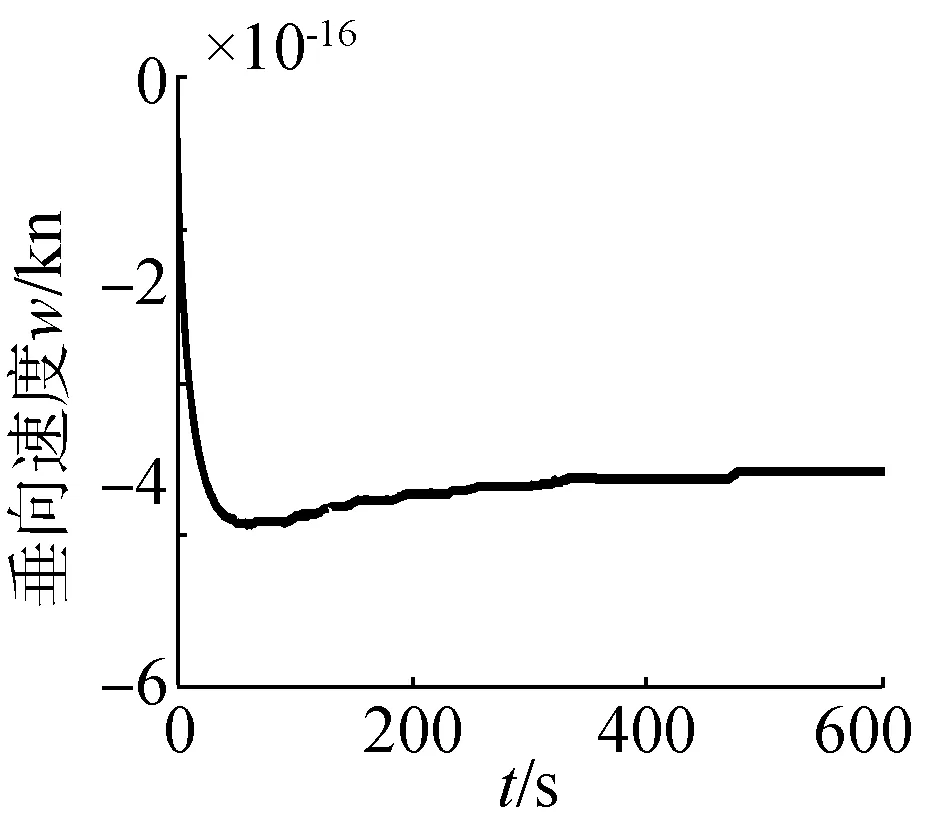
(d)垂向速度曲線

對于勻速運動的潛艇，海流的作用只是運動學上的。潛艇的初始速度是潛艇相對于海流的速度，潛艇相對固定坐標系的速度為潛艇相對于海流的速度加上海流的速度。根據海流方向及大小，流速1.20 kn，流向角45°時，可計算流速在船體縱向分量為0.849 kn，橫向分量為0.849 kn。潛艇縱向速度和橫向速度增量為流速的分量，由圖7可看出，潛艇橫向和縱向速度分量與流速在船體坐標系投影相等。對于潛艇的角速度及姿態角與靜水勻速直航時相同，海流不會引起它們的變化。

在上述仿真條件下，若將方向舵角設置為20°，對潛艇在不同海流下的回轉運動進行仿真，則其速度及運動軌跡如圖8所示。

(a)運動軌跡

(b)縱向速度曲線

(c)橫向速度曲線

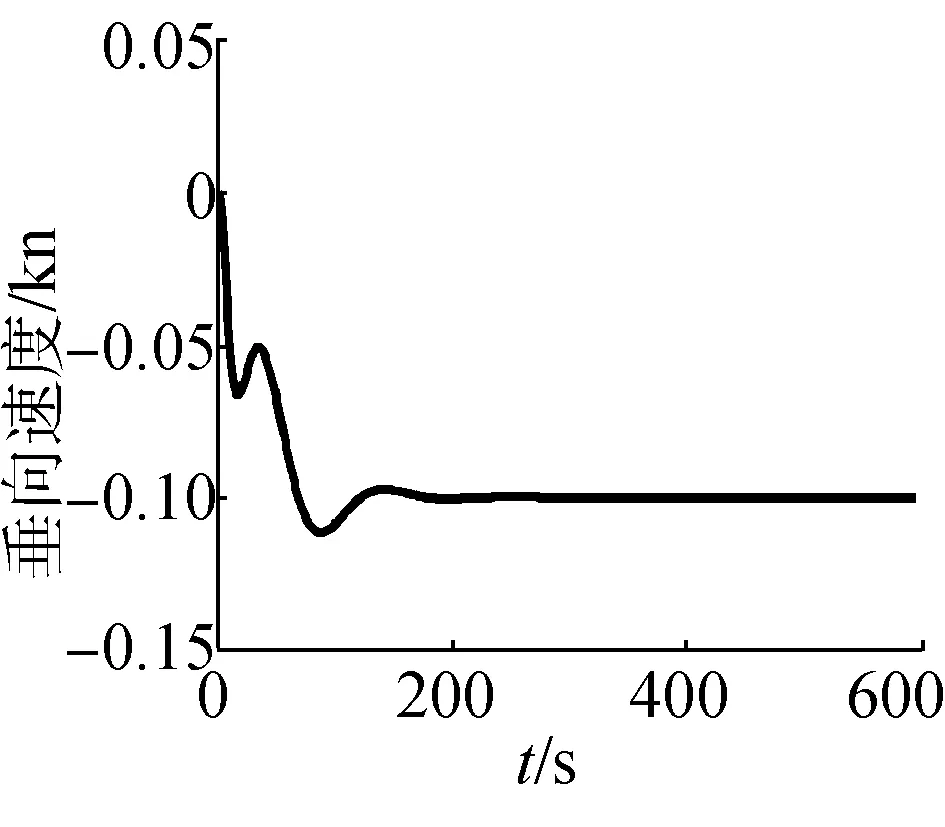
(d)垂向速度曲線

潛艇做回轉運動時，海流速度在艇體坐標系上的分量隨航向角的變化而做周期性的變化，故潛艇的縱向速度與橫向速度在速降后穩定在某一值處不斷周期變化。此外，由于潛艇相對于固定坐標系具有沿海流方向的速度，大小等于流速，故潛艇在做回轉運動時的回轉圈會沿海流方向漂移。

4 結束語

本文結合已有的經過實際試驗修正過的部分水動力系數，對潛艇在靜水及海況干擾下的回轉運動進行了仿真，通過定量設定仿真條件，定性分析了其運動軌跡、三維速率、角速率及三維姿態角的變化，將各種條件設置下的潛艇運動結果應用到敏感潛艇運動的導航系統的陸上性能鑒定中，從而為全面分析導航系性能提供了條件，一定程度上補充了實際海試條件的局限性。文中所用到的仿真對象某潛艇，因水動力系數有限，建立在許多假設條件上，是基于簡化的潛艇六自由度運動模型進行的仿真研究；對于海浪干擾的處理，采用海浪等級表中相關海浪參數，定性描述海浪大小；對于海流干擾的處理，因為缺少數據，只從運動學上考慮其對潛艇運動造成的影響，并不適用于潛艇高速運動，有待進一步研究改進。

[1]李玉東, 胡大斌, 陳勇, 等. 潛艇操縱控制系統仿真平臺設計與實現[J]. 艦船科學技術, 2013, 35(5): 123-127. LI Yudong, HU Dabin, CHEN Yong, et al. Design and realization of the submarine maneuver controlling system simulation platform[J]. Ship science and technology, 2013, 35(5): 123-127.

[2]施生達. 潛艇操縱性[M]. 北京: 國防工業出版社, 1995: 48-59. SHI Shengda. Submarine maneuverability[M]. Beijing: National Defence Industry Press, 1995: 48-59.

[3]吳秀恒, 劉祖源, 施生達, 等. 船舶操縱性[M]. 北京: 國防工業出版社, 2005: 60-62. WU Xiuheng, LIU Zuyuan, SHI Shengda, et al. Ship maneuverability[M]. Beijing: national defence industry press, 2005: 60-62.

[4]林雄偉, 胡大斌, 戴余良, 等. 潛艇操縱控制方法[J]. 艦船科學技術, 2013, 35(5): 7-10, 42. LIN Xiongwei, HU Dabin, DAI Yuliang, et al. Survey for maneuver control of submarine[J]. Ship science and technology, 2013, 35(5): 7-10, 42.

[5]時俊宇. 基于潛器空間運動的慣導系統適應性問題研究[D]. 哈爾濱: 哈爾濱工程大學, 2011: 23-26. SHI Junyu. The research of inertial navigation system adaptability based on underwater vehicle space motion[D]. Harbin: Harbin Engineering University, 2011: 23-26.

[6]朱怡. 潛艇航行訓練模擬器模型簡化與參數優化研究[D]. 哈爾濱: 哈爾濱工程大學, 2009: 45-47. ZHU Yi. The research on model simplification and coefficient optimization for submarine training simulator[D]. Harbin: Harbin Engineering University, 2009: 45-47.

[7]金濤, 楊楓, 王京齊, 等. 大攻角情況下破損進水潛艇水下機動性[J]. 華中科技大學學報: 自然科學版, 2008, 36(12): 79-82. JIN Tao, YANG Feng, WANG Jingqi, et al. Submerged maneuverability of flooded submarine with large angle of attack[J]. Journal of Huazhong university of science and technology: nature science edition, 2008, 36(12): 79-82.

[8]王彥磊, 袁博, 朱尚卿, 等. 海洋環境對潛艇活動的影響[J]. 艦船科學技術, 2010, 32(6): 52-55. WANG Yanlei, YUAN Bo, ZHU Shangqing, et al. The influence of marine environment on submarine activities[J]. Ship science and technology, 2010, 32(6): 52-55.

[9]OSTAFICHUK P M. AUV hydrodynamics and modelling for improved control[D]. Vancouver, Canada: The University of British Columbia, 2004: 78-81.

[10]戴余良. 潛艇在隨機海浪中搖蕩運動的仿真研究[J]. 計算機仿真, 2001, 18(5): 42-45. DAI Yuliang. Simulation study on swaying movement of a submarine in random ocean waves[J]. Computer simulation, 2001, 18(5): 42-45.

[11]SEO M G, KIM Y. Effects of ship motion on ship maneuvering in waves[C]//Proceedings of the 26th International Workshop on Water Waves and Floating Bodies. Athens, Greece, 2011.

[12]豐少偉, 戴余良, 陳志法. 潛艇水下回轉運動穩定性分析[J]. 指揮控制與仿真, 2015, 37(1): 74-79. FENG Shaowei, DAI Yuliang, CHEN Zhifa. Analysis of motion stability of submarine s underwater rotational movement[J]. Command control & simulation, 2015, 37(1): 74-79.

Analysis of six-degree-of-freedom motion in submarines under sea disturbance

LI Hui，ZHAO Lin，MAO Ying

(College of Automation, Harbin Engineering University, Harbin 150001, China)

In order to compensate for the limitations of actual conditions in sea experiments, and to test on land the equipment that can be affected in a submarine motion, in this paper, we investigate a six-degree-of-freedom motion of submarines, including the submarine’s direct navigation and turning movements in still water and the marine environment. By analyzing the force of a moving submarine using the basic model of ocean waves and currents, we established a six-degree-of-freedom motion equation of submarines under ocean wave disturbance. Based on a submarine’s hydrodynamic coefficients, which we collected and then corrected in our experiments, we could determine the submarine’s line and angular movements, and could thus analyze its direct and turning movements. Simulation results can realistically reflect the interference in the movement of submarines in the marine environment, and thus meet the need in practical engineering to test equipment.

submarine; motion model; six-degree-of-freedom; marine environment; ocean wave disturbance; ocean current disturbance

2015-11-13.

時間：2016-12-12.

國家自然科學基金項目(61273081).

李慧(1987-), 女, 講師,博士研究生； 趙琳(1968-), 男, 教授,博士生導師.

李慧, E-mail：lihuiheu@hotmail.com.

10.1190/jheu.1006-7043.201511027

U675.9; U666.12

A

1006-7043(2017)01-0094-07

李慧, 趙琳, 毛英.海況干擾下潛艇六自由度運動分析[J]. 哈爾濱工程大學學報， 2017, 38(1): 95-101. LI Hui，ZHAO Lin，MAO Ying.Analysis of six-degree-of-freedom motion in submarines under sea disturbance[J]. Journal of Harbin Engineering University, 2017, 38(1): 95-101.

網絡出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20161212.1632.036.html