船只補給懸鏈線系統運動特性分析

吳衛國 ,譚振東,王振濤,冷永剛,杜尊峰

(1.天津大學 機械學院, 天津 300072； 2.軍事交通運輸研究所, 天津 300161； 3.天津市科委, 天津 300051 ； 4.天津大學 水利工程仿真與安全國家重點實驗室,天津 300072)

船只補給懸鏈線系統運動特性分析

吳衛國1,2,譚振東3,王振濤2,冷永剛1,杜尊峰4

(1.天津大學 機械學院, 天津 300072； 2.軍事交通運輸研究所, 天津 300161； 3.天津市科委, 天津 300051 ； 4.天津大學 水利工程仿真與安全國家重點實驗室,天津 300072)

船只索道補給越來越廣泛用于兩船或船岸之間物資傳送，本文綜合考慮船只與錨泊系統的耦合以及船只運動對索道的影響，通過計算波浪中船只補給懸鏈線系統的動力學響應，得到了船只補給懸鏈線系統的運動特性，為系統設計提供依據。運用索道懸鏈線理論和有限元方法，對模型進行了計算，并對數值模擬結果和理論結果進行了比較。結果表明：數值模擬結果和理論結果整體吻合較好；三級海況下，連接設備時應將船只側面對著固定物，連接點應在船只的中心線上。高海況條件下，應考慮垂蕩的影響，理論模型簡化因素較多，索道跨距80 m之后，應以仿真分析模型為主。

船只補給；懸鏈線系統；運動特性；動力學響應；有限元方法

隨著海洋開采技術的發展，許多大的石油或天然氣平臺逐步出現，使得海上大型浮體結構的設計研究成為熱點問題，其中浮體和浮體之間的連接技術又是一個關鍵性問題。在此方面，許多研究者研究了相連浮體的水作用響應[1-2]。Fang等[3]采用二維切片法計算了兩平行布置的條狀浮體間的水動力相互作用。Duncan等[4]采用Oortmerssen[5]的方法計算了兩船體的運動響應，并在計算中考慮了錨泊纜和防碰墊的作用。Chen and Mahrenholtz用邊界元的方法，討論了兩漂浮圓柱之間的連接剛度、間距及水深等參數的變化對圓柱運動響應的影響[6]。Newman[7]采用邊界積分的方法，對兩個相同的均質方箱在固接和鉸接情況下的運動響應進行了數值計算。沈慶等[8]對于鉸聯結系泊多浮體系統，將其作為鉸聯結無根樹系統，用多剛體力學方法進行了運動學分析。勾瑩等[9]應用邊界積分方程方法研究了波浪與2個相連三維浮體的相互作用問題，計算中考慮了浮體相互間的水動力干涉, 通過聯立各浮體的運動方程以及運動連續條件求得浮體運動量。Hong等[10]通過數值計算研究系泊多浮體運動響應特性。Sun等[11]基于線性繞射理論，并采用拉格朗日乘子方法，探討了兩浮體在鉸接、固接、彈性連接情況下的運動響應以及不同連接形式下連接點的受力情況。劉文璽等[12]在浮體和系泊系統的時域耦合分析中，將浮體的分析方法和系泊纜索的分析方法結合，建立了浮體和系泊系統非線性運動響應和纜索張力的耦合計算方法。許鑫等[13]對目前海洋工程中較為常見的多浮體系統進行了介紹，并就國內外在多浮體系統的水動力方面的研究進行了系統的闡述。

目前，浮體與浮體在水作用力下相互作用的研究已達到一定深度，但是關于浮體和固定物體連接作用的研究還不多見，尤其是船只與固定物體連接的動力學響應研究則更是鮮見報道。

1 船只補給懸鏈線系統理論分析

船只補給懸鏈線系統是由船只、懸鏈線與固定物體組成。懸鏈線連接一般為索道連接，本文中懸鏈線統一稱為索道。船只補給懸鏈線連接主要用于海上浮體與相對靜止設施之間的物資和人員傳送，它區別于浮體與浮體連接，表現為連接的功用不同，連接的方式不同，連接的距離也有差別。此外，船只補給懸鏈線系統的連接方式也不同于山地叢林的索道連接方式[14]，山地叢林索道主要是在固定的物體上展開。艦船補給索道連接[15]在艦船航行補給時，兩船處于航行狀態，保持適當的航速, 并利用操舵裝置產生橫向力, 抵消索道張力, 維持一定的船距。

船只對固定目標補給時要求船只在錨泊狀態下僅通過索道連接固定目標，索道只能依靠補償裝置自身來控制。具體連接工作方式是：帶有補給品的船只當接近固定目標時，應在開闊的水域內錨泊確定其位置，如圖1中的浮體。而后人員在船只上拋送繩索一端到固定物目標上，將繩索與固定物的某處位置連接，然后繩索的另一端與船只連接，并通過恒張力補償裝置將繩索收緊，實現船只和固定物的索道連接。船只水線以上部分會受到風載作用，而船只水線以下部分會受到海流作用，船只受到的這兩種作用載荷由船只拋錨的錨鏈力進行平衡，使船只在平衡位置附近漂浮運動。船只在水中漂浮運動時，索道會出現拉緊或松弛，系統中恒張力補償裝置自動收放索道使得索道處于張緊狀態，從而保持恒定張力。這里恒張力補償裝置如何得到索道跨距以及補償量等參數并嚴格控制索道張力，相關研究可見文獻[16]，本文只考慮船與固定物之間相對運動時(靠近或者離開)纜的張力基本保持恒定，以確保物資能夠在船只和固定物之間保持平穩運送的情況。

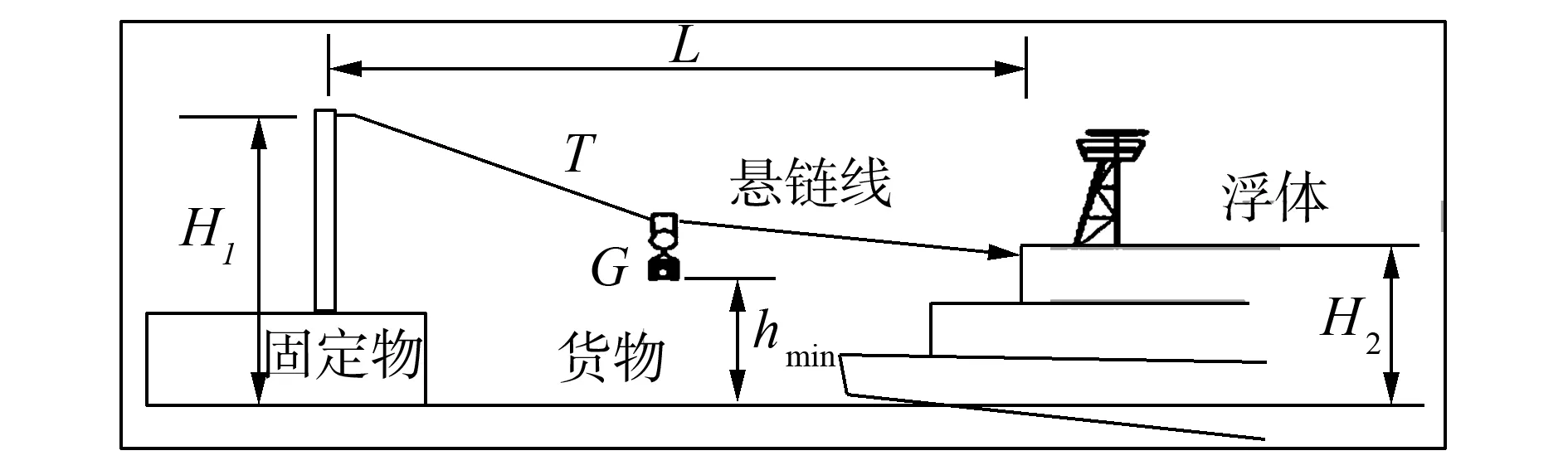
圖1 船只和固定物的連接方式示意圖Fig.1 The connecting way of vessel and fixation object

船只和固定物之間有一定的距離空間，二者通過懸鏈線相互作用。船只和固定物的距離變化與兩個船只或浮體間的距離變化是不同的，兩個船只間或浮體間的距離是通過航行或運動來保持。而固定物和船只的距離是通過船只拋錨固定的受力平衡方式保持。因此有必要研究船只錨泊情況下的波浪運動響應，為船只補給懸鏈線系統分析奠定基礎。

1.1 船只運動分析

1.1.1 船只運動平衡位置及穩定性分析

船只在波浪中受到風、浪、流引起的力以及力矩的作用如圖2所示。

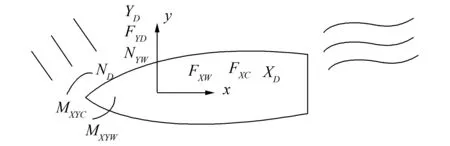
圖2 船只受力分析示意圖Fig.2 The analysis of vessel forces

作用在船只的縱向總載荷FXT、橫向總載荷FYT及總搖艏力矩MXYT分別為

(1)

式中：FXW是縱向風力，FYW是橫向風力，FXC是縱向流力，FYC是橫向流力，XD是縱向二階波浪漂移力，YD是橫向二階波浪漂移力，MXYC是流的搖艏力矩，MXYW是風的搖艏力矩，ND是漂移力的搖艏力矩。

對于單點系泊船只，平衡位置的計算方程為

(2)

式中：∑M為合力矩，ARM為船只中心和船艏系索點處的距離(一般取ARM=0.48LOA)，LOA為總船長。

1.1.2 船只三維運動響應

船只在水中的三維運動響應主要是受到不規則波的作用，這種不規則波可被分解成為多個規則子波進行處理，通過三維格林函數法計算規則波中船只的運動響應，然后進行疊加就可以得到船只總體三維運動響應。在不規則波的多規則波分解中，頻率為n規則波能夠被獲得，命名為ωi，i=1,2，…,n。

(3)

(4)

式中：MS為質量矩陣，A為附加質量矩陣，B為阻尼系數矩陣，KW為恢復力系數矩陣，Fe為激勵力，CS為粘性阻尼，從試驗或經驗公式中獲得，KL是纜索的剛度矩陣。通過三維格林函數計算船只在規則子波的運動，然后再進行疊加，進而得到船只在不規則波的運動響應。

1.1.3 船只與錨泊鏈耦合動力分析

在對船只與錨泊鏈耦合動力分析中，船只的水動力學特性采用三維勢流理論進行求解。船只的拖拽力采用莫里森公式進行計算分析，錨泊線的動力分析采用桿理論和有限元模型，在總體坐標系中建立控制方程進行計算，錨泊線和補給船舶之間的連接采用平動、轉動彈簧以及阻尼器進行模擬，通過調整彈簧和阻尼器的控制參數可以模擬各種形式的連接，船只和錨泊線耦合系統的方程，如下所示

(5)

式中:KL是錨泊線和彈簧(阻尼)連接器的聯合剛度矩陣，KB是剛度矩陣，KC和KCT分別是包含船只和錨泊線耦合項的耦合剛度矩陣及其轉換矩陣，UL和UB分別是錨泊線和船只的位移列陣，FL和FB分別是作用在錨泊線和船只上的力列陣和力矩列陣。

1.2 懸鏈線(索道)計算分析

索道受力的計算理論主要有懸鏈線理論和拋物線理論，研究高架索道特性的方法主要有近似法和精確法；拋物線理論假定垂向載荷沿水平方向均勻分布，懸鏈線理論假定垂向載荷沿著索道長度弧度方向均勻分布。當索道只受到重力時，線的真實形狀應該是懸鏈線[17-18]。根據文獻[18]可得到索道懸鏈線的力學分析模型。

1.2.1 無載荷索道計算模型

鋼索在跨度內沿長度方向均勻分布，以鋼索最低點為原點建立直角坐標系，見圖3。

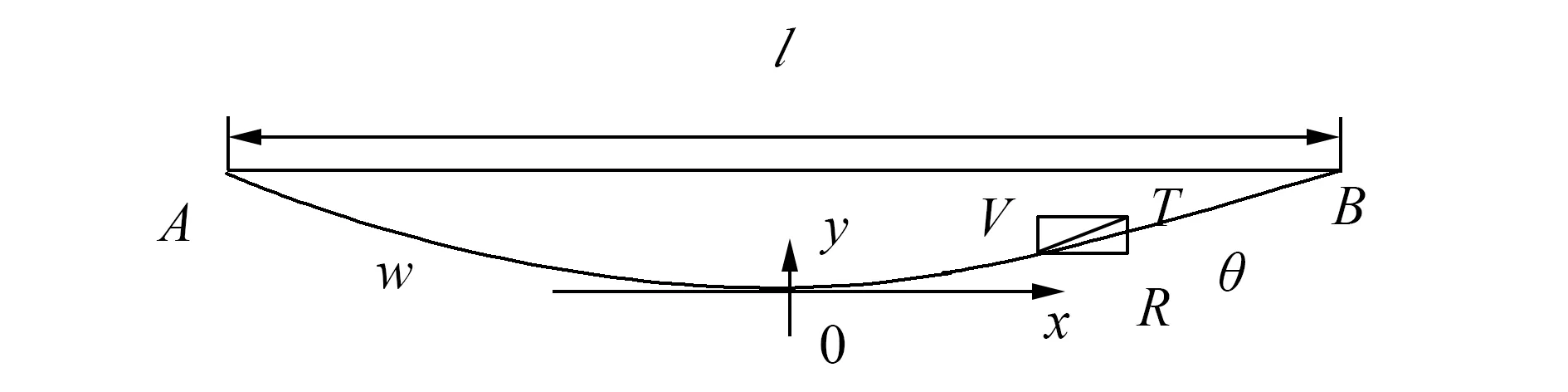
圖3 鋼索曲線受力分析圖Fig.3 The analysis of ropeway forces

懸鏈線的方程是一個雙曲余弦函數，其方程形式為

(6)

式中：R為無載荷索道鋼索受到的水平分力，w是懸鏈線即鋼索的單位長度重量，懸鏈線的斜率角θ。

(7)

鋼索各點受到的拉力T為

(8)

1.2.2 考慮集中載荷的作用

集中載荷是通過貨物的重力引起的，貨物重力Q作用在鋼索時，其受力可表示為

(9)

(10)

式中：R為有荷載索道受到的水平拉力，Ta為有荷載索道AD段的平均拉力，Tb為有荷載索道DB段的平均拉力，k為AD的距離與DB距離的比值；l0為A、B支點的水平跨距，TB為有荷載索道AD段最低點的水平坐標，TL為有荷載索道DB段最低點的水平坐標，TR為有荷載索道AD段的懸鏈線長度，L2為有荷載索道DB段的懸鏈線長度。

1.3 綜合運動分析

船只在波浪中的運動受到風、浪、流等影響較大，運動響應也與船只的類型有關，在低海況條件下，船只偏離平衡位置的距離通過索道的張緊裝置得到補充，索道連接點的位置也變化較小，因此，低海況條件下，計算其綜合運動時，可考慮索道長度的變化，忽略船只運動對索道的其他影響。連接索道受力分析模型如圖4所示，根據文獻[19]可以得到貨物的運動方程。

圖4 船只補給懸鏈線系統的計算模型Fig.4 The calculation model of vessel supply catenary system

貨物沿索道運動的軌跡為[19]

(11)

式中：q為鋼索的單位長度質量，h為A、B兩點的高度差，Q為貨物(包括吊鉤等)重力，β為AB與水平方向的夾角，H為鋼索的水平方向的分力，L為索道跨距，C0為常數。

貨物運動方程為[19]

(12)

式中：m為貨物(包括吊鉤等)質量；c為阻尼系數，c=2ζω0m；ζ為無量綱阻尼比；αL和αR為如圖4所示的PA、PB與水平方向的夾角，L0為A點和Q點的水平距離。

當x為L/2時，撓度最大，從式(11)可得最大撓度fmax與水平力H的關系為

(13)

由分析知：隨著索道跨距的增加，最大撓度也隨著增大，貨物有可能落水；高度差h越大，最大撓度減小，最低點縱坐標值越小，即離水面越遠；索道水平力與最大撓度成反比關系，索道張力越大，最大撓度越小，但是對索道的要求越高。因此，必須控制索道的跨距大小，保持兩端一定的高度差，確保張力在安全范圍內，這樣才能安全運輸物資。下面將對船只及懸鏈線系統的運動進行仿真分析。

2 數值仿真模擬

船只與固定物的連接，可以以運輸船和海上石油平臺為例。大型石油平臺相對較大，可考慮為固定物。考慮到運輸船和平臺連接的安全性，連接設備在三級海況下展開，運輸船的型深為4.7 m，非滿載下，輕載狀態時的高度為4.3 m，船舶吃水為1.955 m，懸掛點的高度為7.05 m，坐標系的原點建立在吃水線平面，船舶被分成20個部分，在每個部位均用面單元建立網格，運輸船的模型見圖5。三級海況下的環境載荷見表1，通過仿真模擬得到三級海況下運輸船的運動位移、速度和加速度，結果見表2～4。三級海況下的運輸船耦合運動分析結果見圖6。

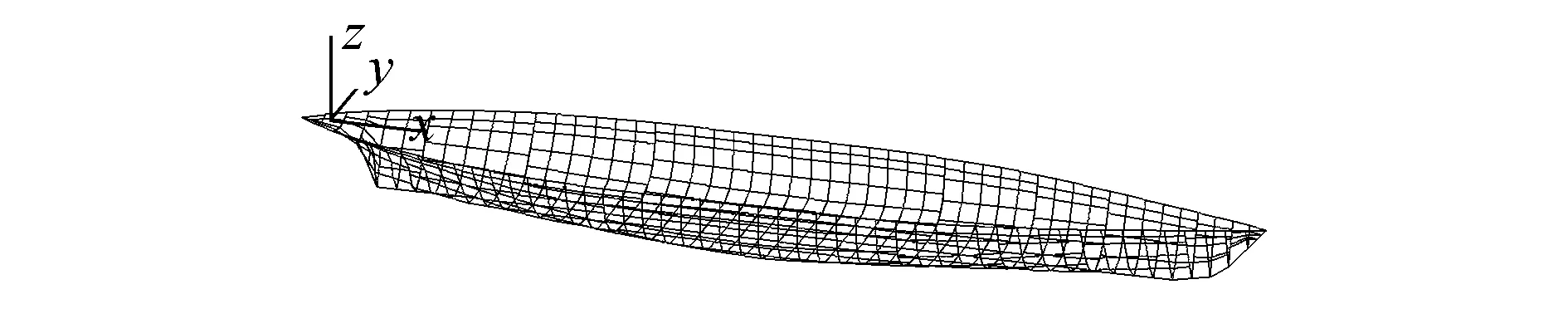
圖5 運輸船網格Fig.5 The grid of carrier

三級海況的環境載荷見表1。

表1 三級海況環境載荷

表2三級海況下的運動位移

表3 三級海況下的速度

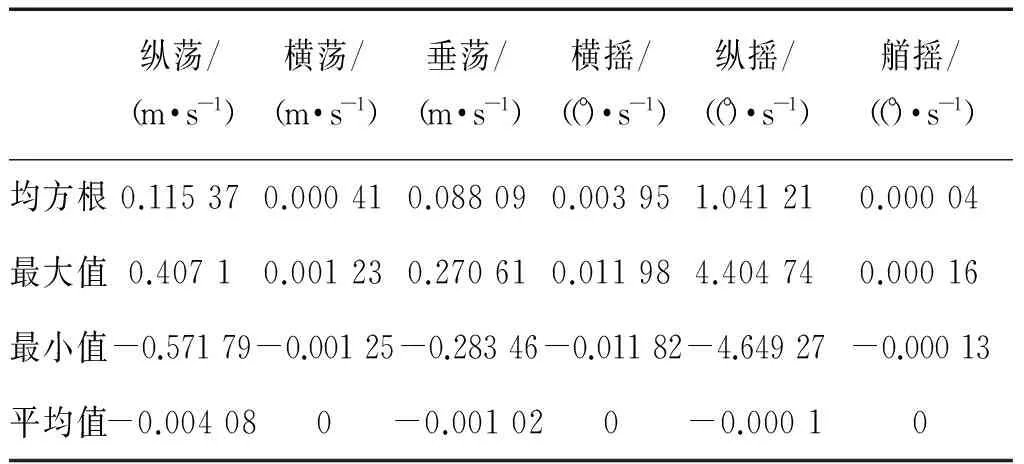
表4 三級海況下的加速度

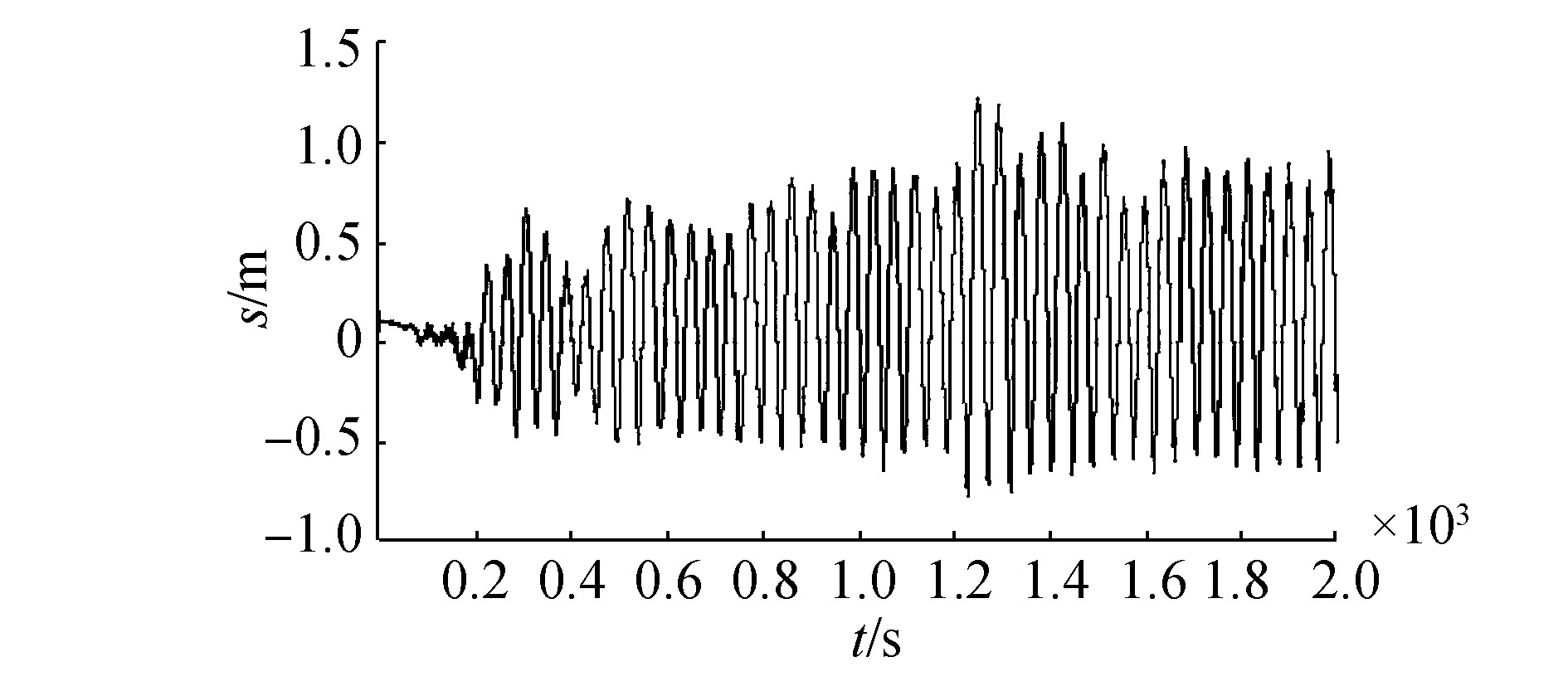
(a)運輸船的縱蕩

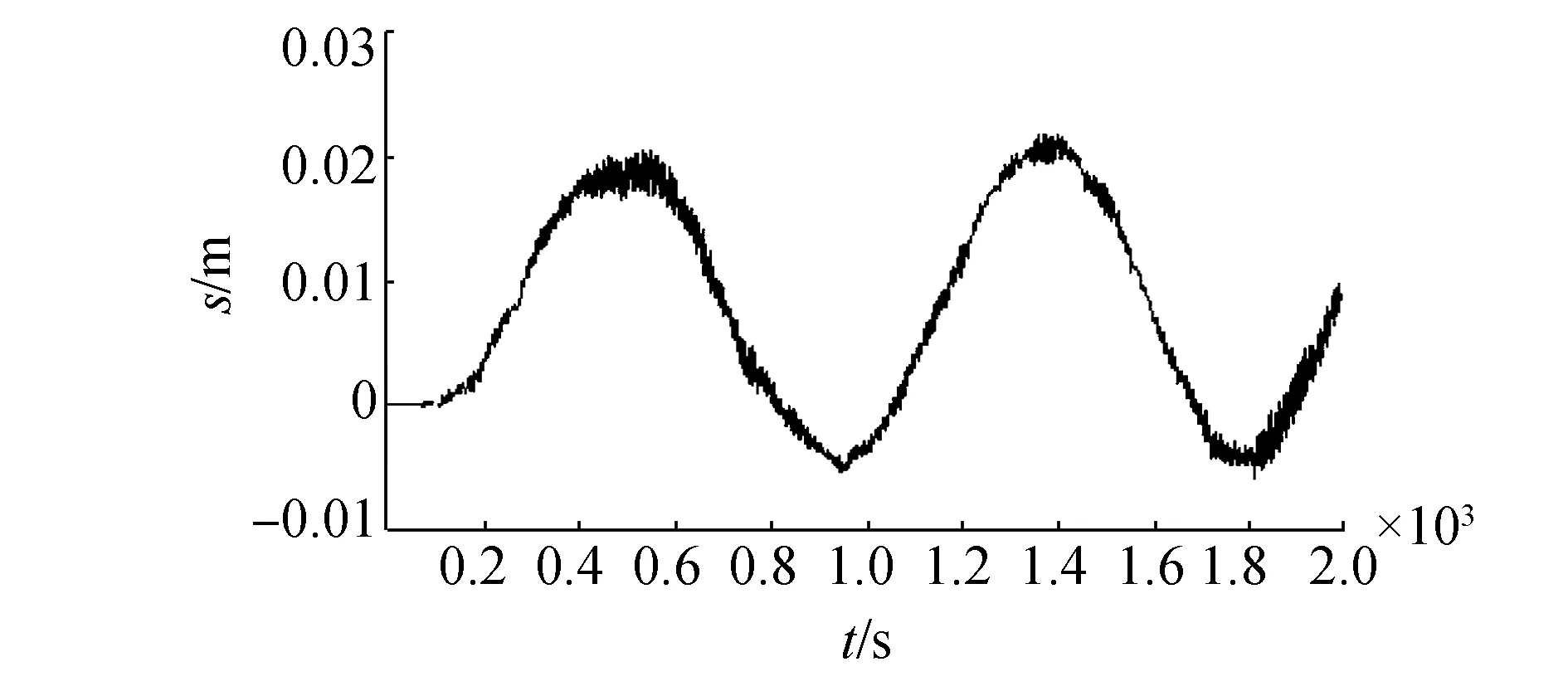
(b)運輸船的橫蕩

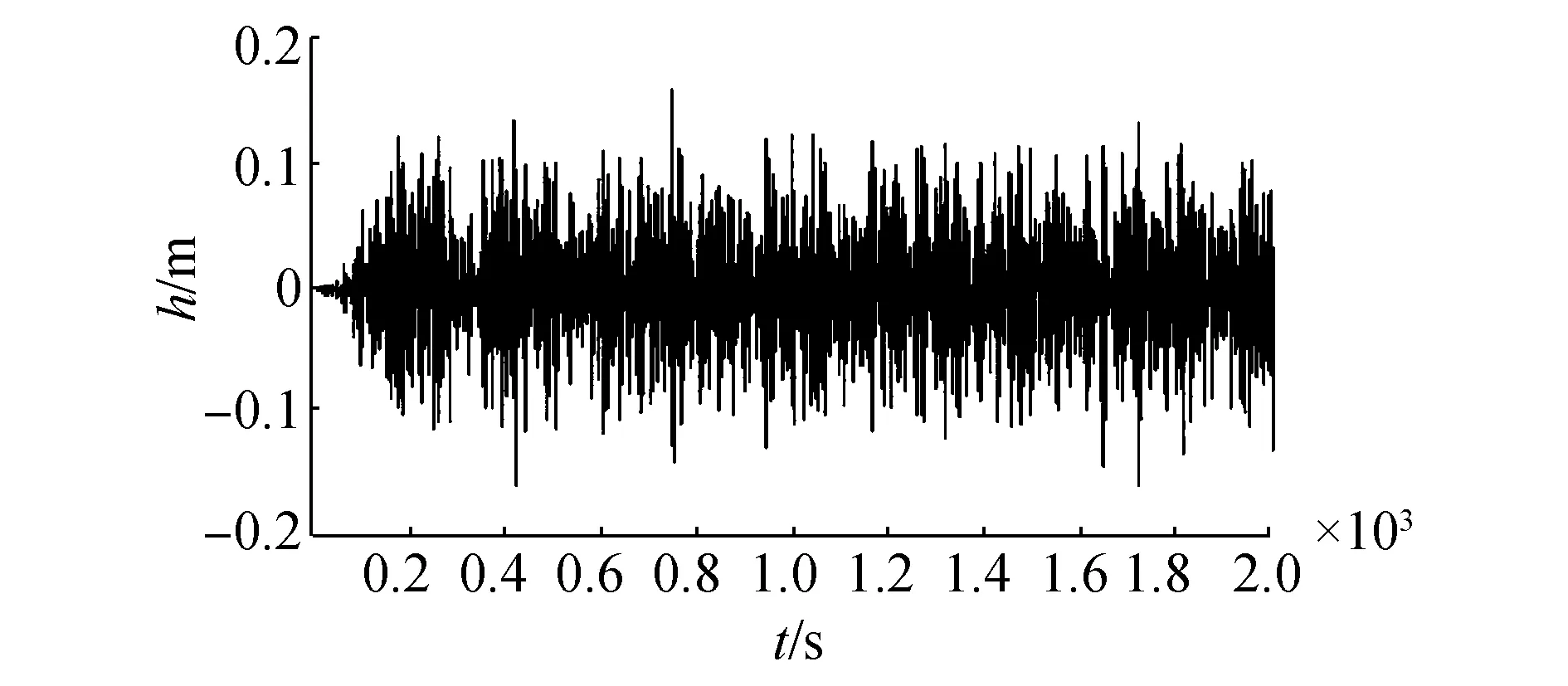
(c)運輸船的垂蕩

(d)運輸船的橫搖

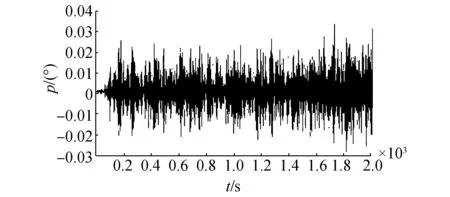
(e)運輸船的縱搖

(f)運輸船的艏搖圖6 三級海況下的運輸船耦合運動分析結果Fig.6 The analysis result of coupling motion at the level 3 sea states

由分析可知，三級海況下，對船只和固定物連接影響較大的因素為縱蕩和縱搖，縱蕩的最大值可達到1.2 m，縱搖的速度達到2.5 m/s，縱搖加速度達到4.4 m/s2，這對索道連接是極其不利的。因此，在連接設備時應該使船只側面對著固定物，連接點應該在船只的中心線上，降低縱蕩和縱搖對索道的影響。垂蕩會引起連接點位置的變化，在三級海況下垂蕩的最大值為0.15 m，對連接點位置影響較小，可忽略其影響，在高海況條件下，應考慮該因素。

在考慮了錨泊系統耦合運動后，船只的運動較為復雜，在做周期運動的同時，也會隨著錨鏈的影響做小范圍運動，運動的幅度較小，對于索道的連接影響較小，但要注意錨的位置變化，高海況下，會發生走錨的現象，對于船只與固定物的連接較為不利。

連接繩索的跨距分別取40、60、80 m，三個索道的參數為：16、12、12 mm，繩索的長度為100、200、100 m。16 mm的索道單位質量為0.99 kg/m，其他類型的繩索單位質量為0.6 kg/m，貨物的重量為50 kg，通過理論計算得到不同跨距下拉力及其撓度，見表5。

表5 不同跨距下索道拉力及其撓度

Table 5 The ropeway tension and deflection in the different ropeway spans

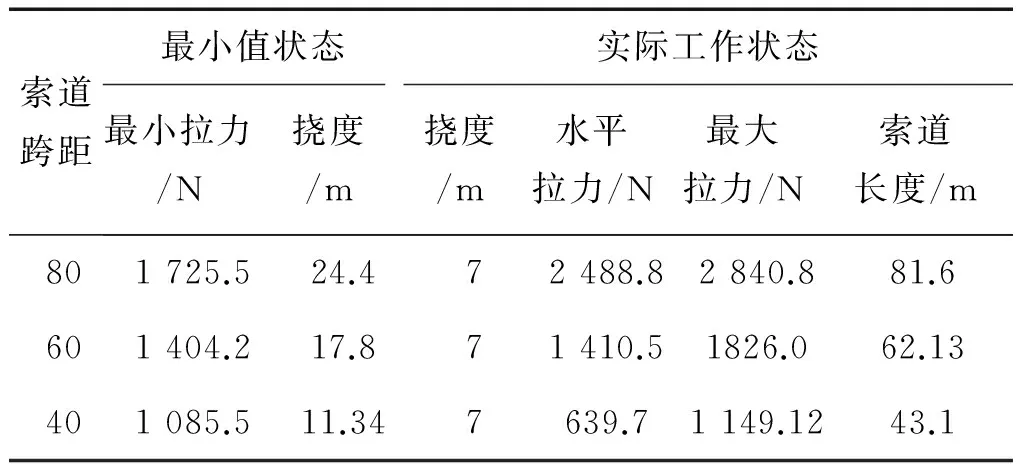
索道跨距最小值狀態實際工作狀態最小拉力/N撓度/m撓度/m水平拉力/N最大拉力/N索道長度/m801725.524.472488.82840.881.6601404.217.871410.51826.062.13401085.511.347639.71149.1243.1

從表5來看，張力變化幅度隨著撓度增大而減小。在相同的撓度時，張力隨著距離的增大而減小。

下面在ansys中模擬索道的連接，索道采用Beam 188單元建模，等效截面為9.5 mm，鋼索密度為7.85 t/m3，重力加速度為9.8 m/s2，兩端采用絞支，如圖7所示。仿真時接收索必須同放索保持相同速度，考慮到貨物的重力為490 N，ANSYS仿真結果在表6中，ANSYS仿真結果與懸鏈線計算的結果比較見表7。

圖7 索道模擬單元劃分示意Fig.7 The simulation of ropeway

有限元仿真結果在表6中，有限元仿真結果與懸鏈線計算的結果比較見表7。

表6 索道的有限元計算結果

表7 索道的理論結果和仿真結果對比

Table 7 The comparison between theoretical and simulation results

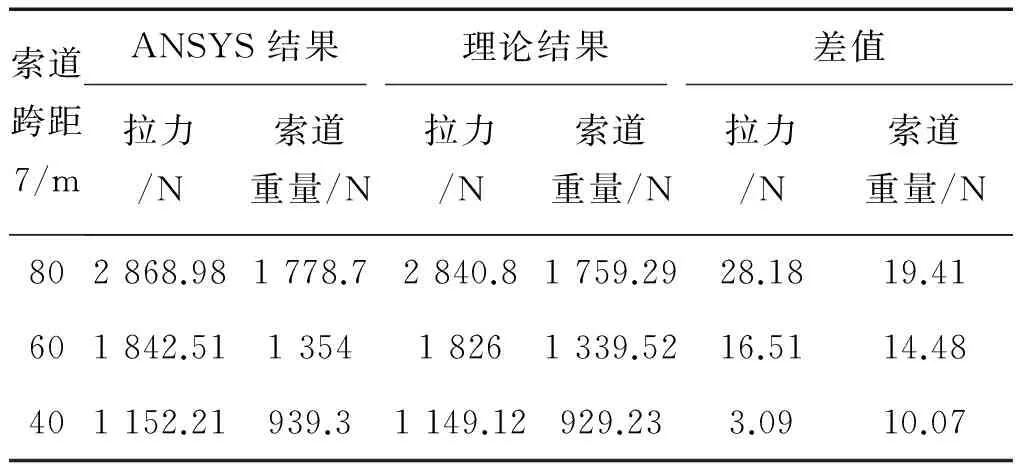
索道跨距7/mANSYS結果理論結果差值拉力/N索道重量/N拉力/N索道重量/N拉力/N索道重量/N802868.981778.72840.81759.2928.1819.41601842.51135418261339.5216.5114.48401152.21939.31149.12929.233.0910.07

圖8 理論與仿真得到索道拉力差值隨跨距變化Fig.8 The ropeway tension difference between theoretical results and simulation results in different ropeway spans

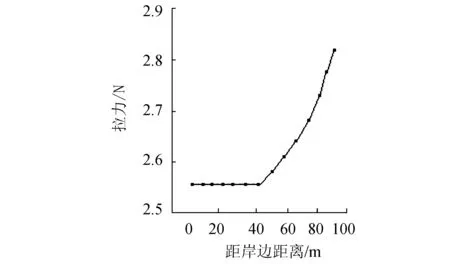
圖9 牽引拉力隨離岸距離變化關系(索道跨距80 m)Fig.9 The ropeway tension in different ropeway spans. (The ropeway span is 80 m)

從表7和圖8來看，仿真結果和理論結果整體吻合，隨著跨距的增加，拉力差值在增大，在跨距為80 m時，拉力差值為28 N，與拉力的比值約為1%，理論分析值相對仿真結果值偏小，表明理論模型簡化因素較多，隨著跨距增加，索道跨距80 m之后，應以仿真分析模型為主。

從圖9來看，在索道跨距80 m時，在船上牽引岸上的索具過程中，牽引拉力隨距岸距離是變化的，牽引拉力在40 m的范圍內變化不大，超越這一范圍后，隨著距離的增加呈線性增加，也會越來越費力。

3 結論

本文主要分析了船只補給懸鏈線系統的運動特性，并考慮了船只與錨泊系統的耦合以及船只運動對索道的影響，通過理論分析和仿真模擬，得到了船只懸鏈線系統連接動力學響應，并對結果進行了分析，得到以下結論：

1)通過對船只與懸鏈線運動分析，得到了系統連接的運動特性，為船只懸鏈線系統設計提供理論依據。

2)三級海況下，對船只和固定物連接影響較大的因素為縱蕩和縱搖，在連接設備時應將船只側面對著固定物，連接點應在船只的中心線上，降低縱蕩，縱搖對索道的影響。

3)垂蕩會引起連接點位置的變化，在三級海況下垂蕩的最大值為0.15 m，對連接點位置影響較小，可忽略其影響，在高海況條件下，應考慮該因素。

4)考慮了錨泊系統耦合運動后，船只的運動較為復雜，在做周期運動的同時，也會做小范圍運動，對船只和固定物連接影響較小，但應注意防止走錨現象的發生。

5)仿真結果和理論結果基本保持一致，隨著跨距的增加，拉力差值在增大，跨距小于80 m時，拉力差值與拉力的比值為1%；理論分析值相對仿真結果值偏小，表明理論模型簡化因素較多，隨著跨距增加，索道跨距80 m之后，應以仿真分析模型為主。

6)在索道跨距80 m時，在船上牽引岸上的索具過程中，牽引拉力隨距岸距離是變化的，牽引拉力在40 m的范圍內變化不大，超越這一范圍后，隨著距離的增加呈線性增加，也會越來越費力。

[1]CHEN S, MAHRENHOLTZ O. Interaction of water waves and floating twin cylinders in beam waves[J]. Applied ocean research, 1994, 14(6): 371-379.

[2]MCTAGGART K, CUMMING D, HSIUNG C C, et al. Seakeeping of two ships in close proximity[J]. Ocean engineering, 2003, 30(8): 1051-1063.

[3]FANG M C, KIM C H. An analysis of water shipping between two floating platforms in the beam wave[C]//Proceedings of the Fifth International Symposium on Offshore Mechanics and Arctic Engineering. Tokyo, 1986, 1: 499-505.

[4]DUNCAN J H, BARR R A, LIU Y Z. Computations of the coupled response of two bodies in a seaway[C]//International Workshop on Ship and Platform Motions. Berkeley, CA, 1983.

[5]VAN OORTMERSSEN G. Hydrodynamic interaction between two structures floating in waves[C]//Proceedings of 2nd International Conference on Behaviour of Off-shore Structures. London, 1979: 339-356.

[6]CHEN S, MAHRENHOLTZ O. Interaction of water waves and floating twin cylinders in beam waves[J]. Applied ocean research, 1992, 14(6): 371-379.

[7]NEWMAN J N. Wave effects on deformable bodies[J]. Applied ocean research, 1994, 16(1): 47-59.

[8]沈慶, 陳徐均. 系泊多浮體系統波浪運動響應的動力學分析[J]. 解放軍理工大學學報, 2002, 1(4): 31-36. SHEN Qing, CHEN Xujun. Dynamic analysis of moored multi-body floating system’s responses to regular waves[J]. Journal of PLA university of science and technology, 2002, 1(4): 31-36.

[9]勾瑩, 滕斌, 寧德志. 波浪與兩相連浮體的相互作用[J]. 中國工程科學, 2004, 6(7): 75-80, 93. GOU Ying, TENG Bin, NING Dezhi. Interaction effects between wave and two connected floating bodies[J]. Engineering science, 2004, 6(7): 75-80, 93.

[10]HONG S Y, KIM J H, CHO S K, et al. Numerical and experimental study on hydrodynamic interaction of side-by-side moored multiple vessels[J]. Ocean engineering, 2005, 32(7): 783-801.

[11]SUN L, TAYLOR R E, CHOO Y S. Responses of interconnected floating bodies[J]. The IES journal part a: civil & structural engineering, 2011: 4(3): 143-156.

[12]劉文璽, 周其斗, 張緯康, 等. 浮體與系泊系統的耦合動力分析[J]. 船舶力學, 2014, 18(8): 940-957. LIU Wenxi, ZHOU Qidou, ZHANG Weikang, et al. Dynamic analysis of the coupled floating body/mooring system[J]. Journal of ship mechanics, 2014, 18(8): 940-957.

[13]許鑫, 楊建民, 李欣, 等. 海洋工程中多浮體系統的水動力研究綜述[J]. 中國海洋平臺, 2014, 29(4): 1-8, 13. XU Xin, YANG Jianmin, LI Xin, et al. Review of the research on multi-body system hydrodynamics[J]. China offshore platform, 2014, 29(4): 1-8, 13.

[14]張立忠. 我國礦山載人索道現狀及發展前景[J]. 中國索道, 2002, 2(5): 1-4. ZHANG Lizhong. Development and application of carrying people ropeway in the mine[J]. China ropeway, 2002, 2(5): 1-4.

[15]任愛娣, 張得偉, 何學軍. 航行橫向補給艦船運動對高架索張力影響[J]. 艦船科學技術, 2014, 36(7): 94-96, 102. REN Aidi, ZHANG Dewei, HE Xuejun. Influence of tension in highline cable of alongside replenishment by the motion of ships[J]. Ship science and technology, 2014, 36(7): 94-96, 102.

[16]余建星, 顧鵬. 海上干貨補給技術[J]. 海洋技術, 2005, 24(3): 105-110. YU Jianxing, GU Peng. The technique of solid cargo supplying on the sea[J]. Ocean technology, 2005, 24(3): 105-110.

[17]鄭麗鳳, 周新年, 巫志龍. 懸索的理論計算與實測誤差分析[J]. 北華大學學報: 自然科學版, 2010, 11(2): 162-168. ZHENG Lifeng, ZHOU Xinnian, WU Zhilong. Error analysis among theoretical calculation and measure data of flexible cable[J]. Journal of Beihua university: natural science, 2010, 11(2): 162-168.

[18]周新年. 架空索道理論與實踐[M]. 北京: 中國林業出版社, 1996: 140-200. ZHOU Xinnian. Theory and practice of aerial ropeway[M]. Beijing: China Forestry Publishing House, 1996: 140-200.

[19]余建星, 顧鵬. 海上分離式輕型補給系統研究[J]. 天津大學學報, 2006, 39(11): 1270-1271. YU Jianxing, GU Peng. Offshore minitype detached replenishment system[J]. Journal of Tianjin university, 2006, 39(11): 1270-1271.

Analysis of motion characteristics of supply vessel catenary systems

WU Weiguo1,2，TAN Zhendong3，WANG Zhentao2，LENG Yonggang1，DU Zunfeng4

(1.School of Mechanical Engineering, Tianjin University, Tianjin 300072, China; 2.Military Transportation Institute, Tianjin 300161, China; 3.Tianjin Science and Technology Commission, Tianjin 300051, China; 4.State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China)

The cableway has been widely used by supply vessels in shore-to-ship or ship-to-ship transfers of goods and materials. By analyzing the motion of the catenary system in supply vessels, and considering the effects of the coupling of vessels and mooring systems and the shipmotion on cableways, we calculated the dynamic response of the catenary systems of supply vessels, from which obtained the motion characteristics of vessel catenary systems. The result provides the basis for the cableway design. Based on the cableway catenary theory and using the finite element method (FEM), we established a model and performed simulations. We then compared the numerical simulation and theoretical results, which showed that the results were mostly consistent. In a sea state code of 3, vessels should be connected to the device side facing the fixture and the connection point should be on the centerline of the vessel. In a very rough ocean environment, the impact of heave should be considered. As there are many simplified factors in the theoretical model, when the cableway span exceeds 80 m, the simulation model should be considered first.

vessel supply; catenary system; motion characteristics; dynamic response; FEM

2015-09-14.

時間：2016-12-21.

國家自然科學基金項目(51109158)；天津市應用基礎與前沿技術研究計劃(15JCZDJC32200).

吳衛國(1983-), 男, 博士； 冷永剛(1964-), 男, 教授，博士生導師.

冷永剛，E-mail：leng_yg@tju.edu.cn.

10.11990/jheu.201509045

U644

A

1006-7043(2017)01-126-07

吳衛國,譚振東,王振濤,等. 船只補給懸鏈線系統運動特性分析[J]. 哈爾濱工程大學學報， 2017, 38(1): 126-132. WU Weiguo，TAN Zhendong，WANG Zhentao,et al. Analysis of motion characteristics of supply vessel catenary systems[J]. Journal of Harbin Engineering University, 2017, 38(1): 126-132.

網絡出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20161221.1524.002.html