一種無證書盲簽名方案的分析與改進
劉二根 王 霞 周華靜
(華東交通大學理學院 江西 南昌 330013) (華東交通大學系統工程與密碼學研究所 江西 南昌 330013)
一種無證書盲簽名方案的分析與改進
劉二根 王 霞*周華靜
(華東交通大學理學院 江西 南昌 330013) (華東交通大學系統工程與密碼學研究所 江西 南昌 330013)
通過對黃茹芬等提出的無證書盲簽名方案進行安全性分析,發現該方案存在公鑰替換攻擊的漏洞。針對該問題,提出一個能夠抵抗公鑰替換這一攻擊的無證書盲簽名方案,而且最終證明了改進的方案在隨機預言機模型和inv-CDH困難問題假設下對于適應性選擇消息攻擊是存在性不可偽造的。
盲簽名 不可偽造性 隨機預言機模型 盲性
0 引 言
1982年,Chaum[1]首先提出了盲簽名這一概念。所謂盲簽名,即是簽名者雖然對消息簽了名,但對他所簽消息的內容是 未知的。正是由于這一特點,使得盲簽名在電子支付和電子投票中得到廣泛的應用。為了解決傳統公鑰密碼體制中公鑰證書的存儲和管理問題,基于身份的密碼體制被Shamir等[2]提出。在基于身份的密碼體制中存在密鑰托管這一問題,因為由可信中心KGC生成用戶私鑰。2003年,無證書公鑰密碼體制由Al-Riyami等[3]提出,也相繼出現了許多簽名和加密方案[4-6]。在無證書密碼體制中,密鑰生成中心只產生用戶的部分私鑰,但卻無法知道長期私鑰,解決了該體制中的密鑰托管這一問題。將盲簽名與無證書公鑰密碼體制相結合可以產生無證書盲簽名,由此許多無證書盲簽名方案[7-13]應運而生。2012年,黃茹芬等[14]提出了一個基于inv-CDH問題和q-SDH問題的無證書盲簽名方案,但通過分析發現其存在公鑰替換攻擊這一漏洞。本文提出了一個改進的方案,新方案不僅具有盲性,而且證明了在隨機預言機模型下是存在性不可偽造的。
1 預備知識
1.1 雙線性映射
設G1、G2分別是由P生成的p階加法群和乘法群,e:G1×G1→G2是滿足下面3個性質的雙線性映射:
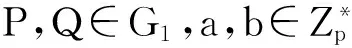
(2) 非退化性:有P,Q∈G1,使得e(P,Q)≠1;
(3) 可計算性:?P,Q∈G1,能夠計算出e(P,Q)。
1.2 逆計算Diffie-Hellman困難(inv-CDH)問題
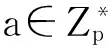
1.3 惡意攻擊者模型
在無證書簽名方案中,有2種類型的攻擊者:
(1) 類型1的攻擊者M1:無法知道系統主密鑰,但可以替換用戶公鑰;
(2) 類型2的攻擊者M2:能夠知道系統主密鑰,但不能替換用戶的公鑰。
2 文獻[14]方案的分析
2.1 方案回顧
文獻[14]方案包括下面7個具體算法:
1) 初始化
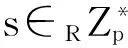
2) 生成部分私鑰

3) 秘密值生成
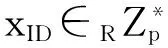
4) 私鑰生成
輸入A的部分私鑰DID和秘密值xID,A產生自己的私鑰SKID=(xID,DID)。
5) 公鑰生成
輸入系統公開參數params、秘密值xID和部分私鑰DID,輸出A的公鑰PKID=xID(Ppub+QIDP)。
6) 簽名過程
輸入系統公開參數params、消息m、A的身份ID和私鑰SKID,具體如下:
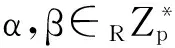

(4) 解盲:B得到S=β-1S′,關于消息m的盲簽名為σ=(S,h)。
7) 驗證
對于給定的消息簽名對(m,S,h)、簽名者身份ID和公鑰PKID,驗證等式h=H2(m,e(S,PKID)g-h)是不是成立,若成立則接受,不成立則拒絕。
2.2 攻擊方法

=H2(m,e(k-1S,kxID(Ppub+QIDP))g-h)
=H2(m,e(β-1(r+βh+α)P,P)g-h)
=H2(m,(Ugα)β-1)=H2(m,V)
那么,σ*=(S*,h)是一個有效的盲簽名。
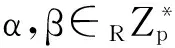
4) 解盲:B計算S*=β-1S′,消息m的盲簽名為σ=(S*,h)。
事實上,σ*=(S*,h)是一個有效的盲簽名。因為:
=H2(m,e(β-1S′,ωP-H1(ID)P)g-h)
=H2(m,e(β-1(r+βh+α)P,P)g-h)
=H2(m,(Ugα)β-1)=H2(m,V)
從以上的攻擊方法得知,原方案之所以存在公鑰替換攻擊,是因為沒有將用戶公鑰綁定到部分私鑰上。如果用戶公鑰通過哈希函數綁定到部分私鑰中,部分私鑰DID是不可偽造的,則不存在公鑰替換攻擊。
3 文獻[14]方案的改進
只需要修改文獻[14]方案的部分私鑰生成算法、公鑰生成算法、簽名過程和驗證算法,其他三個算法保持不變。
1) 公鑰生成
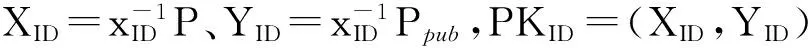
2) 部分私鑰生成
3) 簽名
承諾、盲化和解盲與原方案相同,只需修改簽名這一步。
簽名:簽名者計算S′=(r+h′)xIDDID,把S′發給用戶。
4) 驗證
給定消息簽名對(m,S,h)、簽名者身份ID和公鑰PKID=(XID,YID),驗證等式h=H2(m,e(S,XID+QIDYID)g-h)是不是成立,若成立則接受,否則拒絕。
4 安全性分析與效率分析
4.1 方案的正確性
定理1 改進的無證書盲簽名方案是正確的。
證明:
h=H2(m,e(S,XID+QIDYID)g-h)
=H2(m,e(β-1(r+h′)xIDDID,XID+QIDYID)g-h)
=H2(m,e(β-1(r+βh+α)P,P)g-h)
=H2(m,(Ugα)β-1)=H2(m,V)
4.2 具有盲性
定理2 新方案具有盲性。
證明:給一個正確的消息簽名對(m,S,h)和任意一組盲簽名發布過程中產生的視圖(U,h′,S′),考慮下列等式:
S=β-1S′
(1)
h′=βh+αmodp
(2)
4.3 安全性分析
定理3 改進的無證書盲簽名方案不存在公鑰替換攻擊。
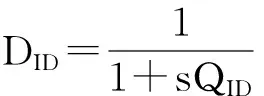
由于類型2的攻擊更有破壞力,如果攻擊成功其影響將是任何用戶。本文只證明對類型2攻擊下是可證安全的,類型1的證明過程相似(只是詢問過程有些不同)。
定理4 在隨機預言機模型和inv-CDH困難問題假設下,新方案對攻擊者M2在適應性選擇消息攻擊條件下是存在性不可偽造的。
證明:假設M2能以不可忽略的優勢成功攻擊該新方案,構造一個在概率多項式時間內能夠解決inv-CDH問題的算法B。
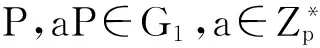
1) 系統設置:算法B生成系統公開參數params={G1,G2,e,q,P,g,H1,H2},并發送系統公開參數和主密鑰s給攻擊者M2,系統公鑰設置為Ppub=sP。列表L1、L2、LP、LPK、LSK、LS分別用于應對M2對預言機的H1詢問、H2詢問、部分密鑰詢問、公鑰詢問、私鑰詢問、簽名詢問。B通過維護表L1來響應M2的H1詢問(M2至多可以做qH1次H1詢問),表L1的表結構為(IDi,Xi,Yi,h1i)。B通過維護表L2來響應M2的H2詢問(M2至多可以做qH2次H2詢問),表L2的表結構為(m,V,h2i)。B通過維護表LP來響應M2的部分密鑰詢問(M2至多可以做qp次部分密鑰詢問),表LP的表結構為(IDi,DIDi)。B通過維護表LSK來響應M2的私鑰詢問(M2至多可以做qsk次私鑰詢問),表LSK的表結構為(IDi,xIDi,DIDi)。B通過維護表LPK來響應M2的公鑰詢問(M2至多可以做qpk次公鑰詢問),表LPK的表結構為(IDi,xIDi,XIDi,YIDi)。B通過維護列表LS來響應M2關于(m,IDi)的簽名詢問(M2至多可以做qs次簽名詢問),表LS的表結構為(m,IDi,S,h2i)。初始化所有表為空。假設攻擊者M2攻擊的目標ID為ID*,那么不能詢問身份ID*的長期私鑰,用a-1來模擬ID*的長期私鑰,對應的公鑰為XID*=aP、YID*=aPpub。
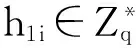
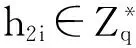
4) 公鑰詢問:當B收到關于IDi的公鑰詢問時:
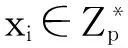
(2) 如果IDi=ID*,用a-1來模擬ID*的長期私鑰,公鑰XID*=aP、YID*=aPpub,將(ID*,⊥,XID*,YID*)添加到表LPK中并返回(XID*,YID*)給M2。
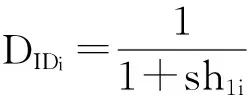
6) 私鑰詢問:當B收到關于IDi的私鑰詢問時:
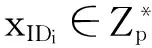
(2) 如果IDi=ID*,算法終止。
7) 簽名詢問:當B收到關于(m,IDi)的簽名詢問時:
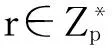
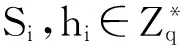
若算法B沒有停止,那么M2在沒有詢問ID*的私鑰和(ID*,m*)的簽名的情況下,能夠以一個不可忽略的概率對消息m*輸出一個有效的簽名σ=(S,h)。根據分叉引理,對M2哈希重放,B可以得到關于m*的兩個有效(ID*,m*,S,h)和(ID*,m*,S′,h′),h≠h′。有效的簽名滿足:e(S,XID*+h*YID*)g-h=V,e(S′,XID*+h*YID*)g-h′=V,其中h*=H1(ID*)。于是有:e(S,XID*+h*YID*)g-h=e(S′,XID*+h*YID*)g-h′。由h≠h′,可以得到:a-1P=(S-S′)(1+h*s)(h-h′)-1。
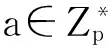
5 性能分析
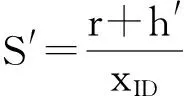
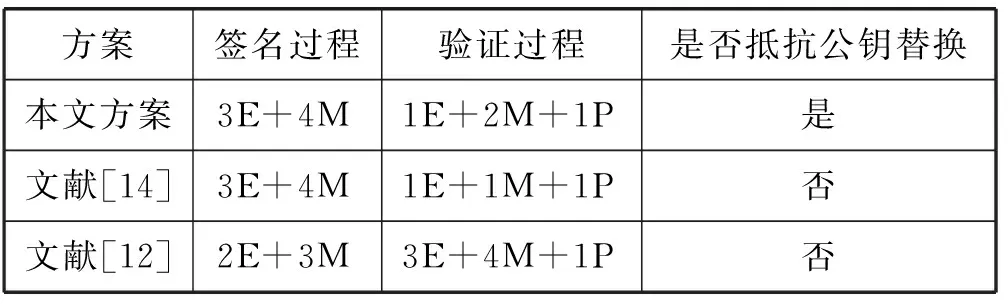
表1 本方案與其他方案的性能比較
6 結 語
通過對黃茹芬等提出的無證書盲簽名方案進行安全性分析,發現該方案不能抵抗公鑰替換攻擊。由此提出了一個改進的無證書盲簽名方案,將簽名者的公鑰綁定到部分私鑰中,有效地解決了原方案中存在的公鑰替換攻擊的問題,并證明了在隨機預言機模型和inv-CDH困難問題假設下對于適應性選擇消息攻擊是存在性不可偽造的。同時該方案是基于無證書密碼體制的,克服了證書管理和密鑰托管問題。
[1]ChaumD.Blindsignaturesforuntraceablepayments[C]//AdvancesinCryptology:ProceedingsofCrypto’82,1983:199-203.
[2]ShamirA.Identity-basedcryptosystemsandsignaturesschemes[C]//ProceedingsofCrypto’84onAdvancesinCryptology.NewYork:Springer-Verlag,1985:47-53.
[3]Al-RiyamiSS,PatersonKG.Certificatelesspublickeycryptography[C]//Proceedingsofthe9thInternationalConferenceontheTheoryandApplicationofCryptologyandInformationSecurity,2003:452-473.
[4]ChoiKY,ParkJH,HwangJY,etal.Efficientcertificatelesssignatureschemes[C]//Proceedingsofthe5thInternationalConferenceonAppliedCryptographyandNetworkSecurity,2007:443-458.
[5] 王圣寶,劉文浩,謝琪.無雙線性配對的無證書簽名方案[J].通信學報,2012,33(4):93-98.
[6]ZhangL,ZhangF.Certificatelesssignatureandblindsignature[J].JournalofElectronics(China),2008,25(5):629-635.
[7] 魏萍,陳海濱,楊曉元.一個安全無證書的盲簽名方案[J].計算機工程與應用,2011,47(5):96-97.
[8] 楊曉元,梁中銀,郭耀,等.一個高效的無證書盲簽名方案[J].南京郵電大學學報(自然科學版),2009,29(3):37-42.
[9] 周才學.三個無證書簽名方案的密碼學分析與改進[J].計算機工程,2012,38(19):114-118.
[10] 張玉磊,王彩芬,張永潔,等.基于雙線性對的高效無證書簽名方案[J].計算機應用,2009,29(5):1330-1333.
[11] 文佳駿,左黎明,李彪.一個高效的無證書代理盲簽名方案[J].計算機工程與科學,2014,36(3):452-457.
[12] 梁紅梅,黃振杰.高效無證書簽名方案的安全性分析和改進[J].計算機應用,2010,30(3):685-687,698.
[13] 何俊杰,王娟,祁傳達.對一個無證書盲簽名方案的攻擊與改進[J].數學的實踐與認識,2014,44(4):123-128.
[14] 黃茹芬,農強,黃振杰.一個高效的無證書盲簽名方案[J].計算機工程,2013,39(2):130-136.
ANALYSIS AND IMPROVEMENT OF A CERTIFICATELESS BLIND SIGNATURE SCHEME
Liu Ergen Wang Xia*Zhou Huajing
(SchoolofScience,EastChinaJiaotongUniversity,Nanchang330013,Jiangxi,China) (InstituteofSystemEngineeringandCryptography,EastChinaJiaotongUniversity,Nanchang330013,Jiangxi,China)
After analyzing the security of the blind signature scheme without certificates proposed by Huang Rufen et al, it is found that the scheme cannot resist public key replaced attack. Thus, a modified certificateless blind signature scheme which can resist public key attack is proposed, and the scheme is finally proved to be existentially unforgeable against adaptive chosen message in random oracle model and under inv-CDH complexity assumption.
Blind signature Unforgeability Random oracle model Blindness
2015-09-05。國家自然科學基金項目(11361024,11261019,61472138,61263032)。劉二根,教授,主研領域:圖論及其優化。王霞,碩士生。周華靜,碩士生。
TP309
A
10.3969/j.issn.1000-386x.2017.02.056

