基于MC-FEM方法的再生混凝土有效彈性模量分析★

王 辰 吳宇清*

(同濟大學，上海 200092)

基于MC-FEM方法的再生混凝土有效彈性模量分析★

王 辰 吳宇清*

(同濟大學，上海 200092)

結合有限單元法和Monte-Carlo法，利用均質化理論，從隨機骨料代表體元中計算得到再生混凝土有效彈性模量的概率分布，數值試驗結果顯示，不同級配的再生混凝土等效彈性模量分布有著明顯的變化趨勢，且近似服從對數正態分布。

再生混凝土，漸進均質化，Monte-Carlo法

0 引言

再生混凝土能夠緩解天然砂石骨料的匱乏，減少廢棄混凝土填埋對環境造成的污染，是一種新興的可持續建筑材料[1]。彈性模量是混凝土材料最為基本和重要的力學指標之一，是計算結構變形、溫度應力和裂縫開展等問題的必要參數。目前，對再生混凝土彈性模量的研究仍以試驗為主[2-4]。試驗手段簡單直接，但是會耗費大量資金和時間，且經常帶有較強的主觀意向，難以為再生混凝土表現出的離散性提供理論上的解釋和大量數據的支撐。隨著計算機技術的快速發展，數值模擬成為分析混凝土材料細觀力學性能的重要手段。肖建莊等[5]對模型再生混凝土進行了單軸受壓模擬，在此基礎上李文貴等[6]對受壓應力分布特征進行了討論。

本文建立了不同級配的骨料隨機分布模型，運用漸進均質化理論和Monte-Carlo法，對多種級配、再生骨料取代率的再生混凝土代表體元進行大量有限元計算。最終，對不同情況下的有效彈性模量大小和離散性進行了討論，并根據有效彈性模量的統計特征進行了概率分布擬合。

1 均質化理論

均質化理論是一套嚴格的數學理論，該方法是由Beran[7]和Hashin與Shtrikman[8]最先提出，并在之后得到了進一步的發展。其中，漸進均質化方法被廣泛應用，下面介紹漸進均質化方法。

復合材料粗細尺度上的彈性系數可以定義為：

(1)

其中，x為粗尺度坐標；y為細尺度坐標，兩者關系為y=x/β，β為大于0且遠小于1的數，用來描述粗細尺度之間的倍數關系。

彈性力學問題中平衡方程可以寫為:

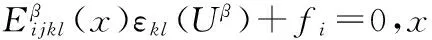
(2)

邊界條件給定為:

ε11(x?Ω)=1

(3)

其中，ε11為細尺度上的應變；fi為體力。

(4)

定義線性形式如下:

L(η)=∫ΩfiηidΩ+∫Ωσiηid(?Ω)

(5)

由虛位移原理:

(6)

這里我們引入均質化函數χ(ij)k，χ(ij)k滿足下式:

aβ((χ(ij)k+yjδki)nk,fT)=0

(7)

其中,fT為任意周期函數;δki為Kronecker符號;nk為單位坐標向量。

對于任意的容許位移V有:

D(U,V)=∫Ωεkl(U)Dijklεij(V)dΩ

(8)

其中:

(9)

由以上兩式可以得到彈性系數的均質化表達式為:

從長遠角度來看，預算法的深度實施有利于事業單位財務管理水平規范程度以及總體水平的提升。現階段，雖然，很多事業單位對預算法的適應性較強，但財務管理活動開展中也暴露出了很多問題。事業單位需要對自身財務管理上存在的不足予以正視，并在充分研讀預算法中財務管理與預算管理相關內容的基礎上，不斷對財務管理中遇到的問題進行解決并促進財務管理水平的持續提升。

(10)

通過設定均質化邊界條件結合以上各式就可以求得有效彈性模量。

2 隨機骨料模型的參數設置

代表體元選用正方形，邊長為100mm。為簡化分析，骨料可取為圓形，忽略界面過渡區影響。骨料粒徑取為5mm～20mm。

參考相關文獻[5][6]，取定天然骨料彈性模量為50 GPa，泊松比為0.16；老砂漿彈性模量為25 GPa，泊松比為0.22；新砂漿為30 MPa，泊松比為0.22。隨機骨料模型考慮了骨料分布的隨機性、骨料粒徑大小的隨機性，可根據不同級配來生成不同的隨機樣本。

3 數值試驗及結果

3.1 試驗結果的討論

設置MC抽樣次數為500，計算了粒徑為5 mm，20 mm的單一級配代表體元以及連續級配代表體元。數值模擬結果如圖1，圖2所示，可以看到蒙特卡洛樣本的均值和變異系數收斂效果明顯。小粒徑級配有效彈性模量均值要大于大粒徑級配，而連續級配則介于兩者之間；小粒徑級配有效彈性模量變異系數小于大粒徑級配，連續級配則均大于前兩者。連續級配更具離散性。

3.2 有效彈性模量概率分布擬合

對不同級配再生混凝土代表體元的有效彈性模量樣本進行對數正態分布擬合。表征擬合效果的可決系數R2調整值如表1所示。可決系數R2調整值是一個0～1之間的非負值，值越大說明擬合優度越好。

不同替代率R2調整值均在0.9以上，擬合優度佳，可以認為連續級配再生混凝土代表體元有效彈性模量樣本用對數正態分布近似表征。

表1 對數正態分布擬合的R2調整值

4 結語

本文得出的主要結論如下：

1)再生混凝土骨料體積分數與取代率一定時，小粒徑單一級配有效彈性模量均值要高于大粒徑單一級配，連續級配介于兩者之間。小粒徑單一級配有效彈性模量變異系數要小于大粒徑單一級配，連續級配均高于前兩者。

2)對數正態分布對級配的再生混凝土隨機骨料代表體元有效彈性模量擬合良好，可認為隨機骨料再生混凝土代表體元有效彈性模量服從對數正態分布。

通過MC-FEM對再生混凝土隨機骨料模型進行彈性均質化分析，可以得到其有效彈性模量的分布，為再生混凝土細觀分析引入了隨機性，與常規模型相比更加合理。

[1] 肖建莊.再生混凝土[M].北京：中國建筑工業出版社,2008.

[2] 陳宗平,徐金俊,鄭華海,等.再生混凝土基本力學性能試驗及應力應變本構關系[J].建筑材料學報,2013,16(1):24-32.

[3] Xiao J, Li J, Zhang C. Mechanical properties of recycled aggregate concrete under uniaxial loading[J].Cement & Concrete Research,2005,35(6):1187-1194.

[4] 肖建莊.再生混凝土單軸受壓應力—應變全曲線試驗研究[J].同濟大學學報(自然科學版),2007,35(11):1445-1449.

[5] 肖建莊,李文貴,劉 瓊,等.模型再生混凝土單軸受壓性能細觀數值模擬[J].同濟大學學報(自然科學版),2011,39(6):791-797.

[6] 李文貴,肖建莊,袁俊強,等.模型再生混凝土單軸受壓應力分布特征[J].同濟大學學報(自然科學版),2012,40(6):906-913.

[7] Beran MJ.Statistical Continuum Theories,Monographs in Statistical Physics and Thermodynamics. Wiley: New York,1968.

[8] Hashin Z, Shtrikman S. A variational approach to the theory of the elastic behaviour of multiphase materials. Journal of Mechanics Physics and Solids，1963(11):127-140.

[9] Hill R. The Elastic Behaviour of a Crystalline Aggregate[J].Proceedings of the Physical Society,1952,65(5):349-354.

[10] Kamiński M,Kleiber M.Perturbation based stochastic finite element method for homogenization of two-phase elastic composites[J].Computers & Structures,2000,78(6):811-826.

[11] Walraven J C.Aggregate interlock:A theoretical and experimental analysis[D].Delft University Press,1980.

Effective elastic modulus analysis of recycled concrete on the basis of MC-FEM method★

Wang Chen Wu Yuqing*

(TongjiUniversity,Shanghai200092,China)

Combining with finite element method and Monte-Carlo method, applying homogenization theory, the article achieves effective elastic modulus probability distribution of recycled concrete from random aggregate. The numerical test results show that: equivalent elastic modulus distribution of recycled concrete with different grading will have obvious change trend.

recycled concrete, gradual homogenization, Monte-Carlo method

1009-6825(2017)02-0115-02

2016-11-01★:國家自然科學基金項目(項目編號：10972162)

王 辰(1992- )，男，在讀碩士

吳宇清

TU528

A