多種方法求體積

◎曾榮

多種方法求體積

◎曾榮

數(shù)學課上，老師出了這樣一道題(如下圖)：一個機器零件，上面是圓錐形，高12厘米，下面是圓柱形，底面直徑是8厘米，高是12厘米。求這個機器零件的體積是多少立方厘米？

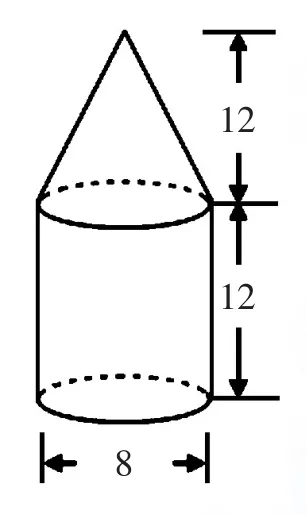
李俊說：“圓柱的體積是3.14×(8÷2)2×12=602.88(立方厘米)，圓錐的體積是：602.88×=200.96(立方厘米)，所以，這個機器的零件是602.88+200.96=803.84(立方厘米)。”

謝平說：“假設(shè)把圓錐部分轉(zhuǎn)化成與其底面積相同的圓柱，這個圓柱的高就是圓錐的，整個零件的體積就相當于一個高為12+12÷3=16(厘米)的圓柱體積。即這個機器零件的體積是：3.14×(8÷2)2×16=803.84(立方厘米)。”

張華說：“由于圓錐與圓柱等底等高，因此圓錐部分的體積相當于圓柱的，那么整個零件的體積就是圓柱體積的1+=倍，即這個機器零件的體積是：3.14×(8÷2)2×12×=803.84(立方厘米)。”

聽了同學們的解答，老師高興地說：“上面三種解法都對，我們在解決問題時，如果能從不同的角度去分析、思考，不僅有利于開闊解題思路，還能把學過的知識融會貫通。”