面向動力鋰電池內(nèi)部視電阻率三維反演成像方法
謝爍熳,許維鎣,洪曉斌
(華南理工大學機械與汽車工程學院,廣東 廣州 510640)
面向動力鋰電池內(nèi)部視電阻率三維反演成像方法
謝爍熳,許維鎣,洪曉斌
(華南理工大學機械與汽車工程學院,廣東 廣州 510640)
為滿足電阻層析成像方法應用于動力鋰電池內(nèi)部結(jié)構(gòu)狀態(tài)監(jiān)測的精度與實時性要求,提出一種三維電阻層析成像反演算法。針對高斯-牛頓算法的特點,對標準高斯-牛頓算法施加光滑約束,使迭代步長在保證收斂的情況下達到最優(yōu)化。根據(jù)動力鋰電池內(nèi)部視電阻率三維反演成像實驗獲得的測量結(jié)果,研究常規(guī)高斯-牛頓算法和光滑約束高斯-牛頓算法的反演能力。結(jié)果表明:光滑約束高斯-牛頓算法收斂快,提高了檢測效率,能夠反映動力鋰電池內(nèi)部的視電阻率變化趨勢,并對動力鋰電池內(nèi)部的視電阻率分布做出有效評估。
視電阻率;三維圖像反演;高斯-牛頓算法;動力鋰電池
0 引 言
動力鋰電池是理想的儲能元件,得到社會各界的高度關(guān)注,其測試與評估已經(jīng)成為研究熱點。動力鋰電池的測試與評估主要包括壽命評估、安全性能評估等,其中對于安全性能的測試與評估被廣泛開展,例如,Oh S H等[1]研究了循環(huán)應用下正極材料與電池安全性能的關(guān)系;McCleary等[2]通過建立模型探索了環(huán)境溫度對鋰離子電池安全性的影響;于申軍等[3]研究了內(nèi)阻差異對不同連接方式動力鋰電池組安全性能的影響。然而,對于動力鋰電池由內(nèi)部結(jié)構(gòu)變化引發(fā)的安全隱患的篩查尚未適應其安全性能評估的要求。
電阻層析成像技術(shù)能夠利用相應的圖像重建算法,非侵入性地重建被測物場的介質(zhì)分布圖,獲取物體截面相分布的微觀信息,在地質(zhì)勘查、石油化工、冶金等國民經(jīng)濟行業(yè)中有著廣泛的應用前景。其中,作為該技術(shù)主要參數(shù)指標的電導率/電阻率能夠完整反映被測物場的介質(zhì)構(gòu)成,進而能夠?qū)Ρ粶y對象的內(nèi)部狀態(tài)進行狀態(tài)評估。電阻率與動力電池內(nèi)部構(gòu)成的物理化學特性密切相關(guān)[4],物理化學特性發(fā)生變化時視電阻率分布相應呈現(xiàn)出變化。通過實時監(jiān)測動力電池內(nèi)部視電阻率變化可以對電池在不同使用環(huán)境、不同使用條件下的失效進行分析。
圖像反演算法的精度和速度是電阻層析成像技術(shù)成功應用的關(guān)鍵之一,各國學者基于各種圖像反演算法做了大量研究工作。目前,二維圖像反演技術(shù)已經(jīng)發(fā)展成熟,但其成像目標局限于一系列的二維截面,忽略檢測目標幾何形狀、空間分布等三維信息。因此,發(fā)展三維圖像反演技術(shù)十分必要。三維圖像反演研究起步于國外,主要包括數(shù)據(jù)采集、成像模型、成像算法等方面,例如,Nick等[5]開發(fā)了基于EIT的光學材料性能邊界測試三維可視化工具包;Zhdanov等[6]建立了基于電磁鉆孔測量的井間三維電磁成像模型;Doetsch等[7]利用延時三維表面ERT獲知地下水系統(tǒng)狀況。目前國內(nèi)研究主要包括三維圖像正演仿真及三維圖像反演算法等,徐光捷等[8]采用有限元數(shù)值仿真建立三維模型獲得ERT傳感器敏感場的三維空間分布,分析場域分布的不均勻性;針對ERT成像分辨率低的問題,李守曉等[9]提出基于三維模型的改進Tikhonov迭代電阻成像算法。對于基于ERT技術(shù)的三維圖像反演,尤其是復雜的動力鋰電池內(nèi)部結(jié)構(gòu)的三維圖像反演,目前國內(nèi)仍很少涉及。本文在前期的采用電阻層析成像技術(shù)結(jié)合電性能監(jiān)測電池內(nèi)部狀態(tài)的基礎(chǔ)上[10],提出通過三維圖像反演算法對視電阻率進行成像,快速判斷電池內(nèi)部狀態(tài)。
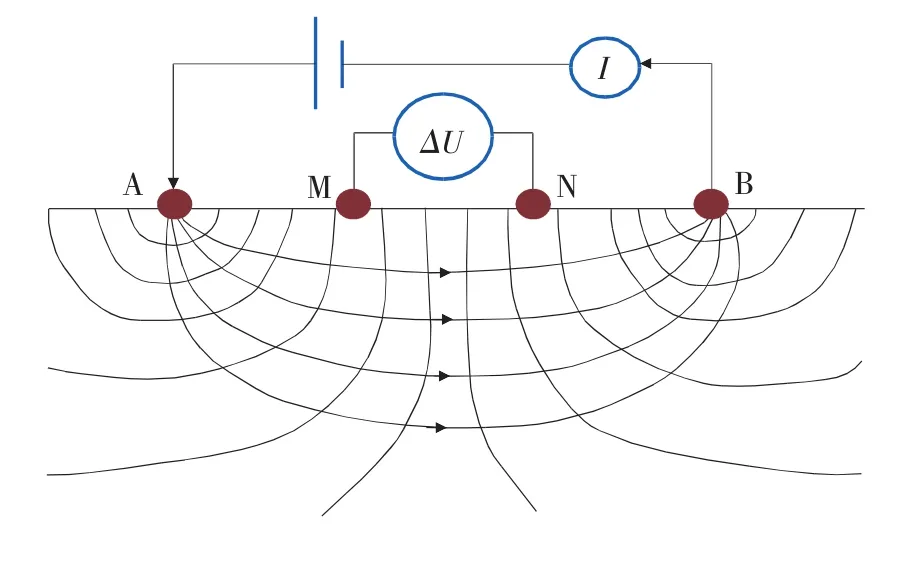
圖1 四電極測量原理
1 動力鋰電池內(nèi)部視電阻率測量裝置
1.1 測量原理
采用四電極測量原理,如圖1所示。在A、M、N、B 4個橫向排列的電極陣列中,對激勵電極A、B持續(xù)施加脈沖電流,從而在電池內(nèi)部形成穩(wěn)定電場,測量電極M、N兩點間電勢差可反映探測區(qū)域的視電阻率情況,調(diào)整電極間距可有效改變探測深度。定義n為電極間距因子,即電極距AM與MN的比值,測量電極M、N位置保持不變,激勵電極A、B等間隔向兩邊移動,n可依次取1,2,3,…,k。改變測量電極間距MN,以相同方式移動激勵電極A、B進行測量可以增加探測深度,盡可能獲取電池內(nèi)部不同區(qū)域的信息。
1.2 測量裝置
三維視電阻率測量系統(tǒng)如圖2所示,包括了三維傳感器單元、數(shù)據(jù)采集單元和圖像反演單元。三維柔性傳感器[11]主要由高可靠性柔性線路板(FPC)和電極陣列組成。數(shù)據(jù)采集單元進行信號采集及處理,處理后數(shù)據(jù)通過CAN總線傳輸至上位機,上位機對輸入數(shù)據(jù)進行電壓-電阻率轉(zhuǎn)換,通過圖像反演算法,對電池的內(nèi)部進行三維圖像重建,并構(gòu)造整體電池組內(nèi)部視電阻率分布的三維效果圖。
2 光滑約束高斯-牛頓三維反演成像算法
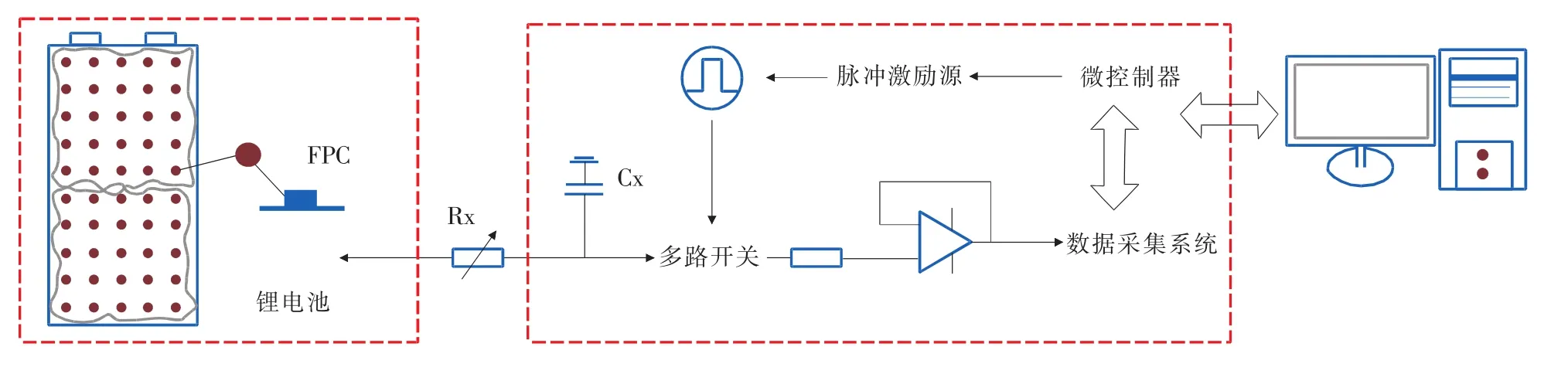
圖2 電池三維視電阻率測量系統(tǒng)
動力鋰電池內(nèi)部結(jié)構(gòu)ERT檢測技術(shù)的反演問題是一個非線性問題,本文在求解過程中將該非線性問題線性化,通過求解線性方程組,獲得非線性問題的解。若任意函數(shù)f(x)滿足級數(shù)理論條件,可以用泰勒級數(shù)表示在點p的鄰域里的函數(shù)f(x):
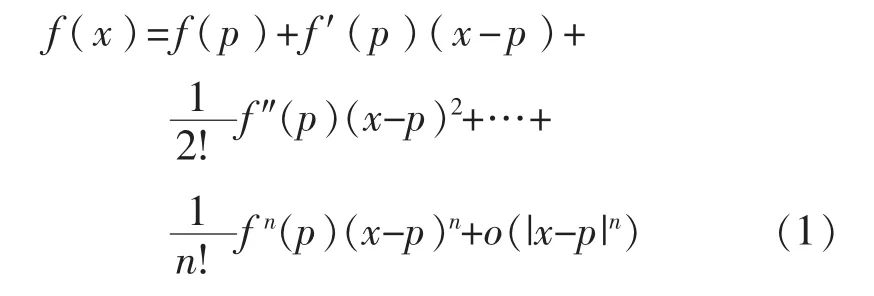
其中o(|x-p|n)表示高階無窮小,若取函數(shù)f(x)的一階近似為前兩項,則有:
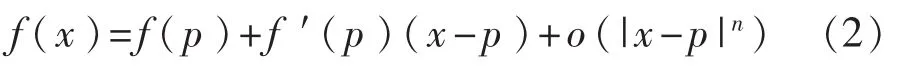
忽略一階無窮小,有:
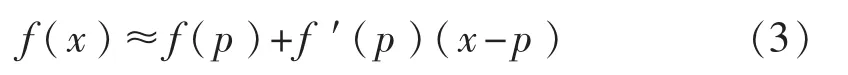
若x為N維向量,則:

其中:
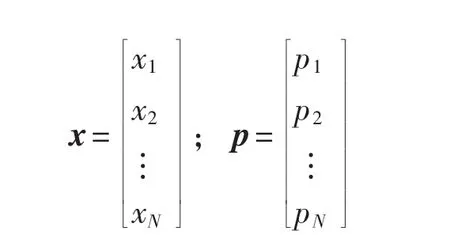
將式(4)應用于動力鋰電池內(nèi)部結(jié)構(gòu)狀態(tài)ERT反演非線性問題:
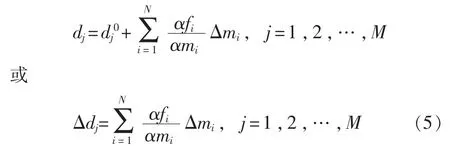
式中:dj——第j個觀測數(shù)據(jù);
mi——第i個模型參數(shù);
dj0——初始模型的第j個觀測數(shù)據(jù);
Δmi——mi的增量,Δmi=mi-mi0;
Δdj——dj的增量,Δdj=dj-dj0。
將式(5)寫成矩陣:

將式(6)正則化得到原理方程,即:

構(gòu)造目標函數(shù)ψ:
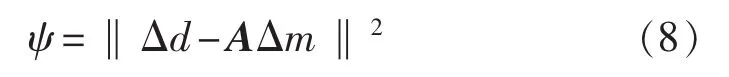
將目標函數(shù)對Δm求導并令其等于0,得到:
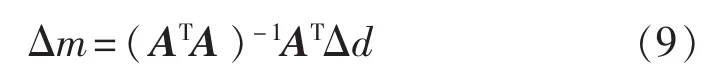
矩陣A為雅克比矩陣,求解式(9)可以得到模型的修正量Δm,將Δm加到起始模型m0得到更接近真實的新向量。然而,M>N,式(9)是一個超定方程。
矩陣ATA是嚴重病態(tài)的,導致式(9)為病態(tài)問題。將光滑約束引入反演方程可以解決這個問題。對于第i個網(wǎng)格而言,光滑約束可以表示為
式中:Δmi——第i個網(wǎng)格的模型參數(shù)修正量;
整個模型的光滑約束用矩陣表示為

其中F為光滑度矩陣。
標準高斯-牛頓算法,利用正演模型和實測數(shù)據(jù)構(gòu)造一目標函數(shù),并使其達到極小。光滑約束高斯-牛頓算法基于以下方程:
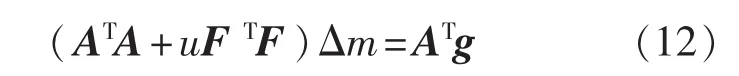
式中:FTF=FxFxT+FzFzT,F(xiàn)x為水平平滑濾波系數(shù)矩陣,F(xiàn)z為垂直平滑濾波系數(shù)矩陣;
u——阻尼系數(shù);
Δm——模型參數(shù)修正量;
g——數(shù)據(jù)殘差矢量,其值等于實測電阻率對數(shù)值與模擬的視電阻率對數(shù)值之差。
二、三維反演過程中對方程式偏導數(shù)矩陣的計算方式有所不同,二維反演對應的偏導數(shù)矩陣為二維計算,三維反演對應的偏導數(shù)矩陣為三維計算,偏導數(shù)矩陣的計算方式不同,導致了二、三維反演效果的不同。
通過對方程組進行求解,得到模型參數(shù)修正矢量,將其代入下式:
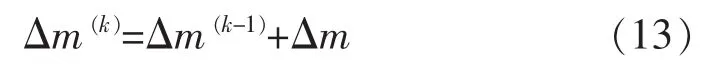
便得到新預測模型參數(shù)向量Δm(k)。重復這個過程直至實測數(shù)據(jù)和模擬數(shù)據(jù)之間的平均均方誤差RMS滿足要求為止,電阻率反演過程結(jié)束。

3 實驗研究
3.1 實驗平臺
動力電池內(nèi)部三維視電阻率測量平臺如圖3所示,實驗對象為鋁殼磷酸鐵鋰動力電池,尺寸140mm× 65mm×18mm。電極片為直徑5mm、厚度0.6mm圓形銅電極片,電極中心間距為12mm。
試驗中,環(huán)境溫度為常溫26.7℃,雙極性脈沖電流幅值設(shè)定為1mA,幅值增益為1。測試過程中,橫向10個電極11個數(shù)據(jù)點,縱向5個電極2個數(shù)據(jù)點,5×10電極陣列共有75個數(shù)據(jù)點,每個數(shù)據(jù)點重復測量6次。

圖3 動力電池內(nèi)部三維視電阻率測量平臺
3.2 性能驗證實驗
實驗將動力鋰電池與冰塊接觸,通過冰塊的局部降溫使得電池內(nèi)部的視電阻率分布呈現(xiàn)出與溫度變化相對應的變化,通過成像結(jié)果與冰塊實際放置位置的比較驗證成像算法的保真度。
在對未放置冰塊的動力鋰電池進行數(shù)據(jù)采集,獲取3組數(shù)據(jù)后,將體積為212.55 cm3的半圓柱體冰塊置于電池右側(cè)下方并與之緊密接觸,接觸面積為70.85cm2,如圖4所示。冰塊放置后對動力鋰電池每隔30s采集一次數(shù)據(jù),獲取5組數(shù)據(jù),隨后每隔1min采集一次數(shù)據(jù),獲取4組數(shù)據(jù),共獲取9組數(shù)據(jù)。實驗選取了電池的前后左右側(cè)共4個位置放置冰塊,每個位置均獲取9組數(shù)據(jù),實驗結(jié)果一致。本文僅對其中一組實驗結(jié)果進行詳細描述。

圖4 冰塊放置示意圖
在Matlab平臺上將系統(tǒng)輸出的電壓值換算為視電阻率,然后把各測點的坐標與視電阻率值對應起來,采用光滑約束高斯-牛頓算法對視電阻率進行圖像反演,得到動力電池內(nèi)部的視電阻率分布。
通過式(15)將電壓數(shù)據(jù)轉(zhuǎn)換視電阻率:

電流I為5×10-4A,放大倍數(shù)k=5000,參數(shù)G不同層數(shù)據(jù)點取值不一樣,第 1層數(shù)據(jù)點 G=2π· 0.012,第2層數(shù)據(jù)點G=2π·0.024。電壓數(shù)據(jù)為十六進制,需要換算為十進制,參照式(16)換算。
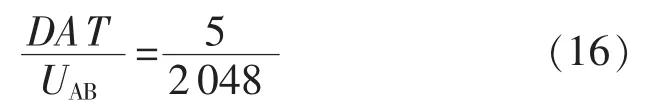
9組數(shù)據(jù)的換算結(jié)果如圖5所示,1~7數(shù)據(jù)點為第1層數(shù)據(jù),8~11數(shù)據(jù)點為第2層數(shù)據(jù),第2層數(shù)據(jù)點視電阻率明顯高于第1層數(shù)據(jù)點視電阻率,說明隨著深度增加,視電阻率上升。在放置冰塊1min 30s到2 min之間的30 s內(nèi)視電阻率發(fā)生明顯變化,因此選擇這兩個時刻的數(shù)據(jù)進行圖像反演,通過對比進行分析。
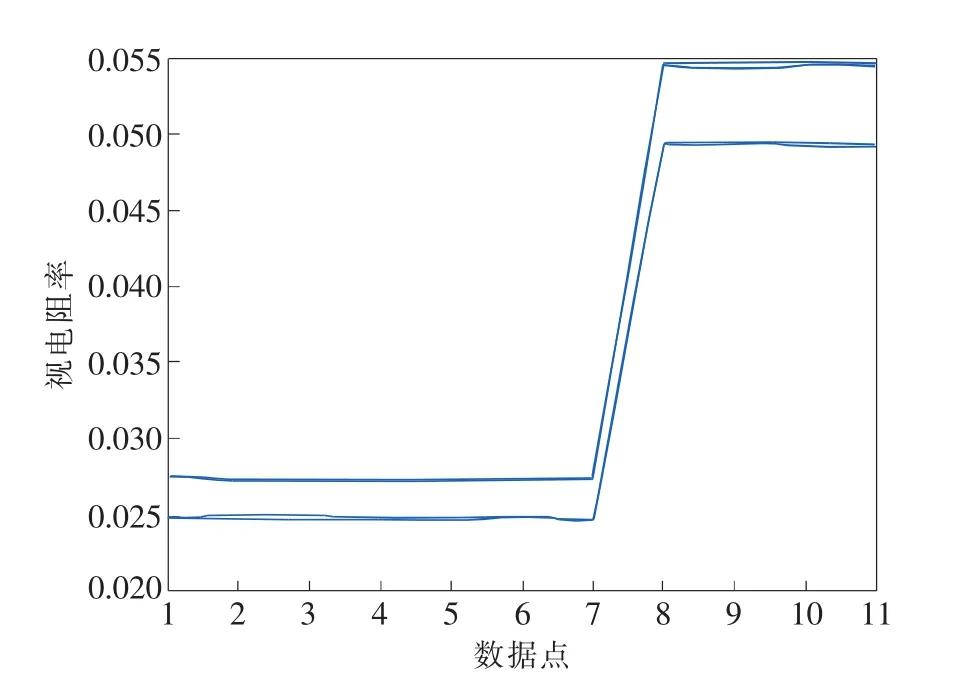
圖5 各組視電阻率的數(shù)據(jù)點分布
3.2.1 一致性驗證
動力鋰電池內(nèi)部狀態(tài)ERT三維反演結(jié)果如圖6所示,三幅圖像描述了動力鋰電池不同深度方向上每一層模型靈敏度的剖面分布圖,從而構(gòu)建起動力電池三維模型靈敏度分布。電池測區(qū)根據(jù)深度分為3個區(qū)域,這3個區(qū)域的模型靈敏度基本上是依次減少的(從區(qū)域1到區(qū)域3),這充分說明電流密度隨深度增加而逐漸衰減。同時,淺層區(qū)域模型靈敏度分布更加均勻,說明動力電池表層電流強度大,電流密度能夠均勻覆蓋整個淺層區(qū)域。
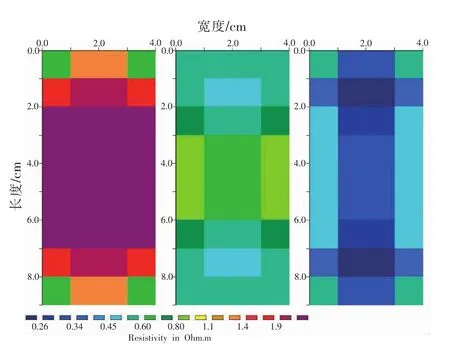
圖6 動力電池的反演模型靈敏度分布
圖7描述了動力電池在9次迭代后的內(nèi)部視電阻率反演圖像,不同色帶值表征動力電池內(nèi)部不同區(qū)域材料視電阻率值。可以看出動力電池在不同深度層上的色帶值存在毛刺和斷層,這些細節(jié)特征通常可以用來判斷動力電池內(nèi)部材料結(jié)構(gòu)組成的變化趨勢。對比圖7(a)和圖7(b),冰塊組的視電阻率整體較低,符合視電阻率與溫度的變化關(guān)系;圖7(a)視電阻率整體呈中心對稱分布,圖7(b)標記處兩側(cè)分布不對稱,因為右側(cè)接近冰塊,溫度較左側(cè)更低,因此相對應區(qū)域的視電阻率更低。反演結(jié)果與實際情況相符,能夠很好地反映多次內(nèi)部結(jié)構(gòu)視電阻率分布變化趨勢。圖8左側(cè)為動力電池內(nèi)部視電阻率三維反演圖像整體圖,右側(cè)為Y軸方向剖面圖。
在實際評價體系中,反演誤差RMS通常用來衡量最終成像效果,通過多次反演發(fā)現(xiàn)在進行10次迭代后反演平均均方誤差RMS改變不明顯,為3.34%。圖9為測量視電阻率與計算視電阻率的反演誤差RMS,整體上反演圖像效果良好,說明視電阻率數(shù)據(jù)整體性能優(yōu)良。
3.2.2 保真度驗證
評價ERT反演圖像的精度一般采用平均均方誤差RMS,但是,具有最小RMS值的模型有時顯示較大的、不實際的視電阻率值,因此具有最小RMS誤差的模型并不一定是與實際情況最接近的模型,最保守的模型應該選擇每次迭代后RMS的改變不明顯的模型。為了檢驗光滑約束高斯-牛頓算法的成像質(zhì)量,將光滑約束高斯-牛頓算法與常規(guī)高斯-牛頓迭代算法進行比較。以放置冰塊的實驗對象為測試模型。表1給出了光滑約束高斯-牛頓算法與常規(guī)高斯-牛頓迭代算法分別迭代5次、10次、20次圖像反演結(jié)果,表2給出了兩種反演算法的圖像反演誤差RMS。
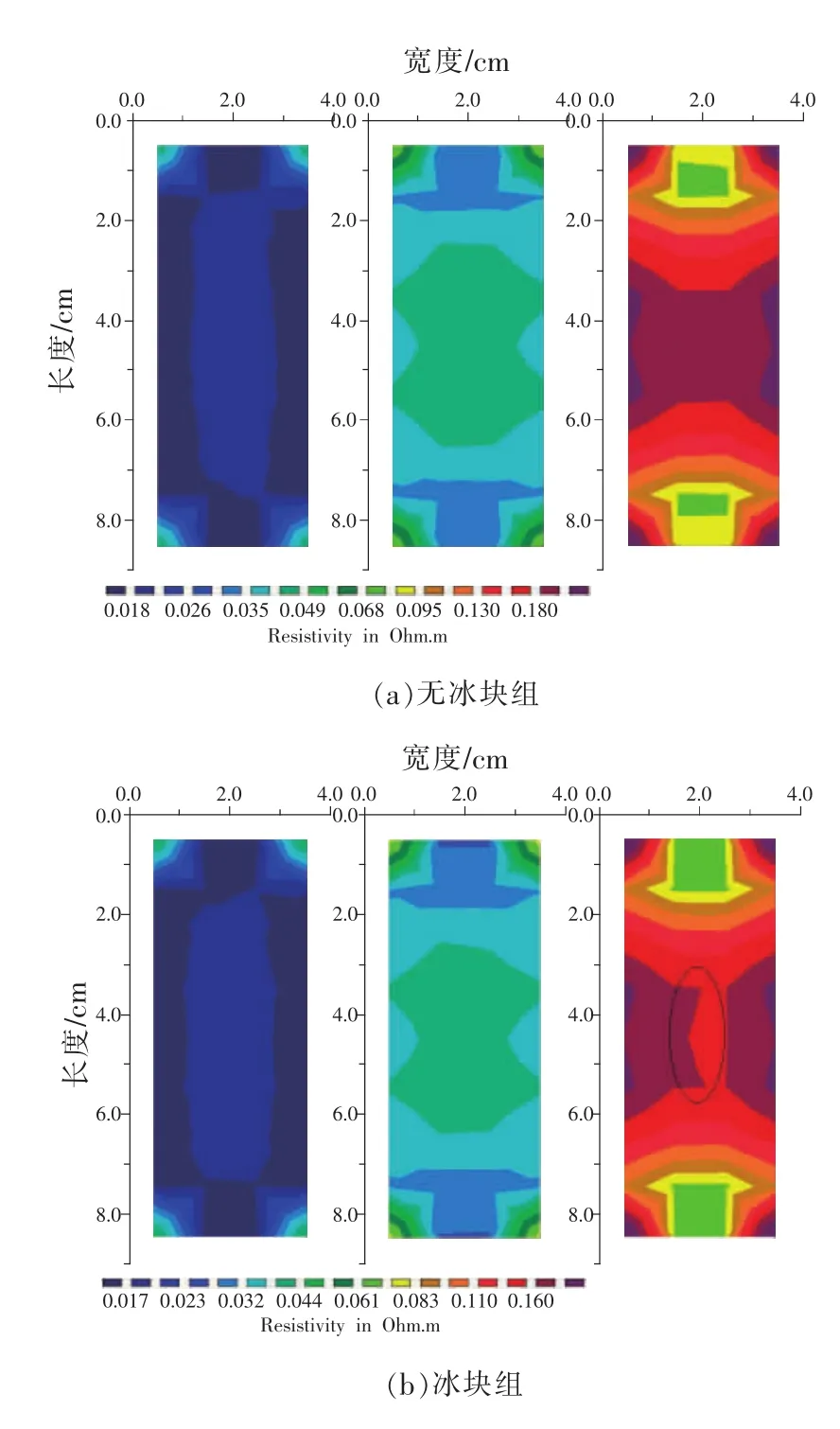
圖7 動力電池內(nèi)部視電阻率三維反演圖像截面圖
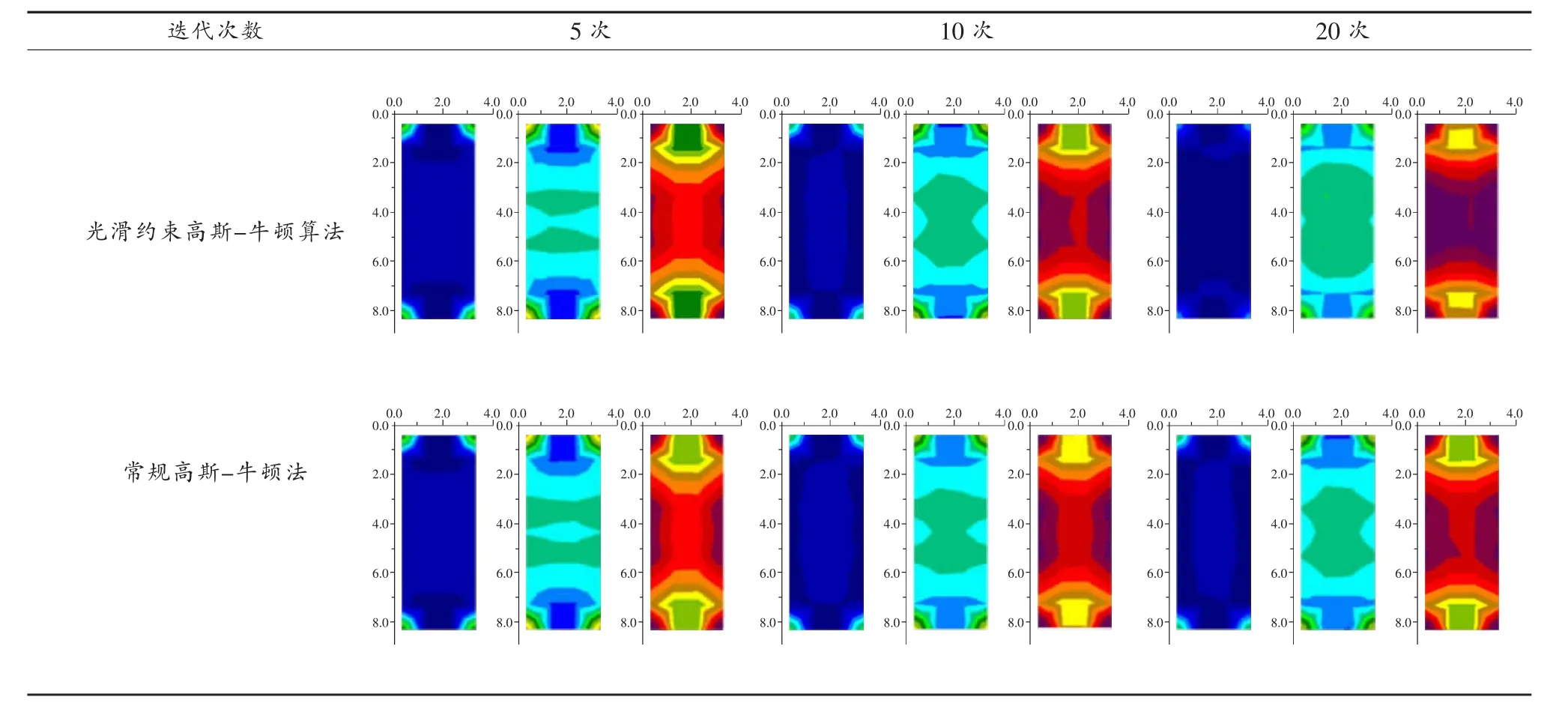
表1 兩種算法反演圖像比較
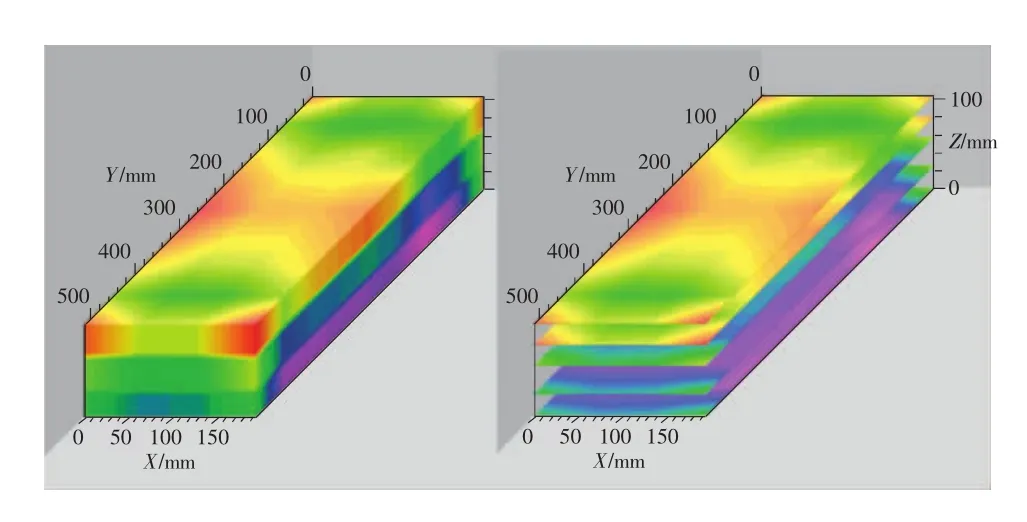
圖8 動力電池內(nèi)部視電阻率三維反演圖像整體圖
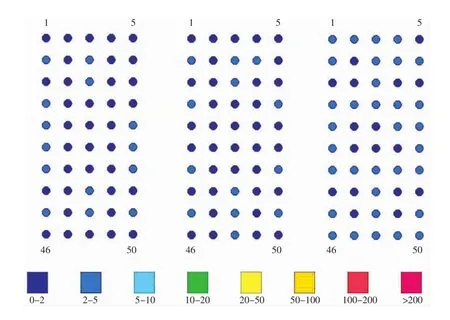
圖9 測量視電阻率與計算視電阻率的反演誤差RMS
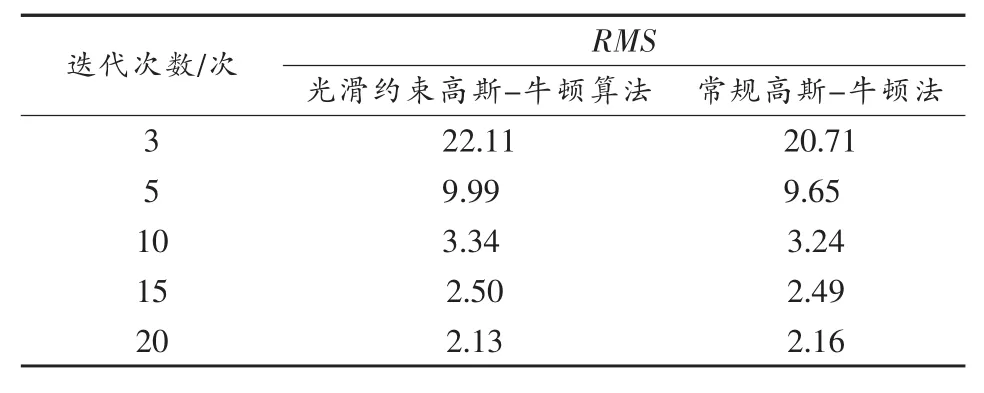
表2 兩種算法圖像反演誤差比較
可以看出,光滑約束高斯-牛頓算法質(zhì)量優(yōu)于常規(guī)高斯-牛頓法。光滑約束高斯-牛頓算法在迭代9次、10次左右的成像效果與常規(guī)高斯-牛頓法迭代20次的成像效果接近。從誤差指標RMS看出,兩種算法相同迭代次數(shù)下的RMS接近,光滑約束高斯-牛頓算法的RMS變化相對較穩(wěn)定,標準差小。
電池的一致性和優(yōu)越性是評價三維成像技術(shù)的一個重要手段。通過實驗,說明該三維圖像重建算法效果穩(wěn)定,能夠反映動力電池內(nèi)部的視電阻率變化趨勢,對動力電池內(nèi)部的視電阻率分布做出有效評估,滿足實際測量需求。
4 結(jié)束語
為了滿足電阻層析成像圖像重建算法應用于動力電池內(nèi)部結(jié)構(gòu)監(jiān)測領(lǐng)域的精度與實時性要求,本文提出對標準高斯-牛頓算法施加光滑約束進行圖像反演,使迭代步長在保證收斂的情況下達到最優(yōu)化,這樣就可以有效地提高成像的精度。結(jié)合實驗對提出的光滑約束高斯-牛頓圖像反演算法效果進行評估。實驗結(jié)果表明,該三維圖像反演算法效果穩(wěn)定,10次迭代后反演誤差RMS為3.34%,提高了檢測效率,擴大了檢測范圍,能夠反映動力電池內(nèi)部的視電阻率變化趨勢,對動力電池內(nèi)部的視電阻率分布做出有效評估,滿足實際測量需求。
[1]OH S H,KIM M,LEE J B.Influence of safety valve pressure on gelled electrolyte valve-regulated lead/acid batteries under deep cycling applications[J].Journal of Bulletin of the Korean Chemcal Society,2002,23(1):75-80.
[2]MCCLEARY D A H,MEYERS JP,KIM B.Threedimensional modeling of electro-chemical performance and heat generation of spirally and prismatically wound lithium-ion batteries[J].Journal of the Electrochemical Society,2013,160(11):1931-1943.
[3]于申軍,周永超.內(nèi)阻差異對鋰離子電池組安全性能的影響[J].化工學報,2010,61(11):2960-2964.
[4]TYAGI R C,MATHUR R S.Measurement of high temperature thermal conductivity of metals[J].Journal of Physics D:Applied Physics,1970(3):1811-1815.
[5]NICK P,WILLIAM R B L.A matlabtoolkit for threedimensional electrical impedance tomography:A contribution to the electrical impedance and diffuse optical reconstruction software project[J].Meas Sci Technol,2002,13(12):1871-1883.
[6]ZHDANOV M S,YOSHIOKA K.Cross-well electromagnetic imaging in three dimensions[J].Exploration Geophysics,2003,34(1-2):34-40.
[7]DOETSCH J,LINDE N,VOGT T,et al.Imaging and quantifying salt-tracer transport in a riparian groundwater system by means of 3D ERT monitoring[J].Geophysics,2012(77):207-218.
[8]徐光捷,楊獻勇,陳鷗.電阻層析成像場域的三維仿真[J].清華大學學報,2005,45(2):231-234.
[9]李守曉,王化祥.基于三維模型的改進正則化ERT成像算法[J].天津大學學報,2012,45(3):215-220.
[10]洪曉斌,李年智,尹文偉.基于電阻層析成像的汽車動力電池內(nèi)部溫度監(jiān)測[J].光學精密工程,2014,22(1):193-203.
[11]洪曉斌,李年智,謝爍熳,等.動力電池內(nèi)部視電阻率三維測量裝置設(shè)計[J].中國測試,2015,41(1):61-65.
(編輯:李剛)
Three-dimensional image reconstruction of apparent resistivity for power battery cell
XIE Shuoman,XU Weiying,HONG Xiaobin
(School of Mechanical Engineering,South China University of Technology,Guangzhou 510640,China)
Aiming to make image reconstruction algorithm for electrical resistance tomography(ERT)meet the acquirement of measurement for monitoring of internal structure of power battery in terms of precision and real-time,a newalgorithm for three-dimensional ERT image reconstruction is proposed.With the characteristics of the Gauss-Newton algorithm,the standard Gauss-Newton algorithm is applied to smooth constraint,which achieve the optimization of iteration step in the premise of ensuring convergence.The results showed that the algorithm of three-dimensional image with fast convergence and high accuracy improved the detection efficiency and expand the detection range;the algorithm can reflect the tendency of the apparent resistivity of the internal structure of power battery and estimate the distribution of the apparent resistivity of the internal structure of power battery,which meet the need of the measurement.
apparent resistivity;three-dimensional image reconstruction;Gauss-Newton algorithm;power battery
A
:1674-5124(2017)02-0119-06
10.11857/j.issn.1674-5124.2017.02.024
2016-06-20;
:2016-08-05
廣東省科技計劃項目(2016B010108001);廣州市科技計劃項目(201607010171);佛山市科技創(chuàng)新專項資金項目(2014HK100265、2016AG100255)
謝爍熳(1992-),女,廣東揭陽市人,碩士研究生,專業(yè)方向為網(wǎng)絡(luò)化測量與智能傳感技術(shù)。
洪曉斌(1979-),男,廣東揭陽市人,教授,博導,博士,主要從事無損檢測技術(shù)與裝備/網(wǎng)絡(luò)化智能測控技術(shù)及應用研究工作。

