汽車轉向試驗臺加載系統慣性力補償策略研究

陳帥通, 駱艷潔, 麥云飛， 劉丹丹

(上海理工大學 機械工程學院，上海 200093)

汽車轉向試驗臺加載系統慣性力補償策略研究

陳帥通, 駱艷潔, 麥云飛， 劉丹丹

(上海理工大學 機械工程學院，上海 200093)

針對汽車轉向試驗臺加載系統的慣性力進行了補償方法研究，通過機理建模原理建立了汽車轉向試驗臺數學模型并得到簡化方框圖，求出方框圖中相應的傳遞函數，分析試驗臺中轉向器驅動系統和加載系統存在的耦合，并根據前饋補償解耦原理設計了前饋補償解耦控制器，以消除加載系統慣性力，最后將加載系統補償前后的模型進行了Simulink仿真。解耦仿真結果表明，加入前饋補償解耦器后，加載系統在不同頻率下具有較高的跟蹤精度，慣性力有效地得到補償。

轉向試驗臺；慣性力；前饋補償解耦；Simulink仿真

汽車轉向試驗臺是汽車轉向器功能測試和疲勞試驗的主要設備，是典型的被動式電液力伺服控制系統，主要由加載系統和轉向器驅動系統組成。工作過程中，液壓缸加載方式為被動加載，馬達主動運動對液壓缸造成強制位移擾動，此時不可避免地產生強迫流量[1]，流量的變化引起負載壓力的變化，從而產生了附加作用力，由此產生的慣性力將作用于測試設備，系統出現超調與抖動，不僅有損于機械零件，而且影響加載系統的控制性能和控制精度。因此,對汽車轉向試驗臺加載系統慣性力補償方法的研究就顯得相當重要。

目前對慣性力的補償方法研究主要分為兩大類：一類是硬件結構補償法，另一類是運動控制補償法。從目前的成果來看，硬件結構補償具有穩定性好、可靠性高等優點，但是對裝配精度和機械加工要求比較高，如蓄能器校正；控制補償法中的結構不變性原理被廣泛應用，但結構補償加載系統在中高頻時跟蹤滯后，導致慣性力得不到有效的補償[2-3]。

國內外學者對慣性力補償問題進行了一系列的研究。ETO等[4-5]研制的無閥控制加載系統，運用定量反饋理論設計控制器來消除慣性力；CARTER等[6]采用了加載馬達兩腔安裝蓄能器來抑制慣性力；王新民等[7]采用類似于PID形式的內部反饋控制方法。

本文針對汽車轉向試驗臺的特點，采用了前饋補償解耦控制方法解除加載系統和轉向器驅動系統之間的耦合，從而達到補償慣性力的目的。

1 轉向試驗臺數學建模建立

汽車轉向試驗臺控制結構原理如圖1所示,由轉向器驅動系統和模擬負載的加載系統兩部分組成。轉向器驅動系統是由模擬方向盤轉動的液壓馬達以及電液伺服閥、角度編碼器等組成，為主動加載系統，由液壓站提供液壓油，電液伺服閥輸出流量和壓力信號，來控制液壓馬達模擬方向盤轉動。模擬負載的加載系統由兩個閥控液壓缸以及電液伺服閥、力傳感器等組成，為被動加載系統，用來模擬汽車輪胎所受路面摩擦等載荷。由于本論文試驗臺左右兩側加載系統完全相同，現僅研究試驗臺右側加載系統。

圖1 轉向試驗臺結構原理圖Fig.1 Structure diagram of automobile steering test bench

在加載系統中，兩套閥控缸完全相同，可將其看作零開口四通閥控液壓缸；放大器頻帶較寬，可視為比例環節；電液伺服閥的傳遞函數可用慣性環節表示；大多情況下，力傳感器的帶寬比系統的帶寬大很多，所以力傳感器的傳遞函數可以近似看成比例環節。根據文獻[8]可知加載系統的數學模型及其方框圖，見圖2。

圖2 加載系統方框圖Fig.2 Block diagram of load system

圖2中，m為負載的折算質量，Kq為伺服閥在穩態工作點附近的流量增益，Xv為伺服閥閥芯位移，Kc為伺服閥流量-壓力系數，A為液壓缸活塞有效面積，Vt為液壓缸兩個油腔的總容積，βe為液壓油彈性模數，K為負載的折算剛度，Ka為放大器增益，Ur1為計算機輸入的電壓信號，Kv為伺服閥增益，Tv為伺服閥時間常數，UF為力傳感器輸出的反饋電壓，KF為力傳感器增益，Fc為力傳感器檢測到的驅動力,Y2為機械位移干擾量。

在轉向器驅動系統中，液壓馬達角度控制模塊是用伺服閥控制馬達的流量，以實現控制液壓馬達的轉動角度。現在假設液壓馬達的負載由慣性力、彈性力、黏性摩擦力和外力組成，可以求出滑閥的線性化流量方程和液壓馬達的流量連續方程、力平衡方程，液壓油與負載質量組成的模塊可以簡化成一個質量-彈簧阻尼的二階震蕩模塊。根據文獻[9]可知轉向器驅動系統的數學模型及其方框圖，如圖3所示。

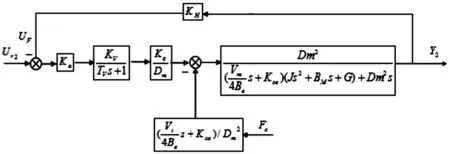
圖3 轉向器驅動系統方框圖Fig.3 Block diagram of steering gear drive system

圖3中，Dm為液壓馬達的平均理論排量，Vm為液壓馬達內腔和連接管道的總容積，J為液壓馬達和負載的總慣量，BM為負載和液壓馬達的粘性阻尼系數，G為負載的扭轉彈簧剛度，KH為角度編碼器系數。

由圖2和圖3可以得到汽車轉向試驗臺的簡化方框圖，如圖4所示。

圖4 汽車轉向試驗臺簡化方框圖Fig.4 Simplified block diagram of vehicle steering test bench

2 加載系統前饋補償解耦

前饋補償解耦實際上是把某個單回路通道的輸出對其它單回路通道的影響看作是一種擾動作用[10]，然后設計一個解耦控制器，用它去解除控制回路間的耦合，消除擾動作用，以保證各個單回路的控制系統能正常工作。

由圖2、3、4求出傳遞函數B11、B12、B21、B22為：

(1)

(2)

(3)

(4)

(5)

變換得：

(6)

其中：

(7)

轉向器驅動系統的角度輸出對加載系統產生強制位移擾動Y2，加載系統的輸出力Fc對轉向器驅動系統產生扭矩干擾，轉向器驅動系統與加載系統之間相互影響、相互耦合，耦合的存在是慣性力產生的根本原因。如圖4所示，UΔ1的改變對Y2、Fc同時發生影響，UΔ2的改變對Y2、Fc同時發生改變，為了實現UΔ1與Fc之間、UΔ2與Y2之間的解耦，現設計解耦控制器應用到轉向試驗臺系統得到解耦后方框圖，見圖5。

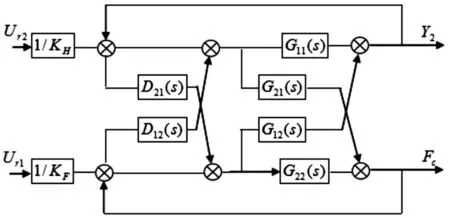
圖5 解耦后轉向試驗臺方框圖Fig.5 Block diagram of the steering test bench after decoupling

根據前饋補償解耦原理，由圖5可得：

Ur2(s)D21(s)G22(s)+Ur2(s)G21(s)=0

(8)

Ur1(s)D12(s)G11(s)+Ur1(s)G12(s)=0

(9)

根據式(5)～式(6)，可得前饋補償解耦控制器傳遞函數為：

(10)

(11)

根據式(1)～(8)求出前饋補償解耦傳遞函數D21(s)、D12(s)如下：

(12)

(13)

3 加載系統解耦仿真

根據表1參數，在MATLAB/Simulink仿真環境下建立加載系統仿真模型。轉向器驅動系統位置擾動為正弦信號y2(t)=ysin 4πt，幅值為y，t為時間變量；加載系統輸入信號為ur1=usin 8πt，u為幅值，t為時間變量。

表1 閥控液壓缸參數

令ur1=0，即加載系統輸入力信號為零，在不添加前饋補償解耦情況下，得到加載系統在位置擾動作用下的輸出波形如圖6曲線1所示，此曲線為未采用前饋補償解耦器前的系統中的慣性力大小的反應，由曲線可知，即使液壓缸不對加載系統加載(輸入力信號為零)，但仍有較大輸出力。圖6曲線2為系統采用本文提出的前饋補償解耦器后的輸出波形，波形較為平穩，輸出力小。由解耦補償前后慣性力曲線對比可知，未添加前饋補償解耦時慣性力大，在系統啟動瞬間大概0.3 s的時間內，慣性力超調量很大且震蕩頻繁，嚴重影響系統控制精度；采用前饋補償解耦后，加載系統輸出力明顯變小，系統慣性力有效地得到補償。

圖7(a)、(b)分別為強制位移干擾信號和加載輸入信號，圖8為系統未添加前饋補償解耦時的液壓缸輸出力對比響應曲線，曲線1為加載輸入信號，曲線2為伺服缸輸出力信號。由于強制位移干擾的作用，慣性力導致曲線嚴重失真，尖峰十分明顯，當液壓馬達分別在0.04、0.1、0.17、0.33、0.4、0.46 s換向瞬間，此時速度發生突變，引起加載系統強烈震動，曲線嚴重超調。圖9為添加前饋補償解耦后的伺服缸輸出力對比曲線，曲線1為加載輸入信號曲線，曲線2是液壓缸輸出力信號曲線，曲線波形平穩。由圖8和圖9對比可知，前饋補償解耦器極大地消除了強制位移造成的干擾。

圖6 慣性力對比曲線Fig．6Inertiaforcecontrastcurve (a) 強制位移干擾信號 (b) 加載輸入信號圖7 強制位移干擾信號和加載輸入信號Fig．7ForceddisplacedinterferencesignalandLoadinputsignal

圖8 補償前輸出力對比Fig 8 Contract curve of output force beforce compensation

圖9 補償后輸出力對比Fig 8 Contract curve of output force after compensation

為進一步證明文中前饋補償解耦的有效性，對閥控液壓缸加載系統在不同頻率下進行跟蹤精度分析。圖10～圖12為加載系統采用本文所提的前饋補償解耦后、在頻率分別為1 Hz、3 Hz、5 Hz時的正弦跟蹤精度響應曲線。從圖10(a)～圖12(a)分析看出，加載系統在最高頻率5 Hz情況下仍能夠較精確地對加載系統輸入信號進行跟蹤，輸出信號較準確地復原了輸入信號；從圖10(b)～圖12(b)分析看出，隨著頻率的提高，系統的力跟蹤誤差也隨之提高，在最大5 Hz的頻率下，力跟蹤誤差為5%，仍具有較高的跟蹤性能；由曲線可看出在系統啟動瞬間大概0.05 s時間內，跟蹤誤差曲線有極小的超調，但迅速趨于穩定。

4 結 論

本文對汽車轉向試驗臺加載系統進行了慣性力補償策略研究，設計了前饋補償解耦器，通過加載系統解耦仿真得到以下結論：

(a)力跟蹤曲線(a)力跟蹤曲線(a)力跟蹤曲線

(b)力跟蹤誤差圖10 頻率為1Hz時的力響應曲線Fig．10Forceresponsecurveat1Hzfrequency(b)力跟蹤誤差圖11 頻率為3Hz時的力響應曲線Fig．11Forceresponsecurveat3Hzfrequency(b)力跟蹤誤差圖12 頻率為5Hz時的力響應曲線Fig12Forceresponsecurveat5Hzfrequency

(1)由于馬達角度輸出對加載系統造成強制位移干擾的作用，液壓缸輸出力中附加多余的慣性力，影響系統的控制精度。

(2)前饋補償解耦器解除了轉向器驅動系統與加載系統之間的耦合，消除了干擾作用，加載系統的慣性力有效地得到補償。

(3)解耦后加載系統啟動瞬間仍有極小超調，力跟蹤仍有誤差，為系統本身結構造成。

[ 1 ] 郝經佳，趙克定，許宏光.雙閥控制在電液負載仿真臺中的應用[J]. 機械工程學報，2002，13(10):813-816. HAO Jingjia，ZHAO Kingding，XU Hongguang.Appliation of double valve control in electric power load simulation platform.[J]. Journal of Mechanical Engineering，2002，13(10):813-816.

[ 2 ] YAO Jianjun，WANG Xiancheng，WU Zhenshun.Variable structure control applied in electro-hydraulic servo system with ann[J]. Chinese Journal of Mechanical Engineering,2006，19(1)：32-36.

[ 3 ] 李水聰.被動式電液力伺服解耦控制研究[D].洛陽：河南科技大學，2012.

[ 4 ] ETO Y， ENDO N.Real-Time simulator for Torque split control system[J]. JSAE REVIEW，1995，16(4):391-395.

[ 5 ] KAISER M J，WEEKS W L.Electro-Hydrodynamic simulator Investigations[J]. Mathematics and Computers in Simulation，1994，36(3)：221-240.

[ 6 ] CARTER W J，LEE D C，SIMEONE V A，et al.Aeroload torque simulator[P].United States Patent 4235103,November 25，1980.

[ 7 ] 王新民，劉衛國.被動加載的內部反饋控制方法[J]. 中國機械工程，2006，17(23):2447-2450. WANG Xinmin，LIU Weiguo.Passively loaded internal feedback control method[J]. China Mechanical Engineering，2006，17(23):2447-2450.

[ 8 ] 顧凱凱，麥云飛，駱艷潔. 汽車轉向器試驗臺數學模型設計和仿真[J]. 現代制造工程，2012(1):31-35. GU Kaikai，MAI Yunfei，LUO Yanjie.Mathematical model design and Simulation of automobile steering gear test bench[J]. Modern Manufacturing Engineering,2012(1):31-35.

[ 9 ] 盧翔，駱艷潔，麥云飛. 動態加載系統慣性力控制方法研究[D].上海：上海理工大學，2014

[10] WITTENMARK B, MIDDLETON R, GOODWIN G C.Adaptive decoupling of multivariable systems[J]. Int J control，1987，46(6):1993-2009.

[11] 吳振順，液壓控制系統[M]．北京：高等教育出版社，2008

[12] 許小慶，權龍.利用速度控制抑制電液位置伺服系統沖擊的方法[J]. 振動與沖擊，2013，32(2):107-110. XU Xiaoqing，QUAN Long.Method for restraining the impact of the electro hydraulic position servo system using speed control[J]. Journal of Vibration and Shock，2013，32(2):107-110.

[13] NAM Y S，SUNG K H. Force control system design for aerodynamic load simulator[J]. Control Engineering Practice，2002,10(5):549-558.

[14] JIAO Zongxia, GAO Junxia, HUA Qing,etal .The velocity synchronizing control on the electro-hydraulic load simulator[J]. Chinese Journal of Aeronautics，2004，17(1):106-109.

[15] 沈剛,朱真才,李翔,等.三軸六自由度電液振動臺解耦控制[J].振動與沖擊,2015,34(19):1-7. SHEN Gang,ZHU Zhencai,LI Xiang,et al.Decoupling control for a triaxial 6-DOF Electro-hydraulic shaking table[J].Journal of Vibration and Shock,2015,34(19):1-7.

Inertia force compensation strategy for loading system of a vehicle steering test bench

CHEN Shuaitong, LUO Yanjie, MAI Yunfei, LIU Dandan

(School of Mechanical Engineering，University of Shanghai for Science and Technology, Shanghai 200093, China)

The compensation method for inertia force of load system of a vehicle steering test bench was studied. Through mechanism modeling, the mathematical model of the vehicle steering test bench was established, and the corresponding transfer function was derived. The coupling between steering gear drive system and loading system was analyzed. According to the decoupling principle of feed-forward compensation, the feed-forward compensation decoupling controller was designed to eliminate the inertia force of the loading system. Finally, Simulink simulation was conducted for the model before and after the compensation of the loading system. The simulation results showed that after adding the feed-forward compensation decoupling controller, the loading system has a higher tracking accuracy at different frequencies, and the inertia force is better compensated.

steering test bench; inertia force; feed-forward compensation decoupling; Simulink simulation

上海市自然科學基金(13ZR1458500)

2015-10-19 修改稿收到日期：2016-01-26

陳帥通 男，碩士生，1990年6月生

麥云飛 男，副教授，碩士生導師，1964年11月生

TP302

A

10.13465/j.cnki.jvs.2017.03.038