非共面基座的不對等精度平臺慣組主從冗余控制技術

胡任祎 賀彥峰 崔瑩瑩

北京航天自動控制研究所，北京 100854

隨著航天技術的不斷發展進步，不僅對飛行器的控制精度要求越來越高，而且對整個飛行過程中導航控制系統的可靠性和故障容錯能力的要求也日益提升，以確保飛行器在各種復雜條件下均能正確完成任務。慣性測量器件是導航控制系統的核心關鍵部件[1]，目前為了提高導航控制系統的可靠性，除了通過進一步提升慣性測量器件的設計、加工和制造水平外，另外一種經濟而便捷的途徑就是通過慣性測量器件的冗余技術，有效提高導航控制系統的可靠性和故障容錯能力。

飛行器通常采用的慣性測量器件分為框架式平臺(以下簡稱平臺)和捷聯式慣組(以下簡稱慣組)2大類，冗余配置模式主要包括以下幾種：平臺+慣組主從冗余[2]、雙慣組主從冗余[3-4]、三慣組冗余[5]和單慣組多表冗余[6]等。慣性器件的故障診斷目前已發展出多種方法，如：閾值比較法[7]、小波變換法[8]、神經網絡法[9]、解析模型法[10]、支持向量機[11]、專家系統法[12]和等價空間法[13-14]等。這些冗余技術方案多數應用的前提是慣性測量器件之間儀表精度相當，且同時安裝在共同的測量基座上或具有相同的測量環境，而針對儀表精度差異較大且測量基座和環境不同的特殊情況，現有冗余技術方案或多或少存在一定局限性。針對上述問題，本文給出了一種適應工程實際應用的非共面基座的不對等精度平臺慣組主從冗余控制技術，能夠很好地解決上述問題，并通過仿真試驗對故障診斷方法和門限進行驗證。

1 慣性器件的冗余配置

在本文的應用環境中，平臺與慣組在原理結構、安裝位置和精度水平等幾個方面均存在較大差異。首先，平臺可直接提供發射慣性系中3個方向的視加速度信息參與導航控制，慣組敏感飛行器載體系3個方向的視加速度信息和角度信息，通過數學算法轉換得到發射慣性系視加速度和角度信息。其次，平臺安裝于飛行器中軸線上振動環境干擾相對較小的儀器艙內，自身通過物理機械框架結構為加速度計提供隔離了外界沖擊干擾的良好穩定的測量環境；慣組則安裝于距平臺較遠的邊緣位置，直接固連于載體上，飛行過程中飛行器載體本身的結構擾動、振動干擾、彈性晃動以及繞質心運動帶來的桿臂效應均會影響慣組測量信息的輸出。最后，平臺測量精度水平高，但成本昂貴、結構復雜、體積偏大；慣組成本低廉、結構簡單、體積小巧，但精度水平較差。非共面基座的不對等精度平臺慣組主從冗余方案采用平臺為主、慣組為輔、熱備份的組合模式，既能有效化解平臺導航控制的可靠性風險，又能大幅控制由于采用冗余技術帶來的成本開銷。

平臺慣性測量器件配置采用3個沿正交軸分布的加速度計，敏感飛行器在慣性系中的視加速度矢量信息。

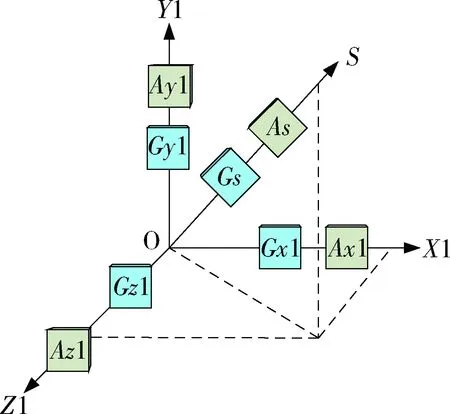
圖1 慣組慣性測量器件配置方式

慣組慣性測量器件配置方式如圖1所示，其中慣組采用4個陀螺儀和4個加速度計，分別敏感飛行器載體的角速度矢量和視加速度矢量信息。4個儀表按照3個正交軸和1個斜置軸的方式布局，根據空間幾何構型關系，3個正交軸上的矢量在斜置軸上的投影分量和與斜置軸矢量應大小一致，關系式如下：

S=k1X+k2Y+k3Z

(1)

式中，S,X,Y,Z分別表示斜置軸和正交軸的矢量大小，k1,k2,k3分別表示正交軸矢量在斜置軸上的投影系數。

2 主從冗余故障診斷

2.1 基本原則

與常見的冗余故障診斷的模式不同，考慮到平臺和慣組之間的精度水平差異巨大、測量環境不同、及使用方式的區別，平臺測量輸出的信息無法直接和慣組測量信息之間進行交叉對照比較，也無法進行單表級的信息重構，確定冗余故障診斷的基本原則如下：

1)平臺和慣組的測量信息不進行交叉互判；

2)以平臺為主進行飛行控制，只有平臺出現異常，同時慣組工作正常時，才切換到慣組飛行控制；

3)故障診斷的重構采用簡單模式，即平臺、慣組整體切換。

2.2 故障模型

慣性器件作為導航信息測量的重要來源進行冗余管理，必須明確其故障模式和類型，作為其冗余信息管理的依據。慣性器件故障成因復雜，表現多樣，存在無法認識的故障類型盲區。針對本文適用的慣性器件安裝配置方式，故障診斷的主要故障類型分為以下幾種：倒臺故障、零值故障、極大值故障和緩變故障。

倒臺故障：當平臺穩定隨動回路出現故障時，無法將平臺臺體穩定在慣性空間，平臺框架軸將出現高速旋轉，使得平臺姿態角輸出發散，最終導致飛行器姿態失穩，任務失敗。

零值故障：當陀螺儀和加速度計由于電源故障或者儀表卡死，使得儀表的輸出無法正常反映飛行器的真實運動特性，導致儀表輸出為0。

極大值故障：當陀螺儀和加速度計的相關電路出現異常，儀表飽和輸出，遠超正常值范圍。

緩變故障：當陀螺儀和加速度計的工具誤差系數穩定性出現異常，測量誤差逐漸偏離原有標定值，導致慣性導航輸出信息與飛行器實際狀態之間的偏差隨著時間的推移顯著增大。

2.3 冗余算法

主從冗余故障診斷的流程如圖2所示。

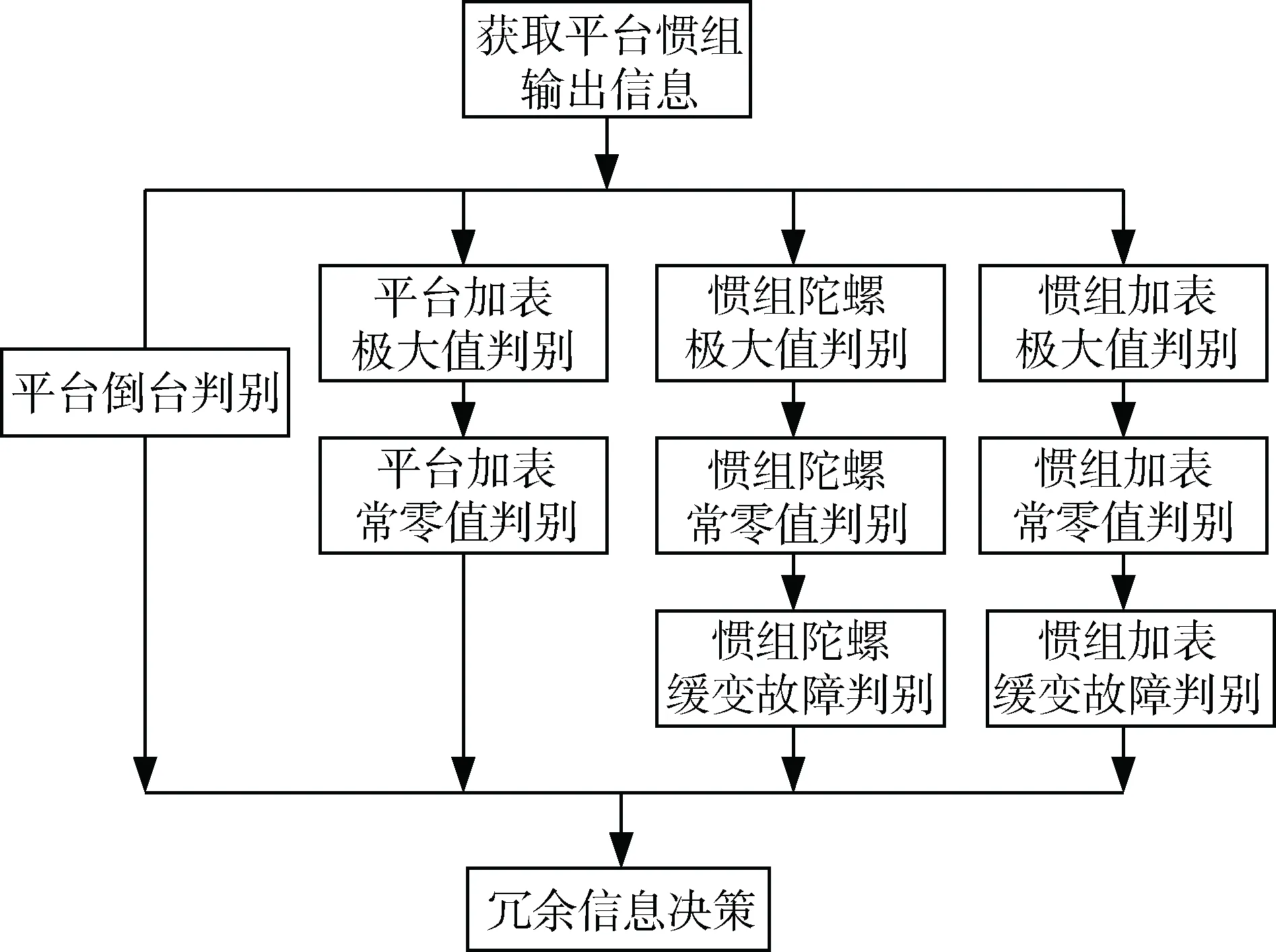
圖2 冗余故障診斷流程圖

1)平臺倒臺故障判別

在發生平臺倒臺故障的初期，平臺姿態角即已表現出非正常的變化速率，根據平臺姿態角計算其角速率，與平臺倒臺故障判別門限值進行比較，超過門限即認定發生平臺倒臺故障。判別算法為：

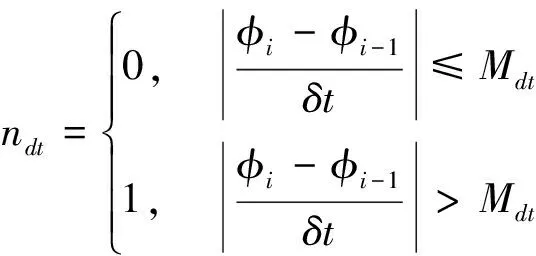
(2)

式中，φi和φi-1分別表示當前計算周期姿態角和上一個計算周期姿態角，δt表示計算周期的時間，Mdt表示平臺倒臺故障判別門限，ndt表示平臺倒臺故障標志字，0表示無故障，1表示有故障。

2)零值故障判別

平臺加表、慣組加表和慣組陀螺均存在零值故障模式，故障機理相似，因此判別的方式也相同。通過判別慣性儀表的脈沖輸出增量絕對值是否小于零值故障門限來檢測是否出現零值故障。其中，平臺和慣組的加表敏感視加速度信息，慣組陀螺敏感姿態角速度信息，因此在針對具體任務設計方案時，需對各測量軸在整個飛行段的受力情況和姿態角變化情況進行全面分析，合理選擇相應的零值門限。判別通用算法為：

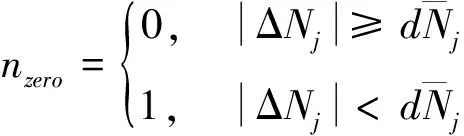
(3)

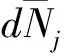
3)極大值故障判別

與常零值故障類似，平臺加表、慣組加表和慣組陀螺均存在極大值故障模式，判別方式也相同。通過將慣性儀表的脈沖輸出增量與極大值故障門限進行比較，如果超過門限，則認為發生極大值故障。判別通用算法為

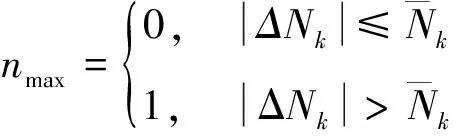
(4)

式中，ΔNk表示平臺加表、慣組加表或者慣組陀螺等慣性儀表各個測量方向上的輸出脈沖增量，nmax表示極大值故障標志字，0表示無故障，1表示有故障。

4)緩變故障判別

緩變故障相對其他幾種故障模式更為隱性，故障特征不顯著，需將3個正交表與1個斜置表的信息進行比較，并經過一段時間累積才能確認故障存在。慣組分別有4個陀螺儀和4個加速度計，具備緩變故障判別的條件；平臺只有3個正交表，沒有冗余信息，無法進行緩變故障的判別。在緩變故障判別時，先將各表測量信息進行工具誤差補償，補償后的3個正交表測量信息在斜表上的投影之和與斜置表之間的偏差應在某一合理范圍之內，如果偏差大于合理性門限，則認定存在緩變故障。判別算法為：

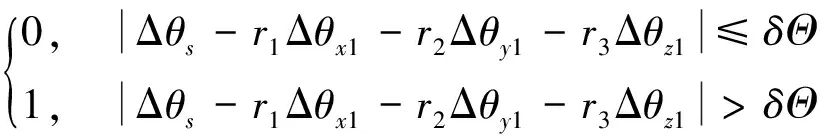
(5)

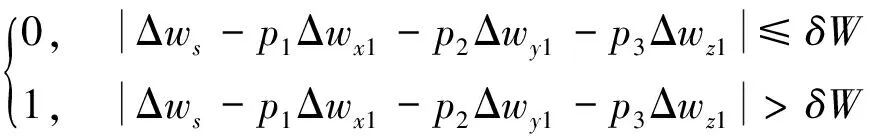
(6)

式(5)中，Δθs,Δθx1,Δθy1,Δθz1分別表示經過誤差補償后的斜置表和正交表陀螺儀的角增量，r1,r2,r3分別表示正交陀螺儀在斜置陀螺儀上的投影系數，δΘ表示陀螺儀緩變故障門限，nGself表示慣組陀螺儀緩變故障標志字，0表示無故障，1表示有故障。式(6)中，Δws,Δwx1,Δwy1,Δwz1分別表示經過誤差補償后的斜置表和正交表加速度計的視速度增量，p1,p2,p3分別表示正交加速度計在斜置加速度計上的投影系數，δW表示加速度計緩變故障門限，nAself表示慣組加速度計緩變故障標志字，0表示無故障，1表示有故障。

5)冗余信息決策

在平臺和慣組的輸出信息進行故障診斷完成后，需要匯總各儀表的故障診斷結果，進行綜合評估并決策最終冗余判別后參與飛行控制的慣性導航信息。冗余信息決策的核心思想遵循冗余管理的基本原則，同時考慮到平臺慣組的安裝環境和精度差異。冗余信息決策邏輯流程圖如圖3所示。

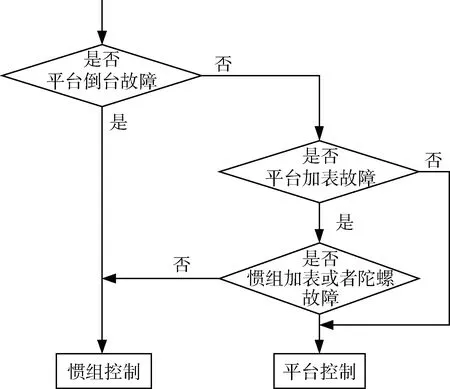
圖3 冗余信息決策邏輯圖

圖3中平臺加表故障指平臺加表零值故障或極大值故障，慣組加表故障指慣組加表零值故障、極大值故障或者緩變故障，慣組陀螺故障含義與慣組加表故障相同。

相對應的冗余信息決策真值表詳見表1所示。

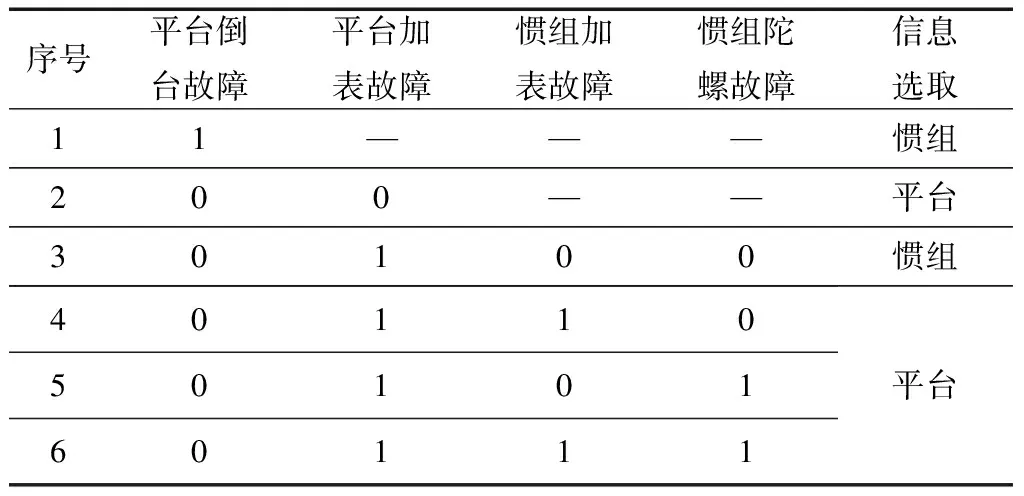
表1 冗余信息決策真值表

3 主從冗余故障診斷門限設計

門限設計主要涉及到平臺倒臺門限、極大值門限和緩變故障門限等3個方面。倒臺門限設計中暫時無完備的倒臺動態過程數學模型可供計算，一般根據歷史試驗數據，同時結合飛行器實際飛行過程中的動態數據，給出一個合理的倒臺故障門限。極大值門限設計主要考慮飛行器在各種狀態下的最大加速度情況，經過適當放大后，根據慣性測量儀表的當量即可折算出極大值門限。緩變故障門限設計與慣性測量儀表具體誤差模型密切相關，在設計過程中可適當對測量誤差影響很小的誤差項進行簡化。慣組陀螺角速率測量誤差計算式如下：

ΔΩ=H-1·δH·ω+H-1·δD0+
δG·ω+H-1·δG·D0

(7)

式中，ΔΩ為陀螺儀角速率測量誤差，H為陀螺儀安裝系數矩陣，δH為陀螺儀安裝系數隨機項誤差矩陣，D0為陀螺儀零次項誤差，δD0為陀螺儀零次項隨機誤差矩陣，δG為陀螺儀標度因素重復性誤差，ω表示各個測量軸方向上的角速度輸入值。

ΔW=M-1·δM·a+M-1·δE0+
δA·a+M-1·δA·E0

(8)

式中，ΔW為加速度計視加速度測量誤差，M為加速度計安裝系數矩陣，δM為加速度計安裝系數隨機項誤差矩陣，E0為加速度計零次項誤差，δE0為加速度計零次項隨機誤差矩陣，δA為加速度計標度因素重復性誤差，a表示各個測量軸方向上的視加速度輸入值。

根據慣組陀螺儀和加速度計指標數據，結合飛行器實際飛行過程中的角速度和視加速度最大值，按照上述計算公式，可以得到理論最大角速率偏差值和理論最大視加速度偏差值，再乘以緩變量故障判別增量計算時間即可得到緩變故障門限。

4 主從冗余故障診斷試驗驗證

主從冗余故障診斷試驗驗證主要通過在六自由度數學仿真環境中注入各種組合干擾、以及慣性器件可能存在的故障模式，模擬飛行器在實際飛行任務中的可能工作狀態，充分考核冗余診斷方案和冗余門限設計的合理性。最終，通過飛行試驗任務對冗余診斷方案和冗余門限進行檢驗。

以平臺倒臺故障測試為例，假設倒臺故障俯仰姿態角速度異常門限為15(°)/s，飛行器在100s開始平臺俯仰姿態角方向出現10(°)/s2的異常角加速度。俯仰姿態角速度曲線如圖4中實線所示，俯仰角速度勻速增大，有發生倒臺故障的趨勢，經濾波處理后，在101.74s附近判定平臺發生倒臺故障，切換到慣組飛行控制，此時俯仰姿態角約為17(°)/s。俯仰姿態角偏差曲線如圖4中虛線所示，雖然切換到慣組后姿態角偏差仍然逐漸增大至約13°，但很快收斂并最終趨近于0。試驗結果表明，倒臺故障診斷及冗余決策控制能夠有效避免平臺框架飛轉帶來的姿態發散，保障飛行器的穩定飛行。

圖4 倒臺故障模式下俯仰姿態角速度和俯仰姿態角偏差曲線

在某實際飛行試驗任務中，選取0～100s飛行時間段內的慣組加速度計緩變故障診斷過程數據如圖5所示，其中實線為慣組加速度計正交表與斜置表之間的一致性偏差數據曲線，最上面的段狀虛線為慣組加速度計緩變故障合理性門限上限，最下面的點狀虛線為慣組加速度計緩變故障合理性門限下限。由圖5可知，在實際飛行試驗條件下，慣組輸出未超過緩變故障門限，還有一定余量，慣組加速度計緩變故障診斷方案正確、門限設計合理。

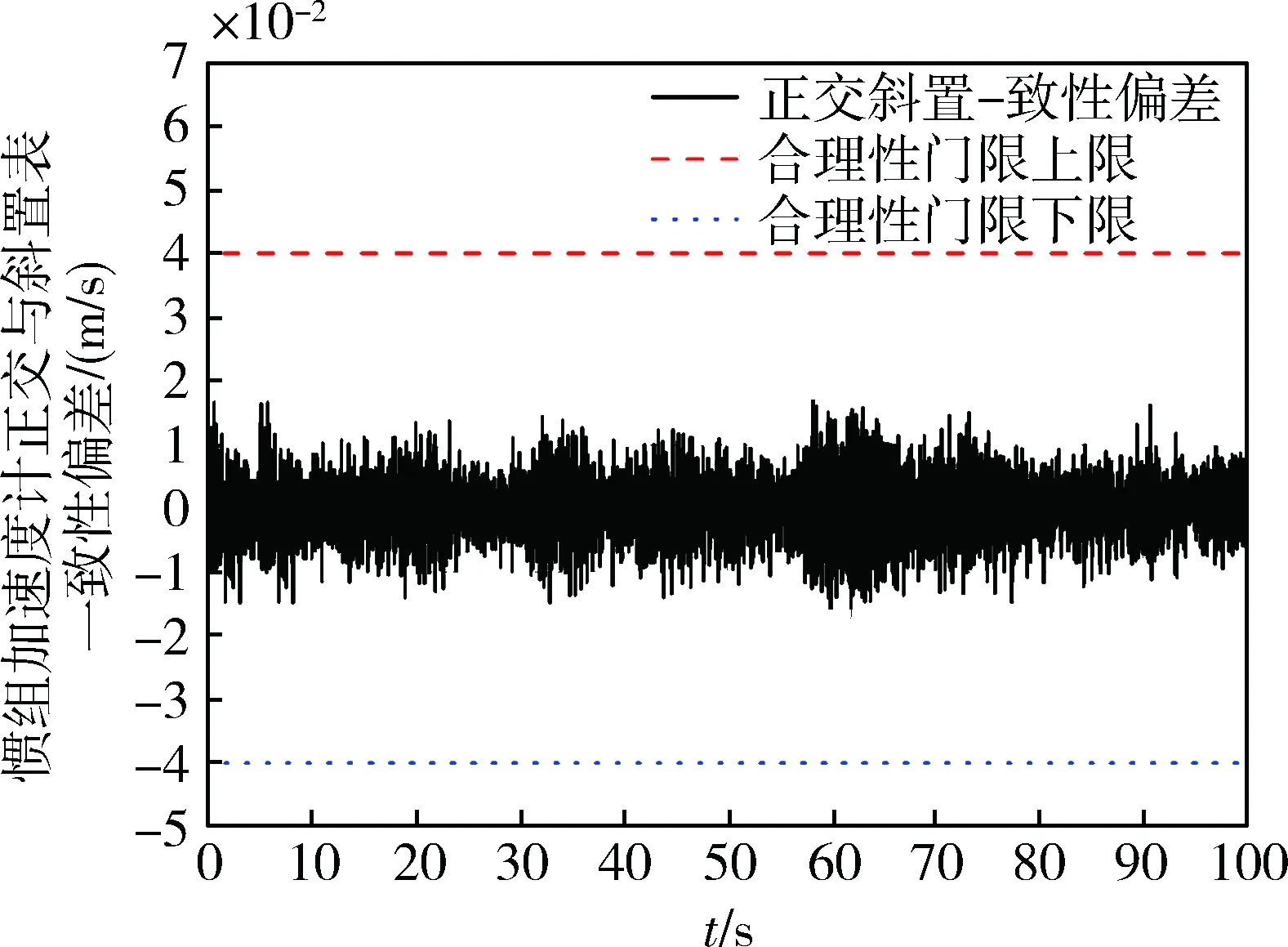
圖5 慣組加表緩變故障數據輸出曲線和門限比對

5 結論

針對非共面基座安裝的精度差異懸殊的平臺慣組的配置組合方式，提出了一種較優的冗余故障診斷及冗余決策方法，介紹了冗余門限設計的思路，通過了六自由度數學仿真試驗和飛行試驗的考核驗證。非共面基座的不對等精度平臺慣組主從冗余控制算法簡單可靠，故障診斷和重構能夠覆蓋全部一度故障，實際應用效果表明該方法合理可行。

[1] 徐延萬,余顯昭. 導彈與航天叢書-液體彈道導彈與火箭系列-控制系統(上)[M]．北京：宇航出版社，1989.(Xu Yanwan, Yu Xianzhao. Missile and Aerospace Series-Liquid Ballistic Missile and Rocket Series-Control System(Volume One) [M].Beijing: Aerospace Press,1989.)

[2] 肖利紅.平臺-捷聯冗余姿控系統設計[J].航天控制,2001,19(1)：31-54. (Xiao Lihong. Design of Attitude Control System of Platform-Strapdown Redundancy [J]. Aerospace Control,2001,19(1)：31-54.)

[3] 李伶. 雙捷聯冗余控制系統中的加速度計及陀螺儀判別方法研究 [J].航天控制,1998,16(2)：2-9. (Li Ling. Failure Detection for Accelemeter and Gyrometer in Double-Redundant Strapdown Control System [J]. Aerospace Control, 1998, 16 (2)：2-9. )

[4] 談學軍,洪剛,李建強,等. 雙捷聯冗余技術在長征二號丁運載火箭上的研發與實踐.[J].上海航天，2016,33(7):1-9.(Tan Xuejun,Hong Gang, Li Jianqiang, et al.Development and Implementation of Dual-Strapdown Inertial Redundant Technology in CZ-2D Launch Vehicle [J].Aerospace Shanghai,2016,33(7):1-9.)

[5] 李學鋒,張煥鑫. 運載火箭多表冗余捷聯慣組的故障診斷與決策[J].計算機測量與控制，2015, 23(7)：2241-2243.(Li Xuefeng, Zhang Huanxin. Fault Diagnosis and Decision-making for Launch Vehicle SIMU with Meters Redundancy [J].Computer Measurement & Control,2015,23(7):2241-2243.)

[6] 武唯強,陳康,閆杰.五冗余捷聯慣組最優配置設計[J]. 固體火箭技術,2015,38(1):18-22，29.(Wu Weiqiang, Chen Kang, Yan Jie.Optimal Configuration Design of Redundant Strapdown Inertial System with Five Axes [J].Journal of Solid Rocket Technology,2015,38(1):18-22.29.)

[7] 李學峰,王青,王輝，等．運載火箭飛行控制系統設計與驗證[M]．北京:國防工業出版社, 2014:56-60．(Li Xuefeng，Wang Qin，Wang Hui，et al．Design and Verification for Flight Control System of Launch Vehicle[M].Beijing :National Defend Industry Press，2014:56-60．)

[8] 沈鵬,張宏銘．基于小波分析的組合導航系統故障檢測方法研究[J]．儀器儀表學報,2009,30(10):80-82．(Shen Peng，Zhang Hongmin．The Research of Fault Detection Technique Based on Wavelet Analysis in Integrated Navigation System[J].Chinese Journal of Scientific Instrument,2009,30(10):80-82.)

[9] 張華強，趙剡，連遠峰．基于自適應概率神經網絡的SINS/GPS組合導航系統故障診斷方法[J]．中國慣性技術學報，2012，20(6):749-753．(Zhang Huaqiang，Zhao Yan，Lian Yuanfeng．Adaptive Probabilistic Neural Network Fault-diagnosis Algorithm for SINS/GPS Integrated Navigation System[J].Journal of Chinese Inertial Technology , 2012,20(6):749-753．)

[10] 田露，董云峰．基于UKF的陀螺故障預報方法[J]．航天控制，2014，32(3):76-80．(Tian Lu，Dong Yunfeng．Gyro Fault Prediction Algorithm Based on UKF[J]．Aerospace Control，2014，32(3):76-80．)

[11] 焦衛東，林樹森．整體改進的基于支持向量機的故障診斷方法[J]．儀器儀表學報，2015，36(8):1861-1870．(Jiao Weidong，Lin Shusen．Overall-improved Fault Diagnosis Approach Based on Support Vector Machine[J]．Chinese Journal of Scientific Instrument，2015,36(8): 1861-1870．)

[12] 王華，劉煥敏，段慧芬．基于案例推理方法在慣性導航故障診斷專家系統的應用[J]．中國慣性技術學報，2009，17(5):614-617．(Wang Hua, Liu Huanmin, Duan Huifen．Case-based Reasoning Method in Fault Diagnosis Expert System of Inertial Navigation System[J]．Journal of Chinese Inertial Technology , 2009, 17(5):614-617．)

[13] Shim D S,Yang C K.Geometric FDI Based on SVD for Redundant Inertial Sensor Systems[C]．The 5th Asian Control Conference，2004，2:1094-1100．

[14] Jin H,Zhang H Y.Optimal Parity Vector Sensitive to Designated Sensor Fault[J]．IEEE Transactions on Aerospace and Electronic Systems, 1999,35(4):1122-1128．