測量船平臺慣導設備陀螺故障快速定位方法研究*

程 龍 姜永剛 朱棟山 孫海躍

中國衛星海上測控部，江陰 214431

測量船海上測量是在動態條件下進行的，設備的位置和姿態在不停地變化，必須在測量設備跟蹤被測目標的同時，對船的姿態位置進行同步測量，將測量設備的測量數據經船姿船位修正，變成地心固聯坐標系內的數據，才能與整個試驗區建立起聯系[1]。所以船姿船位測量是海上測量的關鍵點。慣性導航設備(INS)是目前航天測量船的核心導航設備，其在載人航天飛船、飛船與空間站對接、探月工程等任務測量精度中具有重要意義。

INS能夠連續提供載體位置、速度、姿態，廣泛應用于各種載體的運動狀態測量，成為制導的主要手段。其特點為：1)依靠自身測量載體運動，是一種完全自主式導航系統；2)不發射和接收信號，不存在電磁波傳播問題，不受外界環境、條件及其它因素的影響；3)機動靈活，輸出結果穩定、連續，系統裝在載體上，不存在導航定位盲區；4)能夠提供定位、測速、姿態測量與控制信息等全面的導航參數[2]。INS/GPS組合導航系統是測量船船姿船位測量的主要設備。INS姿態測量的核心測量元件陀螺儀屬于高精密器件，一旦出現故障會直接導致設備無法正常輸出高精度的測量結果。當INS出現異常將直接導致輸出結果無法滿足任務要求，因此快速定位并排查故障顯得尤為重要，本文基于多起陀螺故障排查經驗和對設備原理的分析給出快速定位陀螺故障的方法。

1 陀螺儀及慣性導航系統跟蹤地理坐標系原理

INS測量感受到作用力或力矩，利用牛頓運動定律積分得到船舶的速度、位置和姿態信息。船舶測量加速度的元件為加速度計，而測量角加速度的元件是陀螺儀。在傳統工程技術中，高速旋轉的轉子裝在相應的框架上組成了陀螺儀，其基本特性主要有定軸性和進動性。在現代技術中，具有陀螺測角效應的元件均為陀螺儀。

1.1 陀螺儀

1.1.1 定軸性

在沒有外力矩作用下，裝在運動載體上的陀螺儀，不管載體如何運動，陀螺儀自轉軸相對慣性空間的初始方位始終保持不變，這稱為陀螺儀的定軸性。

在干擾力矩作用下，陀螺儀的自轉軸偏離初始方位，自轉軸在單位時間內的方位變化稱為漂移率，這是衡量陀螺儀性能的一個最重要指標，通常以“(°)/h”或“rad/s”來表示。干擾力矩可來自框架軸承的摩擦力、陀螺轉子的質心與框架支承中心不重合產生的靜不平衡力矩、以及由運動物體加速度引起的慣性力矩等。

1.1.2 進動性

高速度旋轉的陀螺自轉軸在其受到垂直于它的外力矩M作用時，將向垂直于外力矩和自轉軸的方向作勻速轉動。這種轉動稱為陀螺儀的進動。

M=ω×H

(1)

H為陀螺轉子的角動量(即動量矩)，ω為進動角速度。

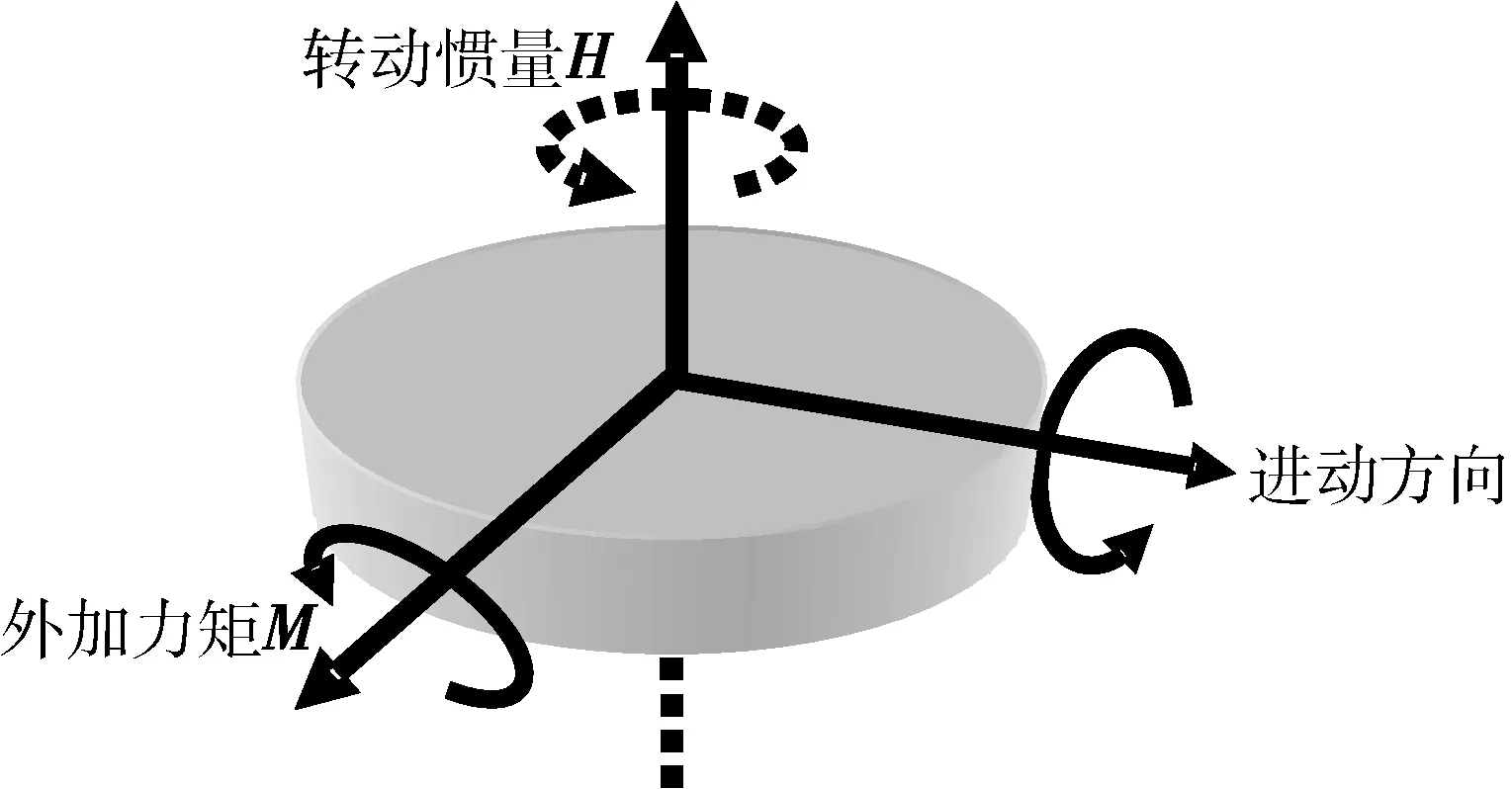
圖1 陀螺儀的進動、外力矩、自轉軸的方向關系示意圖

1.2 慣性導航系統跟蹤地理坐標系原理

由于地球自轉和測量船相對地球的運動，地理坐標系各軸相對慣性空間的指北是不斷變化的。地理坐標系相對慣性空間旋轉角速度在地理坐標系軸向分量分別為ωx，ωy，ωz，即：

(2)

Vx，Vy分別為東向和北向速度，RM，RN分別為地球子午圈曲率半徑和卯酉圈曲率半徑，La為船舶所在緯度，Ω為地球自轉角速度[3]。

利用陀螺儀的進動特性，在輸出軸上加控制力矩可以控制陀螺自轉軸的運動，使主軸指向需要的方位，達到跟蹤地理坐標系的目的。此控制慣性元件跟蹤地理坐標系的系統稱之為修正回路。整個系統有東向、北向、方位這3條修正回路。當系統受到外力矩作用時，陀螺敏感輸入作用力矩而產生輸出，一方面用于控制慣性元器件定向于東北天坐標系，另一方面輸出船舶姿態角。同樣，系統有橫搖、縱搖和艏搖這3條控制回路。

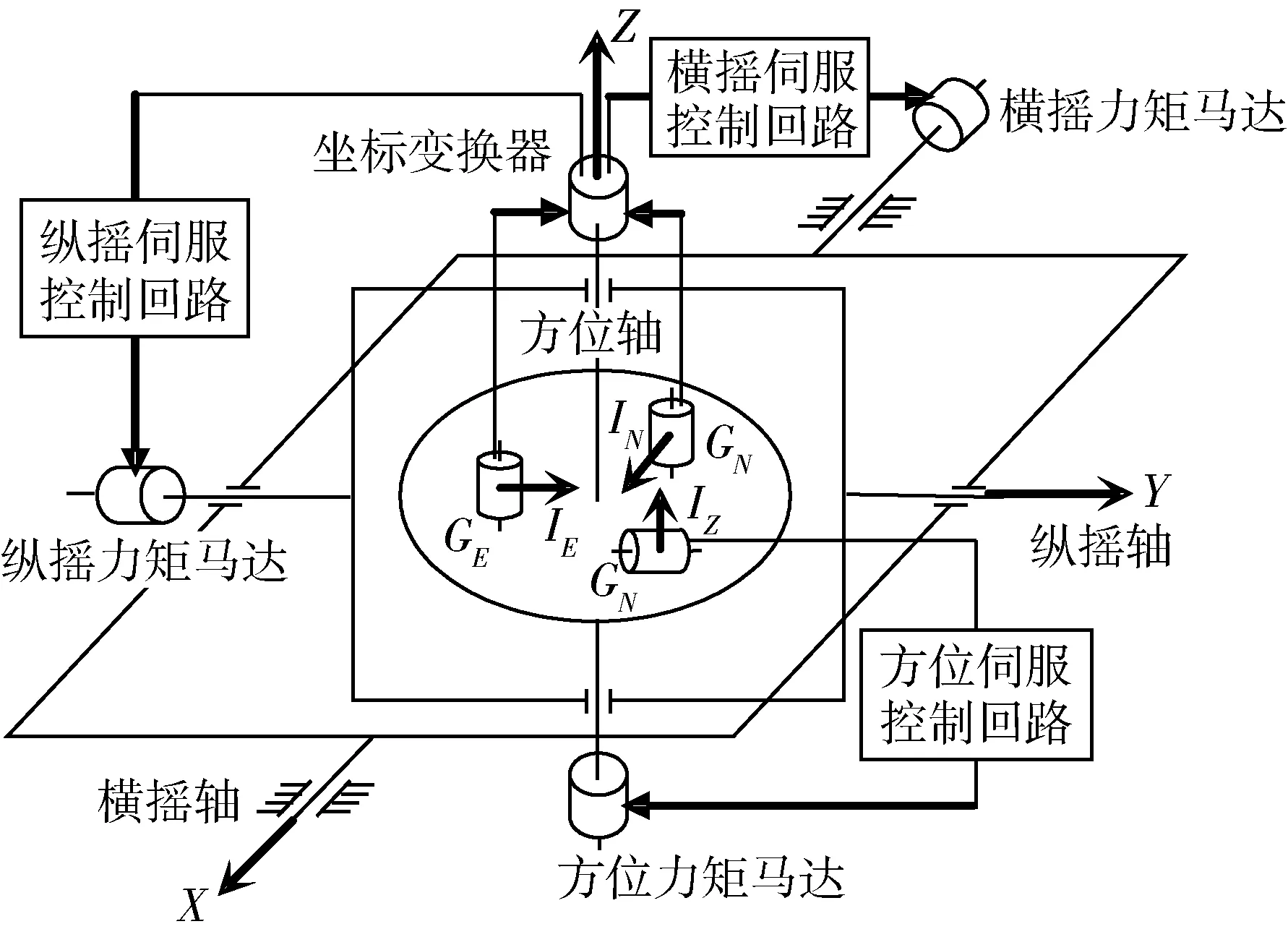
圖2 三軸穩定平臺結構示意圖

測量船目前主要使用天津航海儀器研究所研制的慣性導航設備，其陀螺儀為液浮式單自由度積分陀螺儀。其優點為動態范圍大、測量精度高、可靠性高、體積小和壽命長。而其最大的缺點為價格高昂。

2 陀螺性能對輸出結果的影響

平臺漂移的大小是判斷慣性導航系統精度的關鍵指標之一，而導致平臺漂移有諸多因素，例如陀螺漂移εg(s)、陀螺輸出通道交叉耦合δωθ(s)、干擾力矩δωM(s)、基座角運動δωB(s)、振動誘導漂移δωT(s)和圓錐效應漂移δωα(s)等[4]。陀螺儀作為慣導設備的測量元件，其穩定性直接決定了輸出結果，當其出現故障時，往往無法直觀地從結果判斷出來。

根據慣性導航原理，東向陀螺與北向加速度計及其線路構成北向加速度計回路，北向陀螺與東向加速度計及其線路構成東向加速度計回路，3個陀螺與相應的力矩馬達、控制線路構成三路伺服控制回路。當回路的參數進行舒拉調諧之后，導航參數也具有舒拉周期的振蕩，而考慮3個通道的相互耦合，導航參數振蕩也將有傅科周期和地球周期的振蕩特性。根據半解析式慣性導航系統的動力學方程，平臺輸出姿態誤差方程為[5-6]:

(3)

式中，ΔVx,ΔVy,ΔLa,φx,φy,φz,La,Vx,Vy,Ω,RN,RM,εx,εy,εz,分別表示東向速度誤差、北向速度誤差、系統緯度誤差、東向姿態角、北向姿態角、方位姿態角、緯度、東向速度、北向速度、地球自轉速度、地球子午圈半徑、地球卯酉圈半徑、東向陀螺漂移、北向陀螺漂移和方位陀螺漂移。該方程的推導及解析解可參閱文獻[5]。

速度誤差由導航參數誤差、平臺姿態誤差引起的重力偏量、加速度計零偏引起，位置誤差主要由北向、東向速度誤差及緯度誤差引起，其關系式可參閱文獻[4]。由此可見，平臺誤差將會導致慣性導航系統導航參數的偏差，而陀螺漂移是平臺短期誤差的主要誤差源。由于水平姿態角的變化由坐標變換器輸出為橫縱搖角，其誤差變化并不明顯，所以往往難以從結果現象來快速定位故障部位。取Δεx，Δεy和Δεz為慣性導航系統東向、北向及方位陀螺的隨機漂移率，它們是長期航行的慣性導航系統導航信息的主要誤差源，需要通過GPS位置數據校準來判讀誤差[2,6-9]。系統工作在正常導航狀態時，認為陀螺標度因素是完全準確的，此時系統速度誤差方程可通過取2個時間點來判斷其由隨機漂移引起的誤差[10]。東向速度誤差ΔVx主要由北向陀螺、東向加速度計及其相關線路產生，一般加速度計故障引起的速度誤差變化規律不明顯，而北向陀螺漂移異常的同時會出現航向誤差[11]，在加速度計正常情況下東向速度誤差ΔVx與北向陀螺儀隨機漂移Δεy、航向誤差ΔH的關系式為：

ΔVx≈-ΔεyR+ΔHΩRsinLa

(4)

R為球形地球半徑，La為船舶所在緯度，Ω為地球自轉角速度。

北向速度誤差ΔVy主要由東向陀螺、北向加速度計及其相關線路產生，同理，在加速度計正常的情況下，北向速度誤差ΔVy與東向陀螺儀隨機漂移Δεx、航向誤差ΔH的關系式為：

ΔVy≈ΔεxR-ΔHΩRcosLa

(5)

當認為初始北向速度誤差ΔVy0=0時，初始航向誤差ΔH0由東向陀螺儀隨機漂移Δεx產生

(6)

當初始校正結束或經過GPS校正后，在短期內不考慮東向陀螺儀隨機漂移誤差的影響，則系統中航向誤差ΔH的變化可由式(7)表示：

(7)

橫搖角差ΔR和縱搖角差ΔP統稱為水平姿態誤差受船舶航向變化影響，其變化并不明顯。

3 測量結果快速反推陀螺隨機漂移方法

海上應急校初始航向誤差ΔH0由東向陀螺儀隨機漂移Δεx，所以東向陀螺儀隨機漂移

Δεx≈ΔH0ΩcosLa

(8)

當系統已處于導航狀態時，東向陀螺儀隨機漂移Δεx會引起航向誤差ΔH和北向速度誤差ΔVy，故東向陀螺漂移為

(9)

根據式(4)反推北向陀螺儀隨機漂移有

(10)

因北向陀螺引起的航差并不及其他陀螺明顯，而東向速度誤差是其主要表現特征，因此有北向陀螺儀隨機漂移

(11)

當北向陀螺漂移穩定時，由式(7)可以反推出方位陀螺儀隨機漂移

(12)

在有其他導航手段的情況下，可觀察到異常INS姿態的變化，采用GPS位置及速度與INS比較，可直觀觀察到位置誤差和速度誤差的變化[2,6,11]。INS本身只能解決由航向差估計陀螺隨機漂移，不能解決位置速度誤差隨時間發散的問題[8]。

4 案例分析

根據前述方法，在某測量船分析定位多起陀螺故障，均實現快速定位故障，及時采取對策，確保系統高精度的輸出結果。

4.1 東向陀螺儀故障

2013年某日，船舶處于北緯某緯度碼頭，慣導系統應急校轉20后，監控軟件顯示北向速度誤差快速增加至-40kn，對陀螺補償較大漂移后仍有較大誤差，如圖3所示。根據式(9)可得東向陀螺漂移結果如圖4所示。

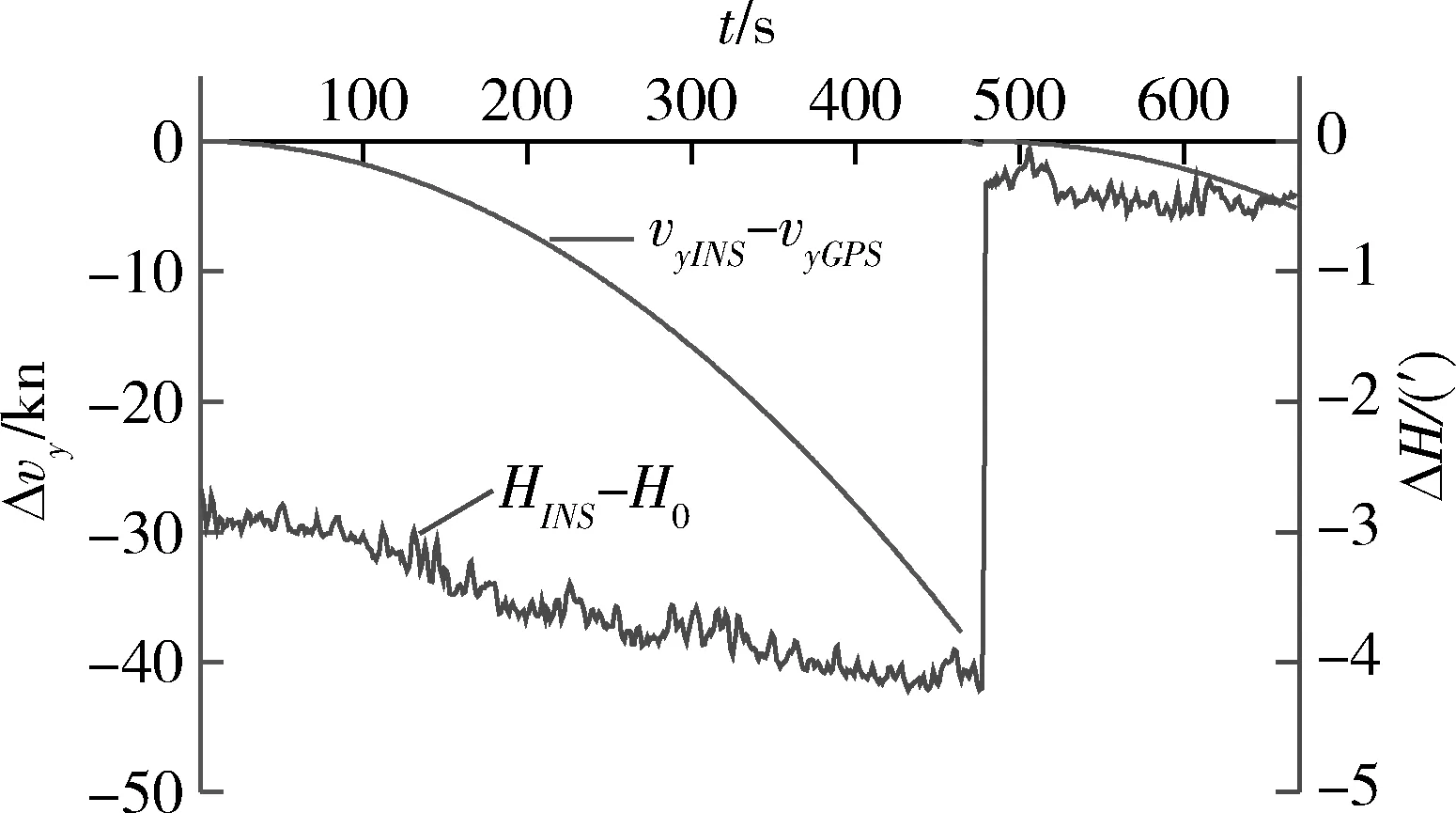
圖3 與GPS北向速度的差值隨時間變化

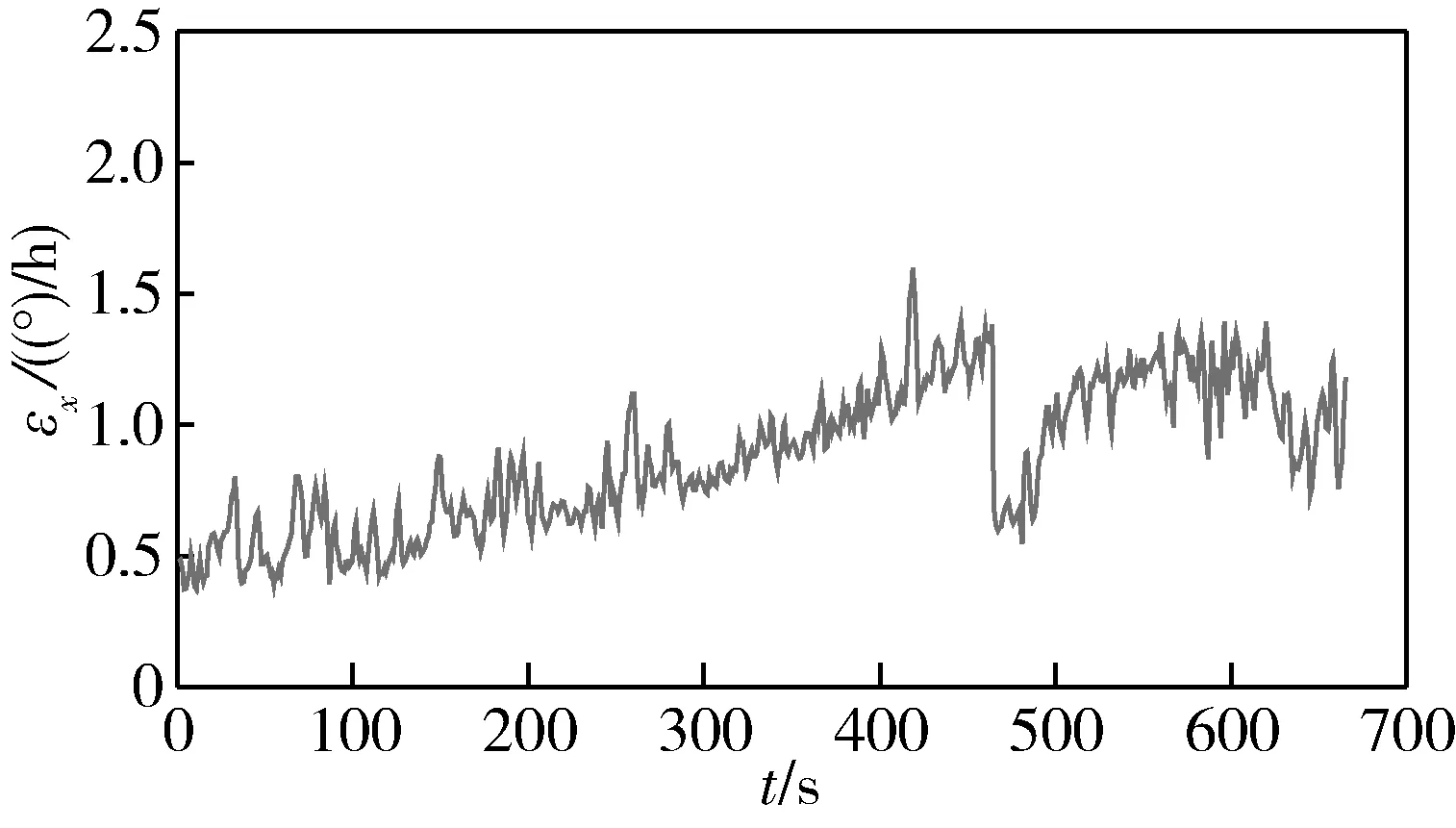
圖4 計算得到的東向陀螺漂移

重啟后系統正常對準長期處于東向陀螺儀測漂移階段。圖5所示為故障INS在正常對準測量的東向陀螺儀漂移，可以看出陀螺漂移在1(°)/h附近，并不斷增大，其走勢與計算結果相吻合。

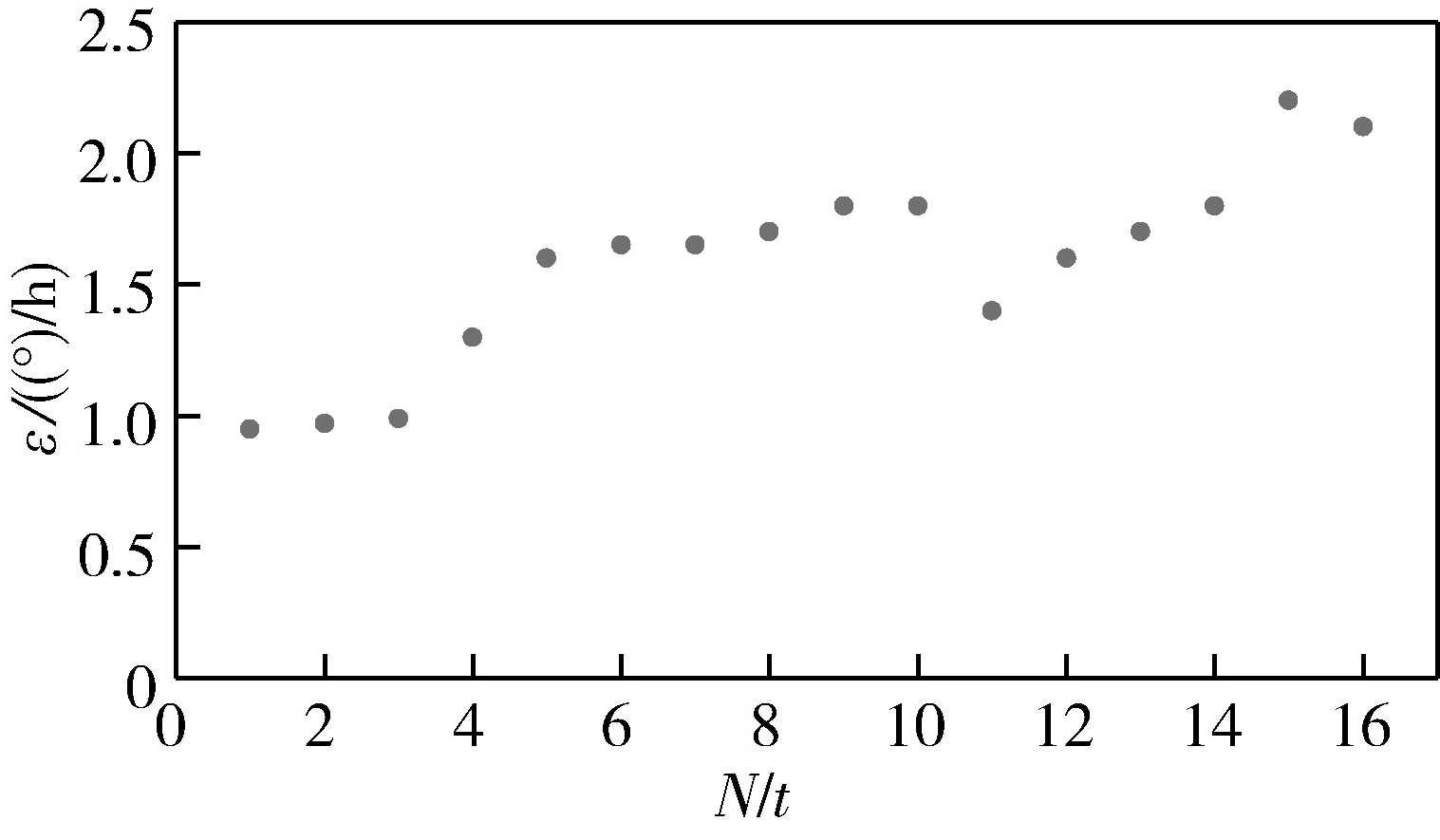
圖5 正常對準階段東向陀螺儀漂移

重新啟動應急對準，重復出現北速誤差迅速變大現象。依據式(5)可知北向速度誤差由航向誤差和東向陀螺儀漂移引起，當航向異常且速度變現變化時可斷定東向陀螺儀出現異常。

該故障現象在更換東向陀螺儀后排除，最終經廠所鑒定故障定位為東向陀螺儀力矩電機性能下降。

4.2 北向陀螺儀故障

2015年某日，船舶處于南緯低緯度海域，慣性導航系統與GPS東向速度誤差在30min內快速增加至37kn，如圖6所示。

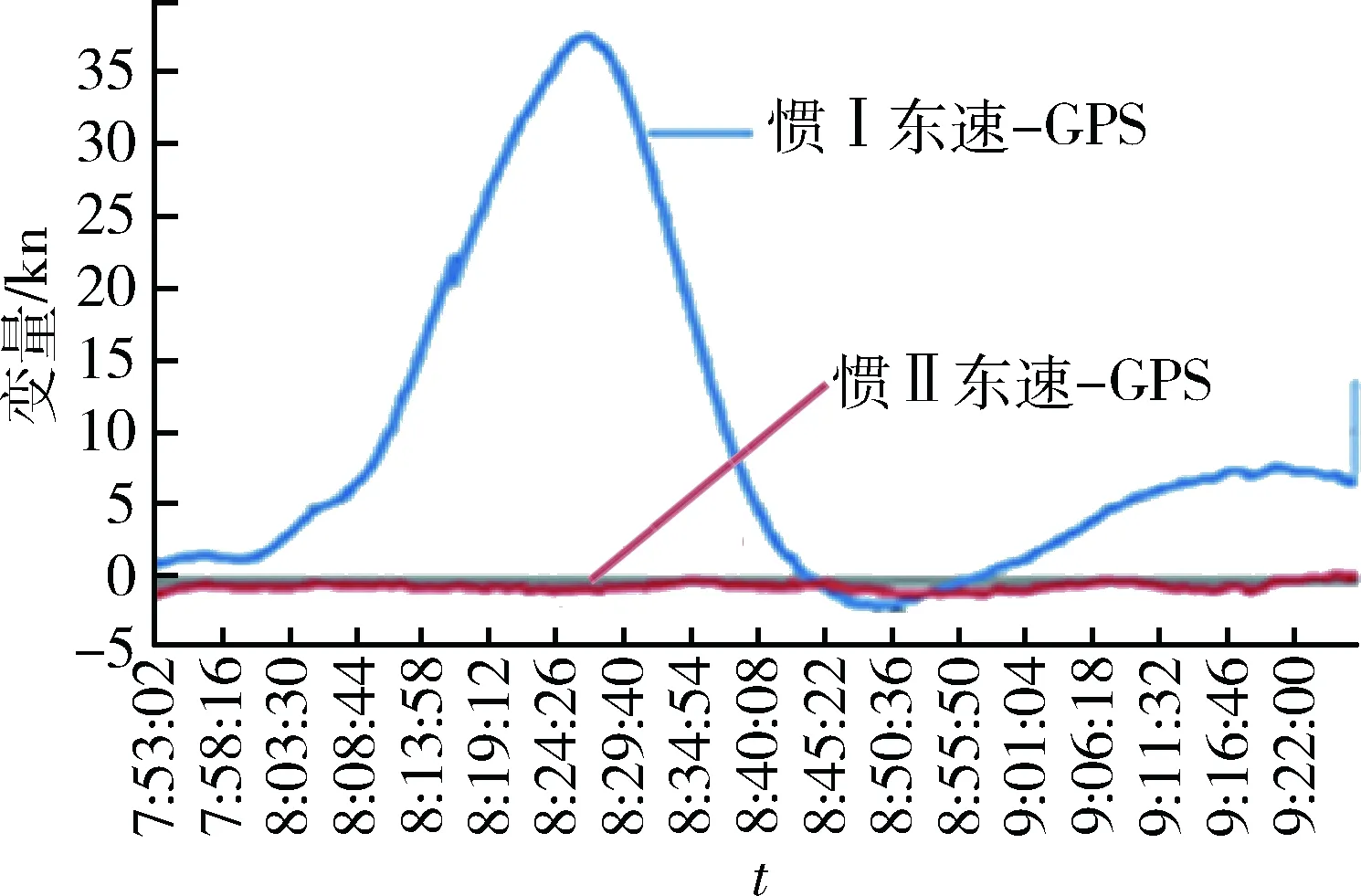
圖6 與GPS東向速度的差值隨時間變化

綜校時系統與GPS比較經度差為3.8′，北向陀螺漂移達-0.0412(°)/h。在此過程中船舶航向，橫搖角均出現較大誤差擾動，如圖7。重啟設備后，系統自解算北向陀螺漂移較大，東向速度誤差一直較大，系統不穩定。

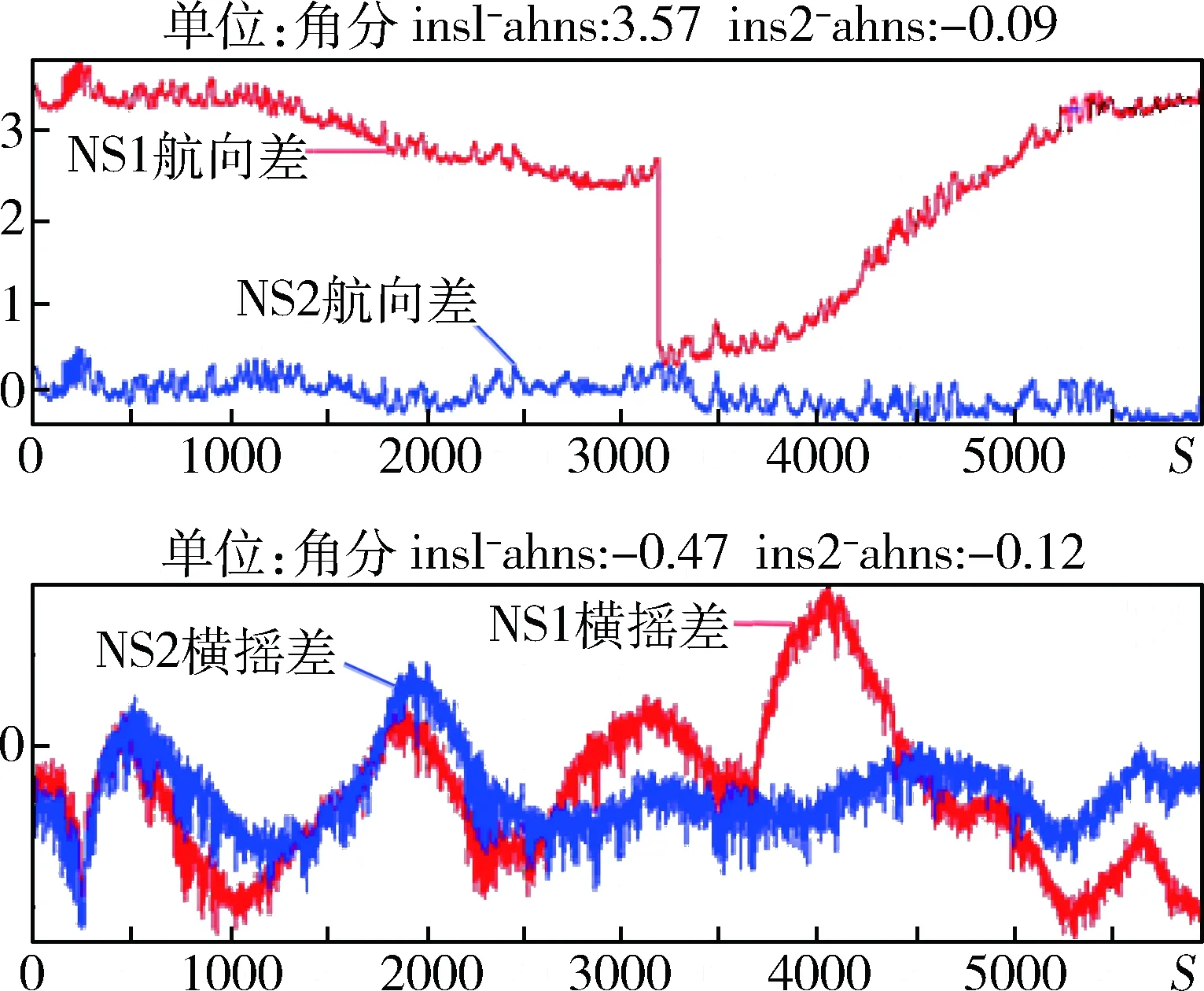
圖7 與捷聯慣導相比2套慣導姿態角誤差

利用式(11)可以判斷為北向陀螺異常，陀螺漂移最大達到-0.6(°)/h。更換北向陀螺儀后故障排除，最終經廠所鑒定故障定位為北向陀螺儀性能下降，陀螺漂移不穩定。

4.3 方位陀螺儀故障

2015年某日，船舶處于赤道附近，慣性導航系統出現航向誤差變化較大且無規律的情況，如圖8所示，通過校準方位陀螺漂移無法使系統穩定，打印顯示方位陀螺累積漂移-0.1350(°)/h，東向陀螺累積漂移較小，整個過程橫搖差、縱搖差均正常。根據式(12)可給出方位陀螺隨機漂移變化曲線(圖9)，重啟方位陀螺無法啟動力矩馬達，有陀螺啟動用三相電源故障或陀螺故障，測量水平陀螺啟動電壓正常，方位陀螺供電模塊不能正常按流程啟動。

圖8 慣導姿態角誤差變化曲線

圖9 方位陀螺隨機漂移曲線

更換方位陀螺儀后故障排除，最終經廠所鑒定故障定位為方位陀螺儀力矩器故障。

5 結論與展望

一般船載INS長時間連續工作時，若元器件突然發生輸出故障，往往不能直接判斷故障位置，因此，無法給出故障碼。通常情況下需要工作人員連續觀察數據變化情況，通過不同類型的輸出數據的變化來確定定位故障位置。單獨的一套INS設備在沒有其他輔助導航設備情況下無法判斷設備異常，在有多套設備、衛星導航、重力輔助、捷聯慣導及經緯儀等其他高精度導航設備的組合導航系統中可以通過分析數據來定位故障設備。在此，衛星導航(包含GPS，GLONASS，BD)因具有穩定性、較高的定位精度在速度變化，位置誤差分析中有重要作用。經緯儀用于水面船舶較為便捷且航向定位精度高。某測量船載導航系統包含了衛星導航、經緯儀和雙套INS設備，因此,首先采取慣性導航設備自身的GPS位置校準和人工輸入帶航向差的位置校準直接對系統誤差進行校準，并對相關陀螺漂移修正量進行分析。在設備依然無法輸出滿足精度的結果時進一步進行關機檢查相關控制信號、重啟系統觀察數據，最后再考慮陀螺等核心元件的更換。

通過分析元器件誤差對輸出結果的影響，并結合某測量船多起故障的現象分析，給出一些陀螺儀故障定位的常用方法。通過該方法可有效縮短陀螺故障排查時間，提高設備參試能力，該方法可能在一些特殊奇點存在較大誤差，在設備故障排查中應根據實際情況進行綜合判斷。

[1] 潘良. 船姿船位測量技術[M]. 北京：國防工業出版社，2009.(Pan L. The Ship Posture and Position Measurement Technology[M]. Beijing: National Defence Industry Press, 2009.)

[2] Hong S, Lee M H, Chun H H, et al. Observability of Error States in GPS/INS Integration[J]. IEEE Transactions on Vehicular Technology, 2005, 54(2): 731-743.

[3] 鄧正隆. 慣性技術[M]. 哈爾濱：哈爾濱工業大學出版社, 2006.(Deng Z L. Inertial Technology[M]. Harbin: Harbin Industrial University Press, 2006.)

[4] 秦永元.慣性導航[M]. 北京：科學出版社, 2006. (Qin Y Y. Inertial Navigation[M]. Beijing: Science Press, 2006.)

[5] 慣性導航系統編著小組. 慣性導航系統[M]. 北京：國防工業出版社, 1982. (The Group of INS. Inertial Navigation System[M]. Beijing: National Defence Industry Press, 1982.)

[6] Farrell J A, Givargis T D, Barth M J. Real-time Differential Carrier Phase GPS-aided INS[J]. IEEE Transactions on Control Systems Technology, 2000, 8(4): 709-721.

[7] 張忠華. 航天測量船船姿船位數據處理方法[M]. 北京：國防工業出版社，2009.(Zhang Z H. Method of Space Surveillance Ship Posture and Position Data Processing[M]. Beijing: National Defence Industry Press, 2009.)

[8] Han S, Yuan B, Lu G, et al. The Development and Evaluation of a Two-axis Indexing NFFDLG INS for Marine Navigation[C]//2015 DGON Inertial Sensors and Systems Symposium (ISS). IEEE, 2015: 1-16.

[9] 韓鵬鑫，穆榮軍，崔乃剛.兩種坐標系下慣導傳遞對準效果比較[J]. 中國慣性技術學報,2010, 18(3): 272-278.(Han P X, Mu R J, Cui N G. Comparison Between Transfer Alignments of Inertial Navigation System in Two Coordinates[J]. Journal of Chinese Inertial Technology, 2010, 18 (3) : 272-278.)

[10] Gu S, Zeng Q, Liu J, et al. FOG De-noising Method Based on Empirical Mode Decomposition and Allan Variance[C]. China Satellite Navigation Conference (CSNC) 2016 Proceedings: Volume I. Springer Singapore, 2016: 299-308.

[11] 周峰，孟秀云. 基于自適應UKF算法的機載INS/GPS空中對準研究[J].系統工程與電子技術, 2010, 32(02): 367-371.(Zhou F, Meng X Y. In-flight Alignment Research for Airborne INS/GPS Based on Adaptive Unscented Kalman Filter Algorithm[J]. Journal of Systems Engineering and Electronics, 2010, 32(02): 367-371.)