發(fā)現關聯遞進解題

☉江蘇東臺市實驗中學教育集團 崔恒劉

發(fā)現關聯遞進解題

☉江蘇東臺市實驗中學教育集團 崔恒劉

牛頓從蘋果砸頭的情景中發(fā)現萬有引力，瓦特從開水壺嘴噴氣的情景中發(fā)明蒸汽機……任何發(fā)現、發(fā)明離不開必要的情景，因此新課程標準提倡探究性學習，要求在新知識的學習過程中，先創(chuàng)設必要的情景，再引導學生觀察、猜想，不斷嘗試，以期從中發(fā)現規(guī)律并應用規(guī)律解決問題.體現在近幾年的中考壓軸題中，出現了“分析試題提供的信息和內部的結構特點，發(fā)現并利用其隱含的關聯效應解題”的新趨勢.本文以2016年淮安市中考試題第28題為例說明這類考題的應對策略.

一、中考真題

問題背景：

如圖1，在四邊形ADBC中，∠ACB=∠ADB=90°，AD= BD，探究線段AC、BC、CD之間的數量關系.

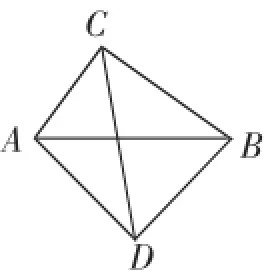
圖1

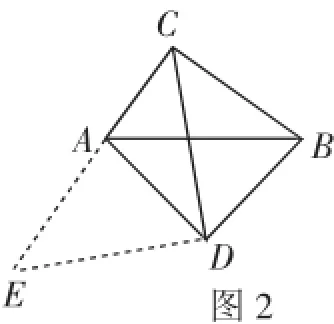
圖2

小吳同學探究此問題的思路是：將△BCD繞點D逆時針旋轉90°到△AED處，點B、C分別落在點A、E處（如圖2），易證點C、A、E在同一條直線上，并且△CDE是等腰直角三角形，所以從而得出結論：AC+ B

簡單應用：

（2）如圖3，AB是⊙O的直徑，點C、D在⊙O上，弧AD=弧BD，若AB=13，BC=12，求CD的長.

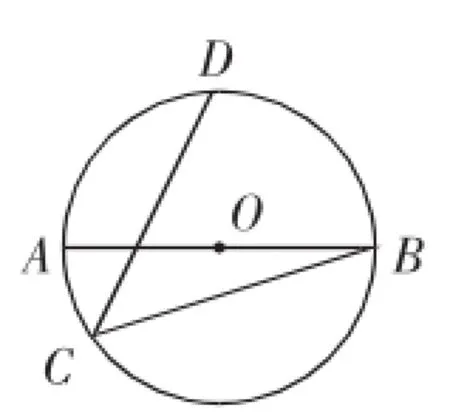
圖3

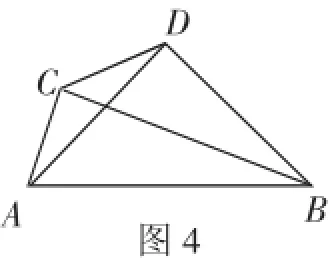
圖4

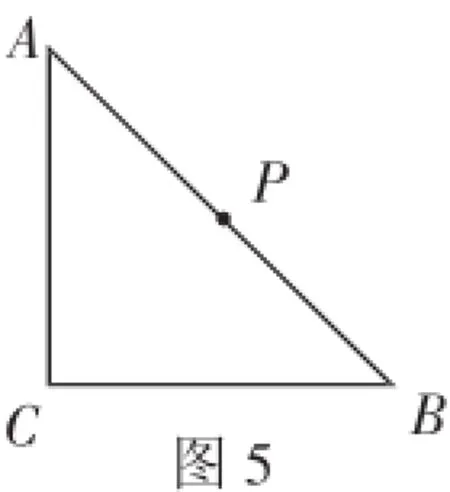
圖5

拓展規(guī)律：

（3）如圖4，∠ACB=∠ADB=90°，AD=BD，若AC=m，BC=n（m＜n），求CD的長（用含m、n的代數式表示）.

（4）如圖5，∠ACB=90°，AC=BC，點P為AB的中點，若點E滿足AE=C，CE=CA，點Q為AE的中點，則線段PQ與AC的數量關系是________.

二、思路探究

首先要讀懂問題背景提供的模型：四邊形由有公共斜邊的兩個直角三角形組成（公共斜邊的兩側），其中一個是等腰直角三角形，則另一個直角三角形的兩直角邊之和等于四邊形兩個直角頂點之間距離的

第（1）問是熱身，它把背景問題數量化，只要將給出的AC與BC的長度值代入問題背景提供的結論AC+BC=，即可得出CD的長度，屬于送分題.

解答（2），勿忘（1），第（2）問改變了問題的情景，將直線型的圖形放置在圓中，由于已知AB為⊙O的直徑，且弧AD=弧BD，則必然會想到圓的相關性質：直徑所對圓周角為直角，同圓中等弧所對弦相等，由此提示我們連接AC、BD、AD，便有了問題背景提供的模型“有公共斜邊的兩個直角三角形組成（公共斜邊的兩側）的四邊形，其中一個是等腰直角三角形”，利用問題背景所給出的證明思路即可求出CD的長度；牢記問題背景提供的模型真的好解題.

第（3）問與問題背景不同的是：由在斜邊兩側的兩個直角三角形變?yōu)榱嗽谕瑐鹊膬蓚€直角三角形，怎么辦？轉化，構造背景提供的模型，然后利用問題背景提供的模型求解.第（2）問中多了個圓，試試作以AB為直徑的⊙O，如圖6，圓是軸對稱圖形，因此把△ABD沿直線AB翻折，又有了問題背景提供的模型，由此可求CD1，D1D是直徑，所以利用勾股定理即可求出CD的長度.

第（4）問，題圖簡單，問題是圖沒畫全，要我們自己畫圖，肯定有文章，原來點E的位置有兩種，一是點E在直線AC的右側，二是點E在直線AC的左側.分別畫出圖7、8，下面的事就是嘗試構造問題背景中的模型.等腰、中點，連接CQ、CP后，問題背景中的模型便有了.

三、試題解答

（1）由問題背景提供的信息，可知：AC+BC=■：2CD.

將AC與BC的長度值代入：

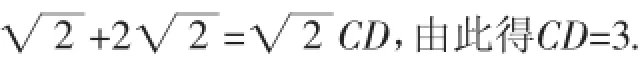
（2）連接AC、BD、AD.

在⊙O中，由AB是⊙O的直徑，得∠ADB=∠ACB= 90°.又AB=13，BC=12，則AC=5.

由弧AD=弧BD，得AD=BD.

由于∠ACB=∠ADB=90°，所以OA=OB=OC=OD，所以A、C、D、B四點都在⊙O上.連接DO并延長交⊙O于點D1，連接D1A、D1B、D1C，則∠AD1B=90°.由AD=BD，得AD1= BD1，如圖6.

由D1D是⊙O的直徑，得∠DCD1=90°.

在Rt△ABC中，由勾股定理，得AB2=AC2+BC2=m2+n2.

在Rt△DCD1中，由勾股定理，得DD12=CD12+CD2.

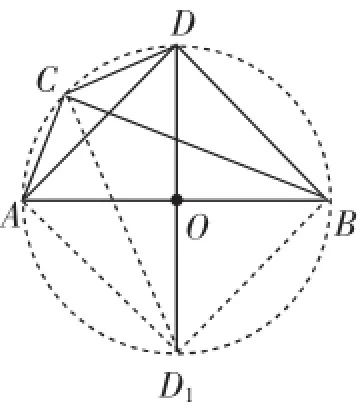
圖6

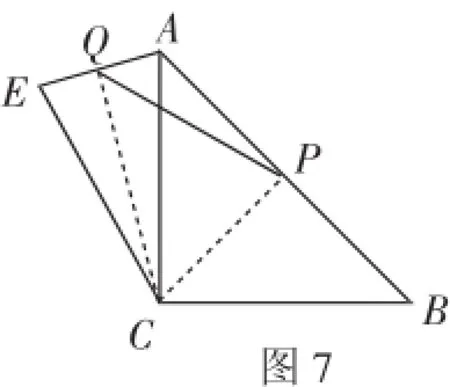
圖7

（4）當點E在直線AC的左側時，如圖7，連接CQ、PC.

由AC=BC，∠ACB=90°，點P是AB的中點，得AP=CP，∠APC=90°.

由CA=CE，點Q是AE的中點，得∠CQA=90°.

當點E在直線AC的右側時，如圖8，連接CQ、CP.

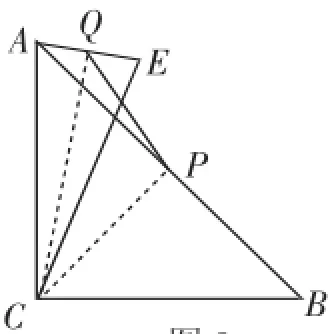
圖8

同理可知：∠AQC=∠APC=90°.

設AC=a.

四、教學反思

布魯納說：“學習不但應該把我們帶往某處，而且還應該讓我們日后的繼續(xù)前進更容易.”波利亞指出的：“在解題的每一階段……我們都要用已經得到的知識去得出更多知識.我們要靠逐省逐省的占領去最后征服一個王國.在每個階段，我們利用已被征服的省份作為行動基地去征服下一個省份.”本題提供問題背景，讓學生在閱讀理解的過程中，掌握一個基本模型，再在簡單應用環(huán)節(jié)中，用問題（1）讓學生直接套用基本模型以進一步熟悉模型，設計問題（2）讓學生應用所學知識構建基本模型解決問題，以加深理解基本模型；問題（2）比問題（1）進了一步；在拓展規(guī)律環(huán)節(jié)中，對基本模型進行變化，將兩個直角三角形在公共斜邊的兩側變?yōu)橥瑐仍O計問題（3），引導學生深入研究問題，要想順利解答問題（3），必須回到基本模型中，深入理解基本模型的研究思路，尋找變化后的問題與基本模型之間的關系，有效地化歸問題；問題（4）則體現了基本模型的應用價值，題中畫圖留白，提醒學生注意分類研究.四個問題，每一問都緊扣著前一問，運用規(guī)律、層層遞進、創(chuàng)新探究，體驗數學的建模思想和應用價值，對學生的創(chuàng)新思維進行考查，有利于開展研究性學習，實現數學的人文教育功能.

遞進式的綜合探究題，編制上往往有一個特點，就是問題設計層層深入，后一個問題的解答或者直接應用上一個問題的結論，或者類比上一個問題的研究思路方法.表現在能力層次上的要求為：模仿→構建→運用.解題的應對策略是：首先，要理解題目提供的問題背景，即基本模型，只有在理解了基本模型的基礎上才能運用基本模型；其次，探尋問題與基本模型之間的關系，將要解決的問題轉化為基本問題.化歸思想在數學中幾乎無處不在，它是數學教學中最基本的思想方法，在遞進式的綜合探究題中顯得特別搶眼.

數學解題是一個不斷地將未知轉化為已知，由不熟悉轉化為熟悉的過程，命題者在命題時會鋪設臺階，一步一步提升難度.在解題時，我們要將題中的條件與問題聯系起來觀察、比較、聯想，從而發(fā)現題目內部的關聯、遞進關系，洞察命題者發(fā)出的暗語：層層誘導，先通過特殊情形認識問題，再進一步解決特殊化的數學問題，最后利用上述形成的結論或方法，來解決后面的數學問題，最終順利解決問題.近年來，中考數學壓軸題特別重視突出數學思想和方法的考查.因此，在平時的教學中，要注意體會、歸納教材、題目中的數學思想方法.尤其在中考復習時，教師更應有意識、有目的、適時地滲透數學思想方法，從解題過程中獲取解題經驗，感受解題過程中的思維體驗，培養(yǎng)學生有效利用數學思想方法解決相關問題的能力.

1.波利亞：數學的發(fā)現［M］，呼和浩特：內蒙古人民出版社，1982.