以退為進：挑戰新定義考題的有效策略
——北京海淀九上期末卷第29題解析與賞析

☉廣西南寧市第二中學 甘曉云

以退為進：挑戰新定義考題的有效策略
——北京海淀九上期末卷第29題解析與賞析

☉廣西南寧市第二中學 甘曉云

近年來，有命題興趣的同行都會關注和研究北京市各區的期末試卷，因為北京市各區的期末試卷往往都有很多原創的特色試題，這些試題貼近北京市中考題風格，很有數學味道，值得思考.本文賞析北京海淀區九上期末卷第29題，并跟進命題思考，供研討.

一、考題解析與回顧反思

考題（2016～2017學年九上期末試卷，第29題）定義：點P為△ABC內部或邊上的點，若滿足△PAB、△PBC、△PAC中至少有一個三角形與△ABC相似（點P不與△ABC的頂點重合），則稱點P為△ABC的自相似點.

例如：如圖1，點P在△ABC的內部，∠PBC=∠A，∠PCB=∠ABC，則△BCP∽△ABC，故點P為△ABC的自相似點.

在平面直角坐標系xOy中，

圖1

圖2

圖3

②若k=2，點N的坐標為（2，0），且△MON的自相似點有2個，則曲線C上滿足這樣條件的點M共有_____個，請在圖3中畫出這些點（保留必要的畫圖痕跡）.

思路突破：

（1）只要構圖連接OF、BF，結合F點的坐標，可確認∠OFB為90°，且∠FOB=30°，于是點F是△AOB的自相似點；再構圖聯系BG，會確認BG⊥AO，故G也是△AOB的自相似點.

（2）直接求解兩問比較困難，找不到突破點，我們需要先深入思考新定義中的自相似點與三角形形狀之間的關系.首先思考的是：自相似點P如果存在，那么△ABC的內角需要滿足什么樣的條件？我們可以從特殊三角形進行探究，得出如下結論：

第一，在△ABC的邊上存在自相似點，當且僅當它的內角不全相等；

第二，在△ABC的內部存在自相似點，當且僅當它的內角都不相等.

進一步，我們可把三角形按邊進行分類，研究自相似點的相關情況，如表1所示：

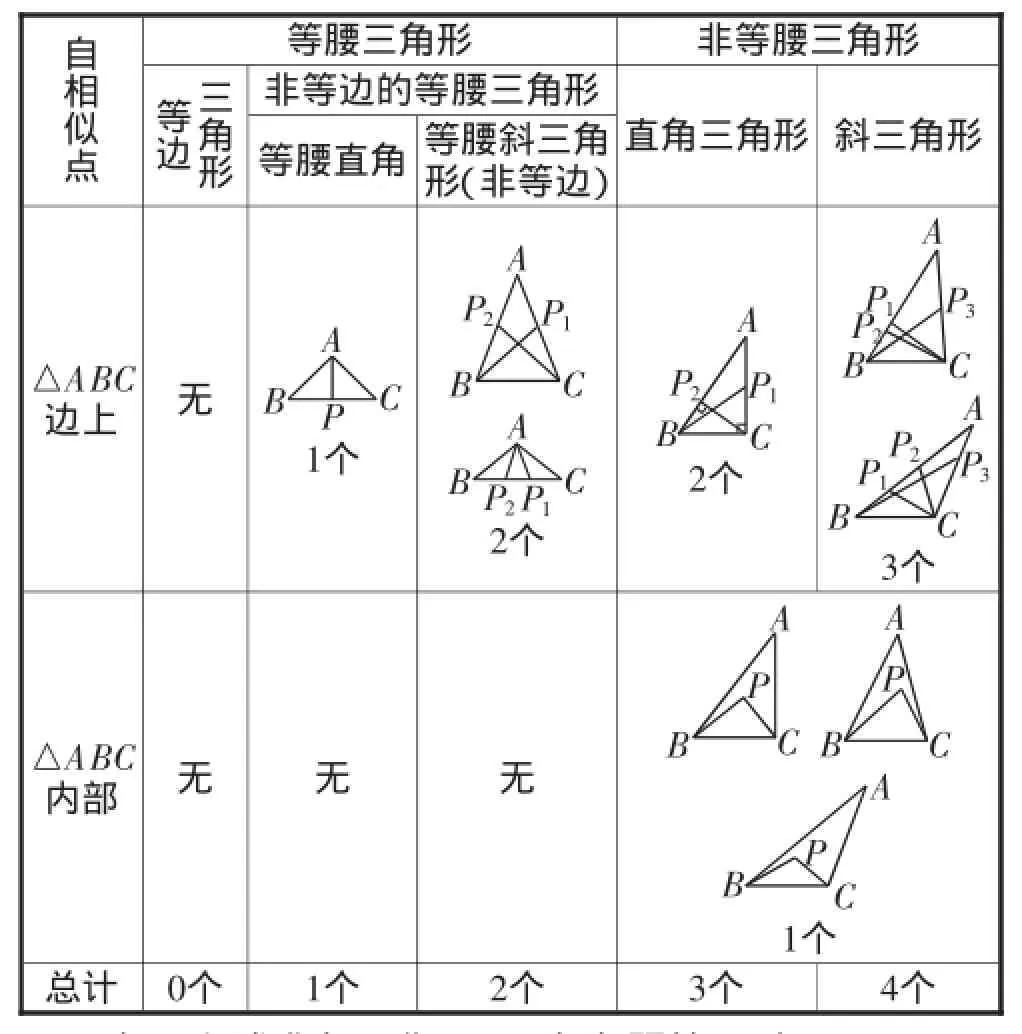
表1

有了上述準備工作，再思考考題第（2）問：

首先確定△OMN是等腰三角形（頂角為120°），則它的自相似點P一定在邊上，可分析出如圖4所示的草圖貫通思路.

接下來給出詳細思路：

①如圖5，過點M作MH⊥x軸于H點.

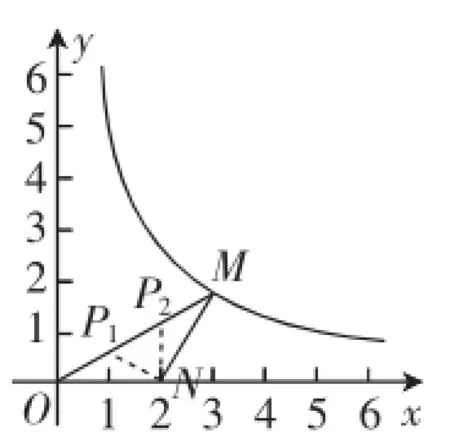
圖4

圖5

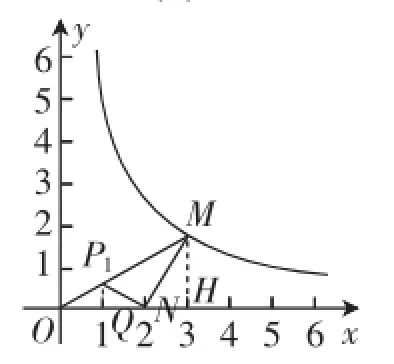
圖6

圖7

如圖6，△P1ON∽△NOM，過點P1作P1Q⊥x軸于Q點.

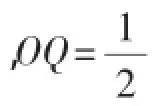
②首先想清△MON有兩個自相似點，則它是等腰（非直角）三角形.這樣問題的本質就是在曲線上確定點M，使△OMN是等腰三角形，可作出圖8輔助分析，即分別以O、N為圓心，NO為半徑作圓，與曲線有4個交點.注意：線段ON的垂直平分線與曲線的交點M5需要舍去，此時點M5（1，1）與O、N組成的△MON是等腰直角三角形，只有1個自相似點，這種情況應該舍去.

圖8

反思回顧：這道考題最后兩問比較抽象、晦澀，如果缺少對不同形狀三角形的自相似點的深入分析，并總結出如上文中的表格特點，則探究曲線上自相似點就會無從下手，尋找解題切入點遇到障礙.特別是最后一問中ON的中垂線與曲線的交點需要舍棄，也需要想清楚.

二、“新定義考題”的進一步賞析

新定義考題在各地中考試題中出現已有不少年份，但是像北京市這樣年年創新、年年不同，而且富有數學味、呈現簡約、引發深思的新定義考題卻不多見.不少低劣的新定義考題常常是把高中階段一些概念或性質簡單下放考查，使得考試的教學導向出現偏差，還有些地區的新定義考題出現理解晦澀甚至模糊不清的現象，不符合優秀試題追求簡潔好懂、富于生長的特點.具體來說，北京海淀區這道新定義考題還可提出如下賞析.

1.新定義清楚好懂，舉例說明助理解.

閱讀新定義，需要理解自相似點只能出現在△ABC內部或邊上，接著要辨別“何為自相似”，也就是解決新定義問題，要從解讀定義開始.為了幫助學生理解新定義，命題組舉例說明，并畫出圖形進行解讀，這樣有助于理解.這種命題思路在北京市近幾年中考壓軸題中都有體現，值得學習.

2.起步問題需構圖，特殊圖形助辨別.

考題的起步問題就將自相似點的確認放置在平面直角坐標系中進行研究，學生需要自主構造圖形，并確認三角形ABO的特殊形狀即真是一個含30°角的特殊直角三角形，并給出三個特殊點，標注出這些點之后，再發現這些點與其他邊構成的直角三角形中是否會出現含30°角的直角三角形，從而確定只有兩個點符合要求.這里從特殊出發解決問題的思路不僅對于這一道小題進行了處理，更重要的是要有“從特殊出發”“回到簡單”的解題心理，因為后續問題還是需要更為全面地分析不同三角形自相似點的個數.

3.挑戰考題有玄機，以退為進助突破.

考題的最后兩問與前面新定義之間跳開較大的距離，要想順利獲得解題念頭，則需要退回新定義，深入思考、全面分析不同形狀相似三角形自相似點的個數，也就是上文中那張表格的分析，這需要消耗學生較多的時間，且短時間內還不一定能想準思考方向.所以面對這樣的考題，在講評時建議安排學生先探究直角三角形自相似點的個數，再過渡到等腰三角形、等邊三角形自相似點的個數，待想清等腰三角形（非等邊）自相似點個數之后，再挑戰最后兩問，則可以很快獲得思路.這里需要讓學生積累以退為進的解題策略.

1.吳忠妙.一道考題的思路、難點與教學設計［J］.中學數學（下），2016（9）.

2.鄭毓信.多元表征與概念教學［J］.小學數學教育，2011（10）.

3.章建躍.構建邏輯連貫的學習過程使學生學會思考［J］.數學通報，2013（6）.