用于不平衡數據分類的0階TSK型模糊系統

顧曉清 蔣亦樟 王士同

模糊系統是對處理生產和實踐過程中的思維、分析、推理與決策等過程構建的一種數學模型,能夠將自然語言直接轉譯成計算機語言.由于具備不確定和模糊信息的處理能力,并具有高度的可解釋性和強大的學習能力,模糊系統在分類問題上受到廣泛關注,應用領域有信號處理,醫療診斷等[1?7]方面.模糊系統的參數學習一般可由專家經驗人為賦值或基于相關數據的學習來獲得,但很多情況下專家經驗并不存在或不完備,而后一種方法因其強大的學習能力在實踐中更具可行性.在現實生活中,不平衡數據的分類問題應用廣泛,例如,醫療診斷應用中,絕大部分對象都是正常人群,只有很少一部分是疾病患者;入侵檢測和釣魚網站識別應用中,異常樣本通常只占所有樣本非常小的比例.然而,在許多實際應用中,與多數類樣本相比,少數類樣本的有效識別更具有意義,也往往是研究者關注的重點對象.

確定所需規則數和規則空間的劃分以及確定模糊規則的后件參數是模糊系統建模的兩大關鍵技術[8].對于第一項,傳統模糊系統構建分類器時常采用聚類的方法,一種是不考慮樣本的標簽信息,在整個數據集上進行聚類;另一種是在每一個類別的樣本中獨立進行聚類,然后再將各聚類結果進行整合.但是,這兩種方法在處理不平衡數據分類問題時存在以下不足:前者由于沒有利用樣本的類別標簽信息,往往會因為少數類樣本的數量稀少而把少數類樣本視為異常點或噪聲;后者僅是簡單地將各類別樣本割裂開來,兩類樣本重疊區域會出現聚類中心間距過小或中心點重疊的現象.對于模糊規則的后件參數學習,傳統模糊系統一般遵循模型誤差最小化的原則,如文獻[9]中的遞推最小二乘法,文獻[10]中的不對稱最小二乘法,這類方法在處理樣本容量平衡的分類問題時具有較高精度.但是在處理不平衡數據的分類問題時,這類模糊系統往往傾向于追求多數類樣本的高識別率來達到整體樣本分類誤差的最小化,在這種情況下,分類面不可避免地會向少數類樣本發生偏移,少數類樣本的識別就存在較高的誤判率[11].因此,研究模糊系統在不平衡數據分類上的應用是有必要的和值得關注的.

目前針對不平衡數據的分類問題,在模糊系統領域一般通過過采樣或欠采樣技術來調整正負類樣本的比例,如文獻[12?13]采用過采樣技術給模糊規則設置不同權重來提高少數類樣本的分類精度;文獻[14?15]先定位樣本點的分布然后抽取不同類別的代表點實現類別間數據的平衡.文獻[16]提出了過采樣和欠采樣的結合方法來處理不平衡數據的分類問題.但是這類算法的缺點是會改變樣本的原始分布結構,采取精確復制少數類樣本的策略容易造成分類器的過擬合,而采取欠抽樣多類樣本的策略容易丟失部分樣本信息.另外,由于代價敏感學習[17?18]關注錯分樣本的代價,其相關算法也常用來解決不平衡數據的學習問題.

針對上述模糊系統在不平衡數據分類中前/后件參數學習的不足,本文提出了一種適用于不平衡數據分類的0階TSK型模糊系統(Zero-Order-Takagi-Sugeno-Kang fuzzy system for imbalanced data classi fi cation,0-TSK-IDC),能在較好地處理不平衡數據分類的同時,保證所得規則的可解釋性.鑒于0階TSK型模糊系統具有簡單性和可解釋性等優點[19],本文將其作為研究對象.0-TSK-IDC在不改變原有樣本分布結構的基礎上,從模糊規則的前件參數學習和后件參數學習兩個方面進行研究,首先,在模糊規則前件參數的學習上,受文獻[20]使用懲罰對手的競爭學習來加速聚類收斂性和文獻[21]防止聚類中心重合而最大化聚類中心間距的啟發,本文認為在樣本的類別標簽已知的情況下,不同類別樣本的聚類中心在學習過程中會產生了一種“競爭”關系,即聚類中心受同類別樣本的吸引向該類別的數據密集區域“靠近”,同時也受到其他類別樣本的“排斥”而被推離異類數據.本文將這一思想融入貝葉斯聚類(Bayesian fuzzy clustering,BFC)[22]模型中,提出了一種新的競爭貝葉斯模糊聚類(Bayesian fuzzy clustering based on competitive learning,BFCCL).BFCCL在聚類過程中考慮樣本的結構信息和不同類別聚類中心之間的排斥作用,采用不同類別樣本交替優化的策略,并通過馬爾科夫蒙特卡洛方法實現整個數據集的模糊劃分.BFCCL的優點在于能夠在類別不平衡的空間劃分中表現出準確性,有利于后件參數的學習,同時能有效增強所得模糊規則的可解釋性.

其次,本文設計的模糊規則后件參數學習的策略是在遵循分類面“大間隔”的同時考慮糾正分類面的偏移,使少數類樣本到分類面的距離大于多數類樣本到分類面的距離.該策略在目標函數的設計中同時考慮了結構風險和經驗風險,其訓練過程可轉化為二次規劃問題求解,保證結果的全局最優解,從而0-TSK-IDC模糊系統具有較高的泛化性和魯棒性.

本文結構如下:第1節回顧了相關工作,包括TSK型模糊系統和BFC算法的相關概念及原理;在此基礎上第2節提出了BFCCL算法;第3節提出了用于不平衡數據分類的0-TSK-IDC模糊系統;第4節通過在人工數據集和4個不平衡醫學診斷數據集上的實驗說明了BFCCL及0-TSK-IDC的有效性;第5節總結全文.

1 相關工作

1.1 TSK型模糊系統

經典模糊系統可分為3類[23?24]:Mamdani型模糊系統、Takagi-Sugeno-Kang(TSK)型模糊系統和Generalized模糊系統.其中,

TSK型模糊系統的第k個模糊規則的表示形式如下[25]:

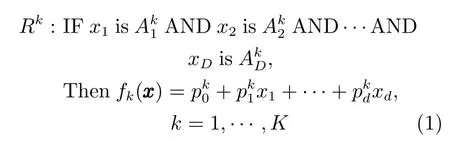
其中,TSK型模糊系統中每一條規則都有與之對應的輸入向量,并把輸入空間的模糊子集投影到輸出空間的模糊集為輸入向量xxx第i維所對應的第k條規則的模糊子集,K是模糊規則數,D是樣本維數.當模糊規則后件部分為一個實數值,即時,表示該模糊系統為0階TSK型模糊系統.由于0階TSK型模糊系統輸出的簡潔性,以及模糊規則后件參數更具有可解釋性,而受到廣泛關注.0階TSK型模糊系統的實值輸出為

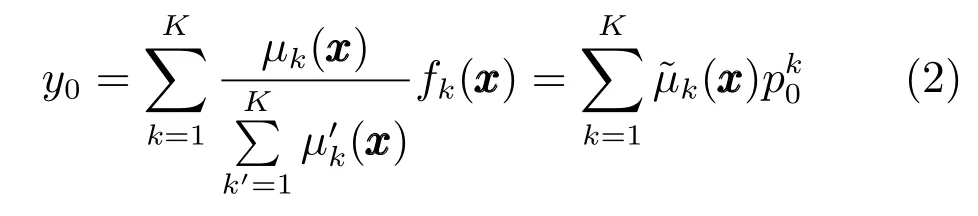
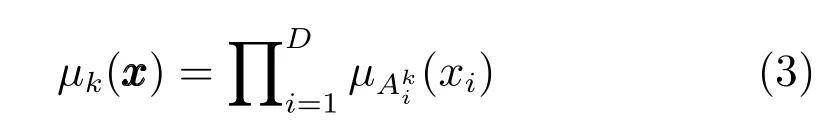
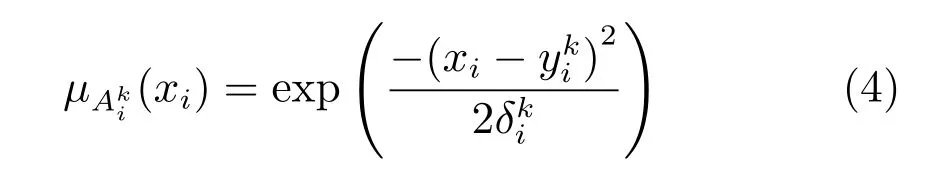
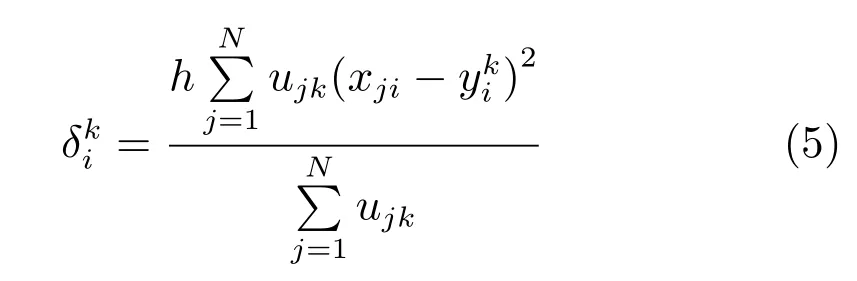
其中,ujk為輸入向量隸屬于第k類的模糊隸屬度,尺度參數h為一正常數.

傳統的0階TSK型模糊系統的規則后件參數學習常遵循模型誤差最小化原則[9?10],其可表示為

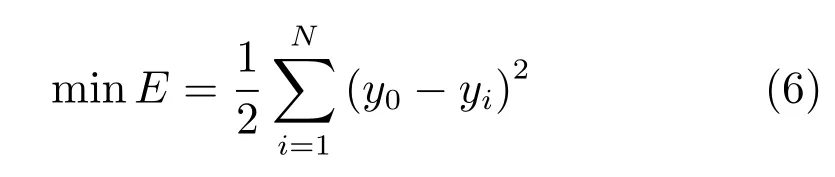
其中,yi為期望輸出.如在式(6)基礎上考慮結構風險最小化原則,規則后件參數的學習可轉化成線性回歸的二次規劃問題.但其在處理不平衡數據分類時,往往傾向于對多數類具有較高的識別率,而對少數類的識別率卻很低.

1.2 貝葉斯模糊聚類(BFC)

貝葉斯模糊聚類(BFC)算法[22]從概率的角度重新闡釋了FCM 聚類,并依據貝葉斯推理通過馬爾科夫蒙特卡洛(Markov chain Monte Carlo,MCMC)方法[27]來估計模型的最大后驗概率,得到隸屬度和聚類中心的全局最優解.對于給定的樣本集,BFC模型可表示為:

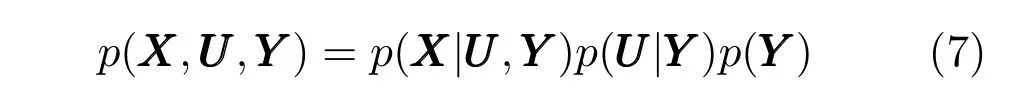
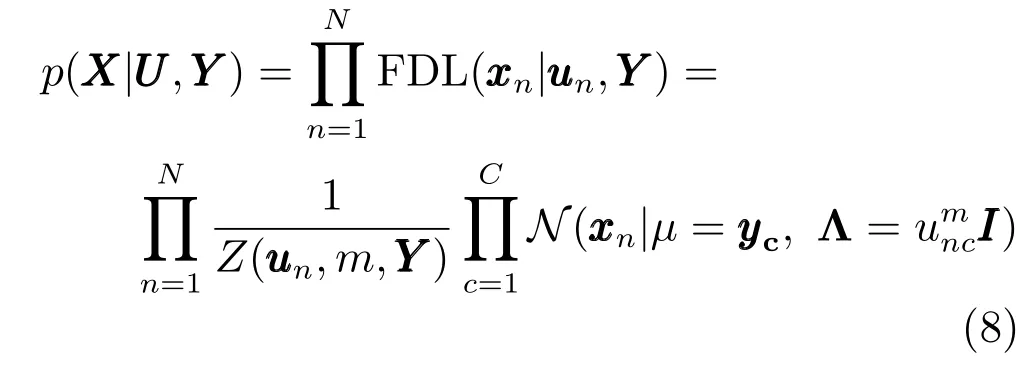
其中,N是樣本數,C是聚類數,unc是樣本屬于第c個聚類的隸屬度,m是模糊指數,是第c個聚類中心,是D維單位矩陣,是歸一化常數.BFC算法假設樣本服從正態分布為分布的中心,為分布的協方差矩陣.可見BFC中每個樣本具有獨立的概率分布.同一個聚類中的樣本分布共享一個期望值,但具有不同的協方差.

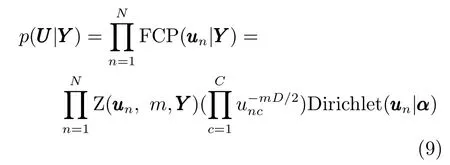
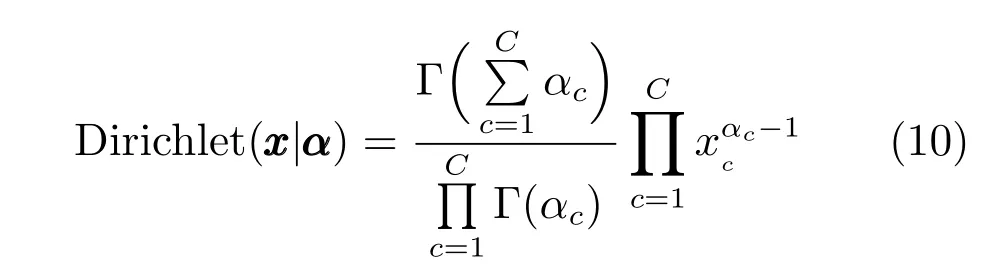
其中,xc≥0,c=1,···,C且.Dirichlet分布打破了FCM算法中模糊指數m必須大于1的限定,BFC算法中m值可以取任意實數.BFC模型假設每個聚類中心均滿足高斯分布,聚類中心先驗可以寫成:

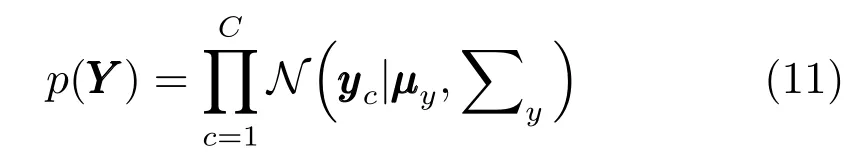
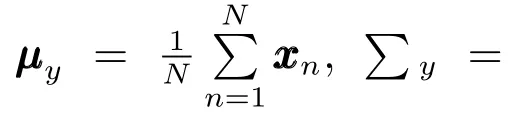
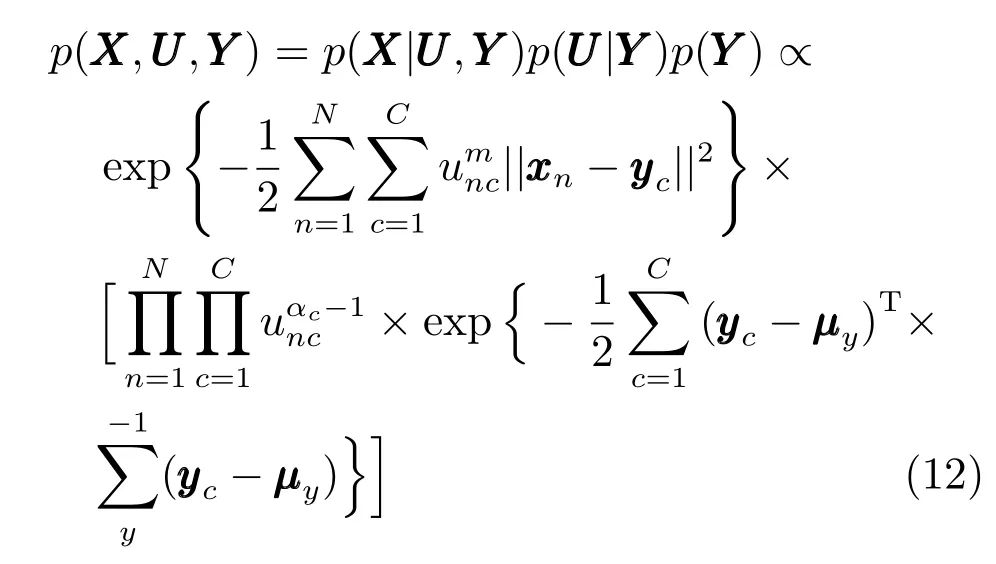
其中,符號“∝”表示兩邊僅相差一個不依賴于任何變量的常數因子.

2 競爭貝葉斯模糊聚類(BFCCL)

2.1 BFCCL基本思想

為了建立適用于不平衡數據分類的模糊規則前件參數學習方法,同時也為了提高所得模糊規則的準確性和可解釋性,本文提出了競爭貝葉斯模糊聚類(BFCCL).BFCCL聚類的出發點為:在聚類過程中,一類樣本會對另一類別的聚類中心產生排斥的影響,特別是在不同類別樣本的重疊區域,一方面,聚類中心受到本類別樣本的吸引而靠近該區域;另一方面,聚類中心受到異類別樣本的排斥而遠離該區域.這種排斥關系可表現為不同類別的聚類中心在樣本疊加區域的一種競爭學習關系.當樣本重疊區域的重疊密度越大時,屬于不同類別的聚類中心之間的競爭力也就越大.本文將這思想融入到BFC貝葉斯概率模型中,在樣本的類別標簽已知的前提下,采用在兩類樣本交替循環執行的策略,兩類的聚類中心分別作為已知數據,參與到另一類樣本聚類的過程中,起到聚類中心競爭學習的作用.兩類聚類中心交替影響,直至兩類聚類中心都處于穩定狀態.BFCCL聚類的構造原理示意圖如圖1所示.

2.2 目標函數的構造和參數學習方法

由圖1可知,BFCCL聚類通過兩類交替循環的策略實現數據集的最佳模糊劃分,本節以某一類樣本為例,重點闡述BFCCL聚類模型的目標函數和參數學習方法. 設給定某一類樣本集,聚類數為C1,假設另一類樣本的聚類中心已知,為,聚類數為C2.基于BFC模型的貝葉斯概率模型,樣本XXX服從正態分布,并且每個樣本具有獨立的概率分布,因此BFCCL聚類中樣本集XXX中數據和參數的聯合概率模型可表示為式(13).

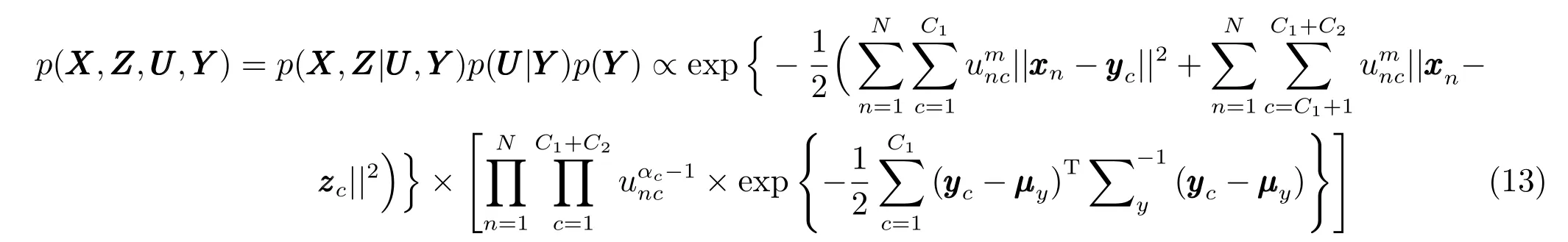
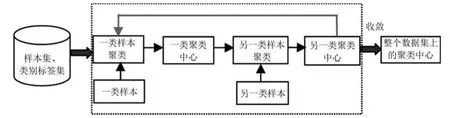
圖1 BFCCL聚類的構造原理示意圖Fig.1 The principle of BFCCL clustering

其中,樣本集和另一類聚類中心矩陣為模型的已知數據,需構建的聚類中心矩陣和模糊隸屬度矩陣是模型的參數.通過對上式取對數,可得BFCCL模型的目標函數:

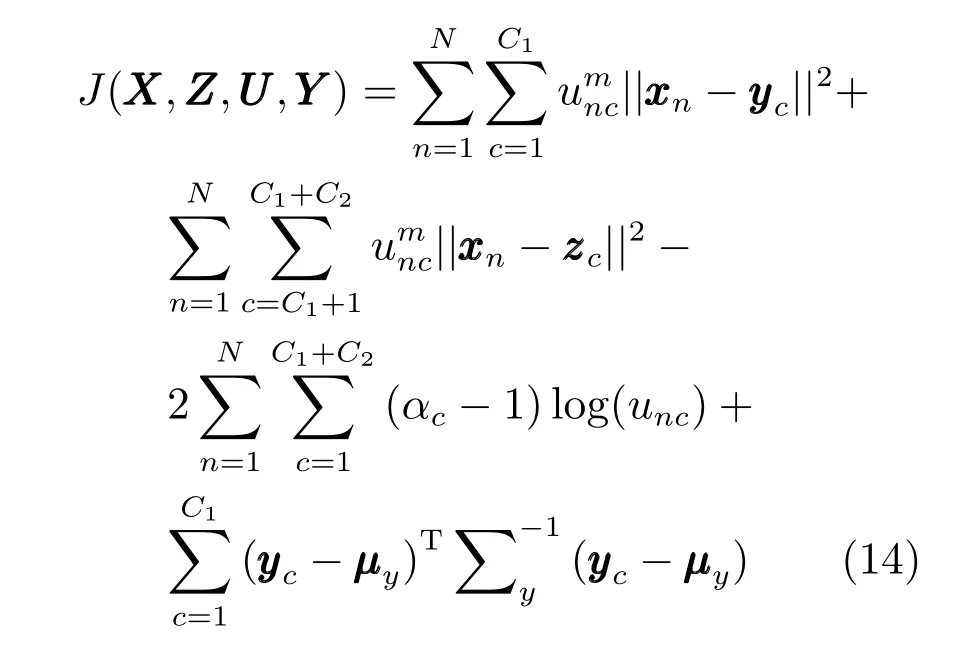
結合上述聯合概率模型(13)和目標函數式(14),給出如下分析和說明:

1)不同于常規聚類方法不考慮樣本所帶的標簽信息,BFCCL模型目標函數中的前2項表示出不同類別的聚類中心間的競爭關系.在另一類樣本的聚類中心已知的前提下,待求聚類中心必然會與這些已知聚類中心對模糊隸屬度產生“競爭”關系,這種競爭關系可理解為不同類別聚類中心間的相互排斥關系;同時這種競爭關系能保證空間劃分的清晰性和增強所得模糊規則的準確性和可解釋性.

2)由圖1可知,為了獲得整個數據集的最佳空間劃分,需在正負類樣本上采取交替循環的策略來求解式(13)的最大后驗值.在循環的過程中兩類聚類中心相互影響,直至兩類的聚類中心處于穩定狀態.

3)模糊指數m起到調節競爭力強弱的作用,m的值越大,聚類中心間的競爭力就越弱;反之,m的值越小,聚類中心間的競爭力就越強.

為了獲得最優模糊隸屬度矩陣和聚類中心矩陣,BFCCL通過先后兩次使用Metropolis-Hastings(MH)采樣[27]構造一條Markov鏈來獲得模型參數的最大后驗值,其參數的學習過程如圖2所示.從圖2可知,該Markov鏈的第n次迭代的過程可主要分為3步:

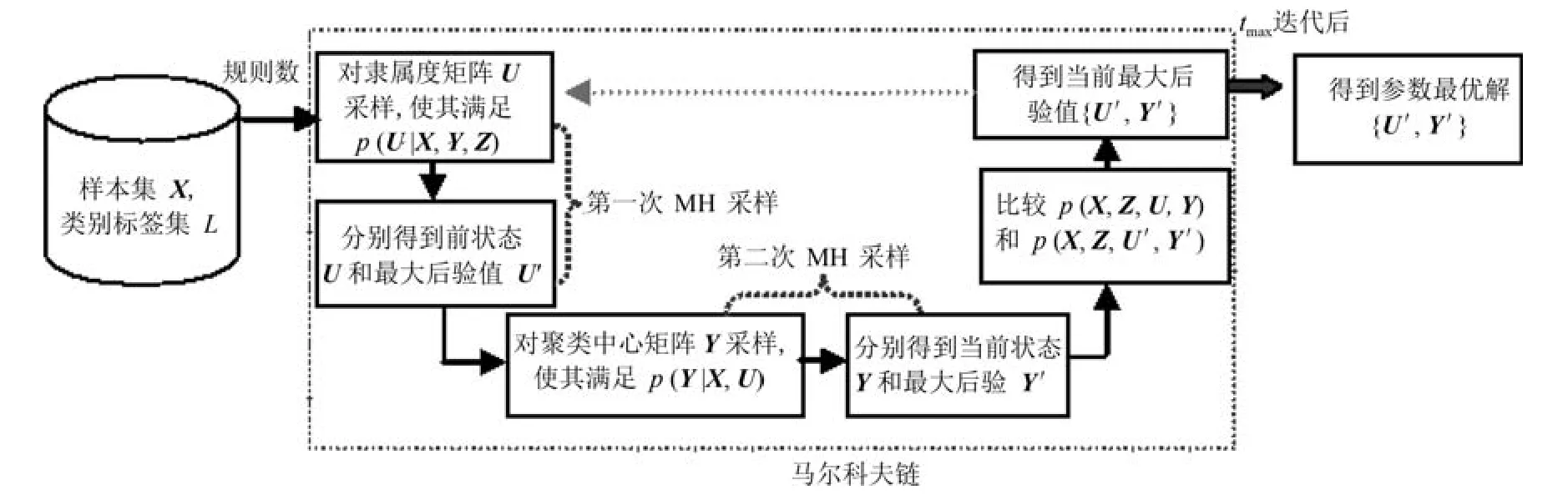
圖2 BFCCL參數學習示意圖Fig.2 The parameter learning strategy of BFCCL

步驟1.在給定樣本和聚類中心的情況下,使用Metropolis-Hastings方法對模糊隸屬度進行采樣:

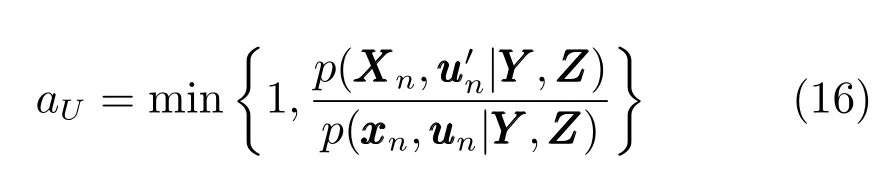
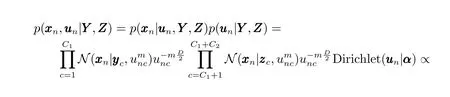
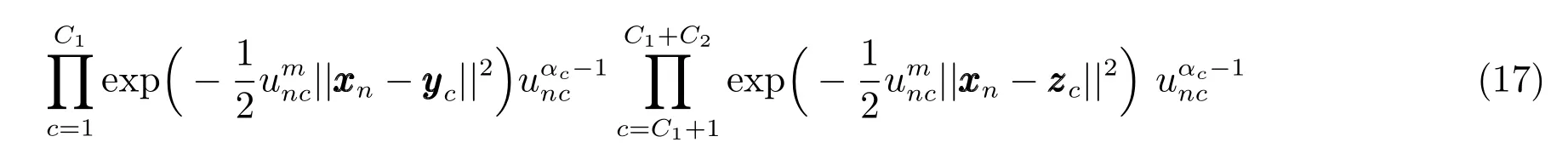
步驟2.為了獲得聚類中心矩陣的最優值,BFCCL使用Metropolis-Hastings方法對進行采樣:

a)通過以下正態分布對聚類中心進行采樣,即

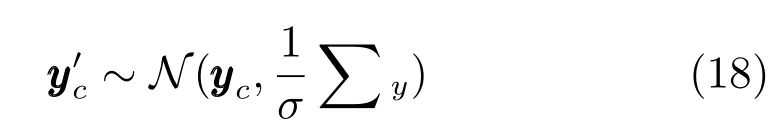
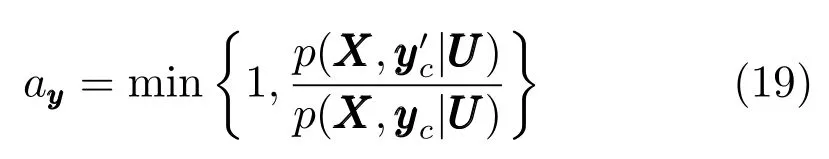
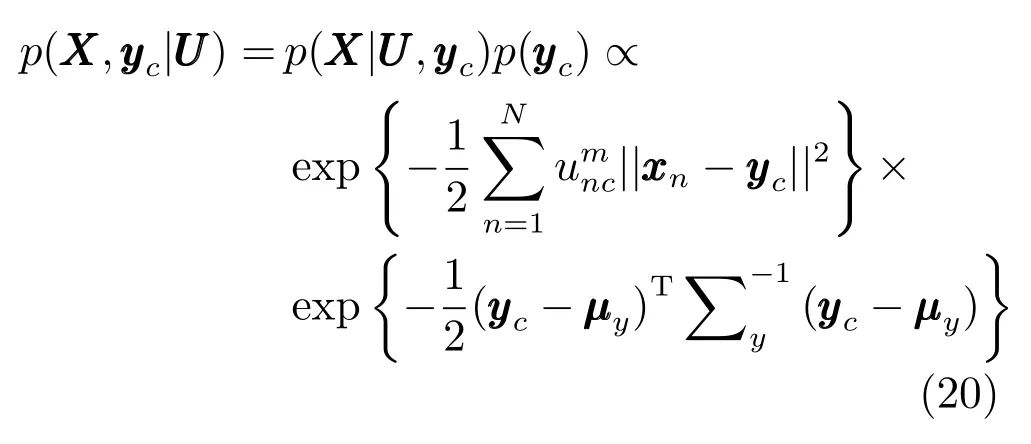
步驟3.根據式(13)計算的值并與當前的值進行比較,若,則用替換當前的.

2.3 BFCCL聚類算法

本文將研究重點置于最基本的二元分類問題.結合圖1所示的BFCCL聚類構造原理示意圖和第2.2節的內容,本節給出BFCCL聚類算法在整個數據集上實施的具體步驟,見算法1. 設全體樣本和其對應的類別標簽,其中和分別表示正負兩類樣本.為了獲得全體樣本的最佳空間劃分,需在正負類上采取交替循環的策略來執行式(13).兩類聚類中心交替影響,直至兩類的聚類中心處于穩定狀態.

BFCCL聚類采取兩類樣本交替循環執行的策略來獲得聚類中心和模糊隸屬度的最優解,BFCCL聚類中單次循環的時間復雜度主要在于步驟2的執行,而步驟2又由兩部分構成:計算模糊隸屬度矩陣和聚類中心矩陣,前者的時間復雜度由式(17)產生,為O(NCD+CD2);后者的時間復雜度由式(20)產生,為O(CD2).因此,BFCCL聚類算法執行的時間復雜度為O(vmaxtmax(NCD+CD2)),其中tmax和vmax分別是算法正負類交替迭代和Metropolis-Hastings采樣方法中迭代的次數.另外,實驗中一般可將式(18)中的協方差矩陣設為對角陣,此時,算法1的復雜度可減少至O(vmaxtmaxNCD).可見,BFCCL聚類算法運行的時間效率與樣本的分布和結構有關,為了在一定程度上提高本文方法的執行效率,可以采用KPCA等降維方法對樣本進行相應的預處理,或者采用正交三角(QR)等分解法對式(20)中的協方差矩陣進行變換處理.

算法1.BFCCL聚類算法

輸入.正負兩類數據集和,模糊指數m,正、負類樣本的聚類個數分別為C(1)和C(2),MH采樣最大迭代次數vmax,兩類交替循環最大迭代次數tmax,誤差閾值ε;

輸出.模糊隸屬度矩陣和聚類中心.

初始化.在數據集和分別計算正負類樣本的均值和協方差;在數據集和分別進行兩類模糊隸屬度矩陣和進行初始化,其中矩陣中的元素矩陣中的元素;在數據集和分別對兩類聚類中心矩陣和進行初始化,其中矩陣中的元素:矩陣中的元素;在數據集和分別對模糊隸屬度矩陣和聚類中心矩陣的最大后驗值進行初始化,;

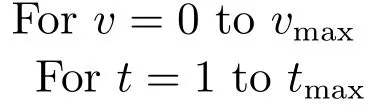
步驟1.令

步驟2.

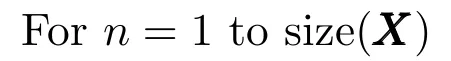
{步驟2.1.根據式(15)得到隸屬度;

步驟2.2.根據式(16)計算和,并以式(17)的概率接受;

步驟2.3.根據式(17),如果,那么;

步驟2.4.如果n＞N,則轉至步驟2.5;否則,置n=n+1,并返回步驟2.1};

Endn

Forc=1 to size(C1)

{步驟2.5.根據式(18)采樣新的聚類中心;

步驟2.6.以式(19)的概率接受;

步驟2.7.根據式(20),如果,那么;

步驟2.8.如果c＞C1,則轉至步驟2.9;否則,置c=c+1,返回步驟2.6;

步驟2.9.如果,那么

Endc

步驟2.10.如果t＞tmax,則將和分別設置為當前樣本的模糊隸屬度矩陣和聚類中心矩陣的最大后驗值并轉至步驟3;否則,轉至步驟2.1;

步驟3.令

步驟4.轉向步驟2

Endt

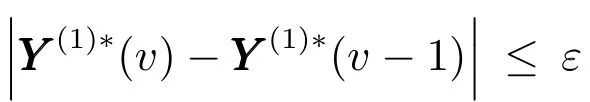
Endv.

3 用于不平衡數據分類的0階TSK型模糊系統(0-TSK-IDC)

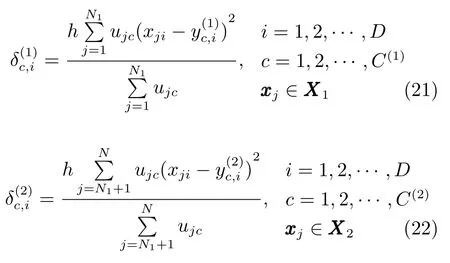
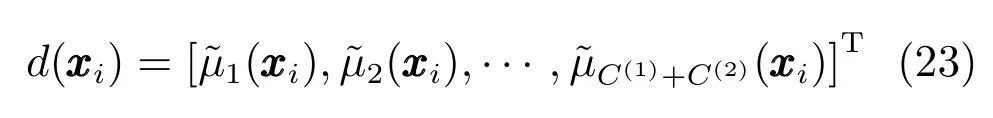
傳統分類面的大間隔的策略是達到兩類間距離的最大化,但這種分類面在處理不平衡分類問題中易向少數類發生偏移.為糾正分類面的偏移,本文尋找的分類面在達到兩類間距離的最大化的同時,保證少數類到分類面的距離不得小于多數類到分類面的距離,其示意圖如圖3所示.因此后件參數的學習問題可用以下最優化問題來表示:

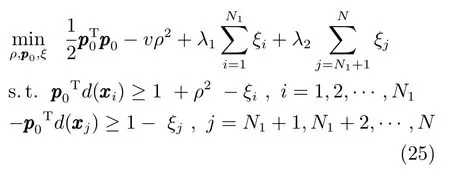
其中,v,λ1和λ2為 3個正常數,且λ1/λ2=N2/N1=(N?N1)/N1.

求解式(25)可以利用Lagrange技巧,引入非負的Lagrange因子方程的各變量求偏導數,并令各偏導方程為零,上述最優化問題可以轉換成對偶形式:

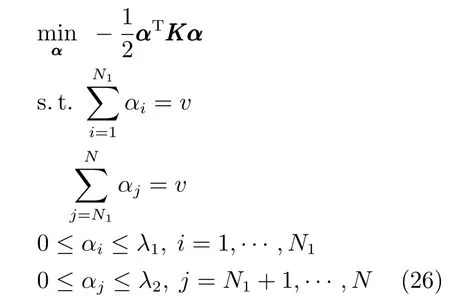
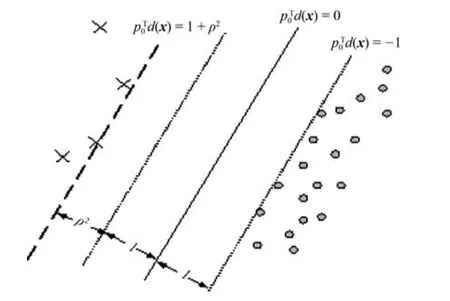
圖3 0-TSK-IDC分類面示意圖Fig.3 The classi fi cation hyperplane of 0-TSK-IDC

引理1[28].令是上的一個緊集,是Mercer核當且僅當是上連續對稱函數且關于任意的的Gram矩陣半正定.

定理1.如果模糊系統中前件的模糊隸屬函數是連續函數,則式(26)的核函數是Mercer核.

證明.根據式 (26)的定義,,容易看出是一個實對稱矩陣.其次,對任意的,由式(23),有且是連續函數,因此核函數是Mercer核.

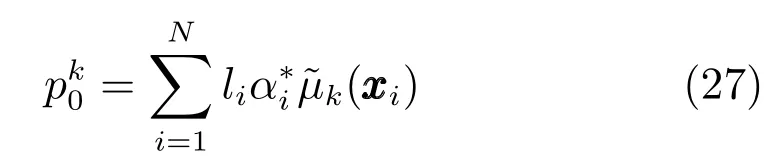
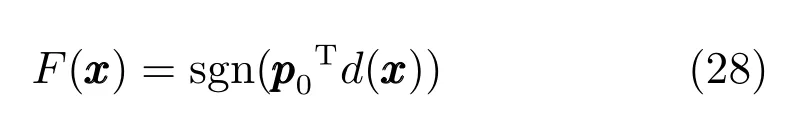
根據上文的分析和推導,0-TSK-IDC使用BFCCL算法得到準確性和可解釋性強的規則前件參數,規則后件參數著眼于分類面的偏移糾正.這里總結出0-TSK-IDC模糊系統的具體訓練步驟,具體如下:

算法2.0-TSK-IDC模糊系統

輸入.數據集,模糊規則數(C(1)+C(2)),模糊指數m,尺度參數h,MH采樣最大迭代次數vmax,兩類交替循環最大迭代次數tmax,誤差閾值ε,調節參數v,正則化參數λ1和λ2;

輸出.分類決策函數F(xxx).

步驟 1.根據算法1得到隸屬度矩陣,和聚類中心矩陣;

步驟2.由式(22)計算高斯隸屬度函數的方差矩陣δ(1)和δ(2);

步驟 3.由式(3)～(5)0-TSK-IDC將原始數據集映射至特征空間形成新的數據集;

步驟 4.由式(26)求解得到Lagrange因子α;

步驟5.由式(27)得到0-TSK-IDC的后件參數;

步驟6.由式(28)得到0-TSK-IDC的決策函數.

0-TSK-IDC模糊系統的時間復雜度主要集中在算法1和二次規劃求極值問題上.二次規劃問題的時間復雜度為O(N3),因此,0-TSK-IDC模糊系統的時間復雜度為O(vmaxtmax(NCD+CD2)+N3).本文使用SMO(Sequential minimal optimization)[20]等分解方法處理二次規劃問題,0-TSK-IDC模糊系統的時間復雜度降低至O(vmaxtmax(NCD+CD2)+N2).

需要指出的是,0-TSK-IDC模糊系統后件參數的學習策略與支持向量機(Support vector machine,SVM)[29]較為相似,但這兩種方法之間存在著本質差異,0-TSK-IDC通過模糊規則完成特征空間的映射,而SVM 通過核函數直接將原始數據映射到特征空間上;其次,0-TSK-IDC分類決策函數中的參數同時也是模糊系統中模糊規則的參數,其具有高度的語義性和可解釋性,這一特性是模糊系統特有的.

4 實驗結果與分析

4.1 實驗設置

一般認為當少數類與多數類的樣本比例低于1:2時,數據集具有不平衡特征．而現實生活中的醫學診斷數據往往呈現出不平衡性,本文的實驗部分將利用人工Banana數據集[30]和4個UCI醫學數據集[31](基本信息見表1)所示對BFCCL算法和0-TSK-IDC模糊系統進行驗證和評價.依照不平衡數據分類問題中常用的設定方法,實驗中將少數類指定為正類,將多數類指定為負類.

表1 數據集的基本信息Table 1 The basic information of datasets

本文的實驗分成兩個部分:1)0-TSK-IDC中規則前件參數學習分別使用BFCCL算法和BFC算法來進行性能的比較;2)0-TSK-IDC模糊系統與 FS-FCSVM[32]、L2-TSK-FS[25]、Adaboost[33]和 CS-SVM[34]算法進行性能的比較,其中 FSFCSVM和L2-TSK-FS是基于模糊聚類的模糊系統;Adaboost和CS-SVM 是處理不平衡數據分類的算法.為了驗證本文所提的模糊規則的后件參數學習方法在不平衡分類問題上的有效性,實驗中還將0-TSK-IDC模糊系統與BFCCL-TSK-FS模糊系統進行了對比,BFCCL-TSK-FS模糊系統中規則前件參數的學習使用BFCCL聚類方法;規則后件參數的學習使用與FS-FCSVM模糊系統相同的方法,即標準的SVM算法.

實驗參數設置如下:0-TSK-IDC中最大迭代次數tmax=103,vmax=103,式(19)中的參數σ=3,誤差閾值ε=10?5,根據文獻[35]模糊指數m取值為2,此時物理意義最明確,其他可人工設定的參數通過網格搜索的方式來確定,尺度參數h取值為{0.22,0.42,···,22},調節參數v取值為{1,5,···,30},正則化參數λ2取值為{10?3,···,103},λ1的值根據λ1=λ2N2/N1來確定,模糊規則數C1和C(2)取值均為{1,2,···,10}.實驗中,FS-FCSVM 和L2-TSK-FS的規則前件由FCM聚類獲得,模糊指數m取值為2,規則后件學習的正則化參數的設置與λ2相同.CSSVM 算法中的核函數采用高斯核,核參數取值為{10?3,···,103}, 正則化參數的設置與λ1和λ2相同.Adaboost算法中設置弱分類器的個數為10.BFCCL-TSK-FS算法中BFCCL聚類的參數設置參照0-TSK-IDC,其他參數的設置參照FS-FCSVM.

為了更好地呈現出不同程度的非平衡性對算法性能產生的影響,本文采用G-mean和F-measure[36?37]兩種評價準則來評價算法的分類性能:

其中,G-mean是關注數據集整體分類性能的評價指標,Positive Accuracy=Recall=TP/(TP+FN),Negative Accuracy=TN/(TN+FP)為真負率.F-measure是查全率和查準率的調和均值,Recall=TP/(TP+FN)為查全率,Precision=TP/(TP+FP)為查準率,β通常設置為1.這2個評價準則中用到的TP指標是指被正確分類的正類樣本的數目,FN指標是指被錯誤分類的正類樣本的數目,FP指標是指被錯誤分類的負類樣本的數目,TN指標是指被正確分類的負類樣本的數目.可見,G-mean準則可以合理地評價在保持正、負類分類精度平衡下最大化兩類的精度,而F-measure準則可以合理地評價分類器對于少數類的分類性能．本文實驗中每個數據集進行5折交叉驗證,運行5次以平均后的G-mean和F-measure作為最終分類精度.本文的實驗在2.53GHz quadcore CPU,8GB RAM,Windows 7系統下執行,所有算法均在Matlab 2009b環境下實現.

4.2 BFCCL與BFC在0-TSK-IDC模糊分類器中的性能比較

4.2.1 人工數據集

實驗中構造了3組正負類比例不同的Banana數據集,即:選取全部1500個負類樣本,并分別隨機選取600,200,100個正類樣本.圖4～7是分別使用BFC和BFCCL算法正負類聚類數均為3和4時,交叉驗證中某一折的聚類結果示意圖,兩圖中正類樣本分別是480,160和80個(用黑點表示),負類樣本均為1200個(用灰點表示),正類和負類的聚類中心分別用黑色和白色矩形表示.可以看出:

1)當在正負兩類樣本中分別使用BFC算法聚類時,圖4中(a)～(c)中負類樣本的聚類效果完全相同,圖6亦如此.同時在樣本重疊區域出現了聚類中心間的距離狹小的現象,自然由此聚類效果得到的模糊規則的模糊集會存在交叉和重疊的現象.這是因為BFC聚類不考慮不同類別聚類中心間的排斥關系,運用到模糊系統前件學習中時,得到的模糊規則其清晰性得不到保證.

圖4 BFC在Banana集上正負類聚類數均為3時的聚類效果Fig.4 The clustering results on the Banana dataset in BFC with three clustering on the positive and negative classes,respectively

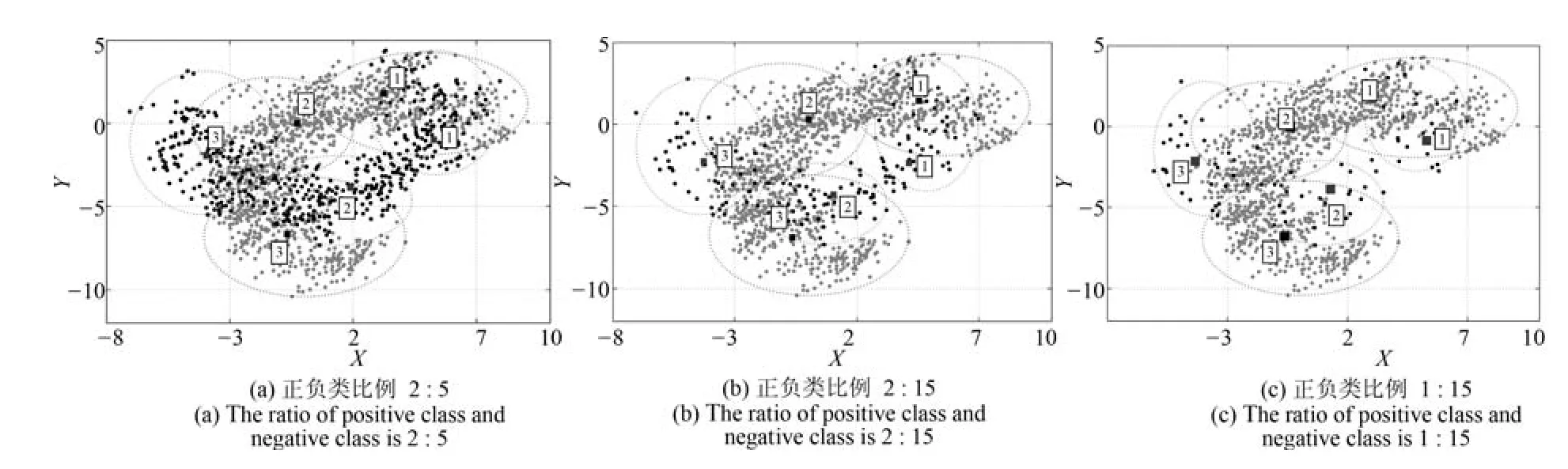
圖5 BFCCL在Banana集上正負類聚類數均為3時的聚類效果Fig.5 The clustering results on the Banana dataset in BFCCL with three clustering on the positive and negative classes,respectively

圖6 BFC在Banana集上正負類聚類數均為4時的聚類效果Fig.6 The clustering results on the Banana dataset in BFC with four clustering on the positive and negative classes,respectively

2)BFCCL算法考慮了在樣本重疊區不同類別聚類中心的競爭關系,聚類中心由于受到另一個類別樣本的排斥而盡量地遠離該區域,這種排斥力最終促使正負類樣本的聚類中心盡可能地遠離對方樣本區域,從圖5和圖7的聚類效果可知,隨著正類樣本數量和分布的變化,其對負類樣本的聚類中心的排斥力的強弱也發生了變化,負類樣本的聚類效果也隨之受到了影響.因此在樣本重疊區域不會發生聚類中心間的距離狹小的情況.

圖8給出了0-TSK-IDC模糊系統基于圖7(b)聚類結果所獲得的模糊集示意圖.我們知道,聚類中心(即模糊規則中心)的分布是決定所獲得的模糊規則清晰性和可解釋性的決定性因素之一.由圖8可知,BFCCL聚類中的不同類別間聚類中心競爭學習的策略可以保證獲得的模糊規則具有良好的可解釋性.表3為0-TSK-IDC模糊系統中規則前件分別使用BFCCL與BFC算法的性能比較.根據表3結果可知,在正負類樣本具有不同比例不平衡性的情況下,與BFC聚類相比,使用BFCCL聚類獲得的解釋性強的規則前件參數有助于提高0-TSK-IDC模糊系統的分類性能,此時G-mean和F-measure指標均有相應的提高.

4.2.2 真實數據集

為了對BFCCL聚類算法性能作進一步地探討和分析,本節使用4個不平衡UCI醫學診斷集對BFCCL與BFC算法應用到模糊規則前件參數學習時,所得的0-TSK-IDC模糊系統的分類性能進行比較.G-mean和F-measure值及其方差的比較結果如表3所示.從表3結果可知,真實數據集上的實驗結果與上一節人工數據集實驗上觀察到的結果基本保持一致,在0-TSK-IDC模糊系統中使用BFCCL算法方法后F-measure和G-mean評價指標均高于使用BFC算法的情況,說明在使用聚類算法獲取模糊規則前件參數的學習中,充分考慮不同類別聚類中心之間的競爭關系,有助于提升模糊空間劃分的準確性和清晰性.

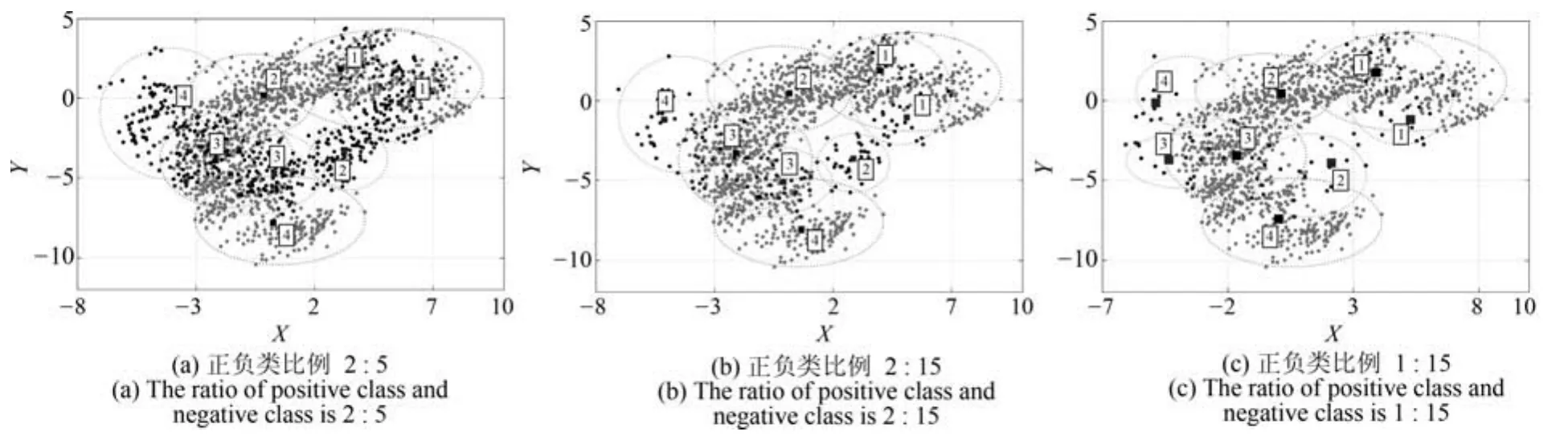
圖7 BFCCL在Banana集上正負類聚類數均為4時的聚類效果Fig.7 The clustering results on the Banana dataset in BFCCL with four clustering on the positive and negative classes,respectively

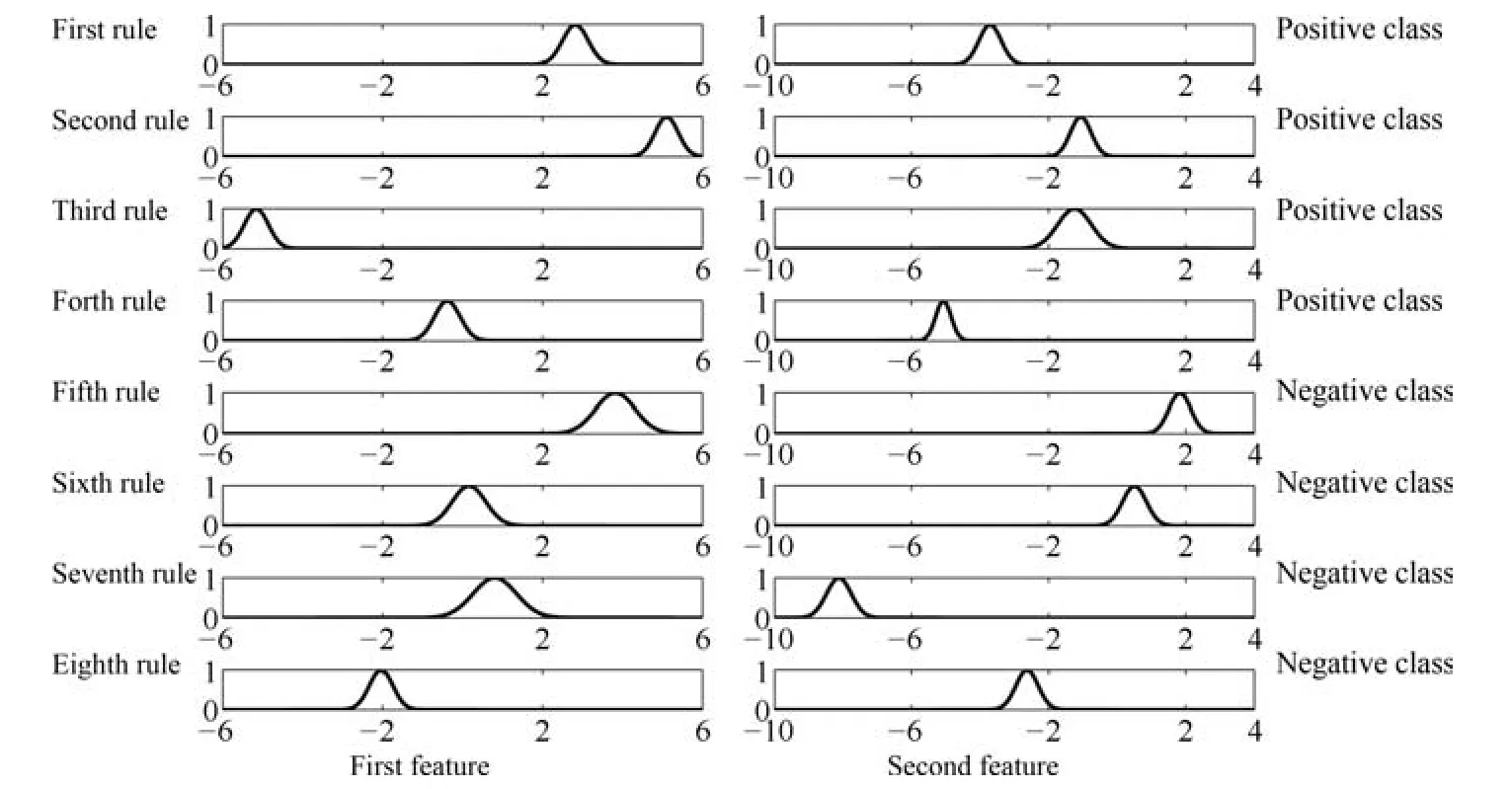
圖8 0-TSK-IDC基于圖7(b)聚類結果的所獲得模糊集示意圖Fig.8 A plot of rulebase of 0-TSK-IDC from the clustering result in Fig.7(b)

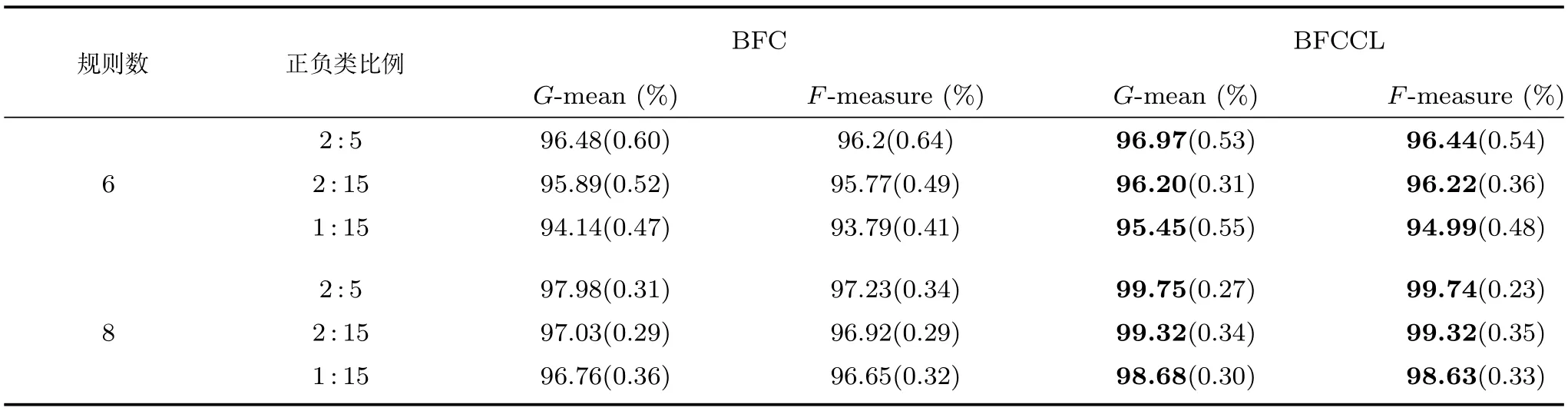
表2 Banana集上基于BFC與BFCCL圖4～7聚類結果的0-TSK-IDC模糊系統中的G-mean和F-measure及其方差的比較Table 2 G-mean,F-measure and their standard deviations comparison of 0-TSK-IDC with the clustering results in Fig.4～7 by using the BFC and BFCCL on the Banana dataset

表3 UCI醫學集上分別使用BFCCL與BFC得到規則前件時0-TSK-IDC模糊系統中的G-mean和F-measure值及其方差的比較Table 3 G-mean,F-measure and their standard deviations comparison of 0-TSK-IDC with BFC and BFCCL on UCI datasets

4.3 0-TSK-IDC模糊分類器與相關分類算法性能比較

為了對0-TSK-IDC模糊分類器的性能進行評估,本節對0-TSK-IDC與FS-FCSVM、L2-TSKFS、BFCCL-TSK-FS、Adaboost和CS-SVM 五種分類算法進行比較.

4.3.1 人工數據集

本節依舊采用與第4.2.1節相同的Banana數據集進行訓練和測試,表4列出了6種對比算法的G-mean和F-measure指標的比較.從實驗結果可以看出,隨著Banana數據集中正負類不平衡比例的提高,6種算法的F-measure和G-mean指標都呈現出一定的下降趨勢,可見,數據的不平衡性將嚴重影響分類的效果.特別是FS-FCSVM、L2-TSK-FS和BFCCL-TSK-FS算法,由于未考慮類別不平衡性,當正類樣本太少而不能充分學習會導致分類面向正類樣本發生了較大的偏移,其結果是正類樣本的分類準確率迅速降低,因而G-mean和F-measure指標值也迅速降低.由于充分考慮了不同類別的聚類中心間的競爭學習及數據的不平衡性,本文提出的0-TSK-IDC模糊系統在分類性能上相比其他5種算法都有提高.CS-SVM算法更多地考慮少數類即正類樣本的分類代價,對正類樣本的識別率較高而負類樣本的識別率較低;而Adaboost算法通過過采樣技術來增加少數類樣本的數量,由于改變了樣本的分布結構容易造成分類器過擬合的情況.因此,這兩種算法獲得的G-mean和F-measure指標值在絕大多數情況下均落后于0-TSK-IDC.

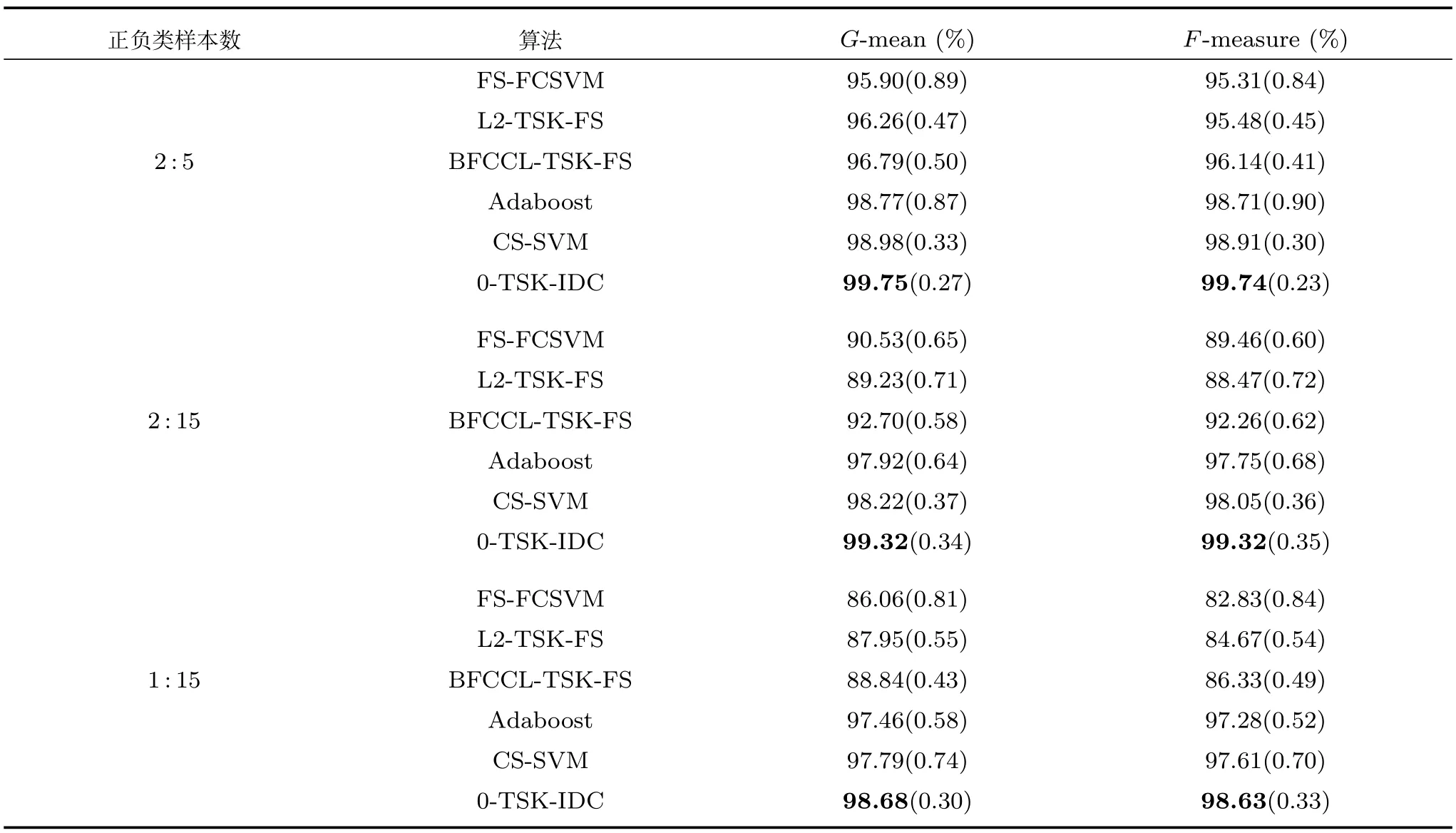
表4 Banana數據集上0-TSK-IDC模糊分類器與其他算法的G-mean和F-measure值及其方差的比較Table 4 G-mean,F-measure and their standard deviations comparison of 0-TSK-IDC and other algorithms on the Banana dataset

4.3.2 真實數據集

本節給出0-TSK-IDC、FS-FCSVM、BFCCLTSK-FS、L2-TSK-FS、Adaboost和 CS-SVM 算法在4個UCI醫學診斷數據集上的性能比較,G-mean和F-measure變化曲線如圖9和圖10所示.從實驗結果可以看出,

1)UCI數據集上獲得的實驗結果與人工數據集的實驗結果是一致的.本文所提的0-TSK-IDC在不同程度的類別不平衡場合均表現出優良的分類性能;特別對不平衡性較大的數據集,0-TSK-IDC更能體現其較強的魯棒性.其原因在于0-TSK-IDC模糊系統前件參數的學習使用了BFCCL聚類,BFCCL聚類通過類別間競爭學習的策略能合理獲取不平衡兩類上的空間劃分,能保證獲得的模糊規則中的模糊集的準確性和可解釋性;0-TSK-IDC模糊系統后件參數的學習從糾正分類面的偏移入手,最終得到的分類面在達到兩類間距離的最大化的同時,保證少數類到分類面的距離不小于多數類到分類面的距離.

2)真實數據集上類別間樣本數量的不平衡性嚴重影響算法的分類性能,如圖9和圖10所示,隨著實驗中類別不平衡性的加劇,三種模糊系統FS-FCSVM、L2-TSK-FS和BFCCL-TSK-FS得到的G-mean和F-measure值也急劇下降.但由于BFCCL-TSK-FS能夠借助BFCCL聚類算法得到準確的空間劃分結果,所以其分類效果要優于FS-FCSVM和L2-TSK-FS,具體表現為BFCCLTSK-FS在4個UCI數據集上獲得的G-mean和F-measure值均高于FS-FCSVM和L2-TSK-FS獲得的值.

3)Adaboost和CS-SVM算法在G-mean和F-measure值上得到的結果較為相近,與FSFCSVM、L2-TSK-FS和BFCCL-TSK-FS這三種模糊系統相比,兩者具有明顯的優勢;但與0-TSKIDC相比兩者的性能略差.值得注意的是,0-TSKIDC模糊系統另一個突出優點是其構建的模糊規則具有高度的可解釋性,而這一特性是Adaboost和CS-SVM算法所不具備的.

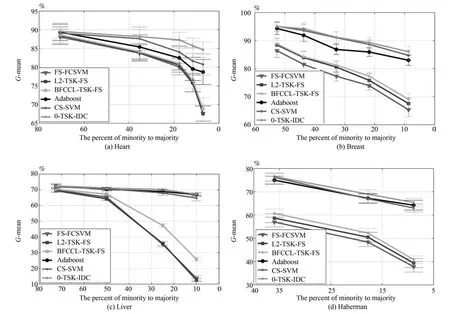
圖9 UCI醫學集上不同算法的G-mean比較Fig.9 G-mean and its standard deviation comparison of 0-TSK-IDC and other algorithms on UCI dataset

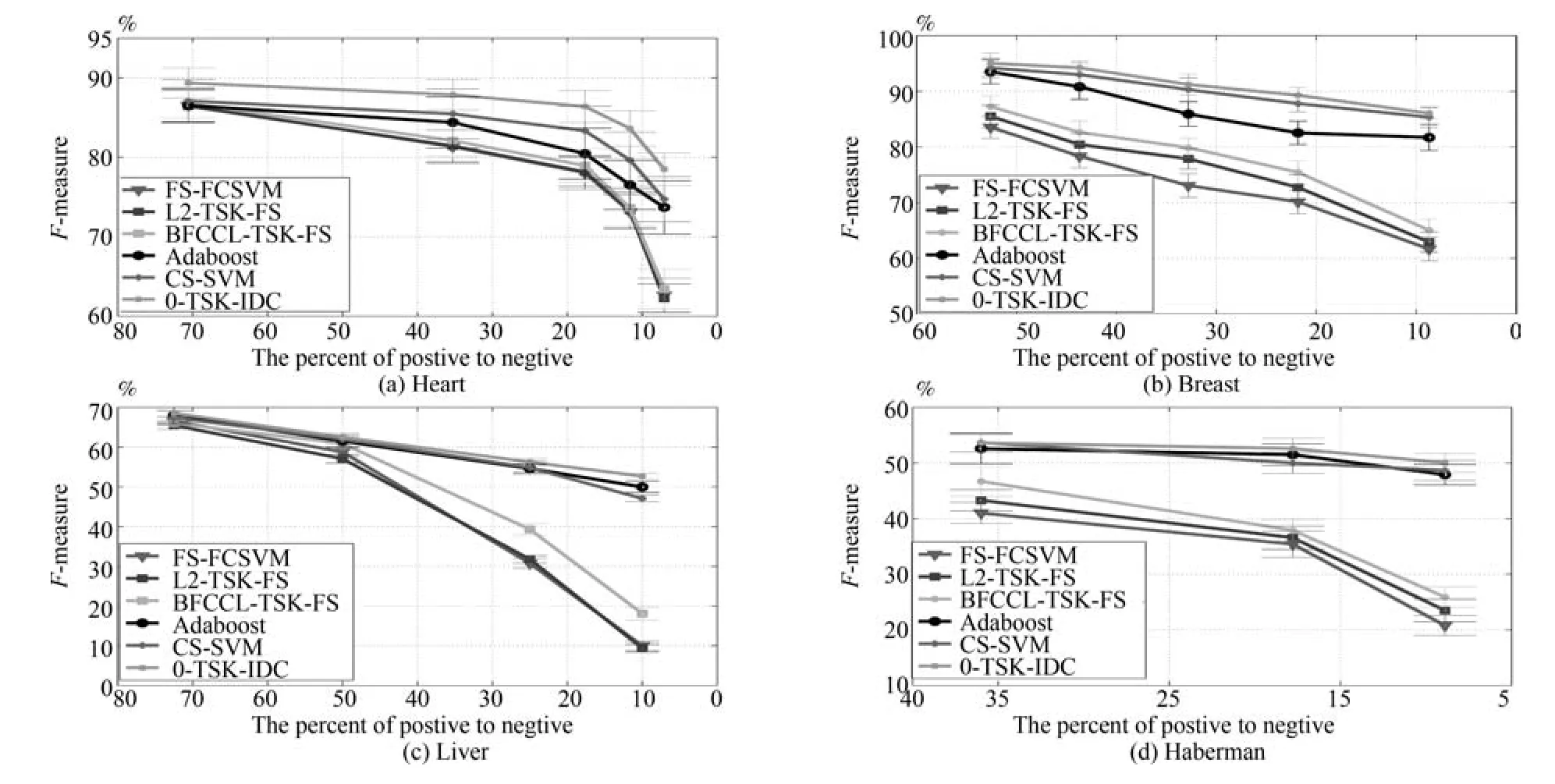
圖10 UCI醫學集上不同算法的F-measure比較Fig.10 F-measure and its standard deviation comparison of 0-TSK-IDC and other algorithms on UCI dataset

為了進一步考察在真實數據集上0-TSK-IDC構建的模糊規則的可解釋性,圖11給出了Heart集正負類樣本數6:17、Breast集正負類樣本數75:229、Liver正負類樣本數1:4和Haberman集正負類樣本數8:45時,G-mean指標隨規則數變化的曲線.可以看出,圖9中0-TSK-IDC模糊系統識別率最高時所需的模糊規則數分別是7、12、7和6.模糊系統的特點是建立分類性能和模糊規則數之間的平衡,通常情況下規則數越少的模糊系統其可解釋性越強,圖11的實驗結果可以說明從規則數角度看0-TSK-IDC模糊系統具有高度的可解釋性.

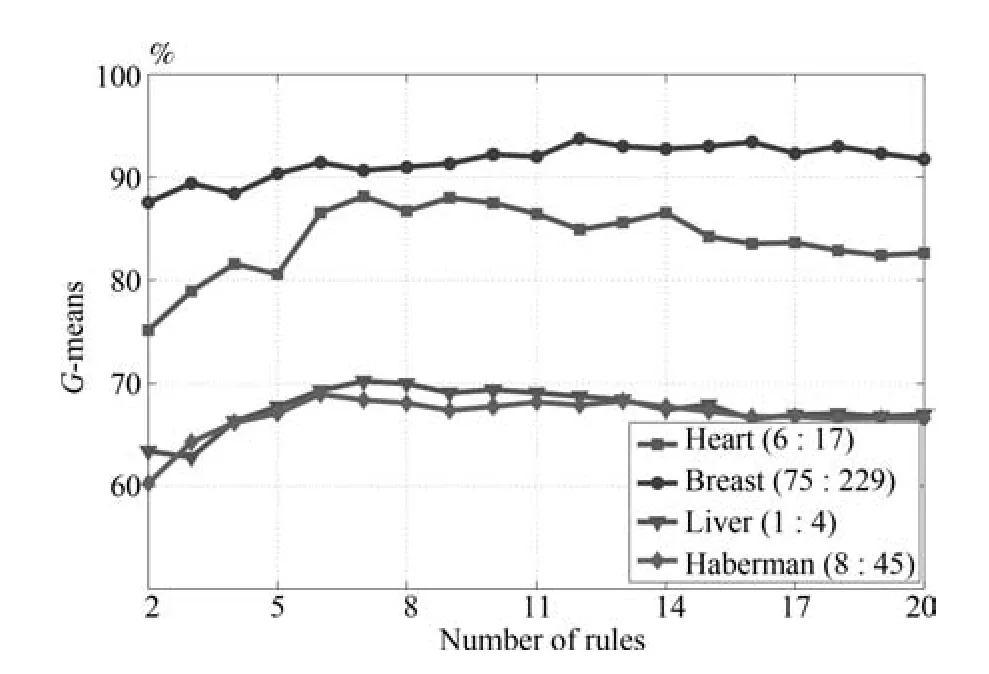
圖11 UCI醫學集上G-mean隨規則數變化的示意圖Fig.11 G-mean with the different fuzzy rules on UCI databases

5 結論

本文提出的0-TSK-IDC模糊系統利用BFCCL算法進行模糊規則前件參數的學習,使基于聚類中心競爭機制和概率模型的聚類算法在類別不平衡的空間劃分中表現出了清晰性和可解釋性;0-TSKIDC模糊系統在模糊規則后件參數的學習中,使用了“大間隔”的機制并設置少數類到分類面的距離大于多數類到分類面的距離,從而使得0-TSK-IDC具有較強的泛化能力.本文的主要貢獻可以歸納為:1)建立一種利用概率模型改進模糊系統的框架;2)提出了一種利用聚類模糊系統解決不平衡分類問題的方法.另外,0-TSK-IDC模糊系統亦可處理類別平衡的分類問題,只要設置式(23)和(24)中參數v為0即可.對于多分類問題,0-TSK-IDC可以采用類似于SVM 方法,用類別組合的方式來實現.應當指出,本文對0-TSK-IDC模糊系統能否有效解決大樣本等問題沒有進行深入探討,當樣本容量極大時,若從聚類速度和二次規劃求解角度而言,0-TSK-IDC仍面臨進一步提高實用性的挑戰,這將作為我們近期的研究重點.

1 Richardson J,Korniak J,Reiner P D,Wilamowski B M.Nearest-neighbor spline approximation(NNSA)improvement to TSK fuzzy systems.IEEE Transactions on Industrial Informatics,2016,12(1):169?178

2 Deng Z H,Cao L B,Jiang Y Z,Wang S T.Minimax probability TSK fuzzy system classi fi er:a more transparent and highly interpretable classi fi cation model.IEEE Transactions on Fuzzy Systems,2015,23(4):813?826

3 Jia Li,Yang Ai-Hua,Qiu Ming-Sen.Research on multisignal based neuro-fuzzy Hammerstein-Wiener model.Acta Automatica Sinica,2013,39(5):690?696(賈立,楊愛華,邱銘森.基于多信號源的神經模糊Hammerstein-Wiener模型研究.自動化學報,2013,39(5):690?696)

4 Liu Y J,Tong S C,Chen C L P,Li D J.Neural controller design-based adaptive control for nonlinear MIMO systems with unknown hysteresis inputs.IEEE Transactions on Cybernetics,2016,46(1):9?19

5 Cheng W Y,Juang C F.A fuzzy model with online incremental SVM and margin-selective gradient descent learning for classi fi cation problems.IEEE Transactions on Fuzzy Systems,2014,22(2):324?337

6 Jiang Y Z,Chung F L,Ishibuchi H,Deng Z H,Wang S T.Multitask TSK fuzzy system modeling by mining intertask common hidden structure.IEEE Transactions on Cybernetics,2015,45(3):534?547

7 Liu Y J,Tong S C.Adaptive fuzzy control for a class of unknown nonlinear dynamical systems.Fuzzy Sets and Systems,2015,263:49?70

8 Wong S Y,Yap K S,Yap H J,Tan S C,Chang S W.On equivalence of FIS and ELM for interpretable rule-based knowledge representation.IEEE Transactions on Neural Networks and Learning Systems,2015,26(7):1417?1430

9 Leski J M.TSK-fuzzy modeling based onε-insensitive learning.IEEE Transactions on Fuzzy Systems,2005,13(2):181?193

10 Leski J M.Fuzzy(c+p)-means clustering and its application to a fuzzy rule-based classi fi er:toward good generalization and good interpretability.IEEE Transactions on Fuzzy Systems,2015,23(4):802?812

11 Fern′andez A,del Jesus M J,Herrera F.On the 2-tuples based genetic tuning performance for fuzzy rule based classi fi cation systems in imbalanced data-sets.Information Sciences,2010,180(8):1268?1291

12 Fern′andez A,del Jesus M,Herrera F.Hierarchical fuzzy rule based classi fi cation systems with genetic rule selection for imbalanced data-sets.International Journal of Approximate Reasoning,2009,50(3):561?577

13 Ramentol E,Caballero Y,Bello R,Herrera F.SMOTERSB?:a hybrid preprocessing approach based on oversampling and undersampling for high imbalanced data-Sets using SMOTE and rough sets theory.Knowledge and Information Systems,2012,33(2):245?265

14 L′opez V,Fern′andez A,del Jesus M,Herrera F.A hierarchical genetic fuzzy system based on genetic programming for addressing classi fi cation with highly imbalanced and borderline datasets.Knowledge Based Systems,2013,38:85?104

15 Galar M,Fern′andez A,Barrenechea E,Herrera F.EUSBoost:enhancing ensembles for highly imbalanced data-sets by evolutionary undersampling.Pattern Recognition,2013,46(12):3460?3471

16 Chawla N V,Bowyer K W,Hall L O,Kegelmeyer W P.SMOTE:synthetic minority over-sampling technique.Journal of Arti fi cial Intelligence Research,2002,16(1):321?357

17 Sun Y M,Kamel M S,Wong A K C,Wang Y.Costsensitive boosting for classi fi cation of imbalanced data.Pattern Recognition,2007,40(12):3358?3378

18 Tang Y C,Zhang Y Q,Chawla N V,Krasser S.SVMs modeling for highly imbalanced classi fi cation.IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2009,39(1)281?288

19 Deng Z H,Jiang Y Z,Chung F L,Ishibuchi H,Wang S T.Knowledge-leverage-based fuzzy system and its modeling.IEEE Transactions on Fuzzy Systems,2013,21(4):597?609

20 Zhu L,Chung F L,Wang S T.Generalized fuzzy C-means clustering algorithm with improved fuzzy partitions.IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2009,39(3):578?591

21 Deng Z H,Choi K S,Chung F L,Wang S T.Enhanced soft subspace clustering integrating within-cluster and betweencluster information.Pattern Recognition,2010,43(3):767?781

22 Glenn T C,Zare A,Gader P D.Bayesian fuzzy clustering.IEEE Transactions on Fuzzy Systems,2015,23(5):1545?1561

23 Jiang Yi-Zhang, Deng Zhao-Hong, Wang Shi-Tong.Mamdani-Larsen type transfer learning fuzzy system.Acta Automatica Sinica,2012,38(9):1393?1409(蔣亦樟,鄧趙紅,王士同.ML型遷移學習模糊系統.自動化學報,2012,38(9):1393?1409)

24 Azeem M F,Hanmandlu M,Ahmad N.Generalization of adaptive neuro-fuzzy inference systems.IEEE Transactions on Neural Networks,2000,11(6):1332?1346

25 Deng Z H,Choi K S,Chung F L,Wang S T.Scalable TSK fuzzy modeling for very large datasets using minimalenclosing-ball approximation.IEEE Transactions on Fuzzy Systems,2011,19(2):210?226

26 Hall L O,Goldgof D B.Convergence of the single-pass and online fuzzy C-means algorithms.IEEE Transactions on Fuzzy Systems,2011,19(4):792?794

27 Meyn S P,Tweedie R L.Markov Chains and Stochastic Stability.London:Springer,1993.

28 Nesterov Y.Introductory Lectures on Convex Optimization:A Basic Course.US:Springer,2004.

29 Vapnik V N.Statistical Learning Theory.New York:Wiley,1998.

30 Ni T G,Chung F L,Wang S T.Support vector machine with manifold regularization and partially labeling privacy protection.Information Sciences,2015,294:390?407

31 UCI database[Online],available:http://www.ics.uci.edu/.

32 Juang C F,Chiu S H,Shiu S J.Fuzzy system learned through fuzzy clustering and support vector machine for human skin color segmentation.IEEE Transactions on Systems,Man,and Cybernetics-Part A:Systems and Humans,2007,37(6):1077?1087

33 Wang S,Yao X.Multiclass imbalance problems:analysis and potential solutions.IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2012,42(4):1119?1130

34 Masnadi-Shirazi H,Vasconcelos N,Iranmehr A.Costsensitive support vector machines.Journal of Machine Learning Research,2012,arXiv:1212.0975

35 Bezdek J C.A physical interpretation of fuzzy ISODATA.IEEE Transactions on Systems,Man,and Cybernetics,1976,SMC-6(5):387?389

36 Sun Z B,Song Q B,Zhu X Y,Sun H L,Xu B W,Zhou Y M.A novel ensemble method for classifying imbalanced data.Pattern Recognition,2015,48(5):1623?1637

37 Parambath S A P,Usunier N,Grandvalet Y.Optimizing F-measures by cost-sensitive classi fi cation.In: Proceedings of Advances in Neural Information Processing Systems 27.Montreal,Canada:Curran Associates,Inc.,2014.2123?2131