極限教學的方法研究

許亞鵬

(山西職業技術學院，山西 太原 030006)

一、極限在高等數學中的地位

極限是高等數學中一個極其重要的概念，是高等數學中微分學和積分學的理論基礎。高等數學的研究對象是函數，而研究方法卻是極限，極限和極限的思想貫穿了微積分的始終。導數定義和積分定義都是建立在極限概念基礎上的。極限能夠反映事物變量與已知量的無限接近，利用已知量可對變量的終極值進行反映。微積分的形成是人們深入理解極限思想的重要產物。高等數學之所以讓很多學生感到難以掌握和理解，根本原因是對極限的含義及計算沒有掌握，因此，正確理解和掌握極限的概念及計算是學好高等數學的關鍵。所以，作為教師非常有必要對函數的極限的教學作深入的思考和研究。

二、極限教學方法研究

(一)通過實例認識極限

極限的定義較為抽象，是公認的難點。對于數學基礎薄弱的高職學生來說，理解函數極限的分析性定義無疑是很困難的。學生的認識模式還處于初等數學學習的認識模式，而認識極限概念需要學生的認識模式從有限向無限轉變。直接進行內容講解，學生很難真正理解。因此教師應適當選取一些生活中常見的實例，激發學生探究的興趣。弱化極限分析形式的定義，適當采用通俗易懂的語言讓學生理解極限的內涵，接受簡單而特殊的函數即數列極限的描述性定義。

如用《莊子.天下篇》中的“一尺之錘，日去其半，萬世不竭”和古代數學家劉徽的割圓術思想，可以使學生對極限的思想形成感性認識，進而深刻理解極限思想。

再如，通過對下列三個無窮數列{an}進行觀察，并自主探究當項數n無限增大時，項的變化趨勢。

通過對上述三個數列的觀察，讓學生用自己的語言進行歸納，得出：數列的項an隨著項數n的無限增大在向一個確定的常數無限接近。通過學生的回答教師進行歸納性的總結，很自然地引出數列極限的描述性定義：如果當n無限增大時，數列an能夠無限接近于一個確定的常數A,那么A就叫做數列an的極限。使得學生對數列極限的定義從感性認識逐步上升到理性認識。

在學生理解并掌握了數列極限的定義之后，再來學習一般函數的極限，通過二者的區別與聯系,使學生真正掌握極限的內涵。這種先易后難，循序漸進的學習模式，符合高職學生的認識規律。

(二)滲透數學文化，提升學習極限的興趣

大部分高職學生缺乏學習數學的自信，缺乏學習的主動性，甚至對于學習數學有一種抗拒心理。在這種情形下，對于他們來說學習銜接性很強的高等數學是比較困難的。函數極限作為高等數學課程中第一節的內容，提升學生的興趣，使學生更好地掌握極限的內容尤為關鍵。

如引入斐波那契數列講解數列極限，可以極大地提升學生學習熱情和學習主動性。同時對學生進行數學文化的滲透，使學生不僅掌握了數學知識，更培養和提升了學生的數學素養。

再如，在極限教學中邀請學生參與互動游戲：十秒加數。游戲要求學生在十秒之內將以下兩組數的數字求和完成。

1+2+2+4+7+13+21+34+55+89=

34+44+89+144+233+377+610+987+1597=

學生對該游戲表現出濃厚的興趣，積極參與。在進行完該游戲后，請學生思考這些數字有什么規律，分組討論，合作探究，旨在培養學生的觀察問題、分析問題的能力。在學生討論后教師對題目中的數字進行講解，加深學生對斐波那契數的理解。

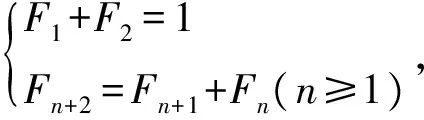
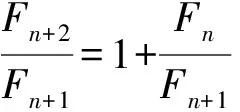
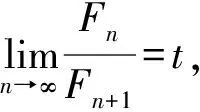
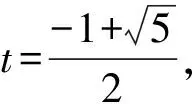
通過該部分內容的學習，使得同學們深刻地領悟到了數學來源于生活，而又服務于生活，數學與人類的生活密切相關，這種生活中的數學能極大地提升學生學習數學的積極性。

在高等數學的教學中，數學文化的學習，數學素養的提升是其中的重要方面。數學素養可以訓練并提升學生的邏輯思維能力，使他們在遇到紛繁復雜的工作時，能夠思路清晰、條理分明，有條不紊地完成；同時也可以培養學生的抽象思維能力，面對生活中錯綜復雜的事情，能抓住主要矛盾和矛盾的主要方面，高效解決問題；還有助于培養學生認真細致、一絲不茍的習慣。

(三)借助數學軟件，突破極限教學難點

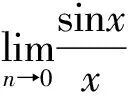
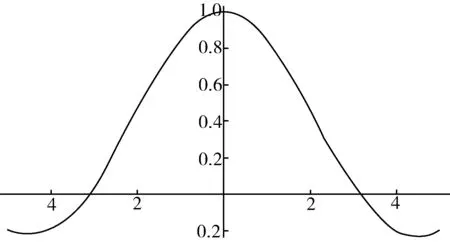
通過對圖形的分析，使學生能形象直觀地觀察到當自變量無限趨近于0時，函數值在無限地向常數1逼近。

通過數學軟件，可以讓學生高效地學習高等數學，同時學生在對數學軟件的應用和探索中獲得專業所需要的數學基礎知識。將數學軟件引入高職數學課堂教學，不僅是教學改革的需要，也是適應高職院校培養目標的需要，是培養學生分析問題，觀察問題，解決問題的能力以及應用數學知識解決實際問題的嘗試。數學軟件在高職數學課堂的應用能夠增強學習數學的興趣，豐富和加深對數學本質的認識，促進數學學習價值觀的轉變，不再認為數學是一門枯燥無味的課程。使學生能夠深切感受數學的無窮魅力。

(四)認真分析，掌握函數極限的求法

極限的計算對于大部分高職學生來說也是一個難點，因此教師有必要對函數極限的求法進行探討。求函數極限的方法雖然較多，但各有其相應的適用范圍。對于某個具體的函數求極限問題，我們需采用合適的方法去解題。下面是一些求函數極限的常用方法。

(1)能代則代

當所求函數極限式的分子和分母的極限不同時為零或不同時為∞，則可以直接利用極限的四則運算法則后，直接代入求出極限。

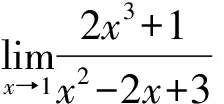
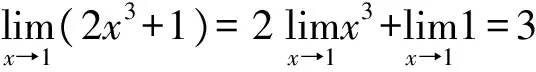
所以可以采用能代則代這種求極限的方法。

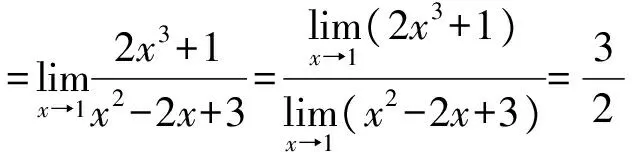
(2)分子、分母約去非零因子

分子、分母約去非零因子，此法適合于自變量在某一趨向下分子、分母的極限同時為0的情形。

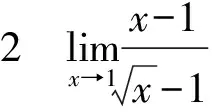
分析：因為當x→1時，分子、分母的極限都是0，不能直接使用商的極限運算法則。

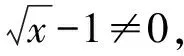
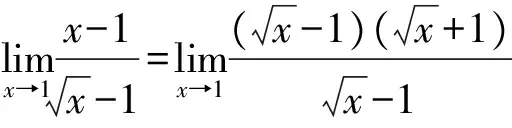
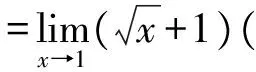
=2

(3)分母有理化

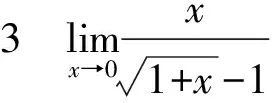
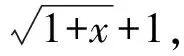
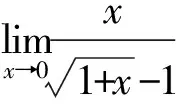
(4)無窮小量分出法

適用于分子、分母是x的一元高次多項式，且分子、分母的極限同時為∞。

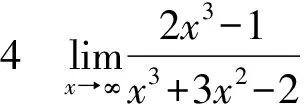
分析：所給函數中，注意到當x→∞時，分子、分母也同時趨于無窮大，不能直接應用商的極限運算法則，因此，需首先對函數進行初等變形，即分子、分母同時除以x的最高次冪，可以將無窮小量分出來，然后再根據極限運算法則求出極限。

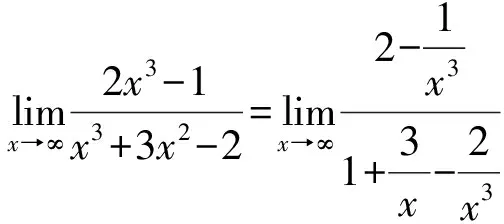
上述歸納了函數極限的一些常用求解方法，在做題的過程中，學生應首先觀察函數極限的特點，然后根據不同的情況采取不同的方法，函數極限的求解方法還有很多，要求學生在學習中逐步探索，不斷完善。

總之，為了調動學生學習數學的積極性。首先，教師應該根據函數極限與學生所學專業以及現實生活，選取一些學生比較感興趣的話題進行課題切入，提高學生對教學內容的興趣；其次，教師應該對課堂教學環節進行合理的設置，鼓勵學生勤于思考，主動學習；最后，教師應該對課堂中的小組討論和總結，進行必要的掌控，盡量讓每一個同學都參與進來，并對學生的參與進行及時的鼓勵。

[1]江濤.淺談數列極限的計算方法[J].科技信息.

[2]新編高等數學(理工類)[M].北京：北京交通大學出版社，2015.

[3]華東師范大學數學系.數學分析(上)[M].上海：高等教育出版社，2001.

[4]張韻華,王新茂.Mathematica7實用教程[M].中國科學技術大學出版社，2011.