應用型高校數學專業實驗課程的改革實踐
——以呂梁學院為例

李香林,高靈芝

(呂梁學院 數學系,山西 離石 033001)

一、數學專業實驗課程改革思路

圍繞“重基礎、強技能、多實踐、求創新”人才培養思路，數學實驗按照學科的發展規律和學生的認知層次進行整合和優化，將以前一門數學實驗課程內容內化在多門專業課程中，根據學科發展前沿和教師科研課題，不斷更新實驗實踐教學內容。

首先按照數學學科發展規律，系統地構建由課程內實驗—課外社會實踐—課外科研實踐—畢業論文(設計)四大類實踐課程模塊構成的實踐教學體系。

其次根據學生的認知規律分別對四大類實踐課程模塊設立由基礎性實驗/實踐(注重專業基本知識、技能和方法訓練)—綜合性、設計性實驗/實踐(注重對科學研究方法、科學探究過程的了解和體驗)—創新性實驗/實踐(注重研究能力和創新能力培養)構成的三層次實踐教學內容。

第三，層次性教學同時體現在隨著年級的升高，基礎性實驗比例減少，創新性實驗比例增加。

二、實驗課程體系設計

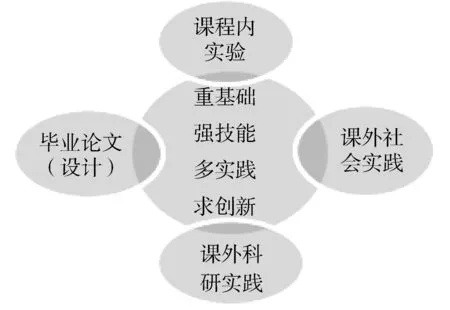
圖1 實踐教學體系

(一)實驗環境的選擇

數學實驗可以有多種軟件可選擇，最為流行通用的軟件有Maple,Matlab，Mathmatics,SPSS，SAS,C語言等。每種工具有其各自的擅長之處，Matlab、SPSS在數學實驗教學中廣泛使用。

(二)實驗內容設計

遵循實驗內容的層次性教學，將實驗內容設計成基礎性實驗—綜合性、設計性實驗-創新性實驗三個層次，在有限的時數內，選擇不同層次的實驗內容，基礎性實驗基本是簡單的命令及驗證性內容，可以讓學生看到驗證結果；綜合性、設計性實驗以解決實驗問題為主，綜合運用到所學課程內容。隨著年級的升高，專業課程的增加，實驗內容應由第1學期以基礎驗證為主，第2-4學期以設計、綜合運用為主，到第5-8學期以創新運用為主。

表1 數學專業各年級實驗課程層次圖

(三)教學過程設計

實驗教學不同于理論教學，且實驗時數較少，教學過程中可以將基礎性驗證性實驗由學生自己課下完成，設計、綜合性實驗分小組課前討論，完成建模、編程、求解，同時教師根據學生實驗過程中存在的問題進行分析修改，以幫助學生完成全部實驗。即實驗課主要以學生為主體，老師為主導進行，讓學生完整體驗數學解決實際問題的樂趣。

(四)課外社會實踐

數學專業學生需獲得4個學分的創新實踐學分，該學分不占課堂時間，其中數學建模競賽、挑戰杯比賽、行業數據分析、創新創業等活動都可以獲得相應學分。在這些活動中能運用數學實驗的思想方法將理論運用于實際生活與工作。

(五)課外科研實踐

在大一完成基礎實驗的情況下，從大二開始選拔優秀的學生參與教師科研項目。如圖像處理、信息隱藏、數據挖掘、數據分析等。同時將學生組成學習小組，開展學習活動，學習內容包括數學實驗中用到的典型算法、工具、論文寫作以及數學在各學科、行業中的最新應用等。

(六)畢業論文(設計)

畢業論文是專業學習的綜合應用，要求有創新性。在前期分層次的數學實驗學習中，學生已培養起初步的綜合性能力，在畢業論文寫作期間可以發揮創造性，獨立運用數學實驗能力解決論文或設計中的問題。

(七)課程考核

實驗課程考核圍繞課程理論的應用及自主動手能力進行。實驗課程考核主要以實驗項目報告為依據，每個實驗項目都設置了考察點，從數學理論的理解、建模、編程求解等方面考察，另外實驗報告的排版及其整體的美觀性也是考察之一。設計性、綜合性實驗以小組考察為主，每組2-3人。一般實驗課程的考核占到本門課程總成績的10%。畢業論文實踐性是考察有無實際意義的主要指標。

三、《高等代數》實驗課教學實例

高等代數是一門專業基礎課，其在實際生產生活中應用廣泛。圍繞以培養學生解決問題的能力為重點，以問題為載體,以計算機為手段,以數學軟件為工具,以學生為主體開展高等代數實驗教學。

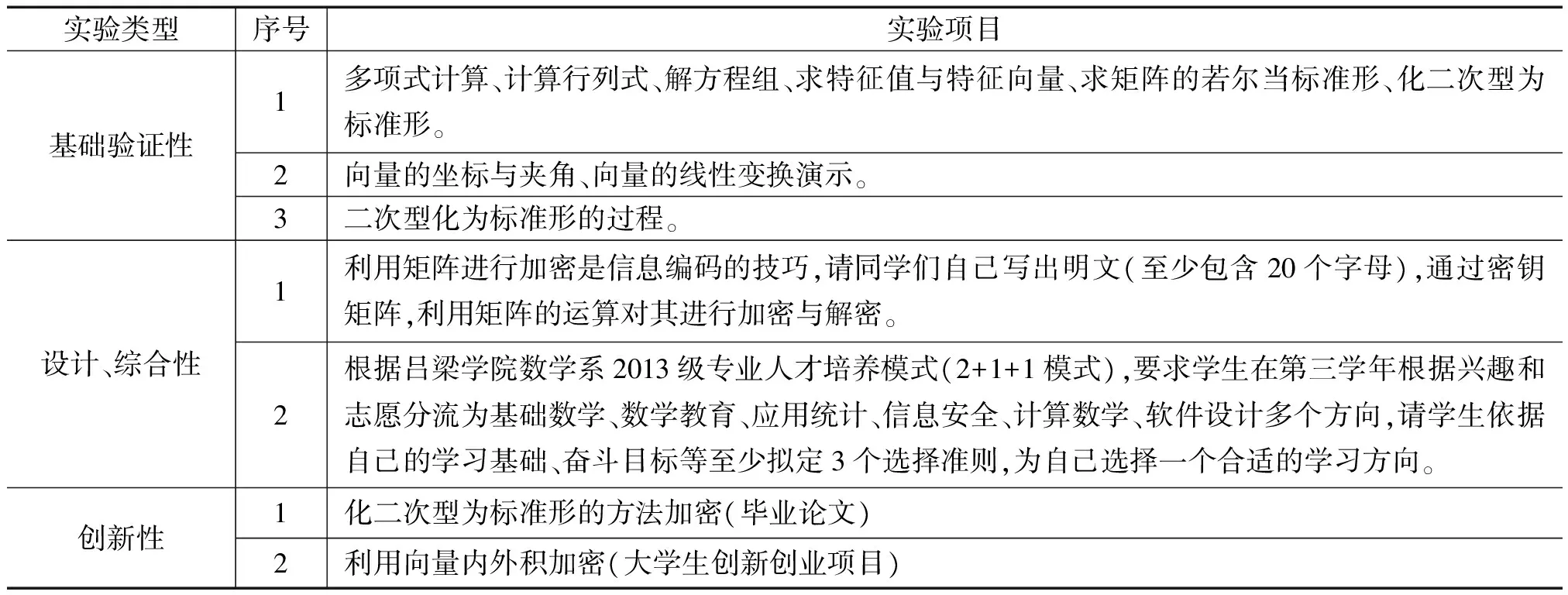
表2 高等代數實驗內容

(一)基礎性實驗

1.大量的驗證計算

矩陣在高等代數中有著特殊的地位和作用，矩陣的眾多運算，如加減法、乘法、轉置、逆矩陣、行列式、秩、特征值等相關的知識基本構成高等代數內容的骨架和血肉。Matlab 數學軟件有強大的矩陣運算功能，如多項式的相關運算(尤其是多項式的求根)、計算行列式、解方程組、求特征值與特征向量、求矩陣的若爾當標準形、化二次型為標準形等可以作為驗證性實驗內容。

教學案例1：講行列式的計算時，由于行列式的計算比較困難，需要很強的技巧性，而且計算量也大，通過命令det( )很方便得出結果。

教學案例2：講矩陣秩的計算時，需利用矩陣的初等變換把該矩陣階梯化才可求其秩，通過命令rank( )很方便得出結果，并且還可以通過矩陣的秩進一步判斷向量組的線性相關性。

2.抽象問題直觀化

高等代數具有高度抽象性使得學生學起來非常吃力。面對高度抽象的知識，除了幫助學生找到豐富的直觀背景外，還可以通過數學實驗，將諸多抽象的問題直觀化。如，在線性空間與線性變換學習中，要求學生利用數學軟件，對向量的坐標與夾角、向量的線性變換等進行演示，便于學生理解，也可激發學生的學習積極性。

實驗過程：

x=[0 1 1 0;0 0 1 1]；

subplot(2,3,1),fill([x(1,:),0],[x(2,:),0],'r')

A1=[-1,0;0,1],y1=A1*x；

subplot(2,3,2),fill([y1(1,:),0],[y1(2,:),0],'g')

A2=[1.5,0;0,1],y2=A2*x；

subplot(2,3,3),fill([y2(1,:),0],[y2(2,:),0],'g')

A3=[1,0;0,1.5],y3=A3*x；

subplot(2,3,4),fill([y3(1,:),0],[y3(2,:),0],'g')

A4=[1,0.5;0,1],y4=A4*x；

subplot(2,3,5),fill([y4(1,:),0],[y4(2,:),0],'g')

t=pi/6

A5=[cos(t),sin(t)；-sin(t),cos(t)],y5=A5*x；(%t為逆時針旋轉的角度)

subplot(2,3,6),fill([y5(1,:),0],[y5(2,:),0],'g')

實驗結果如圖3.

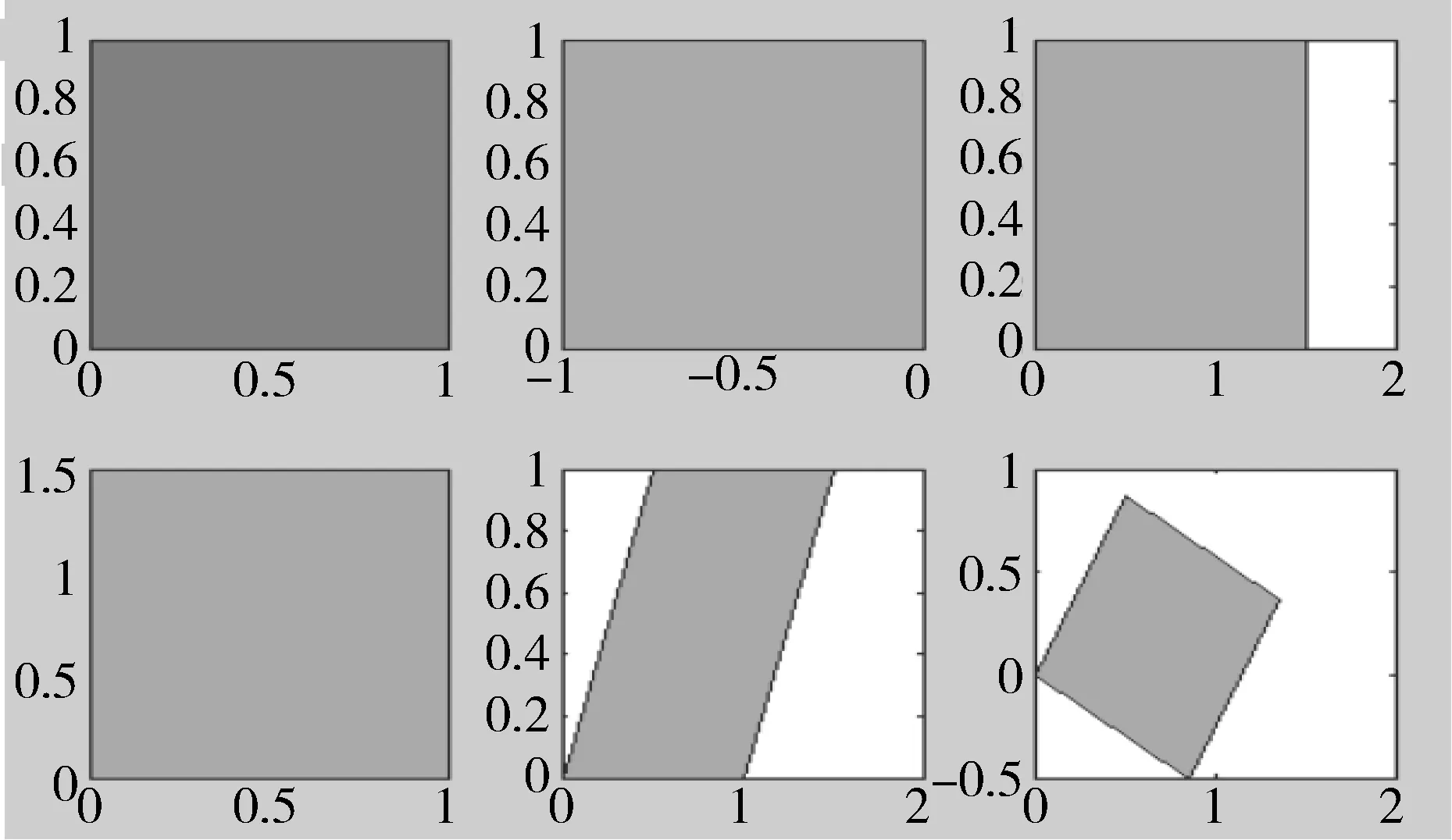
圖3 案例3實驗結果

3.知識點融會貫通

利用Matlab的繪圖功能，能清楚描繪各種圖形，利用它可以將數學知識點融會貫通。如，將二次型化為標準形的過程，其實質就是利用坐標變換，將解析幾何中所涉及的一般二次曲面方程化為標準形，這也是二次型的幾何意義所在。為此，在進行高等代數實驗時，首先繪出一般二次曲面的三維圖形；其次，繪出該二次型標準形所表示的二次曲面的三維圖形；最后，通過形象的對比、分析新舊二次曲面三維圖形的聯系與區別。這樣，不僅可以將學生所學知識點得到驗證，而且也能與解析幾何所學知識相結合，很好地做到了知識點的融會貫通。

教學案例4：作二次型z=x2-8xy-5y2與其標準形z=-7x2+3y2的三維圖形

實驗過程：

clf,clear

x=-5:0.1:5;

y=-5:0.1:5;

[X,Y]=meshgrid(x,y);

Z=X.^2-8*X*Y-5*Y.^2;(%作z=x2-8xy-5y2的三維圖形)

Z=X.^2-Y.^2;(%作z=-7x2+3y2的三維圖形)

mesh(X,Y,Z);

實驗結果如圖4和圖5.

(二)綜合性實驗

綜合性實驗是指實驗內容涉及本課程的綜合知識或相關課程知識，通過運用綜合實驗方法、實驗手段，對學生實驗技能進行的綜合訓練，培養學生的綜合分析能力、實驗動手能力、數據處理以及查閱資料的能力。

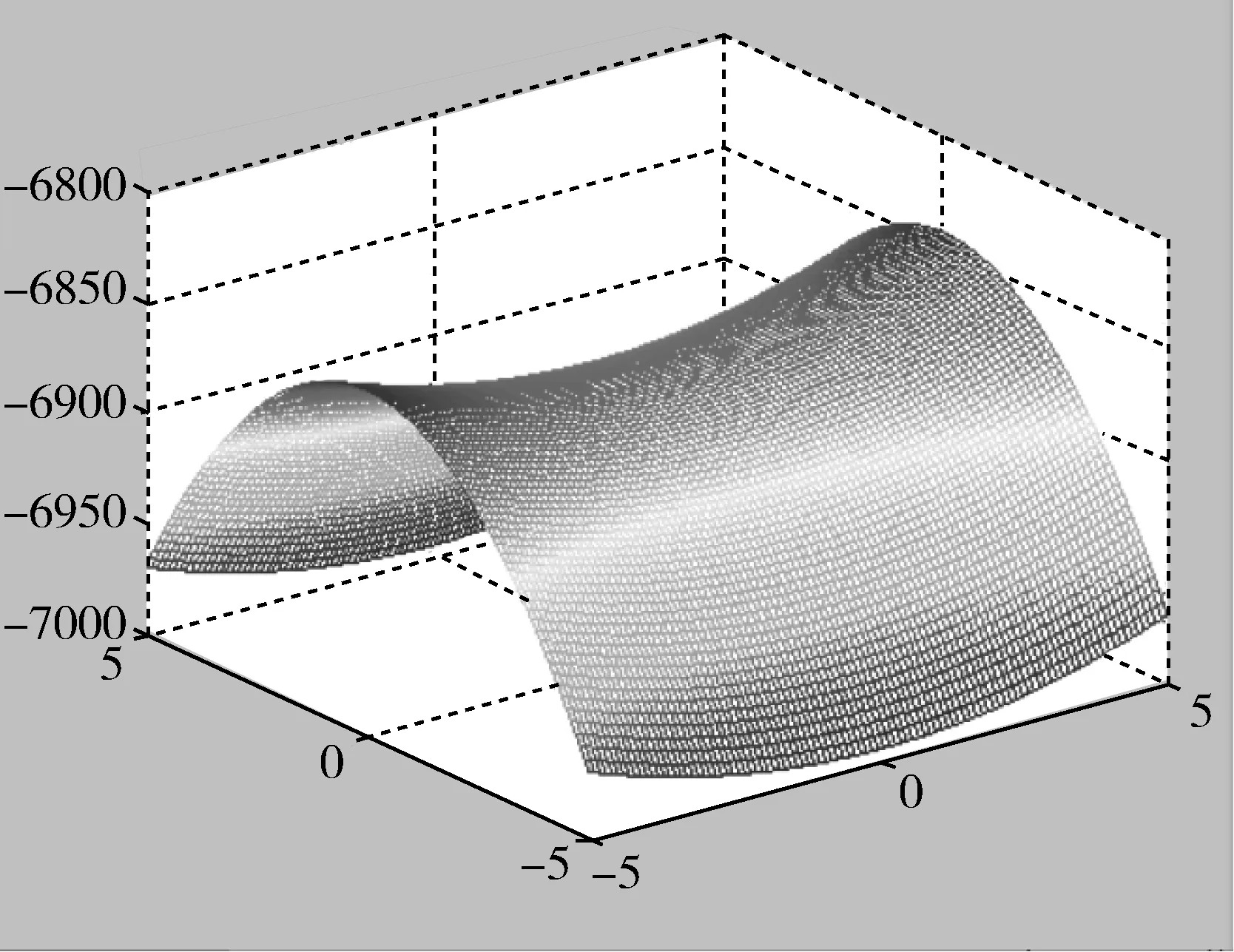
圖4 z=x2-8xy-5y2的三維圖

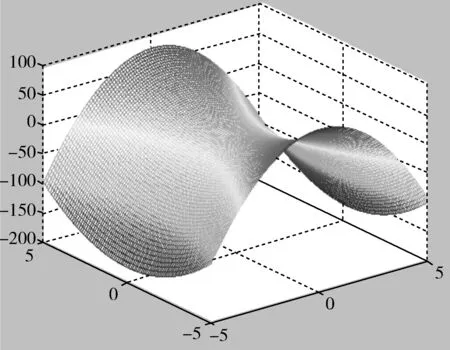
圖5 z=-7x2+3y2的三維圖

1.數學建模思想滲透

數學模型是數學知識的載體，把數學建模的思想滲透到高等代數實驗的教學中，可將所學高等代數知識與實際問題有機地結合，達到理論與實踐的統一。培養學生應用數學知識建立數學模型，解決實際問題的能力。

2.教學方法

實驗教學是培養學生數學建模的一個重要手段，教師引導學生從現實生活中抽象出數學問題，再運用高等代數以及其它學科的相關理論知識建立數學模型，并通過數學軟件對該模型進行求解與結果的驗證，最終又將該結果應用到實踐中去。

教學案例5：隨著信息技術的迅猛發展，信息安全得到了更多的關注。利用矩陣進行加密是信息編碼的技巧,請同學們自己寫出明文(至少包含20個字母)，通過密鑰矩陣，利用矩陣的運算對其進行加密與解密。

教學案例6：根據呂梁學院數學系2013級專業人才培養模式(2+1+1模式)，要求學生在第三學年根據興趣和志愿分流為基礎數學、數學教育、應用統計、信息安全、計算數學、軟件設計幾個方向，請學生依據自己的學習基礎、奮斗目標等至少擬定3個選擇準則，為自己選擇一個合適的學習方向。

在這兩個實驗中，學生需要分析問題—建立模型—解決問題。這兩個實驗中，綜合應用了矩陣運算、特征值、特征向量、層次分析等不少數學理論知識。

(三)創新性實踐

實驗課上，老師不給現成的結論，而是根據學生所掌握的基礎知識、數學思想的發展等，創造問題情景，讓學生進行大量的圖形觀察、實際問題分析，從直觀想象進入到發現、猜想和歸納，然后進行驗證及理論證明。學生通過自己的探索實踐對數學現象進行認真觀察、研究分析，從中發現問題并解決問題，在觀察—分析—解決問題的過程中，嘗試著用所學數學知識對這些問題進行解決與修正。鼓勵并幫助學生組團申報“大學生創新創業訓練計劃項目”，無論這些創新點是做成畢業論文，還是申報成大學生創新項目，都可以使他們感覺到學有所得，體會到數學的魅力，激發用所學知識解決實際問題的學習興趣。

教學案例7：在綜合性實驗中，對矩陣加密同學們想法很多。如改變密鑰矩陣、利用矩陣的其它運算加密、利用高等代數中化二次型為標準形的方法加密、利用向量內外積加密等等。源于同學們的這些想法，曾指導學生把“化二次型為標準形的方法加密”這一創新想法寫成了一篇畢業論文，把“利用向量內外積加密”這一創新想法申報成了省級的大學生創新項目。

高等代數中基礎驗證性實驗簡單、易操作，綜合性實驗運用數學建模的思想方法對實際問題建模求解，創新性實驗發揮學生的主觀能動性，力求創新。實驗教學整體設計做到抽象與具體、理論與實踐的統一，達到了課程大綱教學目標。

四、結語

數學實驗可以將數學抽象問題直觀化，數學建模思想融入數學實驗教學是其著力點。隨著人工智能、虛擬現實技術的發展，數學實驗課程的改革將是長期的，實驗項目內容的不斷更新將使得數學教學內容越來越豐富。

[1]許建強,樂經良,胡良建.國內數學實驗開展的現狀調查大學數學[J].2010(4).

[2]章建躍.數學實驗的育人價值[J].中國數學教育，2016(4).

[3]喻平.數學實驗的教育價值[J].江蘇教育，2015(1).

[4]張華,張玲.數學實驗的教學內容及模式的探討[J].天津城市建設學院學報，2011(4).

[5]馬元魁.培養大學生科研創新能力的數學實驗課程教學改革探索[J] .教育教學論壇，2015(12).