基于人群搜索算法的多伺服電機協同控制研究

郗欣甫， 黃文軍， 李培波， 孫以澤

(東華大學 機械工程學院，上海 201620)

基于人群搜索算法的多伺服電機協同控制研究

郗欣甫， 黃文軍， 李培波， 孫以澤

(東華大學 機械工程學院，上海 201620)

針對多伺服電機協同控制系統，以4臺電機為控制對象，通過分析協同控制原理和特點，結合多電機協同控制系統參數時變、負載擾動等因素，與常規PID(proportion integration differentiation)相融合，設計了基于人群搜索算法的SOA_PID控制器，建立了SOA_PID控制器的控制結構，采用Matlab/Simulink搭建仿真試驗平臺，建立伺服電機仿真模型．系統仿真結果表明，基于人群搜索算法的SOA_PID控制器能有效地提高多伺服電機同步控制性能，收斂精度高，健壯性較好，抗擾動能力強，相對于常規PID控制，其能更好地實現多伺服電機的協同控制．

多伺服電機協同； 人群搜索算法(SOA)； PID尋優； 遺傳算法

近年來，隨著多電機伺服系統的發展，多電機協同控制技術越來越廣泛地應用于紡織、印刷、包裝等行業的高精度、高速度傳動系統中．在現實工業活動中，多伺服電機的同步性能會因各軸的驅動特性不匹配、負載擾動和電機自身參數等因素而惡化[1]．如何保證多電機間的高精度協同運動是多伺服電機協同控制系統的關鍵技術，協同控制算法的優劣直接影響復雜設備的功能和產品制造的質量[2]．

人群搜索算法(SOA)是一種對人的隨機搜索行為進行分析的算法，借助腦科學、認知科學、心理學、人工智能、多Agents系統、群體智能等的研究成果，分析研究人作為高級Agent的不確定性推理行為、利己行為、利他行為、預動行為和自組織聚集行為，對行為進行建模，分析得出搜索方向和步長[3]．SOA立足傳統的直接搜索算法，結合進化思想，結構簡單．將SOA與常規PID(proportion integration differentiation)算法相融合，能有效解決常規PID控制器不能在線參數整定和易受負載擾動的問題．為了充分利用SOA的搜索和進化能力[4]，本文設計了SOA_PID控制器．

多伺服電機協同控制系統具有多變量、復雜時變、強耦合的特性，常規的控制算法顯然不能達到高精度、高速度的控制要求．文獻[5]采用模糊PID控制算法來實現多伺服電機協同控制，雖然模糊算法對時變及滯后特性、多輸入多輸出的復雜系統具有良好的控制效果，但模糊控制規則過多，規則的制定過程比較依賴專家經驗，無自適應和自學習能力，不能實現智能化的控制過程．文獻[6]采用神經網絡控制算法來實現多伺服電機協同控制，神經網絡控制不依賴被控對象精確的數學模型，具有自學習和自適應能力，然而計算過程較為復雜，比較依賴硬件性能．綜合考慮上述控制算法的不足，本文所設計的SOA_PID控制器，立足于SOA簡單快速的搜索原理，剔除了復雜的計算過程，本算法首次與多伺服電機協同控制系統融合，具有很大的研究意義．

1 多伺服電機協同控制

在多伺服電機協同控制系統中，各個電機之間保持相應的耦合關系，按照一定的傳動比，實現電機速度和位置的協同．當任意一臺電機受到擾動或自身參數發生變化時，為了保持相互之間的協同，與它保持耦合關系的電機隨之發生變化．本文以4臺電機為研究對象，控制方案如圖1所示．

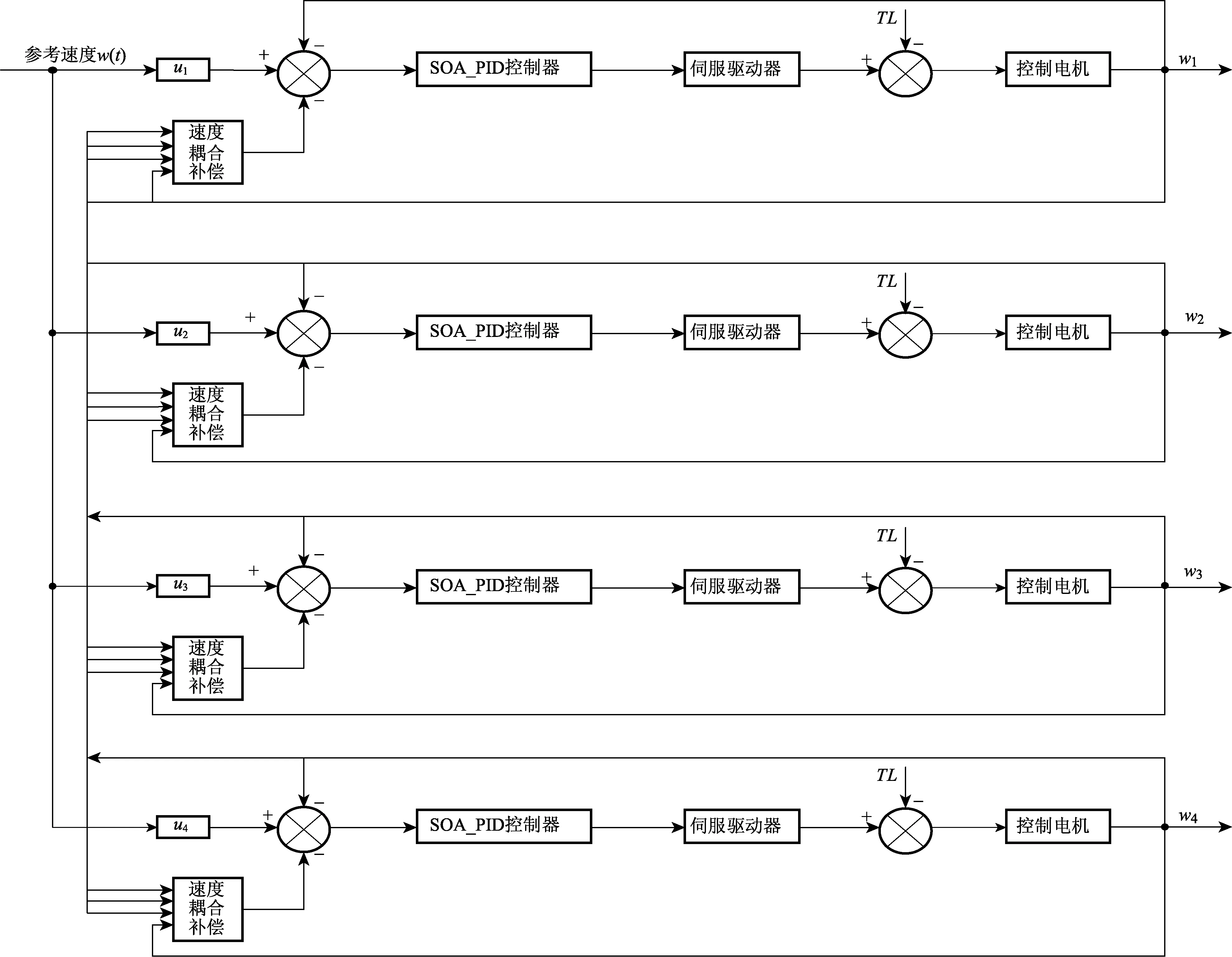
圖1 基于SOA_PID控制器的多伺服電機協同控制系統控制結構Fig．1 Structure of the multi-servomotor synchronous control system based on SOA_PID controller

當系統處于擾動狀態，將受擾動電機與耦合電機的速度反饋分別作差，然后將得到的偏差信號作為該電機的速度補償信號，通過速度耦合補償器，平衡擾動產生的偏差．速度耦合補償器結構如圖2所示．

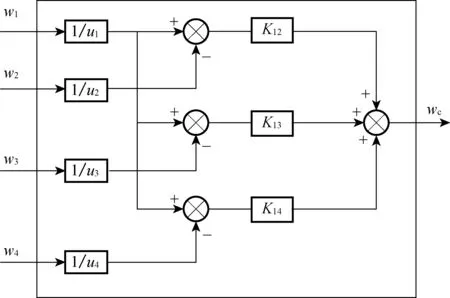
圖2 速度耦合補償器結構示意圖Fig．2 Structure of the speed coupling compensative controller

對于本文所研究的4電機協同控制系統，假定系統中各電機之間的速度耦合關系為w1/u1=w2/u2=w3/u3=w4/u4，并定義第i臺電機的跟蹤誤差ei(t)為

(1)

其中：ui為兩電機之間的同步耦合系數；wi(t)為第i臺電機的反饋速度；wi*(t)為第i臺電機的參考速度．

根據上述控制思想，定義第i臺電機與系統中其他電機的同步誤差分別為ei1(t)，ei2(t)，ei3(t)，

ei4(t)，則

(2)

為了保證系統中各個電機能穩定地處于同步狀態，通過不斷采集同一時刻不同光電編碼器信號，不斷地對各電機的反饋速度作差比較，通過速度耦合補償器補償速度，并采用SOA_PID控制器對同步誤差進行調節，使每臺電機的同步誤差快速穩定收斂，系統最終趨于穩態，達到同步控制的目的．

2 多伺服電機協同控制算法及控制結構

2．1 SOA搜索進化機制

SOA通過觀察分析人在社會生活中的隨機搜索行為，將其抽象成數學語言和數學模型，即在連續空間范圍的搜索行為中，次優解可能存在于較優解狀態的周圍，較優解狀態的鄰域內可能是最優解狀態所在．所以，當目前解處在較優狀態時，搜索行為應在較小鄰域內進行；當目前解狀態較差時，應擴大搜索范圍，在較大鄰域內搜索，并將較優解的狀態替代目前解的較差狀態．

基于SOA的進化和搜索特性，結合多伺服電機協同控制中存在的參數時變等現象，本文將SOA與PID控制器相結合，設計了SOA_PID控制器，如圖3所示．其中，ASR為調節器，PWM為輸出的控制信號，W_I(t)為實際輸出速度.

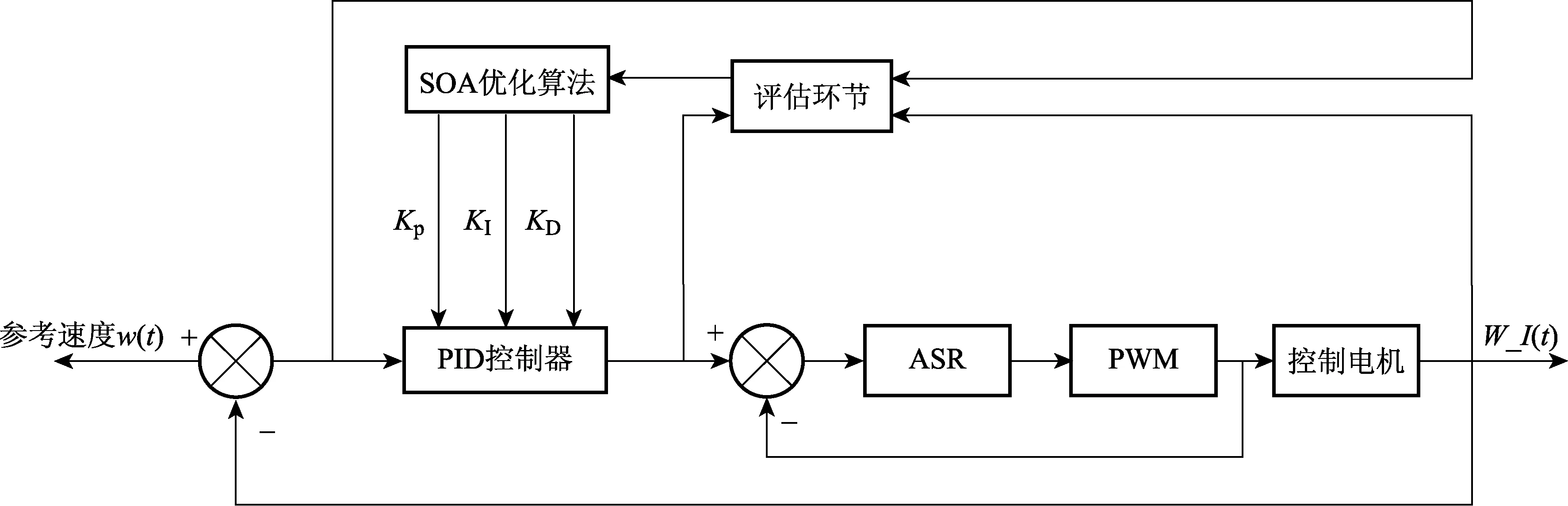
圖3 SOA_PID控制器結構圖Fig．3 Structure of the SOA_PID controller

2．2 搜索步長算法

根據SOA搜索原理，在眾多函數中，搜索步長模糊變量選用高斯隸屬函數[4]，如式(3)所示.

uA(x)=exp[-(x-u)2/2δ2]

(3)

其中：uA為高斯隸屬度；x為種群狀態輸入；u和δ均為隸屬函數參數．設定最小隸屬度umin=0．011 1．

在不確定推理過程中，將目標函數值采用依次遞減的順序排列，并使目標函數的模糊變量“小”采用線性隸屬函數，即

(4)

uij=rand(ui， 1)，j=1， 2， …，N

(5)

其中： 目標函數值i的隸屬度為ui；uij為目標函數值i在j維連續搜索空間的隸屬度；Ii為種群函數值的狀態編號；M為種群數目；N為搜索空間維數．

根據上述不確定性推理條件得出的隸屬度uij，從而可得出搜索行為所需的搜索步長為

(6)

其中：αij為j維連續搜索空間搜索步長；δij為搜索步長模糊變量參數，即

δij=p·abs(xmin-xmax)

(7)

(8)

其中：xmin表示子群中最小函數值狀態；xmax表示同一子群中最大函數值狀態；p表示慣性權值，它與進化代數成反比，隨著進化代數增加，從最大值0．9線性遞減至最小值0．1；t和Tmax分別為當前進化次數和最大進化次數．

2．3 搜索方向算法

搜索方向算法利用搜索過程中存在的3個行為：利己行為、利他行為和預動行為，分別對3個行為進行建模，最終確定搜索方向．其中，任意第i個搜尋個體的利己方向die(t)、 利他方向dia(t)以及預動方向dip(t)分別為

die(t)=pib-xi(t)

(9)

dia(t)=gib-xi(t)

(10)

dip(t)=xi(t1)-xi(t2)

(11)

由于3個方向幾率均等，各自影響因子隨機分配，因此，采用加權平均法，并使3個方向隨機加權平均，確定搜索方向為

di(t)=sign(pdip(t)+φ1die(t)+φ2dia(t))

(12)

式(9)～(12)中：t1，t2∈{t，t-1，t-2}， {xi(t-2)，xi(t-1)，xi(t)}在t1和t2時刻的最佳狀態分別為xi(t1)和xi(t2)；第i個搜尋個體所在鄰域的歷史最佳狀態為gib；第i個搜尋個體到目前為止經歷過的最佳狀態為pib； sign(·)表示輸入矢量每一維的符號函數；影響因子φ1和φ2為在已知區間[0， 1]內被隨機選擇、均勻的實數；p為慣性權值，隨著進化代數的增加，其值呈線性遞減，最大值為0．9，最小值為0．1．

2．4 搜尋者個體狀態的更新

在確定搜索方向和步長后，狀態將被更新，即

Δxij(t+1)=αij(t)dij(t)

(13)

xij(t+1)=xij(t)+Δxij(t+1)

(14)

2．5 適應度函數的確定

取性能指標函數為

(15)

其中：e(t)為協同控制系統反饋偏差；u(t)表示SOA_PID控制器輸出值；h1和h2分別為各項權值．為了提高系統穩定性，采用懲罰控制措施實現避免超調，在運行過程中，當系統產生超調時，選取的最優指標為

e(t)<0

(16)

其中：h3為新添加項權值，且h3?h1，設置h1=0．999，h2=0．001，h3=100．

2．6 SOA_PID算法實現

Step 0： 編碼初始化.預處理每個搜尋者個體的狀態，隨機產生一個MXN的狀態矩陣.

Step 1： 評價每一個搜尋者個體的適應度值.

Step 2： 對各個搜尋者個體的狀態與其歷史最佳狀態進行比較，如果現在的狀態更好，則將現在的狀態記錄為個體歷史最佳狀態.

Step 3： 將種群歷史最佳狀態與每個搜尋者的狀態相比較，如果現在的狀態更好，則將現在的狀態記錄為種群歷史最佳狀態.

Step 4： 對搜尋者的狀態進行更新.

Step 5： 如果未達到結束條件，則返回Step 1．

3 仿真試驗及分析

為驗證上述算法的穩定性和收斂性，進行Matlab仿真試驗．

3．1 伺服電機仿真模型

4臺電機的功率分別為4．0， 2．5， 4．0， 2．5 kW．電機的極對數Pn=4，每臺電機總的轉動慣量J=0．008 kg·m2，永磁磁通Φf=0．175 Wb，電阻R=2．875 Ω，電感L=8．5 mH．在Matlab/Simulink平臺中建立伺服電機仿模型如圖4所示．模型中UIn代表輸入電壓，TL代表負載擾動，WOut代表系統輸出轉速，電機的反電勢常數為Ke，電機的轉矩系數為Kc．

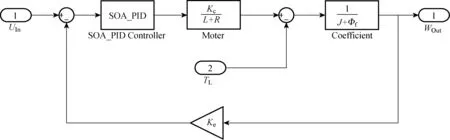
圖4 伺服電機仿真模型Fig．4 The servo-motor simulation model

3．2 Matlab仿真分析

SOA_PID控制器中種群規模為30，最大迭代次數為100，設定系統中每臺電機的轉速w1=2w2=3w3=4w4=720 rad/s，采用圖1所示的控制結構，在系統穩定運行之后，仿真結果如圖5所示．

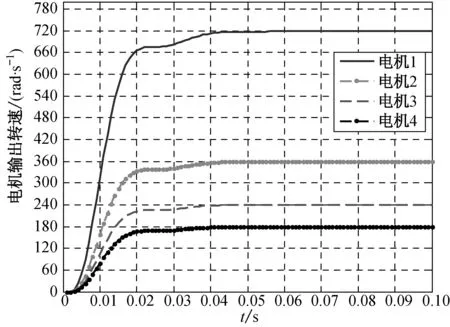
(a) 輸出轉速

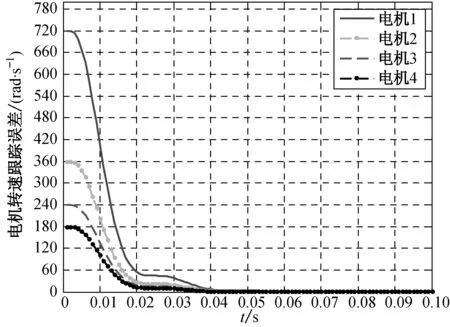
(b) 跟蹤誤差

從圖5可以看出，4臺電機以耦合速度同步運行時，在啟動階段，4臺電機均能在很快的時間內到達目標轉速，且各自的轉速跟蹤誤差均能快速穩定收斂．調節時間較短，超調量很小，表明系統具有較好的收斂性，且收斂精度高．

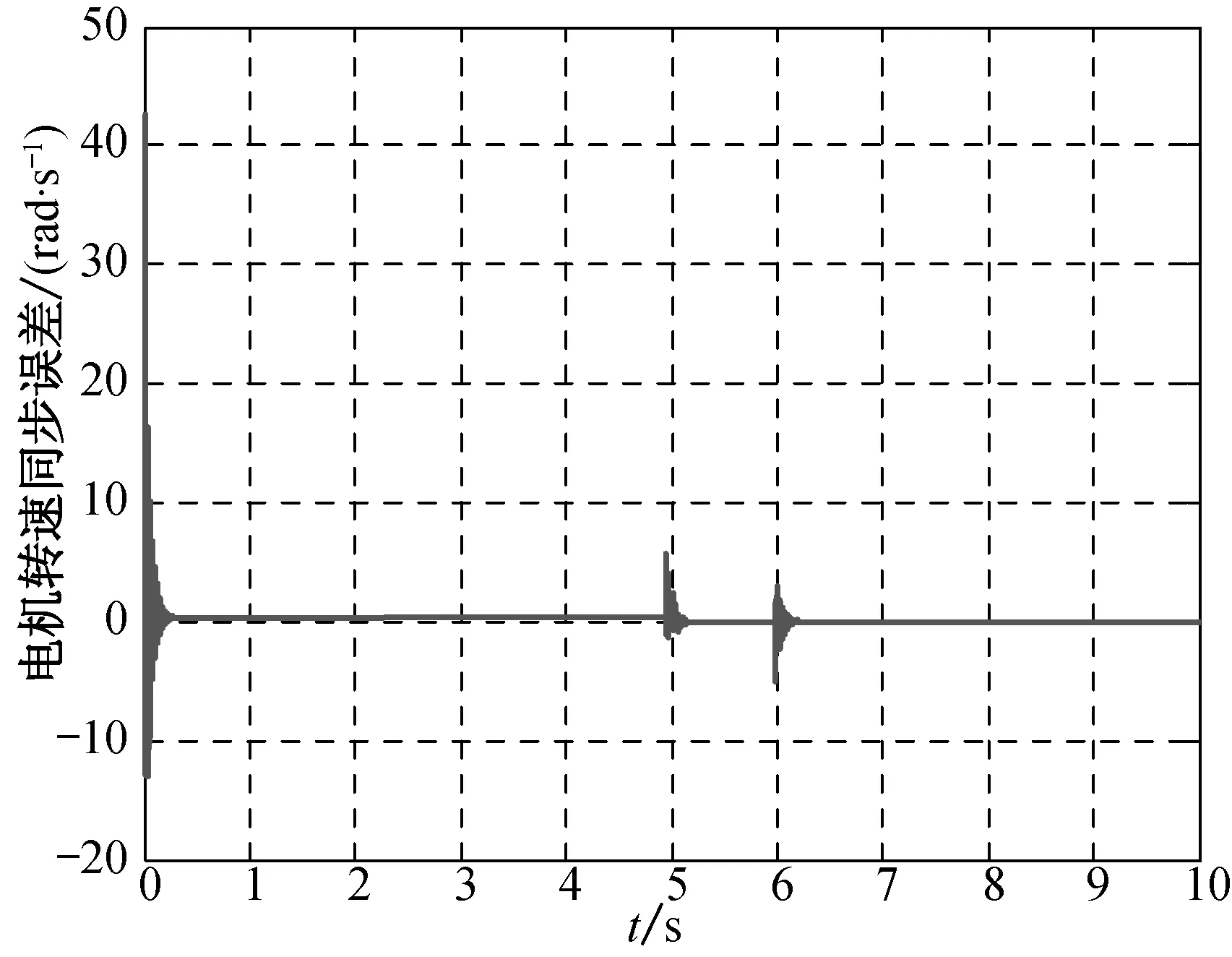
當系統穩定運行之后，分別在5和6 s時給系統添加大小為4 N·m的負載擾動，仿真結果如圖6所示．

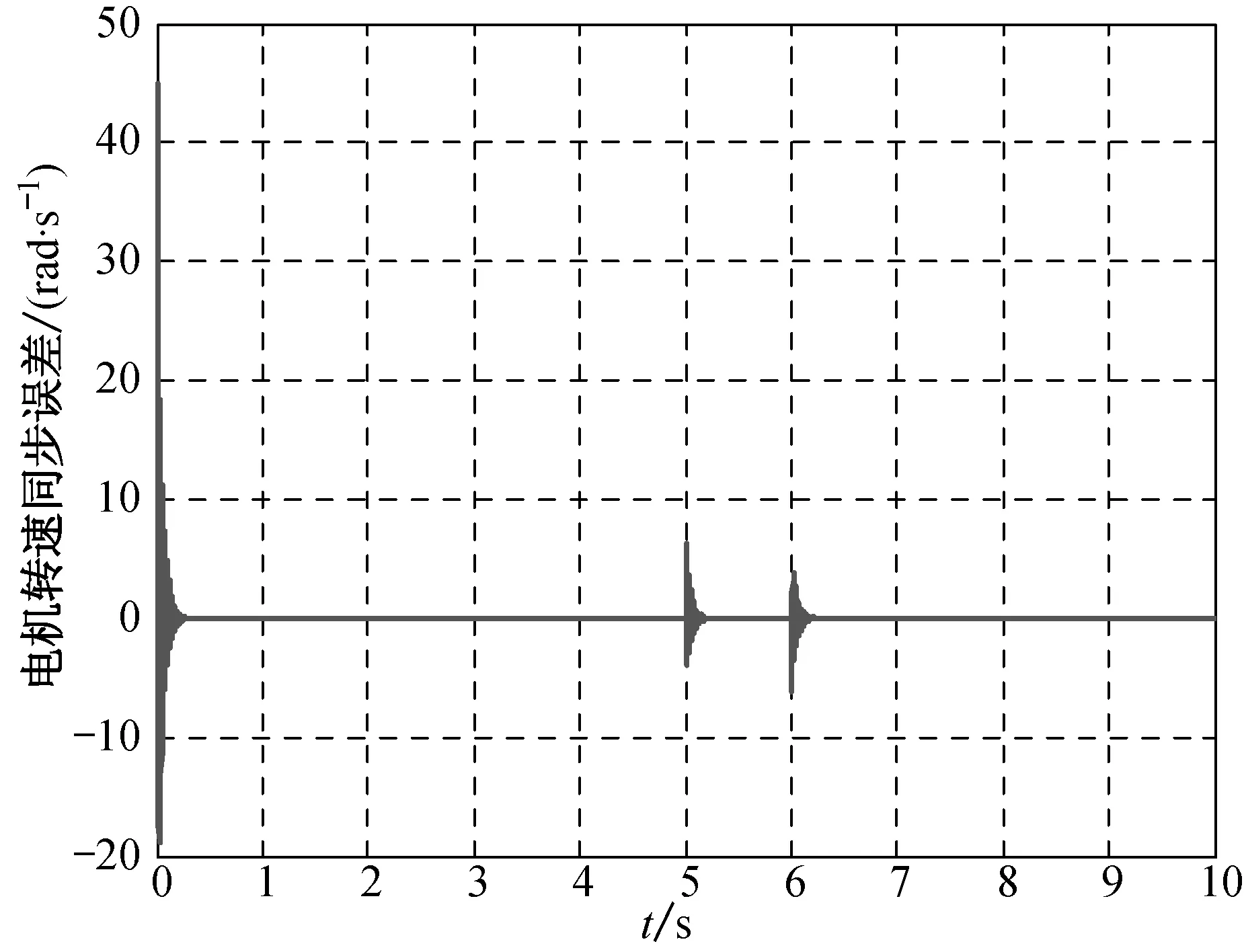
圖6 伺服電機同步誤差Fig．6 Synchronous deviation of the servo-motor

從圖6可以看出，當系統啟動時，外部沒有擾動，電機轉速之間的同步誤差很小，且能快速收斂，系統的同步跟隨性較好．當有擾動產生時，波形變化很小，表明系統具有較好的自適應性和健壯性，同步精度較高，動態性能和同步性能較好．

在控制結構不變的基礎上，同樣是基于搜索和進化思想，采用遺傳算法(GA)優化的PID控制與本文所述的算法進行比較，仿真結果如圖7所示．

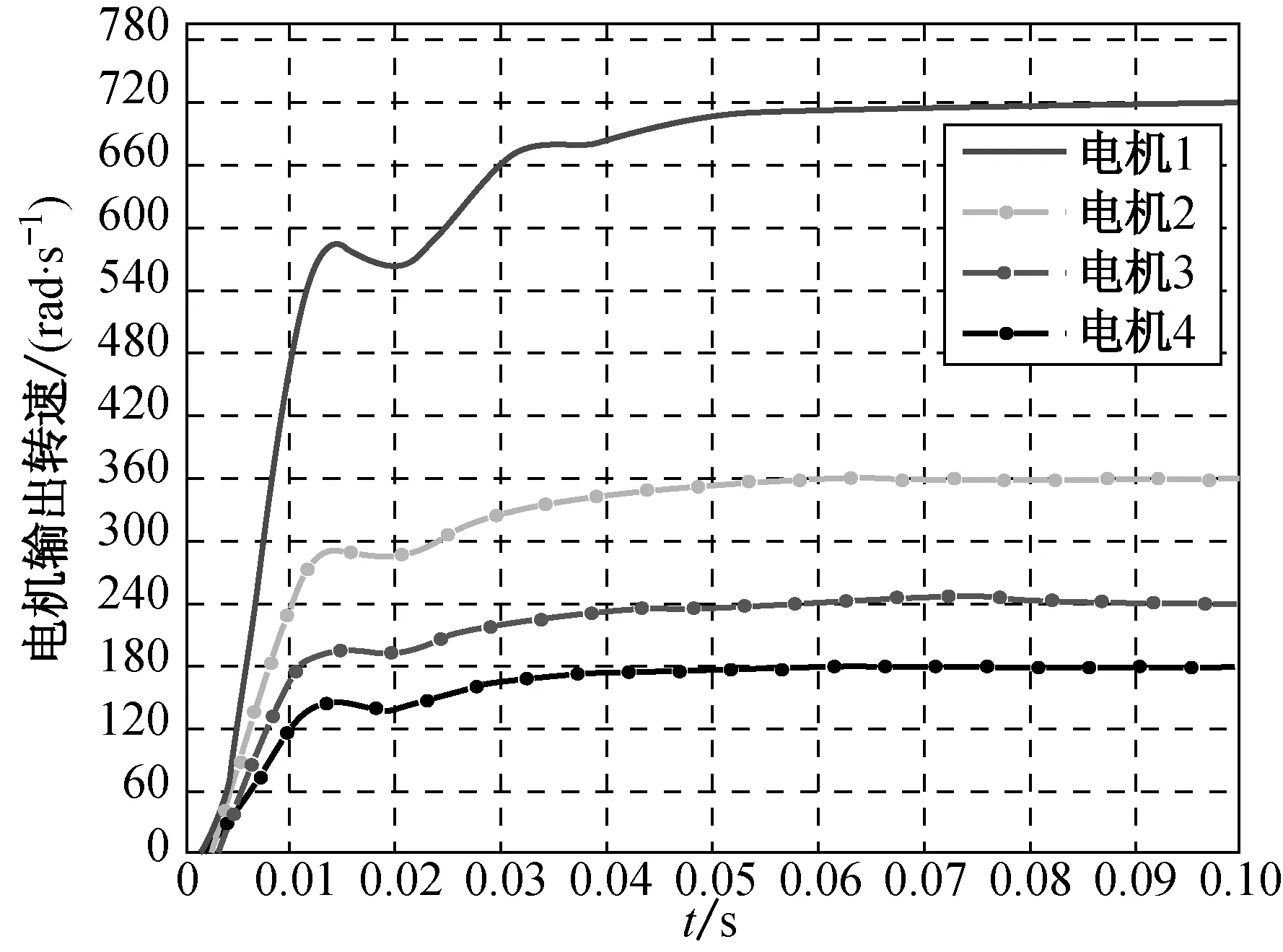
(a) 輸出轉速

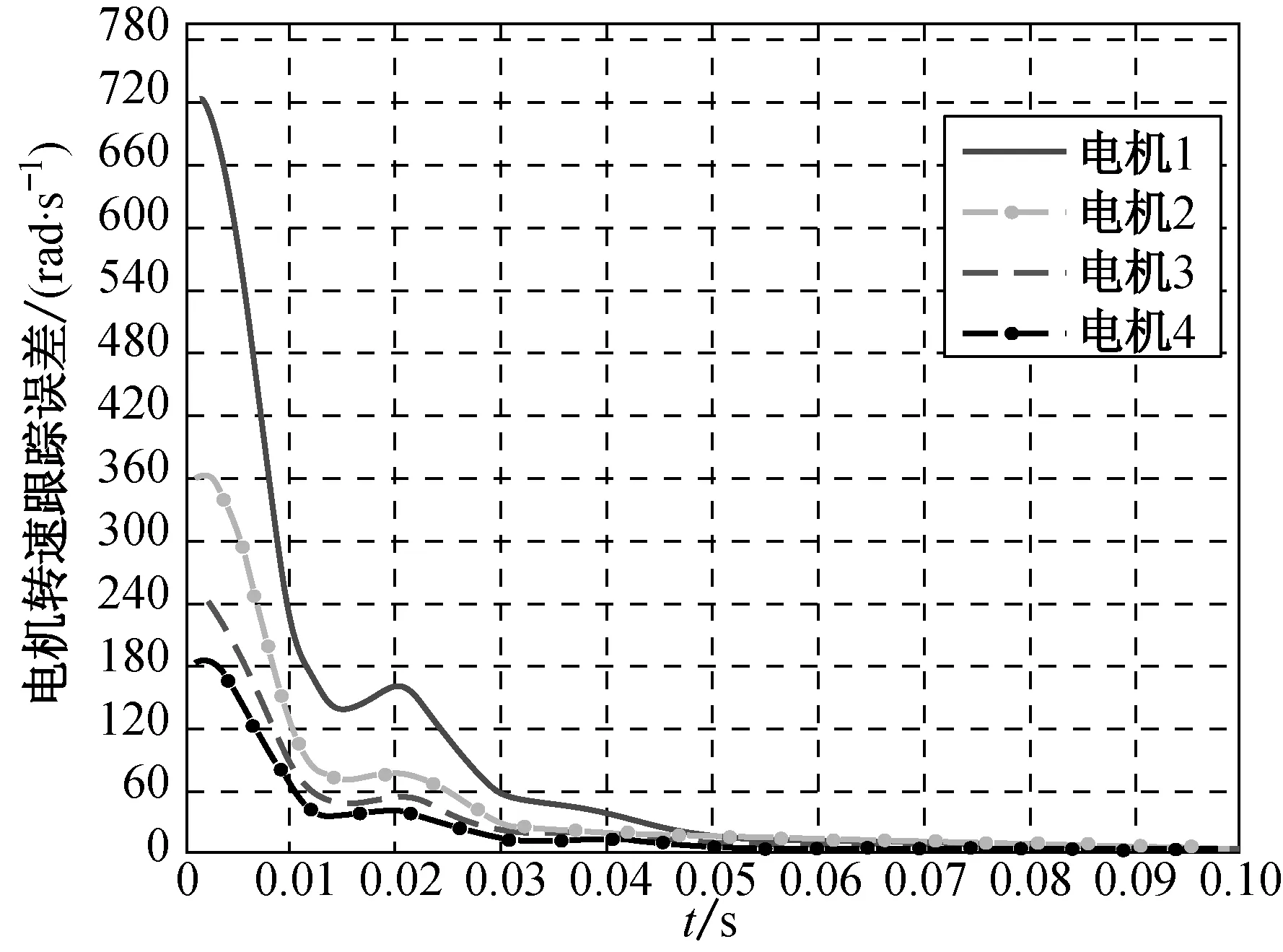
(b) 跟蹤誤差

(c) 同步誤差

從圖6和7(c)的對比可以看出，兩種算法同是基于搜索和進化的思想，同步誤差都很小，體現了智能算法的優越性．但是從電機轉速的跟蹤角度來看，遺傳算法的跟蹤誤差波動較大，收斂速度較為緩慢，收斂時間是SOA算法的2倍，對于高精度、高轉速傳動系統，易出現系統遲滯的現象．

上述仿真試驗表明，本文所述的控制算法在系統從啟動到穩定運行，或者出現負載擾動時，都能穩定快速地收斂誤差，實現電機間的同步運行．這充分表明了基于人群搜索算法的SOA_PID控制在多伺服電機協同控制中有良好的效果，且同步性能和動態性能優于常規的智能控制算法．

4 結 語

本文針對多伺服電機的協同控制問題，利用SOA的搜索和進化能力，將SOA與傳統PID算法相融合，給出了SOA_PID控制器的控制結構和控制算法，并在Matlab/Simulink中對4電機協同控制系統進行了仿真試驗．仿真結果表明，基于SOA的PID控制器能有效提高多伺服電機的同步性能，系統收斂精度高，穩定性能好，收斂速度快，健壯性較好．本文的研究為實現智能算法在多伺服電機高精度、高速度協同的應用上提供了很好的借鑒．

[1] 曹春平，王波，胥小勇，等．基于神經網絡多電機偏差耦合同步控制結構[J]．控制工程，2013，5(3)：415-418．

[2] 王寶仁．PID網絡化運動控制系統多軸協同關鍵技術研究[D]．濟南:山東大學控制科學與工程學院，2008．

[3] 高飛．MATLAB智能算法超級學習手冊[M]．北京：人民郵電出版社，2014．

[4] 劉云平．基于人群搜索算法的PID控制器參數優化[J]．計算機仿真，2014，31(9):347-350．

[5] 胡學同．多電機驅動系統協調控制策略與應用研究[D]．南京:東南大學自動化學院，2004．

[6] 林立，黃蘇融．永磁同步電機系統線性化魯棒控制[J]．電機與控制學報．2009，13(4):541-546．

[7] 程斯一，紀文剛，王志俊．基于模糊PID的多伺服電機交叉耦合同步控制[J]．北京石油化工學院學報，2014，22(4)：54-57．

[8] 苗新剛，汪蘇，韓林攀，等．基于偏差耦合的多電機單神經元同步控制[J]．微電機，2011，44(2)：44-47．

[9] 胡壽松．自動控制原理 [M]．5版．北京：科學出版社．2007：76-121．

[10] 曹玲芝，馬躍軍．基于偏差耦合的PMSM滑模變結構同步控制[J]．微特電機，2012，40(9)：56-58．

[11] 余勝威，曹中清，葛蘆生．新型PID控制及其應用[M]．北京:機械工業出版社，1998．

[12] 劉金琨．先進PID控制MATLAB仿真[M]．北京：電子工業出版社，2011.

[13] XU X Y， SUN Y， FAN H M． Control system of the film casting based on the fieldbus [C]//Proceedings of the 2010 IEEE， International Conference on Mechatronics and Automation. 2010：1320-1324．

[14] CHIU Y C， TOMIZUKA M． Contouring control of machine tool feed drive systems： A task coordinate frame approach[J]. IEEE Transactions on Control Systems Technology， 2001，9(1)：130-139．

[15] YEH S S， HSU P L． Estimation of the contouring error vector for the cross-coupled control design[J]. IEEE/ASME Transactions on Mechatronics， 2002，7(1)：44-51．

[16] SUN D， SHAO X Y， FENG G． A model-free cross-coupled control for position synchronization of multi-axis motions： Theory and experiments[J]. IEEE Transactions on Control Systems Technology， 2007，15(2)：306-314．

[17] SUN D， TONG M C． Asynchronization approach for the minimization of contouring errors of CNC machine tools[J]. IEEE Transactions on Automation Science and Engineering， 2009，6(4)：720-729．

[18] HU C X， YAO B， WANG Q F． Coordinated adaptive robust contouring controller design for an industrial biaxial precision gantry[J]. IEEE/ASME Transactions on Mechatronics， 2010，15(5)：728-735．

[19] YANG J Z， LI Z X． A novel contour error estimation for position loop-based cross-coupled control[J]. IEEE/ASME Transactions on Mechatronics， 2011，16(4)：643-655．

[20] YAO B， HU C X， WANG Q F． An orthogonal global task coordinate frame for contouring control of biaxial systems[J]. IEEE/ASME Transactions on Mechatronics， 2012，17(4)：622-634．

(責任編輯：于冬燕)

Research on Multi-servomotor Synchronous Control Based on Seeker Optimization Algorithm

CHIXinfu，HUANGWenjun，LIPeibo，SUNYize

(College of Mechanical Engineering， Donghua University， Shanghai 201620， China)

Accroding to the multi-servomotor synchronous control system and the multi-servomotor synchronous control system of parameter timevarying， load disturbance and other features， the proportion integration differentiation controller of seeker optimization algorithm with four motors is designed． And the structure of the SOA_PID controller is established by analyzing the principle and characteristics of synchronous control． The simulation platform and the servomotor simulation model are built in Matlab/Simulink． Simulation results show that the SOA_PID controller can effectively improve the multi-servomotor synchronous control performance， the algorithm has a good convergence precision， robust performance and anti-disturbance ability． Compared with conventional PID control， it can achieve the multi-servomotor synchronous control more effectively．

multi-servomotor synchronization； seeker optimization algorithm(SOA)； PID optimization； genetic algorithm

1671-0444(2017)01-0081-07

2015-12-22

國家自然科學基金資助項目(51475091)

郗欣甫(1988—)，男，山東萊蕪人，博士研究生，研究方向為機電系統智能測控技術及多伺服電機協同控制技術.E-mail：chixinfu@yeah.net 孫以澤(聯系人)，男，教授，E-mail：sunyz@dhu.edu.cn

TP 39

A