基于高斯偽譜法的系繩式InSAR系統展開滑模控制

張志剛，張錦繡

(哈爾濱工業大學 衛星技術研究所，黑龍江 哈爾濱，150080)

基于高斯偽譜法的系繩式InSAR系統展開滑模控制

張志剛，張錦繡

(哈爾濱工業大學 衛星技術研究所，黑龍江 哈爾濱，150080)

針對系繩式InSAR系統的快速展開問題，設計一種系繩張力自適應滑模控制器以跟蹤系統展開最優路徑。首先使用系統三維動力學模型，然后面向任務確定系統性能指標和約束，基于高斯偽譜法規劃出系統展開的最優路徑，并且提出一種系繩張力自適應滑模控制器在系統存在模型誤差和外界擾動情況下跟蹤系統最優展開速度，并通過Lyapunov函數證明閉環系統的穩定性。仿真結果表明:在該控制器作用下系統能夠克服模型誤差和外界擾動跟蹤系統最優展開速度，且在最大估計初始偏差情況下展開到目標位置附近，穩態誤差約為1°。

系繩式InSAR系統；最優展開；高斯偽譜法；自適應滑模控制；系繩張力控制

與以TanDEM-X系統[1]為代表的分布式SAR衛星系統干涉基線周期性變化相比，Moccia[2]提出的繩系衛星SAR系統所提供的干涉基線在整個軌道周期內相對穩定，采用單基線即可實現對所有星下點緯度的覆蓋。同時由于采用繩系形式，其在軌展開時間也由前者以天為量級大幅縮短到以小時為量級，大大提高了系統的在軌部署能力，為繩系衛星SAR系統的應急應用提供了可能。

在系繩SAR任務中，系統快速且穩定的成功展開是完成任務的前提。盡管針對空間繩系SAR具體任務的研究相對較少，但已有諸多學者針對普適性繩系衛星系統，尤其是是其展開控制律[3-6]開展了大量研究。Fujii等[7]使用共軛梯度法規劃出繩系衛星系統展開和回收的最優軌跡，并基于Lyapunov函數提出一種反饋控制律來跟蹤最優路徑。Jin等[8]使用擬線性化和截斷Chebyshev級數來規劃3自由度繩系衛星展開最優路徑。文浩等[9]基于二階微分包含將繩系衛星系統非線性時間最優控制問題離散為大規模動態規劃問題。Williams等[10-11]對比了在不同性能指標下繩系衛星系統展開最優路徑。然而由于繩系系統建模時存在不確定性，以及初始狀態偏差和外界擾動均會影響控制效率，因此需要對系統展開進行閉環控制。Williams等[12]將系統在最優軌跡附近線性化，并使用滾動時域法求解線性反饋增益，以使系統能夠克服初始偏差和外界擾動跟蹤最優軌跡，然而該方法計算量較大[13]。

本文針對主星與子星質量近似接近的繩系衛星系統，使用了系統三維動力學模型，然后將系統在Legendre-Gauss-Lobatto配點處離散，結合系統任務設計優化性能指標和約束，將系繩式InSAR系統的快速展開問題轉換為非線性規劃問題。在此基礎上提出一種系繩張力自適應滑模控制器用來抵消模型誤差及外擾擾動，并使用Lyapunov理論證明其穩定性。

1 系繩式InSAR動力學模型

通過系繩連接的繩系衛星系統(見圖1)在圓軌道或小偏心率橢圓軌道運行時會在重力梯度力矩作用下穩定在鉛垂方向或其附近[14]，利用該特性可以將繩系衛星系統作為InSAR系統的搭載平臺來執行對地觀測任務。系統的姿態可以用系繩長度和系繩相對于系統質心軌道坐標系的方位來描述。

由于系繩質量遠小于衛星質量，系統質心可近似認為在衛星質心連線上。另外本文中主星和子星面積比相差不大，故作用在系統上的大氣阻力力矩較小，可作為擾動處理。同時為了簡化系統動力學模型，在建模過程中做出如下假設：將衛星視為質點，認為衛星姿態可控，即不會因為衛星姿態失穩滾轉而導致展開失敗；系統質心軌道為Keplerian軌道；忽略系繩的扭轉和彎曲，則在系統質心軌道坐標系中，其動力學方程可以通過Newton-Eular法推導表示為[12]：

(1)

(2)

(3)

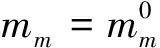
系統質心軌道方程為

(4)

式中:μ為地球引力常數，a為系統質心軌道半長軸。

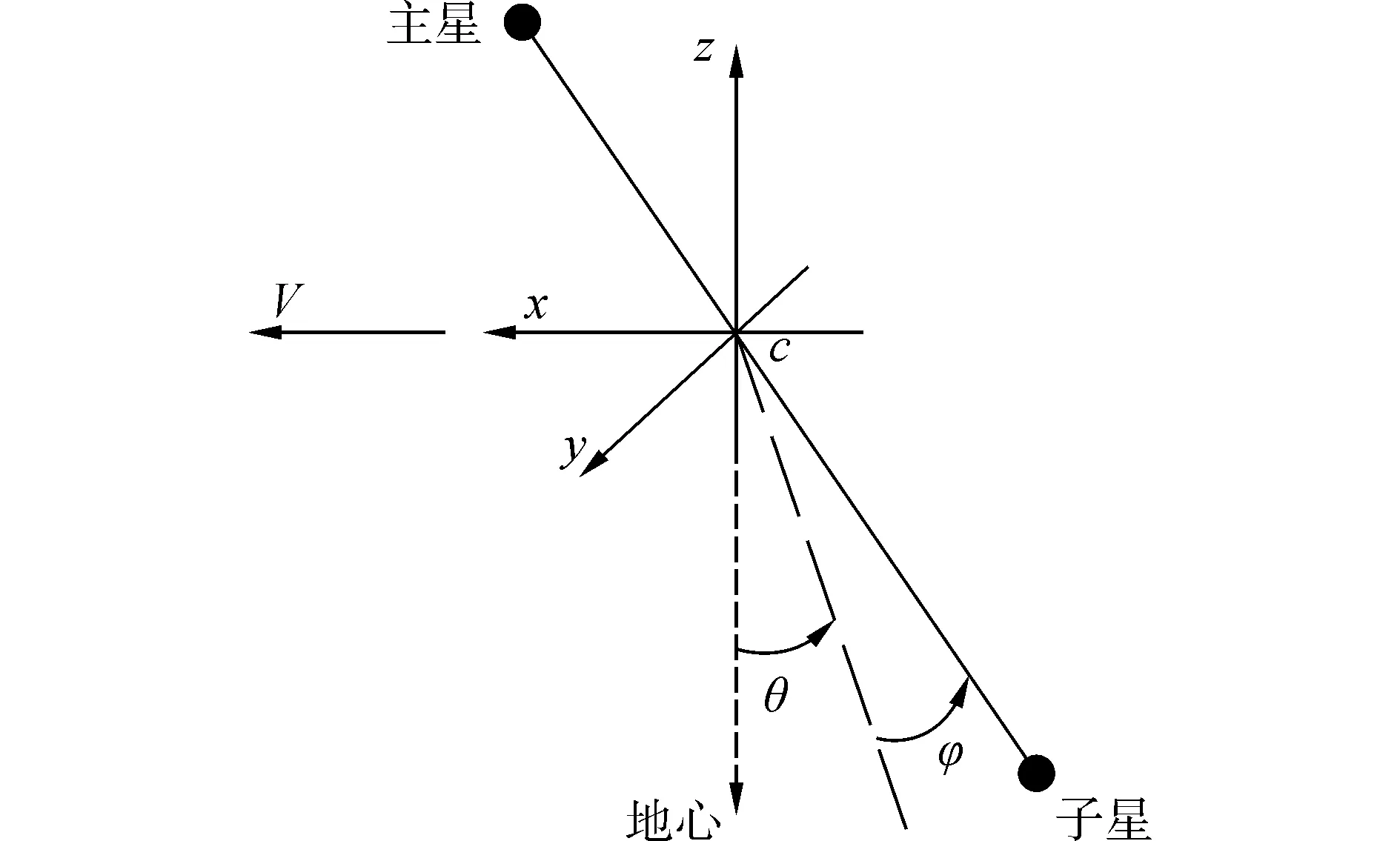
圖1 繩系衛星系統圖Fig.1 The tethered satellite system

2 繩系衛星系統展開最優軌跡規劃

近年來，由于高效的計算效率和對初值的不敏感，偽譜法逐漸成為最優控制問題求解方法的研究熱點[15-18]。而Gauss偽譜法又在近似精度，估計精度及收斂速度上存在優勢，因此選擇Gauss偽譜法來規劃系統展開的最優路徑。

1.1 基于Gauss偽譜法的模型離散

高斯偽譜法將系統的狀態變量和控制變量均進行離散，并通過正交插值多項式對其進行近似。然后通過在配點處將系統狀態變量導數與動力學方程進行比較，從而將動力學方程轉化為約束。將時間區間[t0,tf]轉換到[-1,1]，然后將系統狀態變量和控制變量離散并通過Lagrange插值多項式近似，插值點為

其中LG點不包括初始點和終止點。

系統動力學微分方程寫為

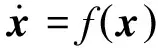
(5)

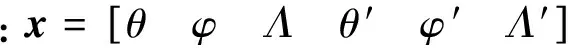
使用高斯偽譜法可以將其在LG點處轉換為動力學約束：

(6)

式中：X(τ)，U(τ)為通過Lagrange插值得到的近似值，具體過程可以參考文獻[16]。

1.2 面向任務的性能指標與約束

以獲取地面DEM數據為目標，工作時的系統基線在cxy平面內，結合繩系衛星系統的穩態構型是沿當地鉛錘方向分布的，因此希望系統能夠展開并穩定在鉛錘方向附近。故系統展開終值應滿足：

(7)

以系繩式InSAR系統快速展開到終端位置為目標，同時使系統控制變量變化平滑，以避免展開過程中產生震蕩。根據上述目標選擇優化性能指標：

(8)

另外系統以系繩張力作為控制變量，因系繩只能產生拉力，故控制變量應始終大于零，又其存在最大值限制。因此控制變量應滿足以下約束：

(9)

最終，結合任務需求系繩式InSAR系統展開最優的性能指標和約束如下：

(10)

本節使用Gauss偽譜法將系統動力學方程離散為約束方程(6)，再選擇合適的性能指標和終端及路徑約束(10)，即將系統展開最優軌跡規劃為題轉化為非線性規劃問題。而對于非線性規劃問題已有多種成熟的優化算法工具包，本文使用序列二次規劃法程序包SNOPT來獲取系統展開的最優軌跡。

3 系繩張力自適應滑模控制器

不考慮模型誤差和外界擾動時，系統展開的偏差主要為插值近似偏差。然而在實際運行過程中，微小外界擾動和初始偏差總是不可避免的，采用開環控制將使系統展過程偏離最優軌跡，導致展開結束后系統存在較大的穩態誤差，情況嚴重時甚至導致展開失敗。因此，設計一種反饋控制器補償系統誤差和外界擾動對于系統展開是必要的。

大量關于繩系衛星系統的研究表明其面內運動與面外運動耦合較弱，通過改變系繩拉力無法有效控制系統的面外擺動[19]。在不考慮外界擾動時，如若系統初始面外擺角和面外擺動角速度為零時，則系統將會一直在軌道平面內運動。在規劃系統展開最優路徑時，設定初始面外擺角和面外擺動角速度均為零，那么得到的系統展開最優軌跡也將一直保持在軌道平面內，因此在設計系統展開反饋控制器時為了方便，僅考慮系統的面內運動，此時φ=φ′=0。另外本文中系繩質量遠小于衛星質量，在設計系統展開反饋控制器時可以忽略系繩質量，此時系統的動力學方程方程(1)～(3)可以簡化為

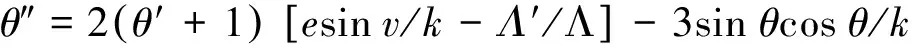
(11)

(12)

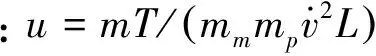
從系統面內運動動力學方程可以發現系統的面內運動受Λ′/Λ控制，若系統能夠跟蹤展開繩長及其展開速度，則存在較小面內初始擺角偏差時，系統能夠展開到目標位置附近。因此希望設計一種系繩張力控制器使系統能夠跟蹤其最優展開速度。

系統展開執行機構輸出與控制指令之間存在誤差，而且為了方便推導，對系統動力學方程(1)～(3)進行了簡化，為了獲取更加準確的結果，此處將上述簡化和誤差以系統模型誤差的方式添加到系統動力學方程(12)中：

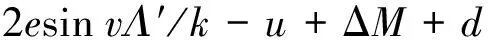
(13)

式中：ΔM為系統建模時由于簡化處理造成的誤差，d為外界擾動。

實際上系統模型誤差和外界擾動均有界，因此可以假設：

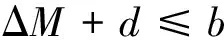
(14)

式中b為一未知非負常數。

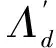
(15)

定義滑模面：

(16)

式中c為正值常數。其相對真近角的一階微分可以表示為

(17)

定理1：系統在系繩張力展開控制律：

(18)

式中:λ、σ>0，控制下能夠跟蹤展開速度的最優軌跡。

證明：

設計Lyapunov函數:

(19)

則其相對真近角的一階微分為

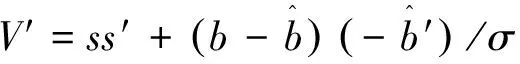
(20)

將式(17)代入式(20)得：

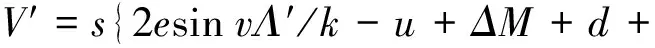
(21)

將式(18)代入可得：

(22)

因此s∈L,∈L，進而得到∈L，進一步得到控制力u∈L，從而s′∈L。使用Barbalat引理可得，進而得到，即系統展開速度能夠跟蹤最優軌跡。

(23)

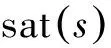
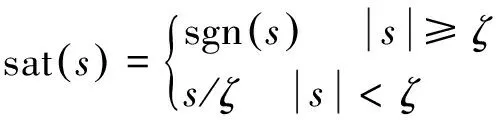
(24)

式中ζ為滑模層厚度。

在控制器(22)作用下的閉環系統能夠跟蹤系統展開最優路徑，其穩定性證明與控制器(18)類似，此處不再累述。相比于以前繩系系統展開控制中所用的反饋控制，控制器(22)能夠克服系統建模中的未知有界誤差和外界擾動，且相比于文獻[12]中的控制方法，減少了控制過程中的計算量，以便于實現實時跟蹤控制。

4 數值仿真分析

根據任務需求選定系統參數：主星質量300kg，子星質量200kg，軌道半長軸6 645km，軌道偏心率0.002 7，系繩長度1km，系繩線密度0.000 185kg/m，系繩彈性模量EA為6 000N。假設初始時刻系統沿鉛錘方向分離，展開機構開始工作時系繩長度為10m，展開速度為2m/s。則無量綱化后系統的初始狀態為

(25)

假設系統展開執行機構滿足下面要求：

0≤T≤5N

由于閉環控制的目標是跟蹤系統展開速度最優軌跡，為了給控制留有裕度，避免系繩回收，設定展開時最小速度為0.05m/s。則系統的展開終端狀態變為

影響系統展開的誤差主要是系統初始狀態偏差和外界攝動影響。其中外界攝動影響在低軌以大氣阻力為主，結合文獻[14]對系統受到的大氣阻力進行估計，在250km軌道高度處1km長的系繩的大氣阻力約為2mN。假定系統使用推力器進行分離，推力器方向偏差最大為5%，且不考慮其對衛星姿態的影響，則系統的初始面內擺角最大約為3°。

為了驗證所設計的控制器效果，分別對系統在開環控制和自適應滑模控制器作用下的展開過程進行仿真。系統所受外界攝動設為fd=2 m·N，模型誤差設為ΔM=0.01sinν1/rad2，其中對外界攝動力做無量綱化處理：

閉環控制仿真參數選擇為

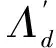
仿真時系統的初始面內擺角偏差變化范圍為±3°，每次變化0.5°。為了節省空間，僅以最大面內偏差Δθ0=3°為例畫圖，其他情況則見表2和表3。

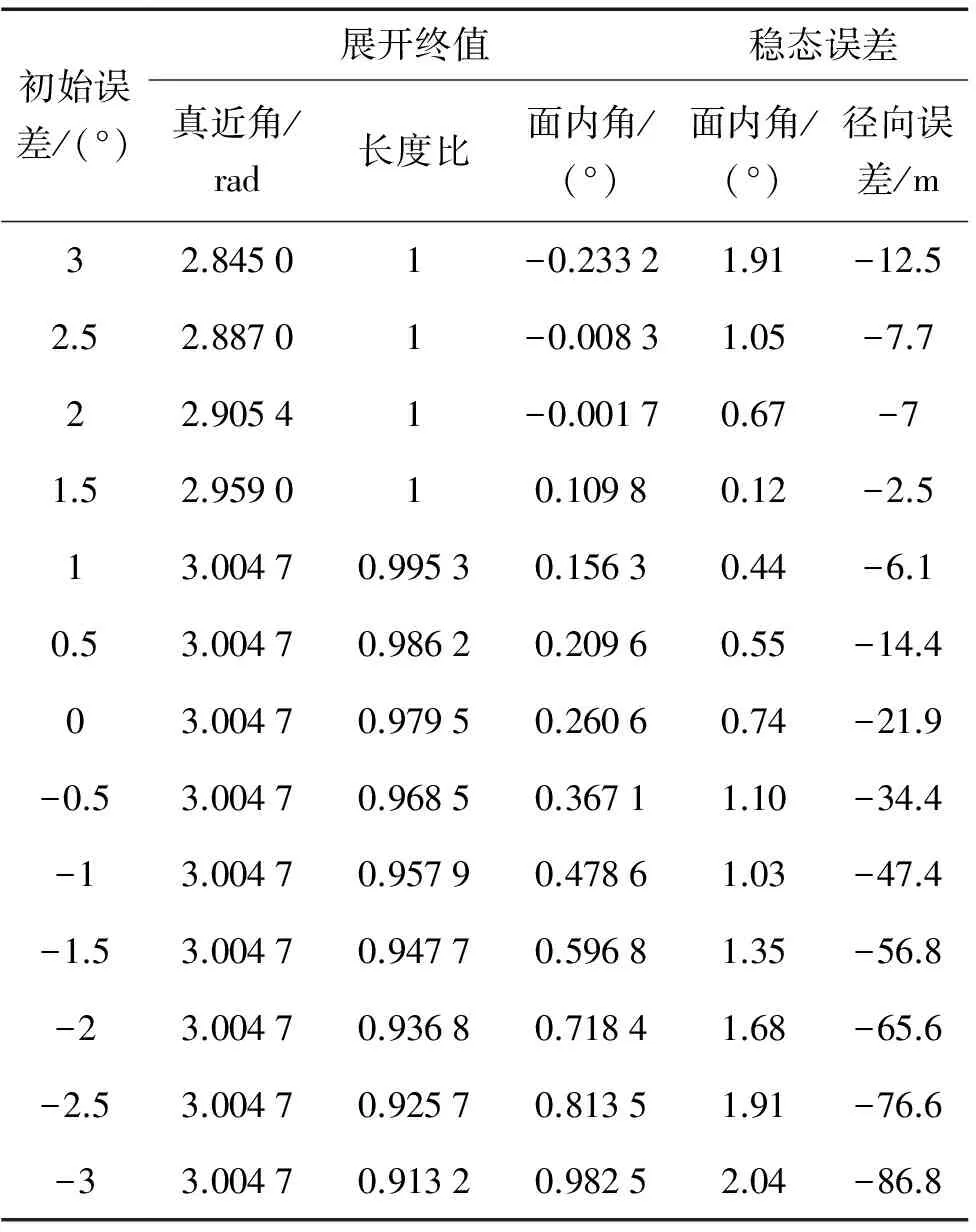
表2 不同初始偏差下的系統開環控制展開及穩態誤差

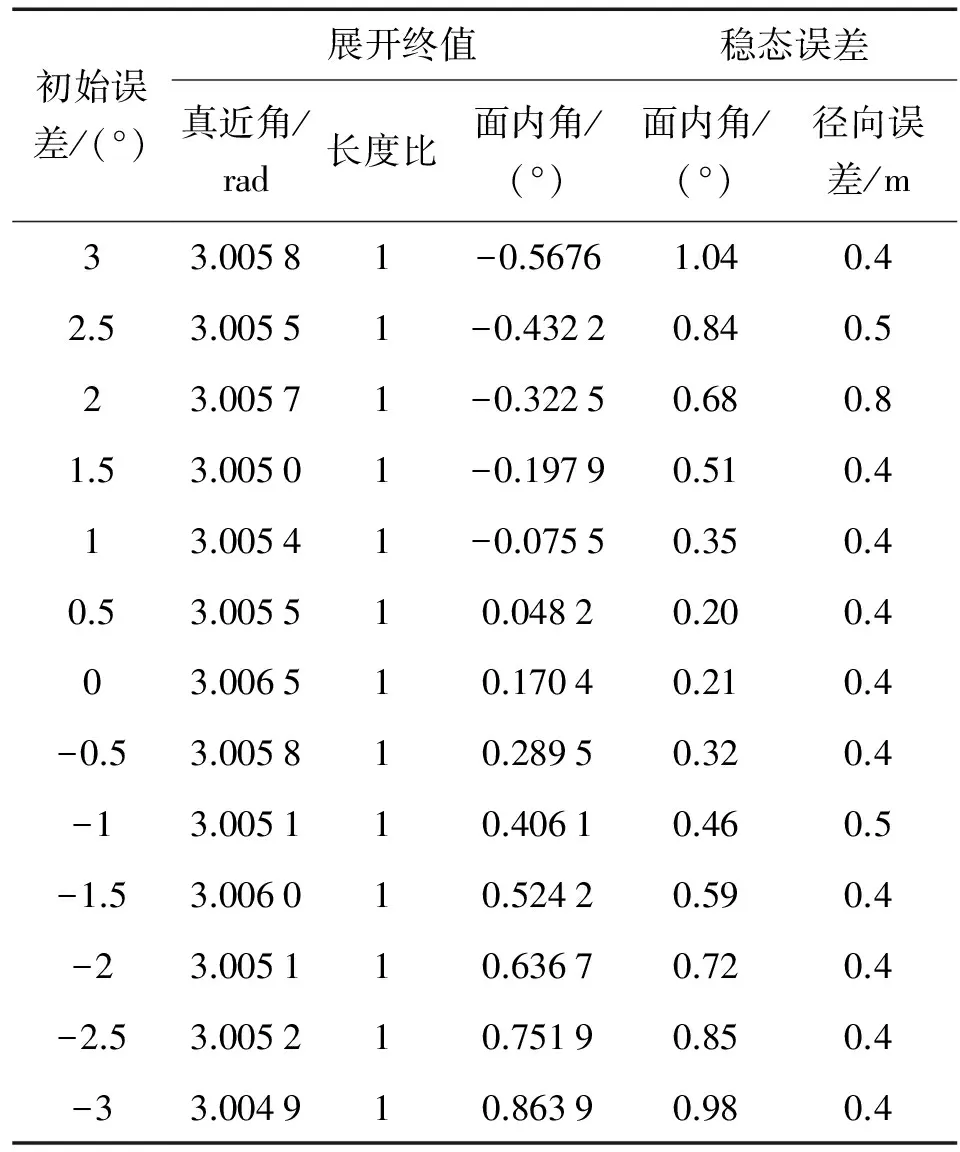
表3 不同初始偏差下的系統閉環控制展開及穩態誤差

由仿真圖2～5可知，當系統面內擺角初始偏差為3度時，系統在開環控制下和閉環控制均能展開到目標長度，且系統面外運動不受面內運動影響。由圖2知在兩種控制下系統的面內擺角均在最優軌跡附近，但是開環控制的穩態誤差約為閉環控制的2倍。系統的面內角速度亦如此。由于假設系統的面外擺角不存在初始偏差，系統的面內擺角偏差不影響面外運動，這也驗證了二者的耦合較弱。

圖4和5為系統沿系繩徑向的變化。圖4顯示閉環控制能夠有效減弱系統穩態階段的徑向震蕩。可見兩種控制均能在半個軌道周期內將系統展開，且開環控制更快一些。而閉環控制下，穩態階段兩顆衛星距離變化范圍遠小于開環控制，且相對速度亦比開環控制小幾倍。

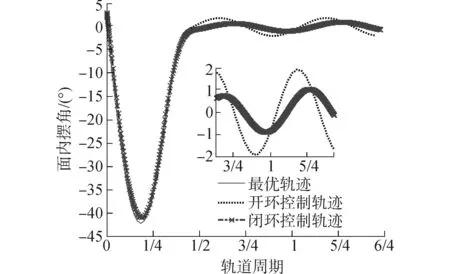
圖2 開環與閉環控制下系統面內擺角變化Fig.2 The in-plane angle variations under two control laws and optimal trajectory

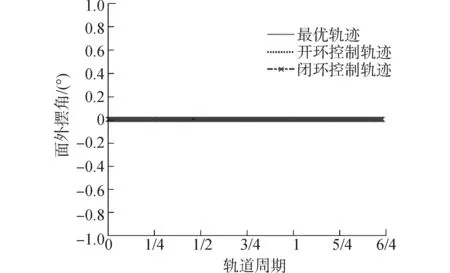
圖3 開環與閉環控制下系統面外擺角變化Fig.3 The out-plane angle variations under two control laws and optimal trajectory

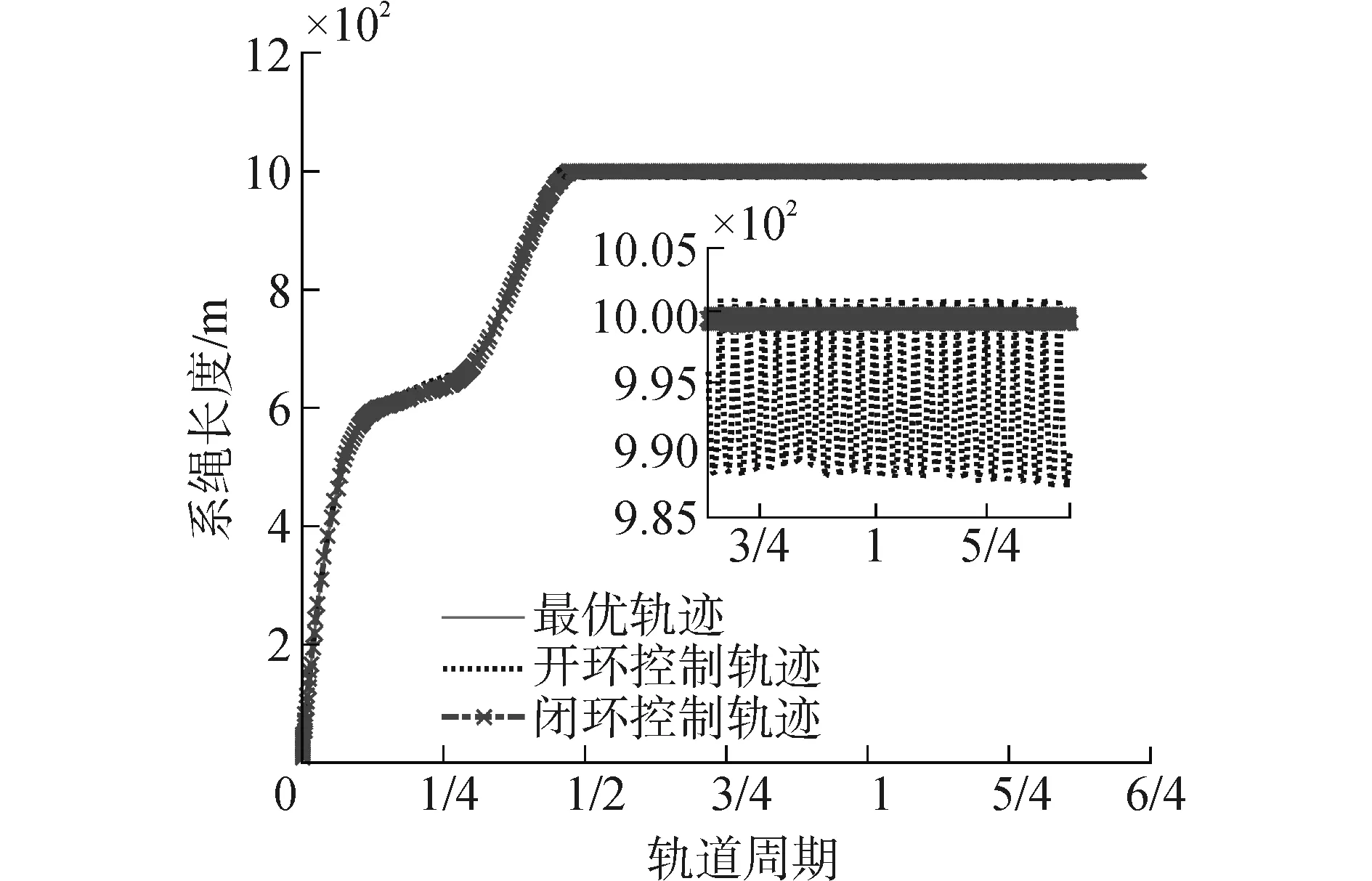
圖4 開環與閉環控制下系繩長度變化Fig.4 The tether length variations under two control laws and optimal trajectory

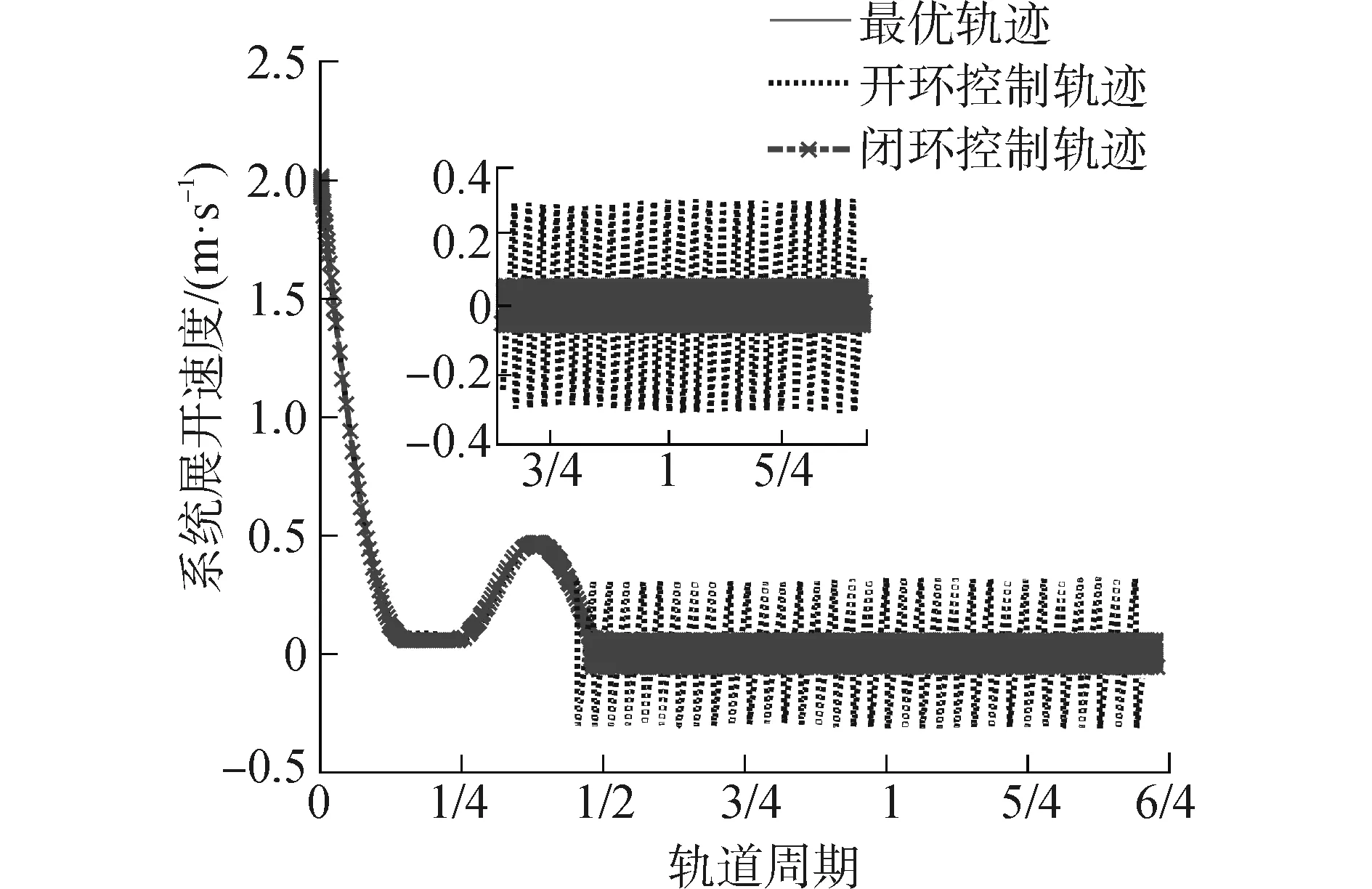
圖5 開環與閉環控制下系繩徑向變化速度Fig.5 The deploy velocities under two control laws and optimal trajectory

圖6所示，閉環控制時系統控制力相對開環控制力僅有微小增幅，而系統的穩態誤差相對開環控制明顯減小，因此該控制律是相當有效的。

圖7為系統在兩種控制下的面內運動軌跡及最優軌跡，表明閉環控制下系統穩態誤差更小，這也與系統在閉環控制下有著更小的面內擺角誤差和徑向誤差相對應。

從系統面內運動軌跡來看系統展開結束后存在穩態誤差，其原因一方面是由于展開跟蹤控制器的抖動影響，導致系繩展開完成后速度不完全為零，如果選擇較小的邊界層厚度ζ，系繩展開結束速度會更小，但變化頻率會更快；另一方面如文獻[14]中指出當系統軌道為橢圓時，系統運行過程中系繩不會保持鉛垂方向分布，即系繩的面內擺角不會一直保持為零，由系統動力學方程方程(1)～(3)可知系統面內運動存在強耦合，這也會導致系統展開后系繩長度和變化速度的震蕩。不過，可以通過阻尼器來減弱系統運行過程中的縱向震蕩。

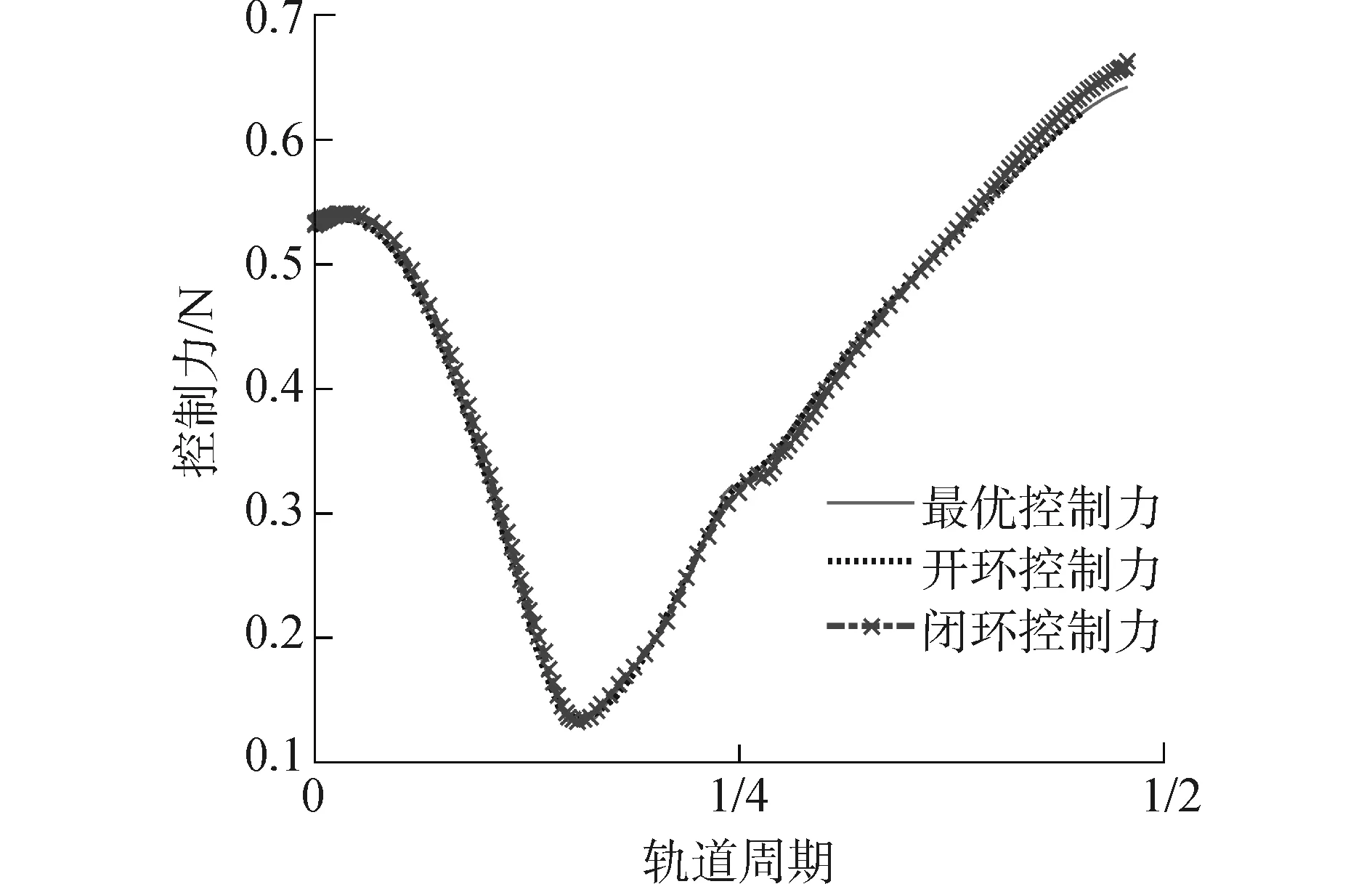
圖6 開環與閉環控制下系統控制力Fig.6 The control forces under two control laws and optimal trajectory

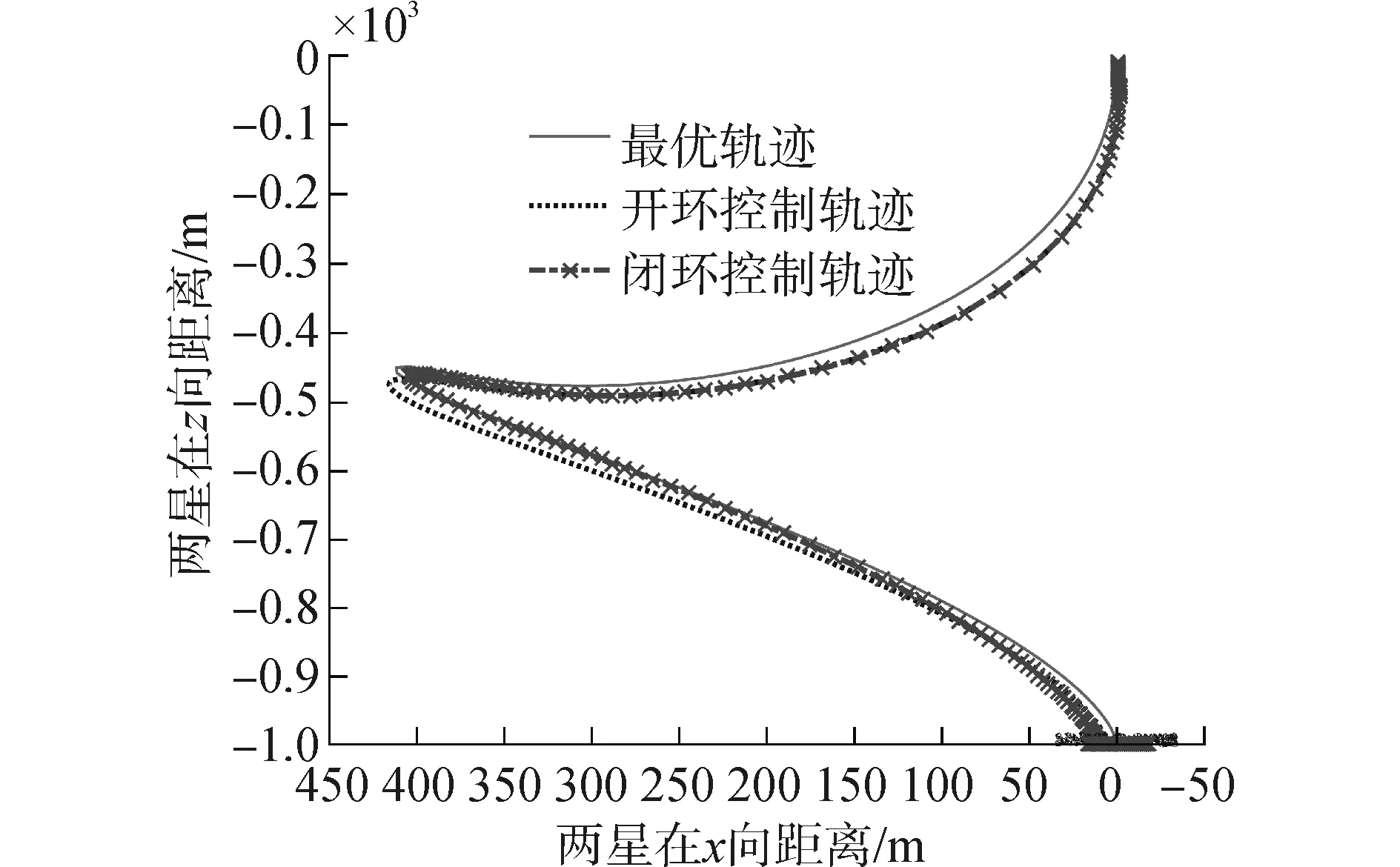
圖7 開環與閉環控制下系統面內運動軌跡Fig.7 The in-plane trajectories under two control laws and optimal trajectory

為了驗證該控制器的適用性，對不同面內擺角初始偏差下的系統分別進行開環控制和閉環控制，系統展開時間，展開長度和穩態階段誤差分別見表2和表3。

從表2的結果可以知道，不同初始面內擺角偏差對開環控制影像很大。隨著面內初始擺角偏差的減小，系統展開時間增加，當面內初始偏差減到1°時，系統在閉環控制下已無法在規定時間內完成展開，且系統展開長度會隨著面內擺角初始偏差的反向增大而減小。當面內初始擺角偏差為1.5°時，系統的穩態誤差最小，而理論上當面內初始擺角偏差為0時系統穩態誤差最小，這是因為在開環控制下系統穩態誤差除了受到面內初始擺角偏差的影響外，還受到外界擾動和建模誤差的影響。當系統為開環控制時，有意使系統初始面內擺角偏差為正值有利于系統的展開，且若選擇合適也可使系統展開到目標位置附近。

從表3可以知道，系統在閉環控制下均能夠展開到目標位置附近，不過展開時間稍有偏差。相比開環控制，系統的穩態誤差明顯減小，特別是系繩徑向穩態誤差，最大為0.8m，繩長變化速率最大為0.08m/s。系統面內擺角誤差則隨著初始誤差的減小而減小，但由于外界擾動的存在，當面內擺角初始誤差為零時其穩態誤差并不為零。雖然系統在開環控制下也有幾率展開的目標位置附近，但是亦有很大幾率在規劃時間內無法完成展開。因此相比于開環控制，所設計的系繩張力自適應滑模控制器能夠保證系統在規劃時間內展開到目標位置附近，快速完成系統配置。

4 結論

本文面向系繩式InSAR系統任務要求，基于高斯偽譜法規劃出系統快速展開的最優軌跡，并通過反饋控制使系統展開跟蹤最優軌跡，結論如下：

1)所設計的系繩張力自適應滑模控制器可以克服系統模型誤差和外界擾動跟蹤系統最優展開軌跡；

2)在閉環控制下系統能夠展開到目標位置附近，且系統面內擺角穩態誤差隨著系統面內擺角初始誤差的減小而減小；

3)與開環控制相比，閉環極大地提高了系統展開的成功率，有效地降低了系統的穩態誤差，使系統能夠完成快速配置。

[1]KRIEGER G, MOREIRA A, FIEDLER H, et al. TanDEM-X: a satellite formation for high-resolution SAR interferometry[J]. IEEE transactions on geoscience and remote sensing, 2007, 45(11): 3317-3341.

[2]MOCCIA A, VETRELLA S. A tethered interferometric synthetic aperture radar (SAR) for a topographic mission[J]. IEEE transactions on geoscience and remote sensing, 1992, 30(1): 103-109.

[3]CHEN Yi, HUANG Rui, HE Liping, et al. Dynamical modelling and control of space tethers: a review of space tether research[J]. Nonlinear dynamics, 2014, 77(4): 1077-1099.

[4]KRUPA M, POTH W, SCHAGERL M, et al. Modelling, dynamics and control of tethered satellite systems[J]. Nonlinear dynamics, 2006, 43(1/2): 73-96.

[5]SUN Guanghui, ZHU Z H. Fractional-order tension control law for deployment of space tether system[J]. Journal of guidance, control, and dynamics, 2014, 37(6): 2057-2062.

[6]MISRA A K. Dynamics and control of tethered satellite systems[J]. Acta astronautica, 2008, 63(11/12): 1169-1177.

[7]FUJII H A, ANAZAWA S. Deployment/retrieval control of tethered subsatellite through an optimal path[J]. Journal of guidance, control, and dynamics, 1994, 17(6): 1292-1298.

[8]JIN D P, HU H Y. Optimal control of a tethered subsatellite of three degrees of freedom[J]. Nonlinear dynamics, 2006, 46(1/2): 161-178.

[9]文浩, 金棟平, 胡海巖. 基于微分包含的繩系衛星時間最優釋放控制[J]. 力學學報, 2008, 40(1): 135-140. WEN Hao, JIN Dongping, HU Haiyan. Time-optimal deployment of a tethered subsatellite based on differential inclusion[J]. Chinese journal of theoretical and applied mechanics, 2008, 40(1): 135-140.

[10]WILLIAMS P. Optimal deployment/retrieval of tethered satellites[J]. Journal of spacecraft and rockets, 2008, 45(2): 324-343.

[11]WILLIAMS P. Optimal deployment/retrieval of a tethered formation spinning in the orbital plane[J]. Journal of spacecraft and rockets, 2006, 43(3): 638-650.

[12]WILLIAMS P, HYSLOP A, STELZER M, et al. YES2 optimal trajectories in presence of eccentricity and aerodynamic drag[J]. Acta astronautica, 2009, 64(7/8): 745-769.

[13]PENG Haijun, GAO Qiang, WU Zhigang, et al. Efficient sparse approach for solving receding-horizon control problems[J]. Journal of guidance, control, and dynamics, 2013, 36(6): 1864-1872.

[14]ALPATOV A P, BELETSKY V V, DRANOVSKII V I, et al. Dynamics of tethered space systems[M]. London: CRC Press, 2010: 20-50.

[15]雍恩米, 陳磊, 唐國金. 飛行器軌跡優化數值方法綜述[J]. 宇航學報, 2008, 29(2): 397-406. YONG Enmi, CHEN Lei, TANG Guojin. A survey of numerical methods for trajectory optimization of spacecraft[J]. Journal of astronautics, 2008, 29(2): 397-406.

[16]黃詰, 張友安, 王麗英, 基于Radau偽譜法的非線性最優控制問題的收斂性[J]. 控制理論與應用, 2014, 31(2): 263-267. HUANG Jie, Zhang You′an, WANG Liying. Convergence of nonlinear optimal control problem using Radau pseudospectral method[J]. Control theory & applications, 2014, 31(2): 263-267.

[17]徐少兵, 李升波, 成波. 最優控制問題的Legendre偽譜法求解及其應用[J]. 控制與決策, 2014, 29(12): 2113-2120. XU Shaobing, LI Shengbo, CHENG Bo. Theory and application of Legendre pseudo-spectral method for solving optimal control problem[J]. Control and decision, 2014, 29(12): 2113-2120.

[18]閆循良, 廖守億, 張金生, 等. 基于節點改善策略的偽譜軌跡優化[J]. 宇航學報, 2013, 34(7): 891-900. YAN Xunliang, LIAO Shouyi, ZHANG Jinsheng, et al. Trajectory optimization using pseudospectral method based on a grid node refinement strategy[J]. Journal of astronautics, 2013, 34(7): 891-900.

[19]FEDI CASAS M. Dynamics and control of tethered satellite formations in low-earth orbits[D]. Barcelona: Universitat Politècnica de Catalunya, 2015: 18-50.

Sliding mode control of a tethered InSAR system deployment on the basis of the Gauss pseudospectral method

ZHANG Jinxiu，ZHANG Zhigang

(Research Center of Satellite Technology, Harbin Institute of Technology, Harbin 150080, China)

The rapid deployment of a tethered InSAR was studied in the study. The Gauss pseudospectral method (GPM) was used to plan the optimal deployment trajectory and an adaptive sliding mode controller was proposed to counteract the adverse impact of modeling error and external disturbances. First, a simple system model was used and discretized as constraints by GPM. Second, the optimal deployment trajectory that can satisfy the mission requirement was acquired. Finally, an adaptive sliding mode controller was designed to track the optimal deployment velocity trajectory and stability was analyzed using Barbalat′s lemma. Numerical simulations show the system could deploy in the vicinity of the target location under the controller with a maximum steady error of 1 degree.

tethered InSAR system; optimal deployment; Gauss pseudospectral method; adaptive sliding mode control; tension control

2015-09-17.

日期：2016-11-14.

國家自然科學基金重大計劃項目(91438202).

張志剛(1988-), 男, 博士研究生； 張錦繡(1978-), 男, 教授,博士生導師.

張志剛，E-mail:zhzhghit@126.com.

10.11990/jheu.201509055

http://www.cnki.net/kcms/detail/23.1390.u.20161114.1036.026.html

V448.22

A

1006-7043(2017)02-0293-07

張志剛，張錦繡. 基于高斯偽譜法的系繩式InSAR系統展開滑模控制[J]. 哈爾濱工程大學學報， 2017, 38(2): 293-299. ZHANG Jinxiu，ZHANG Zhigang. Sliding mode control of a tethered InSAR system deploymenton the basis of the Gauss pseudospectral method[J]. Journal of Harbin Engineering University, 2017, 38(2): 293-299.