三種柔性蒙皮支撐結構的力學特性*

沈 元， 朱 華， 劉衛東， 昂海松

(1.南京航空航天大學飛行器結構力學與控制教育部重點實驗室 南京，210016)(2.南京航空航天大學機械結構力學及控制國家重點實驗室 南京，210016)(3.河海大學能源與電氣學院 南京，211100)

三種柔性蒙皮支撐結構的力學特性*

沈 元1， 朱 華2， 劉衛東3， 昂海松2

(1.南京航空航天大學飛行器結構力學與控制教育部重點實驗室 南京，210016)(2.南京航空航天大學機械結構力學及控制國家重點實驗室 南京，210016)(3.河海大學能源與電氣學院 南京，211100)

理論推導了U型、V型和梯形3種柔性蒙皮支撐結構面內橫向無量綱化彈性模量與其平面幾何參數(壁厚系數t、高度系數h、形狀系數k)之間的關系：其等效彈性模量隨t增大而增大，隨h增大而減小，隨k增大而減小。采用ANSYS軟件進行了有限元模擬并通過實驗對其面內力學特性進行驗證。同樣參數條件下，3種結構面內橫向剛度從大到小依次為V型、U型和梯形。說明梯形結構具有更強的變形能力，產生同樣的變形需要的能量最小。對3種結構的面法向剛度進行了有限元仿真和實驗比較，其面法向剛度隨幾何參數的變化規律與面內等效彈性模量相似；在相同等效面法向氣動載荷作用下, 3種結構面法向位移大小依次為梯形、U型和V型。對3種結構拉伸前后不同載荷作用下的面法向最大位移進行實驗測量，發現面法向剛度在拉伸后都有較大提升，在產生相同的面法向位移情況下，承受的壓強平均提高了30%～60%。

變形機翼； 柔性蒙皮； 蜂窩結構； 彈性模量； 有限元分析； 面內拉伸； 法向變形

引 言

傳統飛行器通常針對某種特定的飛行狀態進行設計，在該飛行狀態下能表現出較好的性能，而在其他飛行狀態下性能則有所下降。隨著飛行器設計研究經驗的不斷積累和其他學科技術的進步，為克服傳統飛行器這種單任務模式的缺點，科學家們提出了變體飛行器的概念。變體飛機是指能夠在飛行中改變氣動外形,使飛機在不同飛行狀態下性能保持最佳的飛行器[1]。機翼是飛機升力和操縱力的主要來源，是飛機設計的首要研究對象。相對于傳統機翼，變形機翼能替代傳統的鉸鏈舵面，保證其氣動外形的完整性，大大提高其氣動性能。變形機翼要在飛行過程中進行變形，離不開柔性蒙皮[2-3]、變形作動器[4]及變形機構[5-8]等關鍵技術的支持。柔性蒙皮主要用于在變形時承受并傳遞氣動載荷，保證機翼表面光滑，使機翼具有良好的氣密性。

傳統的固定翼或者剛性變體飛機采用的蒙皮都是剛性金屬蒙皮，通常采用鋁合金材料加工制造。在柔性變形機翼中，傳統的蒙皮由于面內剛度太大，無法跟隨機翼結構變形而變形。針對傳統蒙皮的不足，科學家們已經提出了多種柔性蒙皮支撐結構，并對采用柔性材料制造的蒙皮樣本進行了深入研究[9-11]。但是，由于材料性能的限制和變形機翼對柔性蒙皮的高要求，現有的蒙皮支撐結構還存在面內柔性與面法向剛性不足和制造工藝復雜等缺陷[12-14]，因此需要對蒙皮支撐結構進行深入設計與優化，開發出滿足力學性能要求且易于加工制造的柔性蒙皮和相應的支撐結構。

蜂窩夾心結構具有結構輕、承載能力強和加工工藝成熟的特點，在飛機上越來越多地得到應用，因此采用蜂窩結構來支撐柔性蒙皮具有很高的可行性。國內外學者對此做了大量研究。文獻[15-16]對零泊松比的六邊形蜂窩和V型柔性蒙皮支撐結構的面內力學特性進行了研究，發現其面內剛度只有原始制備材料的0.1%～10%，并證明了柔性蒙皮在非變形方向被約束時，這兩種結構的面內橫向無量綱化等效彈性模量(結構的彈性模量與制備材料彈性模量的比值)均不會增加。 Bubert等[17]設計并制造了一種基于V型支撐結構的一維被動變形的柔性蒙皮，發現其在滿足大變形條件下具有較好的承載能力。魯超等[18]對V型零泊松比蜂窩芯斜壁板大變形條件下的彎曲變形和蜂窩芯橫壁板小變形條件下的變形進行分析，證明其大變形方向上的等效彈性模量具有明顯的非線性特征。這些研究僅僅是針對某種平面構型的蜂窩支撐結構進行分析，對不同構型支撐結構的面內和面法向特性缺乏系統性的比較，無法在實際應用中對結構的選用給出明確指導。

筆者選取3種不同構型的柔性蒙皮支撐結構作為研究對象：V型、U型和梯形。采用能量法對3種結構的橫向無量綱化等效彈性模量理論模型進行了推導，并通過數值仿真與實驗研究對該理論模型進行驗證，最后利用數值仿真和實驗研究對3種結構的面法向剛度進行探討。

1 三種構型蜂窩支撐結構面內伸縮特性分析

1.1 理論模型推導

圖1為不同構型柔性蒙皮支撐結構的平面示意圖。圖2為各構型蜂窩單元的參數定義和受力情況。每個單元長度為l，高度系數為h(即高度為hl)，壁厚系數為t(即壁厚為tl)，單元法向厚度為b，其中梯形結構單元形狀參數比其他結構多一個即形狀系數k。下面以V型結構為例對其進行力學分析。考慮到結構和載荷的對稱性，取V型蜂窩的半單元結構進行研究，圖3為V型結構的半單元結構示意圖。點a固定，受拉力Fa和彎矩Ma作用；點b在拉力Fb和彎矩Mb作用下平移至點b′。為求取單元x方向的彈性模量，需要求得點b在x方向的位移δx。

根據圖3，對V型結構半單元分段求解,由x方向平衡可得

Fa=Fb=Fc=Fx

(1)

假設Fa=Fb=Fc=Fx=F，根據力和力矩的平衡，從圖4可以得出

M(x)+Ma=2Fhx

(2)

截面轉角與彎矩的關系為

(3)

其中

(4)

轉角邊界條件為

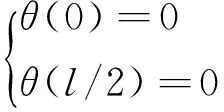
(5)

圖1 3種構型柔性蒙皮支撐結構平面圖Fig.1 Schematic plan of the three structures

圖2 不同構型蜂窩單元面內受力示意圖Fig.2 In-plane force analysis of the celluar unit of the three structures

圖3 V型結構的半單元結構受力示意圖Fig.3 In-plane force analysis of half a unit of the V-type cellular

圖4 V型結構的半單元0-x段結構受力分解Fig.4 Force decomposition of 0-x segment of half a unit of the V-type cellular

聯立式(2)～(5)，求解得到

(6)

《F》狀態內力彎矩為

(7)

《1》狀態內力彎矩為

(8)

《F》狀態軸力為

(9)

《1》狀態軸力為

(10)

根據能量法有

(11)

將式(7)～(10)代入式(11)，積分得到

(12)

V型蜂窩支撐結構的面內橫向等效應力和等效應變為

(13)

V型蜂窩支撐結構的面內橫向無量綱化等效彈性模量為

(14)

其中：E為原材料的橫向彈性模量。

采用同樣方法可推導出U型結構的面內無量綱化等效彈性模量為

(15)

梯形結構的面內橫向無量綱化等效彈性模量為

(16)

其中：k為形狀系數，梯形結構需要3個參數描述。

1.2 基于ANSYS的有限元分析

利用ANSYS的參數化設計語言(ansysparametric design language，簡稱APDL)建立3種結構的參數化有限元模型，如圖5所示。采用Solid45單元劃分網格，彈性系數取為E=1.7 GPa(與實驗采用的材料一致)，泊松比設為0.3。根據單元結構對稱性采用半單元計算，半單元左端面固支，右端面施加位移載荷，通過有限元仿真得到半單元結構左端面的橫向支反力，求得結構的面內橫向無量綱化等效彈性模量。為方便與實驗比較，有限元模型中統一取l=30 mm，法向厚度b=3 mm。對參數h，t和k等取多種組合進行計算，得到結構的面內橫向無量綱化等效彈性模量與結構形狀參數的關系。

圖5 3種結構ANSYS半單元有限元模型Fig.5 FEM model of half a unit of the three structures in ANSYS

1.3 面內拉伸實驗

實驗材料選用厚度b=3 mm的POM板(聚甲醛板)，選取不同的形狀參數進行組合(單元長度l均取30 mm)，對板材進行雕刻加工，得到所需的實驗試件。力-位移測試設備采用微機控制電子萬能試驗機。圖6為結構試件的加載實驗示意圖。

圖6 V型、U型和梯形結構試件加載實驗Fig.6 Loading experiment of the three types of the cellular structures

試件采用4×4的單元分布，固支邊并列分布4個單元，每個單元高度為(h+t)l,試件橫向總長度為4l(不計算縱梁寬度，因其不產生變形)。拉力測試儀所采集到的為每個樣本對應的力-位移離散點，對數據進行線性擬合，由擬合直線的斜率求得結構的彈性模量Ex

(17)

其中：F為拉力；δl為樣本在拉力F作用下產生的位移。

求得該結構的面內橫向無量綱化等效彈性模量Exn=Ex/E，其中：Exnv，Exnu，Exnt分別為V型、U型和梯形結構的無量綱化等效彈性模量。

1.4 面內伸縮特性比較

1.4.1 面內伸縮特性算例和實驗驗證

如圖7，8所示，V型結構面內橫向無量綱等效模量隨著t的增大而增大，隨著h增大而減小。可以看出，理論推導、ANSYS數值仿真以及實驗測試結果比較一致，進一步證實了理論模型的準確性。

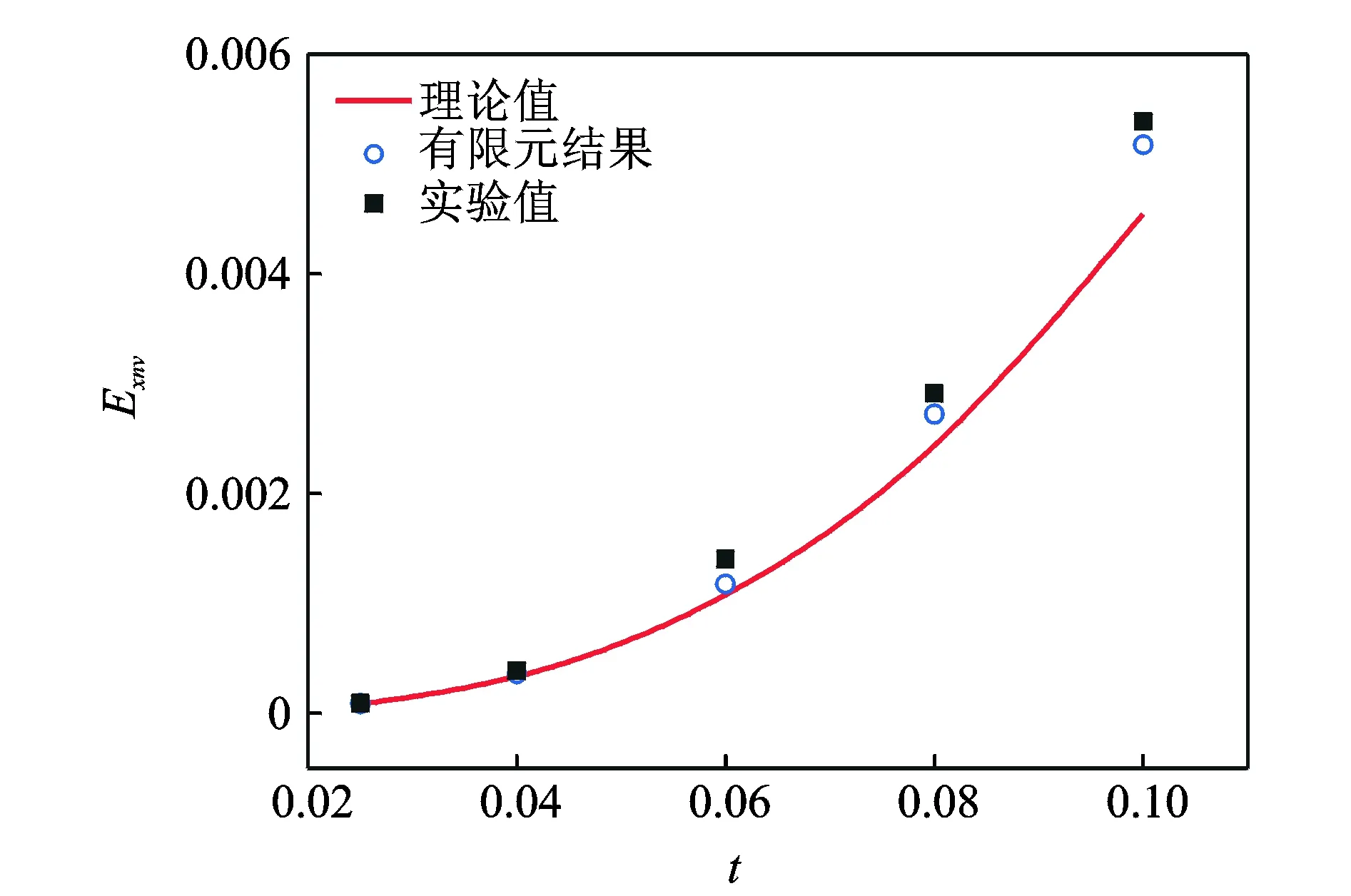
圖7 Exnv隨t的變化關系(V型結構) Fig.7 Exnv versus t(V-type)

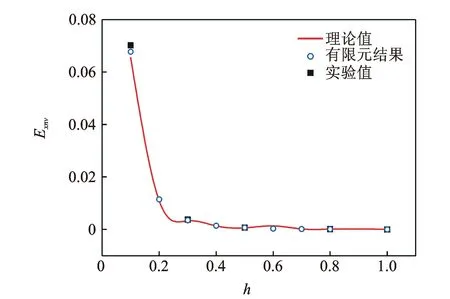
圖8 Exnv隨h的變化關系(V型結構)Fig.8 Exnv versus h (V-type)

1.4.2 3種結構面內伸縮特性比較

從圖9(a)和圖9(b)可以看出，3種結構的面內橫向無量綱化等效彈性模量隨著參數的變化趨勢基本一致：隨著高度系數h的增加而減小；隨著壁厚系數t的增加而增加。在參數相同的情況下，結構的面內橫向無量綱化等效彈性模量按照從大到小的順利排列依次為V型、U型和梯形。該結果表明在相同尺寸參數條件下，V形結構在這3種結構中具有最差的面內伸縮特性；反之，梯形結構具有最佳的面內伸縮特性。在同樣的變形需求下，梯形結構所消耗的變形能量最少。如圖9(c)所示，由于梯形結構多一個參數k，其面內橫向無量綱化等效彈性模量隨著k增大而減小，意味著梯形結構的面內伸縮特性的可調節性更強。

圖9 t,h,k分別對結構橫向等效彈性模量Exn的影響比較Fig.9 Comparison of influence of t, h, k to dimensionless equivalent elastic modulus of the three structures (Exn versus t，h，k)

圖10 ANSYS仿真:V型結構面法向加載情況Fig.10 ANSYS simulation: loading in normal direction (V-type)

2 3種構型蜂窩支撐結構面法向變形能力分析

2.1 基于ANSYS仿真的結構面法向剛度計算

由于蜂窩結構的面法向承載特性相比于面內伸縮變形更為復雜，因此采用有限元方法對其進行分析。利用ANSYS建立3種支撐結構的參數化模型和載荷分布。圖10為V型結構面法向加載示意圖。設定結構的邊界條件為四周固支，載荷條件為面法向均布載荷。面法向仿真模型與面內拉伸實驗試件尺寸一致，采用4×4的單元分布，橫向兩個單元間加有縱梁。在結構面法向加載中，縱梁作為結

構的一部分必須考慮在內，單個試件原始橫向長度LT為4l加上3倍的縱梁寬度tl=2 mm，即LT=4l+3tl=126 mm。ANSYS仿真計算均在結構原長度下進行，縱梁長度統一取200 mm，不同參數結構的中心線在縱向位置保持一致。為與結構實際受載情況相統一，將相同面積(200×126 mm2)蒙皮所受面法向載荷平均分布到支撐結構上，即將支撐結構所受的面法向載荷等效為其支撐的蒙皮表面氣動載荷。利用ANSYS求解在相同等效蒙皮氣動載荷(Pe=200 Pa)作用下，結構的面法向最大位移Dn隨其幾何參數變化的情況。

圖11為t,h,k對結構面法向最大位移的影響。如圖11(a)所示，隨著t的增大，3種結構的面法向最大位移逐漸減小，意味著結構的面法向剛度隨著t增大而增大。如圖11(b)所示，隨著h的增大，3種結構的面法向最大位移同樣增大，即結構的面法向剛度隨著h增大而減小。如圖11(c)所示，由于梯形結構多一個參數k，面法向最大位移隨著k增大而增大，但增大比例不明顯，說明k對面內剛度影響遠遠大于其對面法向剛度的影響。相同參數條件下(k>0.1)與面內剛度相似，面法向剛度從大到小依次為V型、U型和梯形。

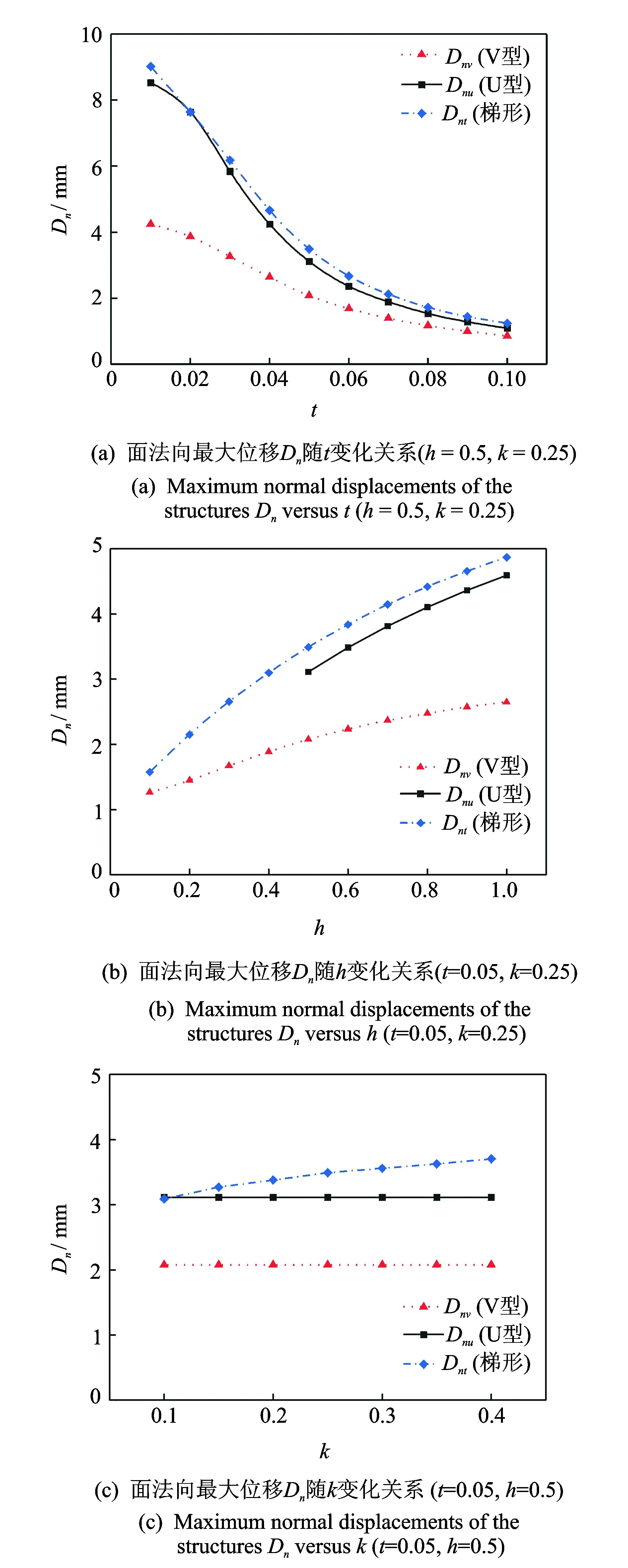
圖11 t, h, k對結構面法向最大位移的影響Fig.11 Maximum normal displacements of the structures versus t, h and k

由以上分析可知，對于蒙皮支撐結構的面內伸縮變形能力較強的結構，其面法向承載能力較弱；而面法向承載能力較強的結構，其面內伸縮變形能力較弱。為解決這個矛盾，一方面，在選擇合適的蒙皮支撐結構時，需要綜合考慮機翼的變形驅動能力和飛行過程中蒙皮的負載情況。當機翼變形驅動能力較強或飛行過程中蒙皮負載較大時，可以考慮采用V型面內變形能力較弱但面法向承載能力較強的蒙皮支撐結構；反之，可以選擇U型和梯形蒙皮支撐結構。另一方面，可以通過對結構進形進一步的參數優化，綜合考慮機翼的變形驅動能力和飛行過程中的蒙皮負載，通過選擇合理的結構形狀參數，獲得同時能夠滿足這兩方面要求的蒙皮結構。

2.2 面法向加載實驗

如圖12所示，由于實驗導軌寬度為160 mm，實驗試件的縱向寬度取160 mm，沙箱寬度為150 mm，幾何參數t=0.05，h=0.5，k=0.25。將結構試件的支撐座一端固定在平臺上，另一端固定在滑塊上。縱梁兩端固支在導軌上。沙箱也設計成活動空間(可改變容積)，用激光測距儀測量試件中心處的面法向位移。試件表面鋪上0.2 mm的硅膠蒙皮，其面法向剛度遠遠小于試件結構。由于激光測距儀精度僅為1 mm，實驗過程中，通過不斷加載直到激光測距儀讀數發生改變，記錄一次沙子的質量和試件中心的面法向位移。分別測量試件在原始長度(LT=126 mm)和119%長度(LT=150 mm)下中心點的位移隨載荷的變化情況。針對3種結構的試件實際尺寸和約束情況重新進行ANSYS仿真，如圖13所示。

圖12 面法向實驗設備、加載與測量Fig.12 Experimental equipment, loading and measurement

圖13 與實驗條件一致的ANSYS仿真(V型結構面法向受載情況和計算結果)Fig.13 ANSYS simulation consistent with the experiment(out of plane loading and calculation results of the V-type structure)

實驗結果如圖14所示，由于初始組裝蒙皮和支撐結構時存在殘余應力，使得支撐結構產生一定的法向變形，導致實驗結果在初始階段斜率較大，隨著載荷的不斷加大，3種支撐結構在實際面法向載荷下的變形趨勢與ANSYS仿真結果逐漸接近，基本隨蒙皮表面壓強增大基本呈線性變化。圖15為試件在原始長度(100%)和拉伸后長度(119%)下中心點的最大位移隨載荷的變化比較。在同樣參數條件下，面法向最大位移大小依次為梯形、U型和V型，說明面法向剛度大小依次為V型、U型和梯形，這與ANSYS仿真結果一致。值得注意的是，3種結構拉伸后的面法向剛度都有較大的提升。

圖14 3種結構面法向最大位移實驗值與有限元仿真結果比較Fig.14 Comparison of maximum normal displacements of the three structures between FEA and experimental results

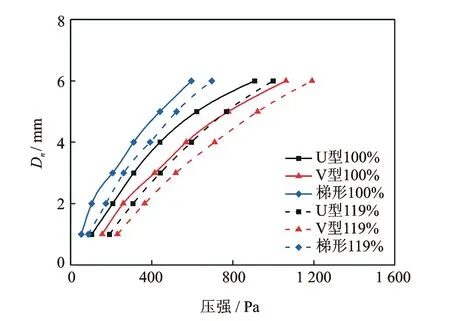
圖15 3種結構拉伸前后面法向位移最大值比較Fig.15 Comparison of maximum normal displacements of the three structures before and after stretching

如表1所示，在產生單位法向位移變形下，承受的壓強平均提高了30%～60%，且承受壓強提升比例從高到低依次為梯形、U型和V型，這與未變形時面法向剛度大小排列相反。這說明面內變形能力較弱的結構形狀在拉伸后面法向剛度的提升比例較大。

表1 面內拉伸前后蒙皮承受的平均表面壓強比較

Tab.1 Average surface pressure of the flexible skin before and after stretching

構型每產生1mm位移蒙皮所承受的平均表面壓強/Pa未拉伸(100%)拉伸后(119%)承受壓強提升/%U型1459.862179.7249.31V型1962.712541.0829.47梯形585.42922.5857.59

3 結 論

1) V型、U型和梯形3種柔性蒙皮支撐結構的面內橫向無量綱化等效彈性模量隨著壁厚系數t的增加而增加，隨著h或k的增加而減小。

2) 同樣參數條件下，面內橫向彈性模量的大小依次為V型、U型和梯形。在同樣的變形需求下，梯形結構所消耗的變形能量最少，其面內橫向彈性模量變化區間最大，可選取的范圍最廣。

3) 3種結構的面法向剛度與3個參數(t，h，k)的關系與面內剛度類似。對于蒙皮支撐結構的面內伸縮變形能力較強的結構，其面法向承載能力較弱；而面法向承載能力較強的結構，其面內伸縮變形能力較弱。

4) 3種結構拉伸后的面法向剛度都有較大提升，在產生相同的面法向位移情況下，承受的壓強平均提高了30%～60%，且面內變形能力較弱的結構形狀在拉伸后面法向剛度的提升比例較大。

[1] Jha A K, Kudva J N. Morphing aircraft concepts, classification, and chanllenges[C]∥Proceedings of SPIE-Smart Structures and Materials 2004: Industrial and Commercial Application of Smart Structures Technologies. Bellingham:SPIE, 2004,5388:213-224.

[2] Thill C, Etches J, Bond I, et al. Morphing skins[J]. The Aeronautical Journal, 2008,112(1129):117-139.

[3] Thill C, Etches J A, Bond I P, et al. Composite corrugated structures for morphing wing skin applications[J]. Smart Materials and Structures, 2010,19(12):124009.

[4] Popov A V, Labib M, Fays J, et al. Closed-loop control simulations on a morphing wing[J]. Journal of Aircraft, 2008,45(5):1794-1803.

[5] Barbarino S, Bilgen O, Ajaj R M, et al. A review of morphing aircraft[J]. Journal of Intelligent Material Systems and Structures, 2011,22(9):823-877.

[6] Weisshaar T A. Morphing aircraft systems: historical perspectives and future challenges[J]. Journal of Aircraft, 2013,50(2):337-353.

[7] Sofla A Y N, Meguid S A, Tan K T, et al. Shape morphing of aircraft wing: status and challenges[J]. Materials and Design, 2010,31(3):1284-1292.

[8] Reich G W, Sanders B, Joo J J. Development of skins for morphing aircraft applications via topology optimization[J]. Journal of Intelligent Material Systems and Structures,2007,20:1-13.

[9] Popov A V, Grigorie T L, Botez R M, et al. Modeling and testing of a morphing wing in open-loop architecture[J]. Journal of Aircraft, 2010,47(3):917-923.

[10]Grigorie T L, Botez R M. New adaptive controller method for SMA hysteresis modelling of a morphing wing[J]. Aeronautical Journal, 2010,114(1151):1-13.

[11]Coutu D, Brailovski V, Terriault P. Promising benefits of an active-extrados morphing laminar wing[J]. Journal of Aircraft, 2009,46(2):730-731.

[12]Barbarino S, Ameduri S, Lecce L. Wing shape control through an SMA-based device[J]. Journal of Intelligent Material Systems and Structures, 2009,20(3):283-296.

[13]Mukherjee S, Ganguli R. A dragonfly inspired flapping wing actuated by electro active polymers[J]. Smart Structures and Systems, 2010,6(7):867-887.

[14]Bhandari B, Lee G, Ahn S. A review on IPMC material as actuators and sensors: fabrications, characteristics and applications[J]. International Journal of Precision Engineering and Manufacturing, 2012,13(1):141-163.

[15]Olympio K R, Gandhi F. Flexible skins for morphing aircraft using cellular honeycomb cores[J]. Journal of Intelligent Material Systems and Structures, 2010,21(17):1719-1735.

[16]Olympio K R, Gandhi F. Zero-ν cellular honeycomb flexible skins for one-dimensional wing morphing[C]∥48thAIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics,and Materials Conference. Honolulu,Hawaii: [s.n.],2007.

[17]Bubert E A, Woods B K S, Keejoo L, et al. Design and fabrication of a passive 1D morphing aircraft skin[J]. Journal of Intelligent Material Systems and Structures, 2010,21(17):1699-1717.

[18]魯超,李永新,董二寶,等.零泊松比蜂窩等效彈性模量研究[J].材料工程,2013,12(15):80-84.

Lu Chao, Li Yongxin, Dong Erbao, et al. Equicalent elastic modulus of zero poisson′s ratio honeycomb core[J]. Journal of Materials Engineering, 2013,12(15):80-84. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.01.003

*國家自然科學基金資助項目(51605140)；江蘇省自然科學基金資助項目(BK20150802)；中央高校基本科研業務費專項資金資助項目(2015B02914)

2015-01-13；

2015-04-24

TB332； TB214.6； TH140； TH122

沈元，男，1986年2月生，博士生。主要研究方向為飛行器設計和空氣動力學。 E-mail: 297084462@qq.com 通信作者簡介：朱華，男，1978年8月生，博士、副研究員。主要研究方向為機械設計及理論、超聲電機技術和變體機翼技術。 E-mail：hzhu103@nuaa．edu．cn