離心力影響條件下的履帶車滑移轉向性能分析*

2017-03-15 12:26:01高學亮鄧兆印

振動、測試與診斷 2017年1期

董超, 成凱, 高學亮, 郗元, 鄧兆印

(1.吉林大學機械科學與工程學院長春，130022) (2.吉林大學汽車仿真與控制國家重點實驗室長春，130022)(3.長春發電設備總廠長春，130022)

董超1, 成凱1, 高學亮2, 郗元1, 鄧兆印3

(1.吉林大學機械科學與工程學院長春，130022) (2.吉林大學汽車仿真與控制國家重點實驗室長春，130022)(3.長春發電設備總廠長春，130022)

針對傳統履帶車轉向力學模型不考慮離心力的影響，為了準確計算履帶車實際轉向過程中的各個轉向性能參數，在深入研究履帶車轉向機理的基礎上，建立了綜合考慮離心力和履帶滑移/滑轉等影響因素下的履帶車轉向數學模型，并以某一具體車型為例進行了數值求解。研究結果表明：車輛轉向過程中產生的離心力會對轉向性能產生影響，與傳統轉向模型分析結果相比，考慮離心力影響時的履帶接地段壓力呈現梯形狀分布并非傳統上認為的均勻分布；車輛在黏性度大的土壤上行駛時履帶的滑移/滑轉也會影響轉向性能。實車試驗也驗證了模型的正確性。該研究成果為履帶車的設計與優化以及平穩轉向控制等提供理論依據。

履帶車；離心力；轉向半徑；滑移率；驅動力

引言

履帶行走系統作為特種工程車輛常采用的行走方式，因其具有良好的道路適應能力、高機動性以及優越的越野性能，被廣泛運用于農業、林業、國防和建筑等領域。如何提高履帶車的機動性能已經成為特種工程車輛技術革新的必然趨勢[1-2]。其中，轉向性能作為履帶車機動性的一個重要標志，已經引起了廣泛關注。目前，對履帶車轉向性能的研究方法大致分為兩類：a.采用數學相關理論方法建立車輛轉向模型進行求解分析，如：文獻[3]建立了履帶車轉向性能預測模型；程軍偉等[4]采用數學理論建立了履帶打滑條件下的車輛轉向模型；成凱等[5]建立了鉸接式履帶車行駛轉向及車體作俯仰運動時的數學模型等；b.采用多體動力學仿真軟件建立履帶車的虛擬樣機模型進行仿真分析，如：文獻[6]采用Recurdyn軟件建立了四履帶車輛轉向模型，通過虛擬樣機仿真技術得到了車輛的驅動力隨轉向半徑和履帶寬度的變化規律；成凱等[7]利用Ansys軟件對鉸接式履帶車處于轉向工況條件下的關鍵零部件進行了有限元分析；馬星國等[8]采用虛擬樣機技術對高速履帶車轉向性能進行了仿真分析等。雖然上述研究取得了階段性成果，但是建立的轉向理論模型均未考慮離心力對車輛轉向性能的影響。工程實踐證明，履帶車在實際轉向過程中，車體產生的離心力嚴重影響車輛轉向的平穩性，特別對于高速轉向時此現象更為明顯。因此，采用考慮離心力的轉向模型來分析履帶車的轉向性能比傳統方法具有現實意義。

筆者在研究履帶車轉向機理的基礎上，建立了綜合考慮離心力、履帶滑移/滑轉條件下的履帶車轉向數學模型，推導出履帶車滑移轉向過程中的各個運動學與動力學參數的計算公式。以某一具體車型為例進行了求解與試驗,對比結果表明了所建模型的正確性。

1 履帶車滑移轉向過程中運動學關系

履帶車差速轉向時，車體繞轉向中心Os勻速轉向。理想情況下，內外兩側履帶的速度瞬心Osi(i=1,2)與履帶的幾何中心Oi(i=1,2)重合,但實際轉向時由于履帶的滑移/滑轉使履帶的速度瞬心Osi(i=1,2)偏離履帶的幾何中心Oi(i=1,2)產生橫向和縱向偏移量Ai和di(i=1,2)[9]。同時,轉向過程中車輛作圓周運動產生的離心力FL使得車體質心Oc偏離車體的幾何中心O產生橫向和縱向偏移量Cx和Cy。離心力的橫向分量影響著內外兩側履帶的垂直載荷分配;離心力的縱向分量影響著履帶縱向上的垂直載荷分配，如圖1所示。運動學模型,圖1中坐標系xOy為全局坐標系,OxOy為坐標原點;L,b,B分別為履帶的長度和寬度以及車體的寬度;Os為車輛實際轉向中心;Oc為車體的質心,車輛的實際轉向半徑R為轉向中心Os到車體質心Oc的距離losoc;Osi(i=1,2)為內外兩側履帶的速度瞬心;Oi(i=1，2)為內外兩側履帶的幾何中心;β為側滑角。

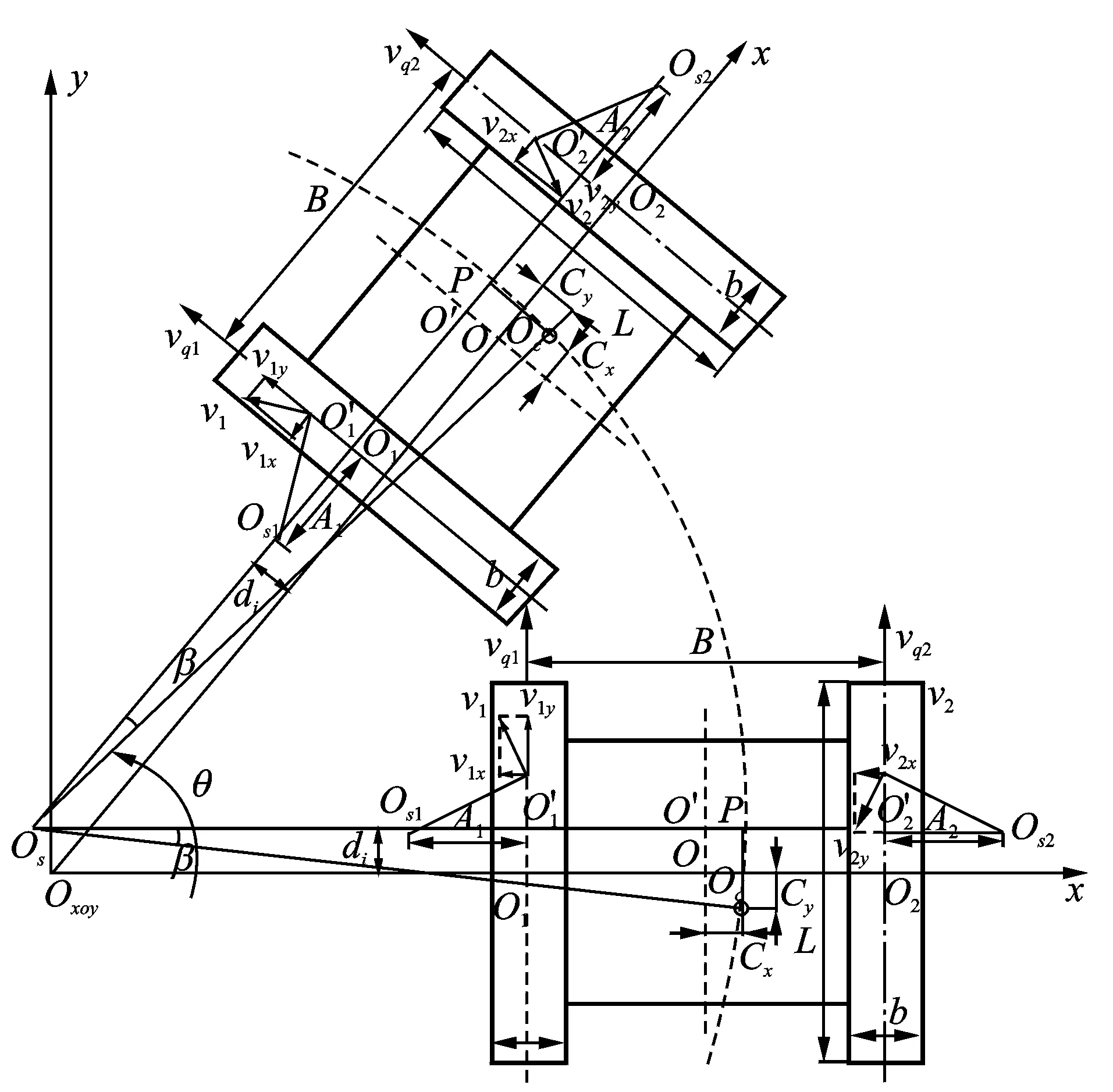
圖1 履帶車滑移轉向運動學模型Fig.1 The caterpillar skid steer kinematic model

履帶車轉向時內外兩側履帶中心線Oi′(i=1,2)處的牽引速度vo′i為

(1)

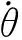
由于車輛轉向過程中履帶出現了滑移/滑轉現象，因此履帶僅有Oi′(i=1,2)處的卷繞速度與理論速度相等[10]，即

(2)

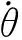
根據圖1中的運動學關系可以求得履帶在滑移/滑轉條件下車輛的實際轉向半徑為

(3)

其中：D為車體質心Oc到轉向中心Os的縱向垂直距離，D=Cy+di；Cy為車體質心的縱向偏移量;di(i=1,2)為內外兩側履帶速度瞬心的縱向偏移量；losp可以根據式(2)求得。

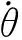
(5)

為了評價履帶的滑移/滑轉程度，筆者采用滑轉率作為評價指標[11]，其表達式為

(6)

其中：vti為履帶的卷繞速度;vo′i為內外兩側履帶的牽引速度，可由式(1)求出。

將vti和vo′i代入式(6)，得到履帶的滑轉率δi為

(7)

2 履帶車滑移轉向過程中動力學關系

為了便于研究履帶車滑移轉向時運動學與動力學相關參數的變化規律，作如下假設：a.履帶車在水平面內作勻速轉向，且轉向過程中車輛的行駛阻力系數保持不變;b.不考慮側向土壤對履帶產生推土阻力的影響;c.履帶接地段壓力分布呈連續線性分布，不計履帶張力變化對接地段壓力的影響。

2.1 履帶接地段壓力分布

圖2 離心力影響下的履帶接地段壓力分布情況Fig.2 The pressure distribution of track under the influence of the centrifugal force

履帶車作圓周運動時常伴隨離心力的產生，離心力不僅會影響履帶接地段壓力的分布,如圖2所示,還會使車輛產生側向力矩和橫向擺動角,若車輛的橫向擺動角過大,將嚴重影響行駛的穩定性。因此,在建立履帶車轉向動力學模型時,不可以忽視離心力的影響。根據圖2,分別對履帶受力點IO和IIO處列力矩平衡方程求得內外兩側履帶法向垂直載荷N1和N2分別為

(8)

(9)

其中:v為車速;h為車體質心離地高度;R為轉向半徑;β為側滑角;Cx為車體質心的橫向偏移量；B為車體寬度；m為履帶車的質量。

由式(8)，(9)可知，履帶車滑移轉向時產生的離心力使車體質心發生偏移，使得內側履帶法向載荷減小，外側履帶法向載荷增大。

內外兩側履帶接地段壓力為

其中：b為履帶寬度；L為履帶長度；N1，N2為內外兩側履帶法向垂直載荷；Cy為車體質心的縱向偏移量；y1，y2為內外兩側履帶接地段縱向上任意一點的縱坐標；D為車體質心Oc到轉向中心Os的縱向垂直距離，D=Cy+di。

由式(10)與式(11)可知:履帶車滑移轉向時產生的離心力使履帶接地段壓力分布不均勻,前端接地壓力減小,后端接地壓力變大,總體呈現梯形狀分布而不是傳統上認為的矩形狀均勻分布。

2.2 履帶受到的轉向摩擦阻力

車輛滑移轉向時履帶受到的行駛阻力主要來自地面的摩擦阻力。以履帶的速度瞬心Osi為原點建立局部坐標系，x軸的正方向沿著履帶的橫向方向,y軸的正方向沿著履帶的縱向方向，如圖3所示。

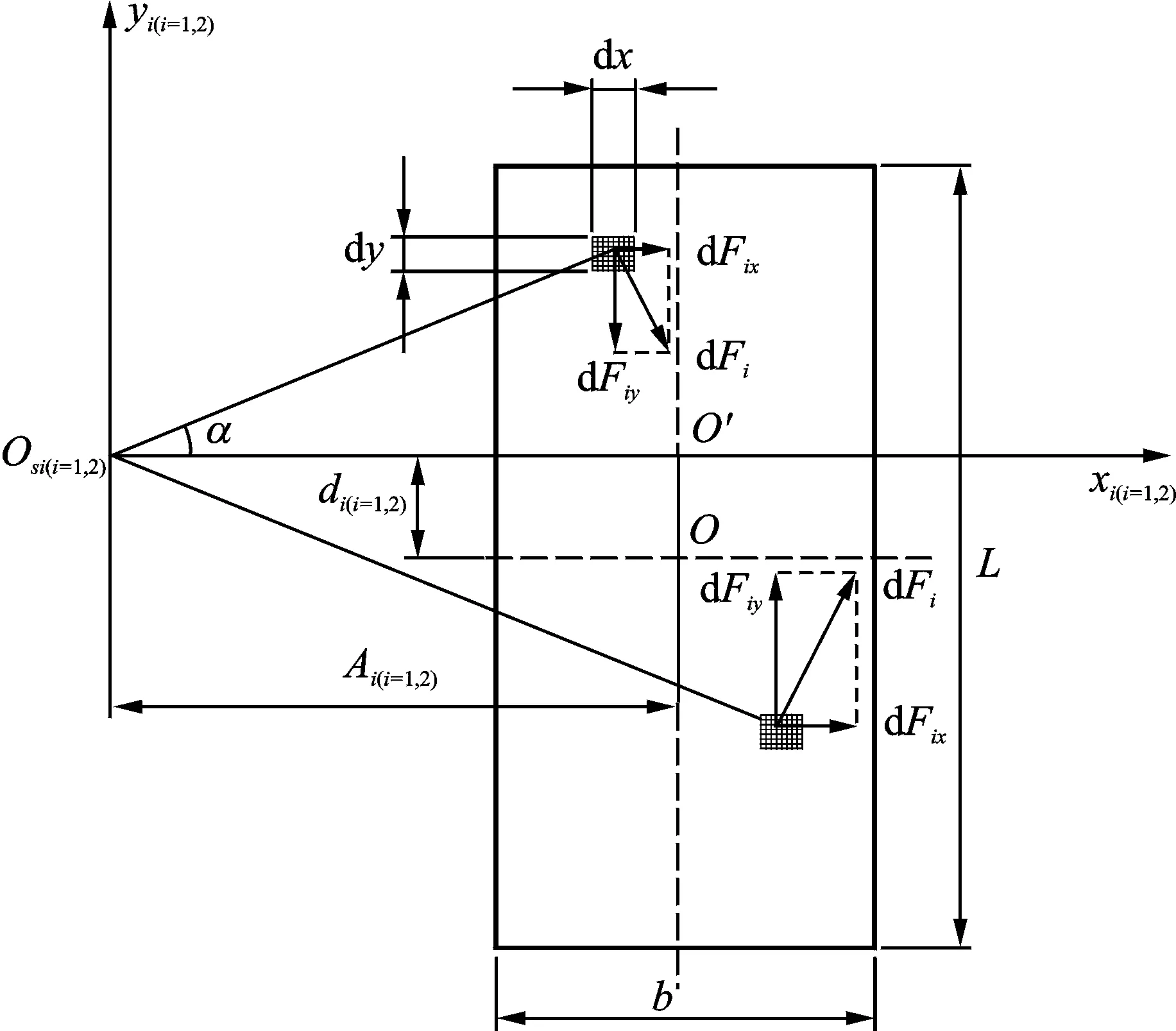
圖3 履帶接地段受到的地面摩擦阻力Fig.3 The friction resistance of the caterpillar

履帶上任取一個微小單元，則車輛轉向時地面對該微小單元產生的摩擦阻力在x軸、y軸上的分量為

dFx i=μpi(yi)sinα

(12)

dFy i=μpi(yi)cosα

(13)

其中:μ為摩擦因數；Pi(yi)(i=1,2)為履帶接地段壓力，可由式(10)，(11)求得；b，L為履帶長度與寬度；α為微小單元與履帶的速度瞬心之間的夾角。

對式(12)，(13)積分，得到地面對履帶產生的摩擦阻力在x軸、y軸方向上的分量分別為

地面對履帶產生的轉向阻力矩為

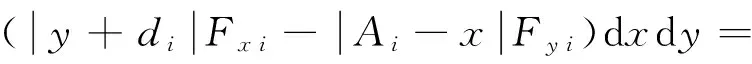
(16)

其中：b，L為履帶的長度與寬度；Ai(i=1，2)為內外兩側履帶速度瞬心的橫向偏移量；di(i=1，2)為內外兩側履帶速度瞬心的縱向偏移量；μ為摩擦因數；Pi(yi)為履帶接地段壓力。

2.3 履帶受到的土壤沉陷阻力

根據Bekker土壤承載理論[12-13]，彈塑性土壤的變形量與土壤承載的關系為

(17)

履帶車轉向過程中，履帶需要克服土壤沉陷量作功，履帶克服土壤沉陷量作功為

(18)

對式(18)進行積分，求得履帶車轉向過程中履帶克服土壤沉陷量所作的功為

(19)

根據功能原理Wi=FciL，得到車輛轉向時履帶所受到的土壤沉陷阻力為

(20)

其中：Z0為土壤的沉陷量；Kc為土壤內聚力模量；Kφ為土壤內摩擦力模量；n為土壤變形指數。

從式(17)，(20)可知：土壤的沉陷量和履帶受到的土壤沉陷阻力是由履帶的接地段壓力和土壤的物理屬性共同決定的，履帶車滑移轉向時產生的離心力使履帶接地段壓力分布不均勻，前端接地壓力小，后端接地壓力大，因此實際履帶接地段的土壤沉陷量和受到的土壤沉陷阻力也是不均勻分布的，履帶前端部分的土壤沉陷量和所受到的土壤沉陷阻力小于后端部分。

2.4 履帶車滑移轉向動力學模型

基于上述假設，履帶車滑移轉向時受到的阻力主要來自地面和車體內部。由式(14),(15)可知，影響車輛轉向摩擦阻力的主要因素是履帶的接地壓力和摩擦因數。假設車輛轉向過程中的地面摩擦因數不發生變化，這樣決定車輛轉向摩擦阻力的因素只有履帶的接地壓力。由于履帶車滑移轉向時產生的離心力使履帶接地段壓力前端小、后端大，導致履帶受到的轉向摩擦阻力呈不均勻分布，沿著履帶縱向方向上的轉向摩擦阻力以前端小、后端大的方式分布，如圖3所示。沿履帶橫向方向上的轉向摩擦阻力以梯形狀方式分布，如圖4所示。

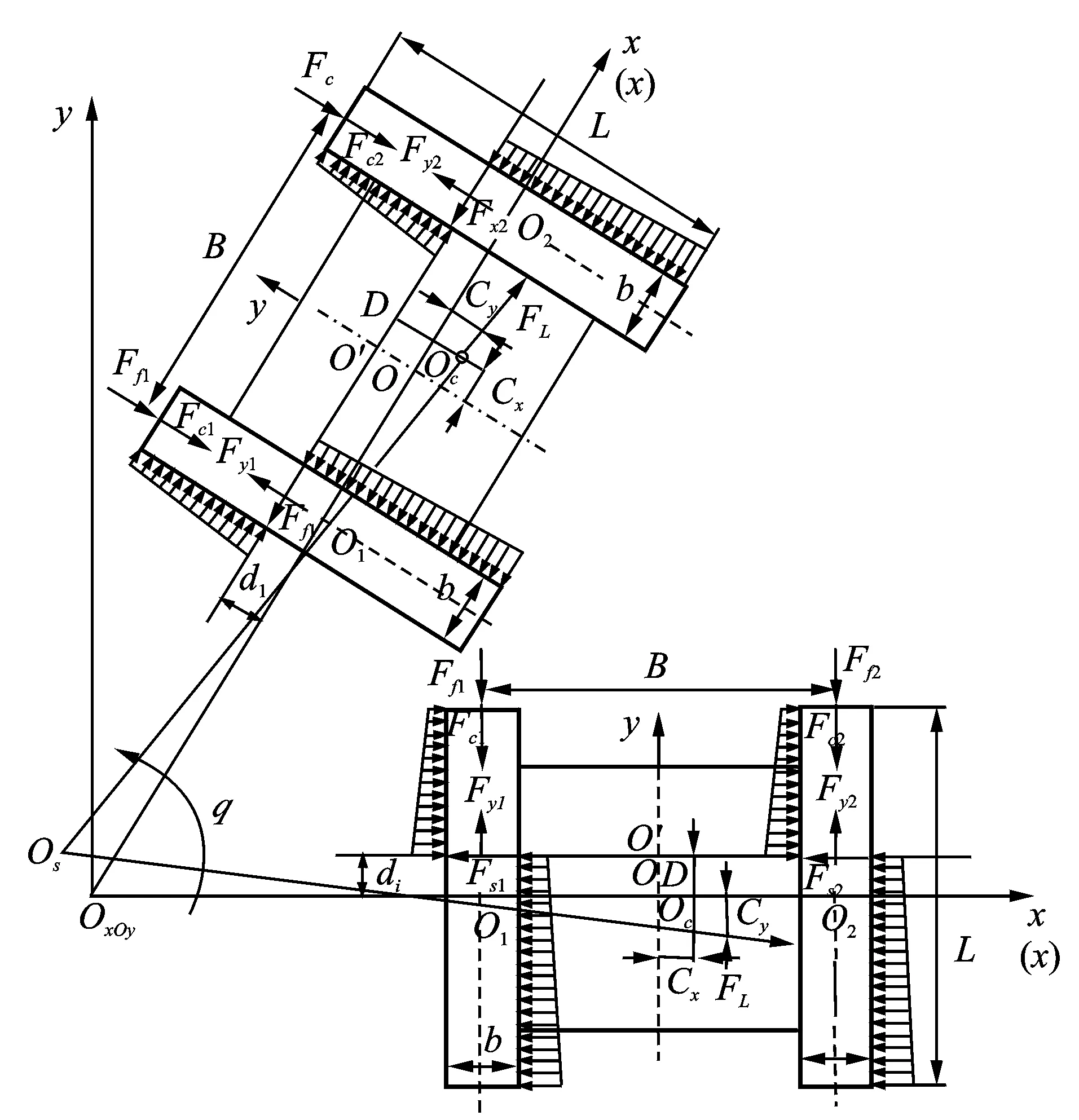
圖4 履帶車滑移轉向動力學模型Fig.4 The caterpillar skid steer dynamics model

根據車輛平穩轉向時履帶受力平衡原理，得到平衡方程組為

(21)

其中:Fx1,Fx2,Fy1,Fy2為內外兩側履帶受到的地面摩擦阻力在x軸、y軸方向上的分量；Fc1，Fc2為內外兩側履帶受到的土壤沉陷阻力；β為側滑角；D為車體質心Oc到轉向中心Os的縱向垂直距離，D=Cy+di；v為車速；m為車輛質量；B為車寬；R為轉向半徑，根據式(4)求得；Mq1，Mq2為車輛轉向時內外兩側履帶所需要提供的驅動力矩，可以通過內外兩側履帶縱向上所受到的力對O′取力矩求得；Ffi(i=1，2)為車體內部阻力，可根據Ffi=fNi，f=0.08求得，Ni可以根據式(8)與式(9)求得。

當給定車速、履帶車的結構參數、內外兩側履帶的牽引速度以及土壤參數時，采用數值迭代法可以求出式(21)中的3個未知數Ai(i=1,2)和di，進而得到履帶車轉向過程中的運動學和動力學參數。

3 實例分析

以國內某企業生產的履帶車為例進行數值求解分析，選用車型結構尺寸如表1所示。設定車輛行駛路面為黏性土壤，物理參數[14]如表2所示。

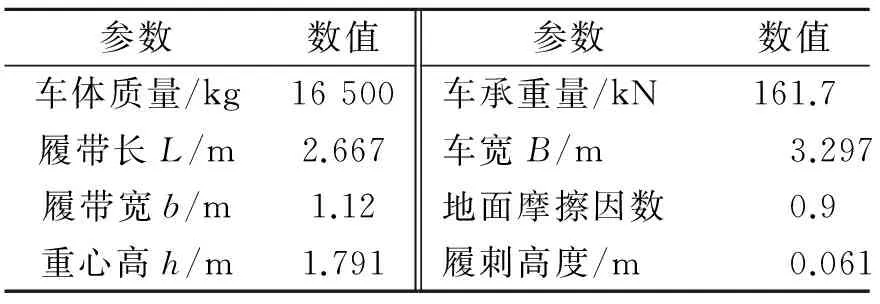
表1 履帶車結構尺寸參數

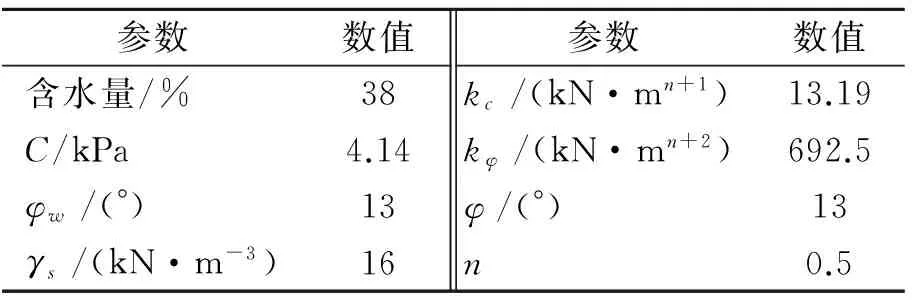
表2 黏性土壤參數[14]

將表1，2中的參數代入式(1)～(21)，求得履帶車轉向過程中運動學和動力學相關參數的變化規律。

3.1 履帶車滑移轉向過程中的運動學分析

3.1.1 車體質心偏移與履帶的速度瞬心偏移對車輛轉向半徑的影響

圖5為車體質心偏移對轉向半徑的影響。可以看出：車體質心偏移會對轉向半徑產生一定的影響，隨著車體質心橫向偏移量的增加，轉向半徑也增加且呈現線性增加的趨勢；隨著車體質心縱向偏移量的增加，轉向半徑也增加，但是其增加趨勢表現為非線性增加。此外，車體質心橫向偏移量對轉向半徑的影響效果大于縱向偏移量對其的影響效果。

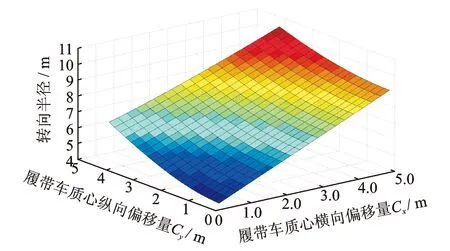
圖5 車體質心偏移量對轉向半徑的影響Fig.5 Tracked vehicle centroid offset affects turning radius

圖6為履帶的速度瞬心偏移對轉向半徑的影響。可以看出：內外兩側履帶的速度瞬心橫向偏移均會對轉向半徑產生影響，隨著內側履帶的速度瞬心橫向偏移量的增加，履帶車的轉向半徑逐漸減小且呈現非線性減小的趨勢；隨著外側履帶的速度瞬心橫向偏移量的增加，履帶車的轉向半徑逐漸增加，呈現出線性增加的趨勢。

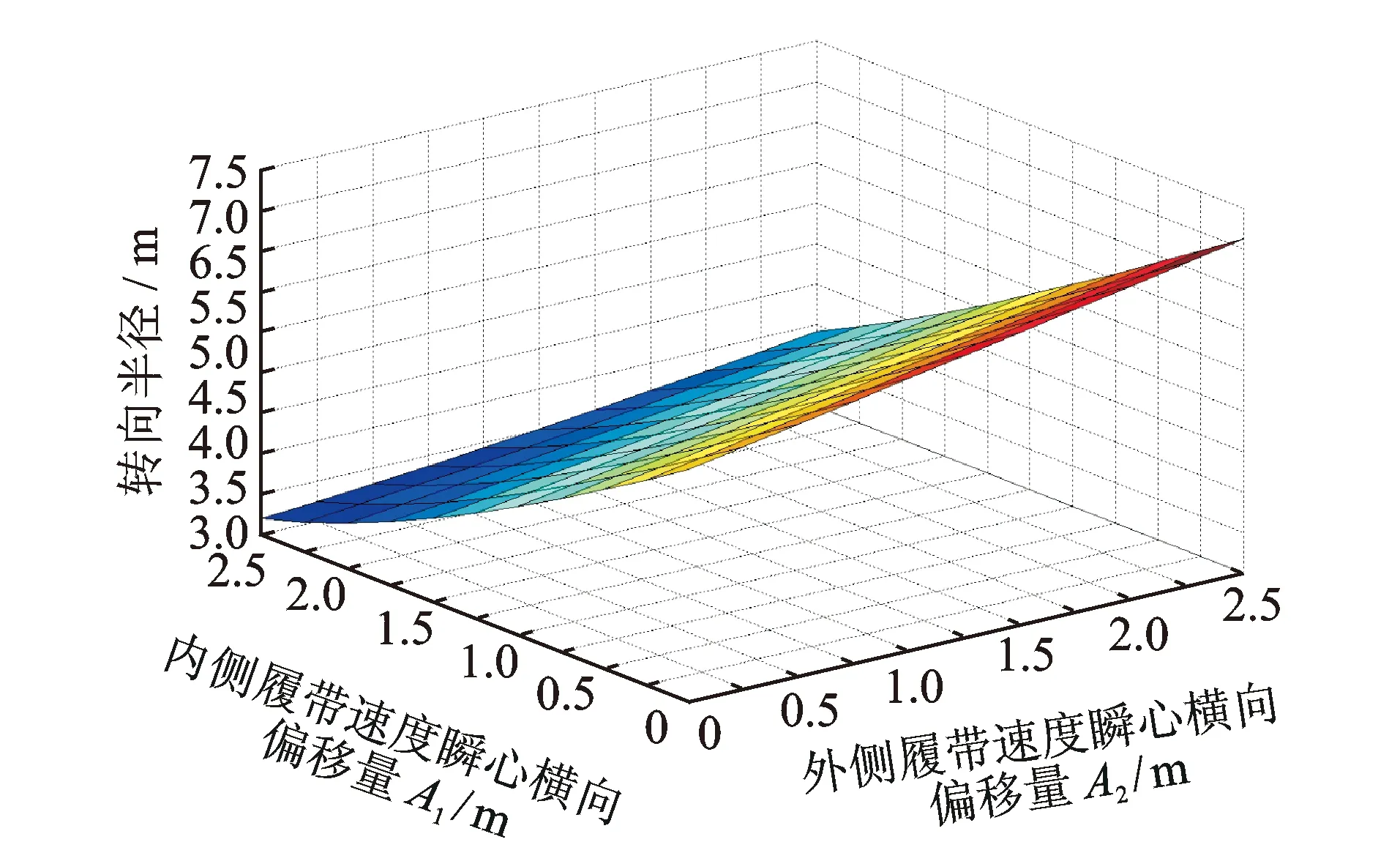
圖6 履帶的速度瞬心偏移量對轉向半徑的影響Fig.6 The crawler instantaneous offset affects turning radius

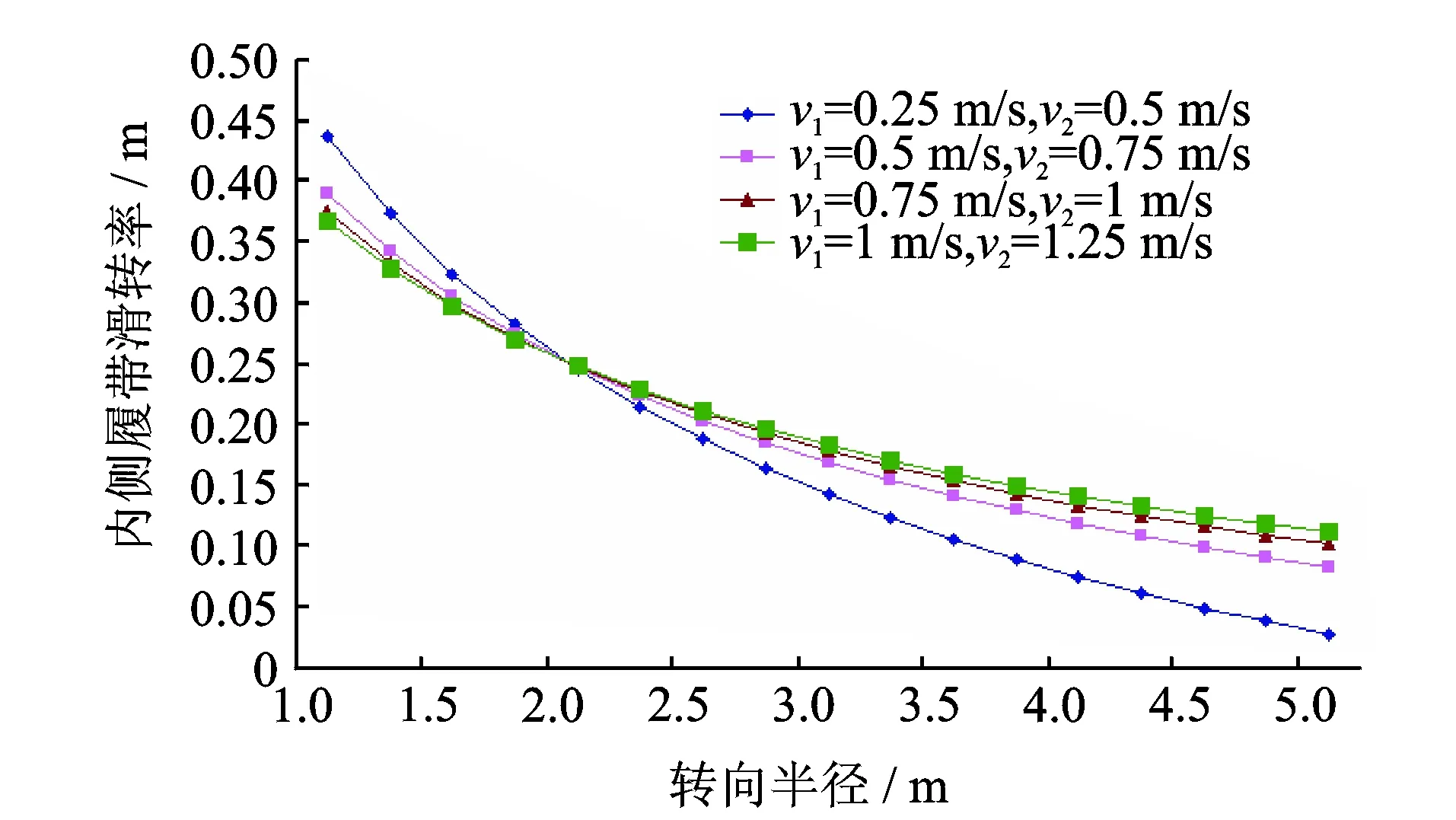
圖7 不同車速和轉向半徑下內側履帶滑轉率變化曲線Fig.7 The lateral slip rate change curve of insides crawler under different speed,different turning radius

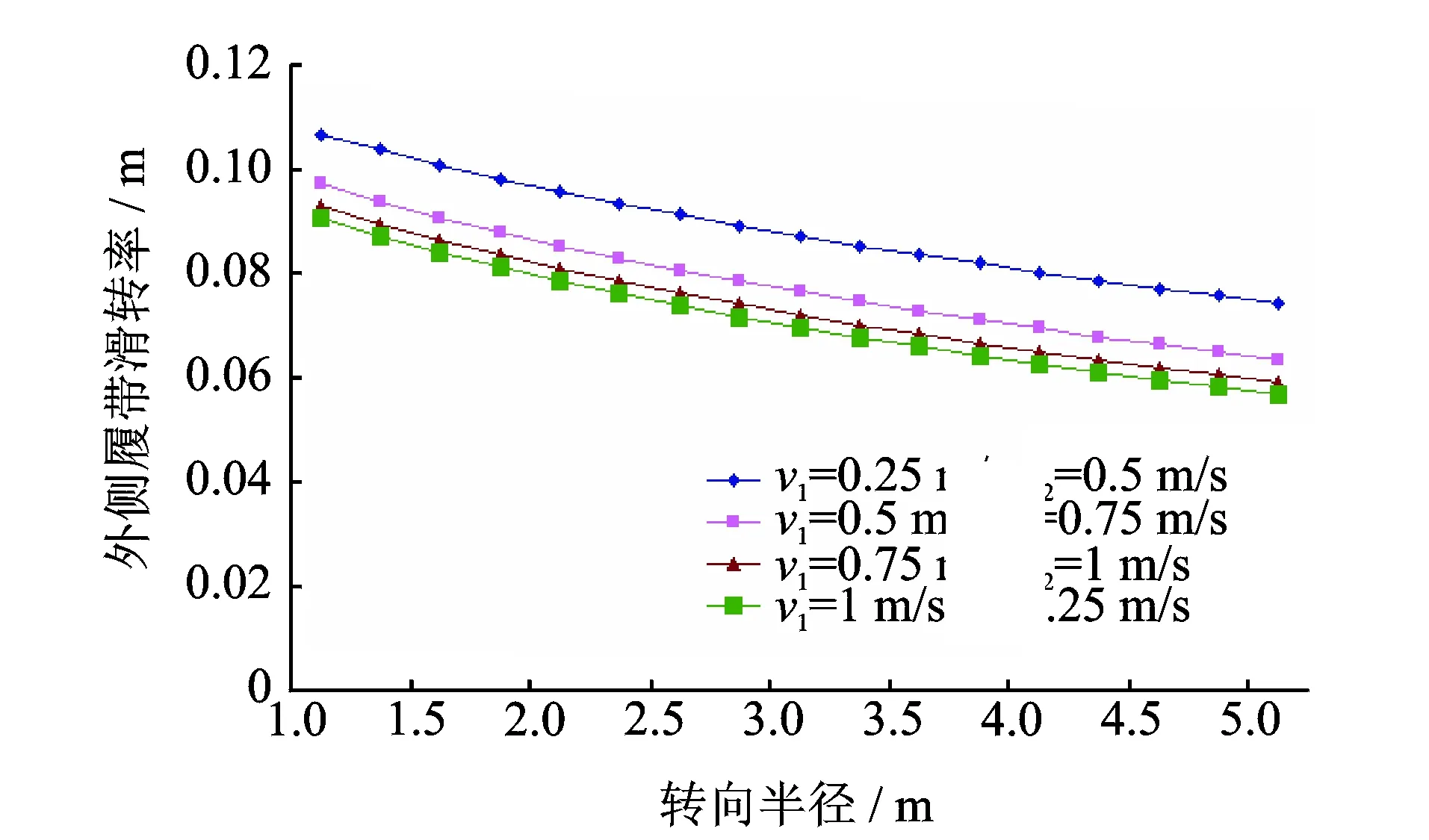
圖8 不同車速和轉向半徑下外側履帶滑轉率變化曲線Fig.8 The lateral slip rate change curve of outsides crawler under different speed,different turning radius

3.1.2 不同車速和轉向半徑條件下內外兩側履帶滑轉率的變化規律

圖7和圖8為不同車速和轉向半徑與內外兩側履帶滑轉率之間的變化關系。可以看出：隨著轉向半徑的增加，內外兩側履帶的滑轉率均減小，但是內側履帶的滑移現象要比外側履帶的滑移現象更為嚴重，并且內側履帶的滑轉率下降程度大于外側履帶的滑轉率下降程度。履帶車采用高速行駛時，車速對履帶滑轉率的影響效果較小。履帶車低速行駛時，車速對履帶滑轉率有較大的影響。

3.2 履帶車滑移轉向過程中的動力學分析

3.2.1 履帶車滑移轉向時內外兩側履帶接地段壓力分布特性

從式(10),(11)可以看出：內外兩側履帶接地段壓力是關于履帶縱向長度yi(i=1,2)的函數，為了研究履帶接地段的壓力分布特性，筆者以計算主動輪、7個支重輪和導向輪接地中心處的壓力為例進行論述。選用的分析樣車履帶結構布置形式如圖9所示。

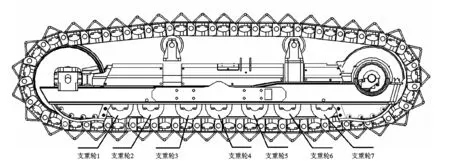
圖9 履帶結構示意圖Fig.9 The track structural of vehicle

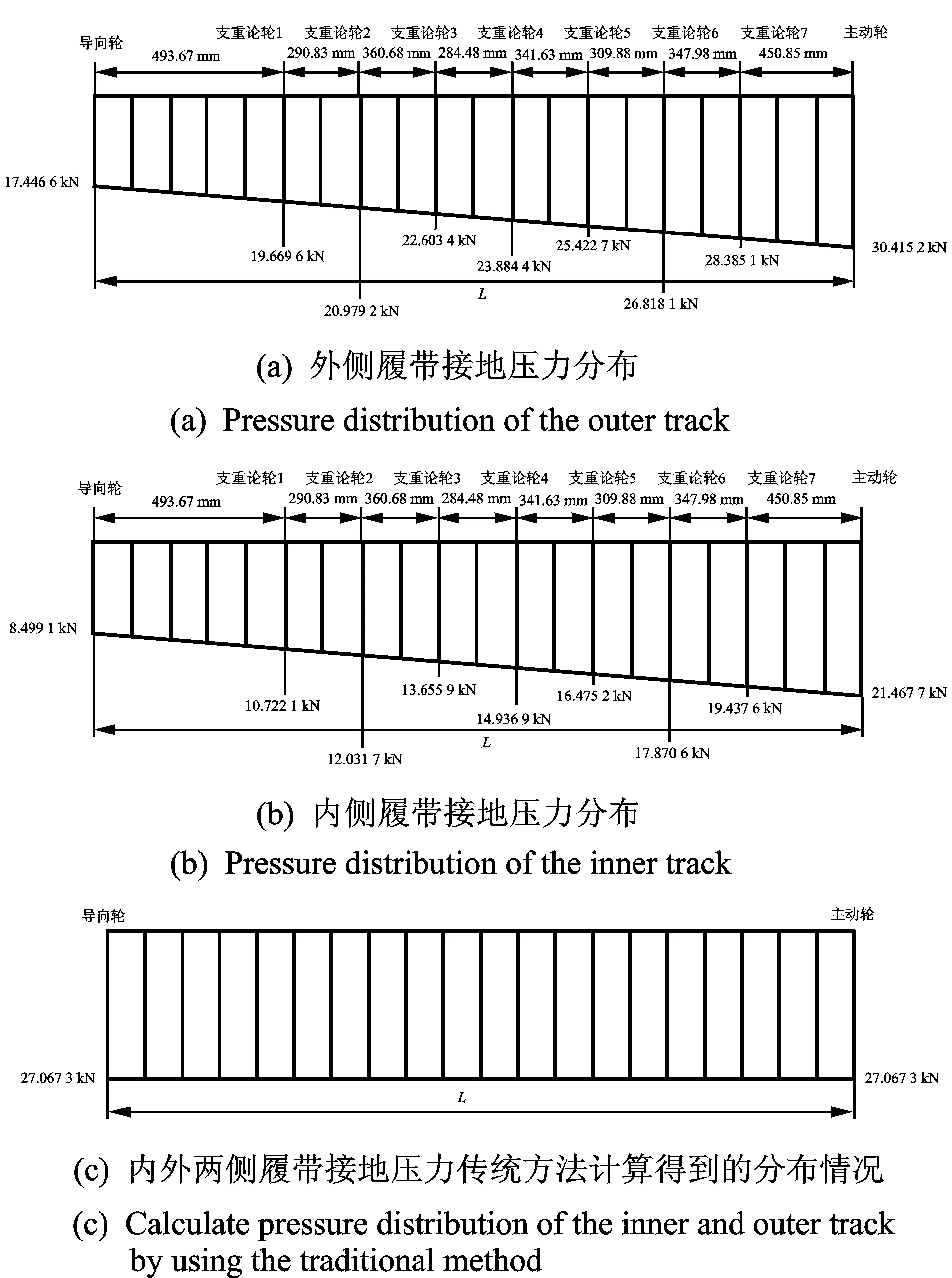
圖10 內外兩側履帶接地壓力分布狀態Fig.10 The pressure distribution of the both sides of the track

圖10為履帶車在車速v=2 m/s，轉向半徑R=5 m的條件下內外兩側履帶接地段壓力分布特性。可以看出：a.車輛轉向時內外兩側履帶接地段壓力分布不均勻，外側履帶接地段壓力總體大于內側履帶接地段壓力，這是由于車輛轉向過程中產生的離心力使車體質心向外偏離，引起外側履帶法向載荷增大，內側履帶法向載荷減小；b.同一履帶沿縱向方向上的接地段壓力分布也不是均勻的，而是履帶前端接地段壓力小，后端接地段壓力大，總體呈現出梯形狀分布形式，不是傳統上認為的矩形狀分布，造成這一現象的原因是車輛轉向過程中產生的離心力使車體質心向車尾偏移，引起履帶前端接地段壓力減小，后端接地段壓力增大。

3.2.2 履帶的速度瞬心偏移對轉向摩擦阻力影響

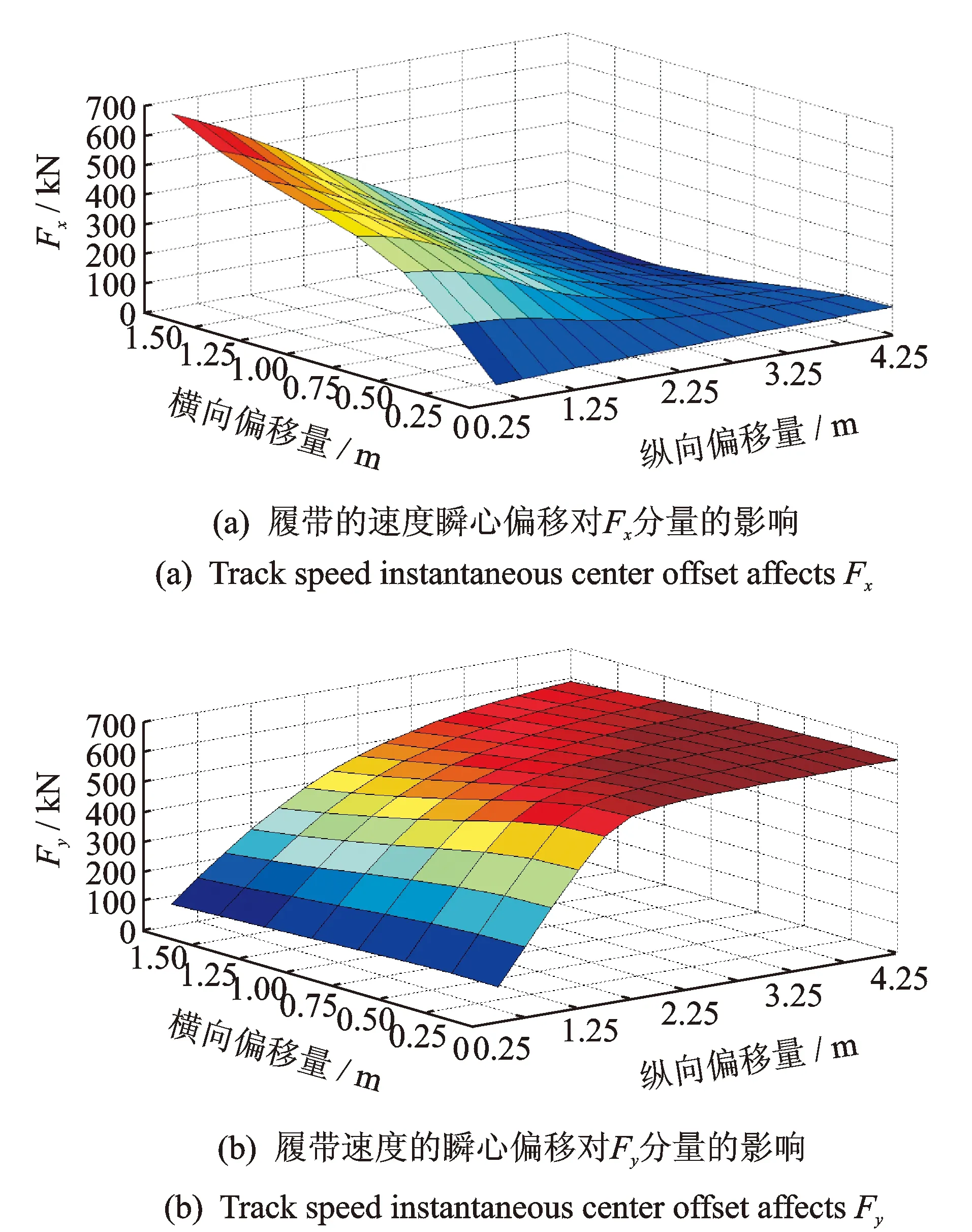
圖11 履帶的速度瞬心偏移對轉向摩擦阻力的影響Fig.11 Track speed instantaneous center offset affects the steering friction

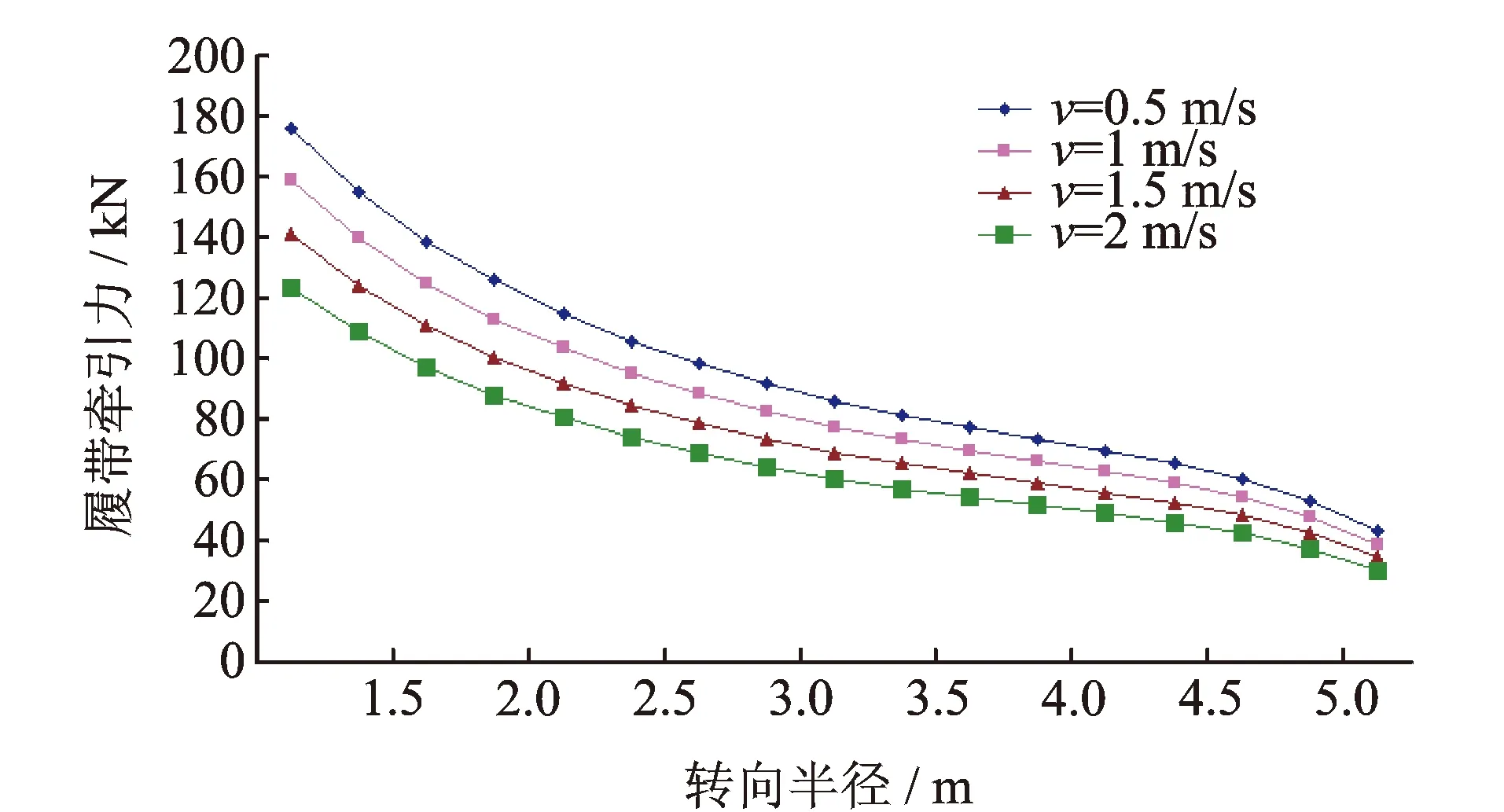
圖12 不同車速和轉向半徑條件下履帶牽引力變化曲線Fig.12 The traction change curve of crawler under different speed and different turning radius

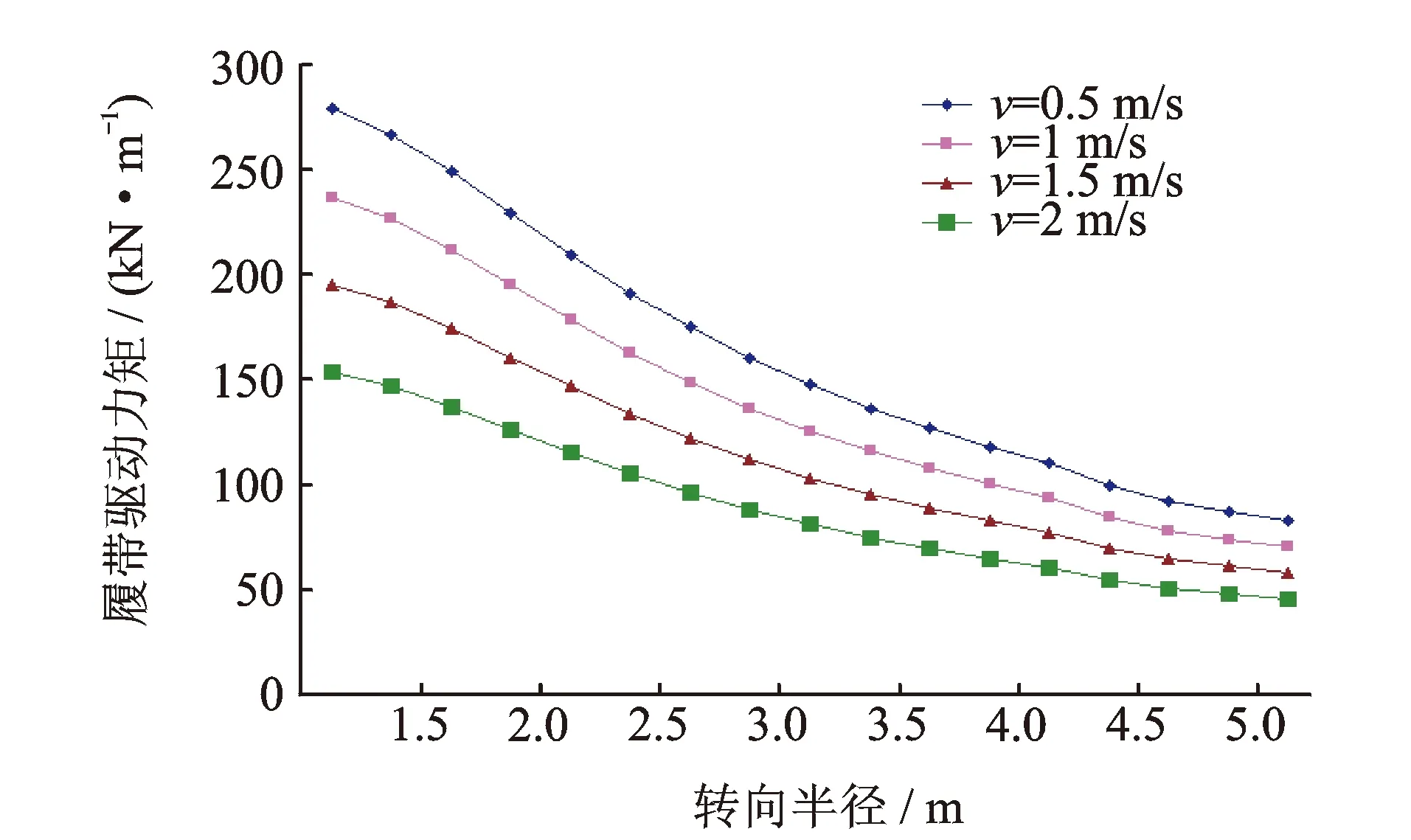
圖13 不同車速和轉向半徑條件下履帶驅動力矩變化曲線Fig.13 The driving torque change curve of crawler under different speed and different turning radius

圖11為履帶的速度瞬心偏移對轉向摩擦阻力的影響。從圖11(a)可看出：履帶速度瞬心的橫向偏移量與縱向偏移量均會對轉向摩擦阻力在x方向上的分量Fx產生較大影響，隨著橫向偏移量的增加，Fx值增大；隨著縱向偏移量增加，Fx值減小。從圖11(b)可看出：轉向摩擦阻力在y方向上的分量Fy隨縱向偏移量的增加而減小，隨橫向偏移量的增加而增大。但是橫向偏移量對Fy的影響效果更加明顯，隨著橫向偏移量的增加，Fy值急劇增加且增長幅度較大，當橫向偏移量達1.75 m時，Fy值逐漸趨于穩定狀態。可見：履帶的速度瞬心偏移對轉向摩擦阻力有較大的影響，這說明履帶的滑移/滑轉對車輛的轉向性能有較大的影響，因此在建立履帶車轉向力學模型時不可以忽略履帶的滑移/滑轉。

3.2.3 不同車速和轉向半徑條件下履帶的牽引力和驅動力矩的變化規律

圖12，13為車輛在不同車速和轉向半徑條件下履帶的牽引力和驅動力矩的變化曲線。可以看出，隨著轉向半徑的增加，履帶的牽引力和驅動力矩均減小，這與文獻[15-16]的研究結果一致。從圖12可知：隨著車輛轉向半徑的增加，履帶的牽引力逐漸減小；在離心力的影響下，車輛處于高速轉向時履帶的牽引力比處于低速轉向時的小；車輛處于小半徑轉向時，由于受到離心力的較大影響，使履帶的牽引力發生了較大變化。從圖13可知：履帶的驅動力矩隨著轉向半徑的增加而減小，并且車速對履帶的驅動力矩有較大的影響效果。從式(21)可知:履帶車的結構尺寸、行駛路況、轉向半徑和車速等都是影響牽引力和驅動力矩的因素。

4 試驗驗證

為了驗證建立的履帶車轉向數學模型的正確性，以某一履帶車為例進行實車試驗,試驗樣車如圖14所示。試驗場地選擇黏性土壤，試驗過程中車輛以II檔(v=7.2 km/h)的速度勻速穩態轉向，整個試驗過程中特別要求發動機始終近似處于勻速穩定運轉。

采用基于光電傳感器的轉速測量系統測量內外兩側履帶主動輪的轉速，測量結果分別為vq1=1.86 m/s,vq2=2.78 m/s；動力輸出軸兩側安裝盤式轉矩傳感器測量轉矩,該傳感器具有存儲數據功能；采用基于GPS的車輛行駛軌跡測量系統測量車輛的轉向軌跡和轉向速度等;采用電子羅盤測量車輛的轉向角度，整個試驗過程中數據采集由NI公司生產的數據采集系統完成。試驗測量結果與理論計算值對比如表3所示。

圖14 試驗選用的樣車Fig.14 The selected tracked vehicle for test

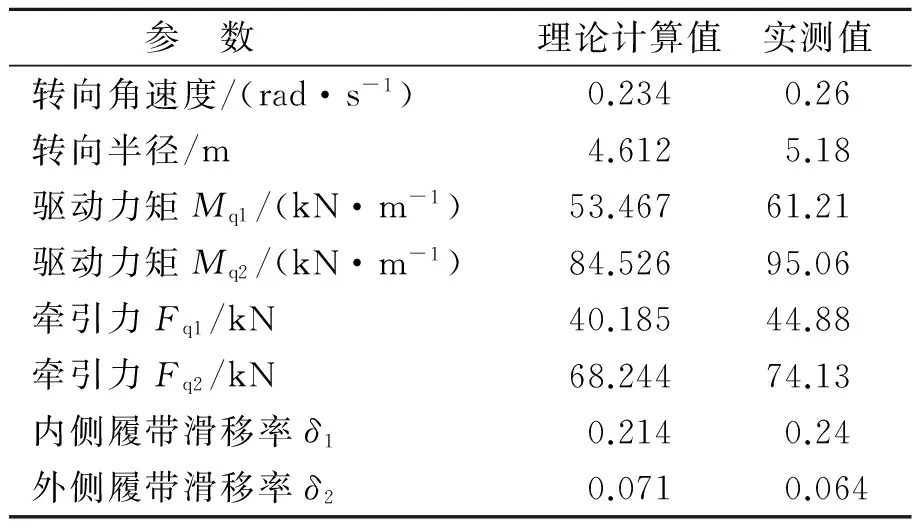
參數理論計算值實測值轉向角速度/(rad·s-1)0.2340.26轉向半徑/m4.6125.18驅動力矩Mq1/(kN·m-1)53.46761.21驅動力矩Mq2/(kN·m-1)84.52695.06牽引力Fq1/kN40.18544.88牽引力Fq2/kN68.24474.13內側履帶滑移率δ10.2140.24外側履帶滑移率δ20.0710.064

可以發現:理論模型的計算值與試驗測量值之間的誤差不超過15%，說明計算結果與實測結果較為接近，驗證了所建模型的正確性。

5 結論

1) 在綜合考慮離心力和履帶滑移/滑轉對車輛轉向性能影響的前提下，建立了履帶車滑移轉向數學模型，理論計算結果與實測結果相符表明了所建模型的正確性，可用于研究履帶車滑移轉向過程中運動學與動力學相關參數的變化規律，為履帶的優化與設計以及控制車輛平穩轉向等提供理論參考。

2) 利用所建模型對車輛轉向性能分析結果表明：車輛轉向時產生的離心力對履帶的接地壓力、驅動力及驅動力矩有較大影響，尤其對于高速行駛的履帶車而言此現象更為突出，所以在研究履帶車轉向相關問題時和履帶車實際設計過程中不可以忽略離心力的影響。

3) 對車輛轉向過程中轉向半徑和轉向摩擦阻力的變化規律分析表明：車輛在黏性土壤上行駛時履帶的滑移/滑轉對轉向性能有明顯影響，土壤黏性度越大，影響程度越大。因此在對履帶車轉向性能分析時應明確行駛路況，對于黏性度小的路況可以不計履帶滑移/滑轉的影響，但對于黏性度大的路況，此處理不妥。

[1] Janarthanan B，Padmanabhan C，Sujatha C.Longitudinaldynamics of a tracked vehicle:simulationand experiment[J].Journal of Terramechanics，2012,49(2)：63-72.

[2] 蘇忠亭，徐達，王帥帥.步兵戰車車體結構有限元模型修正[J].振動、測試與診斷,2014,34(6):1148-1153.

Su Zhongting,Xu Da,Wang Shuaishuai.Finite-element model updating for infantry combat vehicle car-body[J].Journal of Vibration,Measurement & Diagnosis,2014,34(6):1148-1153.(in Chinese)

[3] Maclaurin B.A skid steering model using the magic formula[J].Journal of Terramechanics，2011,48:247-263.

[4] 程軍偉，高連華，王紅巖.基于打滑條件下的履帶車輛轉向分析[J].機械工程學報，2006,42(S):192-195.

Cheng Junwei,Gao Lianhua,Wang Hongyan.Steering analysis of tracked vehicles based on skid condition[J].Chinese Journal of Mechanical Engineering, 2006,42(S):192-195.(in Chinese)

[5] 成凱，張俊，曲振東.鉸接履帶車轉向及俯仰性能研究[J].兵工學報,2012,33(2)：134-141.

Cheng Kai，Zhang Jun，Qu Zhendong.Research on the turning and pitching performances of articulated tracked vehicle[J]. Acta Armamentarii, 2012,33(2)：134-141.(in Chinese)

[6] 李勇，姚宗偉，王國強.四履帶車輛轉向性能仿真研究[J].農業機械學報，2011，42(2)：34-38.

Li Yong,Yao Zongwei,Wang Guoqiang.Steering performance simulation of four-tracked vehicle[J].Transactions of the Chinese Society for Agricultural Machinery，2011，42(2)：34-38.(in Chinese)

[7] 成凱，魏小強，李貴助.鉸接履帶式運輸車轉向俯仰裝置強度剛度分析[J].長安大學學報：自然科學版，2013，33(2)：95-100.

Cheng Kai，Wei Xiaoqiang,Li Guizhu.Strength and stiffness analysis of articulated steering and pitching device on the all-terrain articulated tracked carrier[J].Journal of Chang′an University： Natural Science Edition,2013，33(2)：95-100.(in Chinese)

[8] 馬星國，余昊，尤小梅，等.油氣懸掛式履帶車輛高速轉向動力學仿真[J].中國工程機械學報，2014,12(3):229-232.

Ma Xingguo,Yu Hao,You Xiaomei,et al.Dynamical simulation on high-speed steering for oil-gas-suspended tracked vehicles[J].Chinese Journal of Construction Machinery，2014,12(3):229-232.(in Chinese)

[9] 胡際勇.重型履帶車輛軟地面行駛性能研究[D].長春：吉林大學，2012.

[10]王紅巖,王欽龍,芮強.高速履帶車輛轉向過程分析與試驗驗證[J].機械工程學報，2014,50(16):162-171.

Wang Hongyan,Wang Qinlong,Rui Qiang,et al.Analyzing and testing verification the performance about high-speed tracked vehicles in steering process[J].Chinese Journal of Mechanical Engineering,2014,50(16):162-171.(in Chinese)

[11]張克健.車輛地面力學[M].北京：國防工業出版社，2001.

[12]Bekker M G.Introduction to terrain-vehicle systems[M].Ann Arbor:University of Michigan Press，1969.

[13]Quynh L V，張建潤，劉曉波，等.振動壓路機用于不同土壤地面的平順性評價[J].農業工程學報，2013,29(9)：39-47.

Quynh L V,Zhang Jianrun, Liu Xiaobo,et al. Ride comfort evaluation of vibratory roller under different soil ground[J].Transactions of the Chinese Society of Agricultural Engineering, 2013,29(9):39-47.(in Chinese)

[14]左鵬.全地形鉸接履帶車行走系統研究[D].長春：吉林大學,2012.

[15]Merhof W,Hackbarth E M.履帶車輛行駛力學[M].北京：國防工業出版社，1989.

[16]Al-Milli S,Seneviratne L D, Althoefer K.Track-terrain modelling and traversability prediction for tracked vehicles on soft terrain[J].Journal of Terramechanics,2010,47(3):151-160.