五度圈中的音、音列、音階及其數理關系

杜亞雄

摘要：對五度圈中的音、音列、音階及其內在的數理邏輯關系進行探討，指出了從五度圈中相鄰音中所取的數量及其作為不同音級的可能性之間和所含“宮音”數量之間的規律。前者可用“魚合八”“魚合七”“魚合六”加以說明，后者則可用“x（音列或音階中音的數量）-4=宮音數量”的公式進行概括。

關鍵詞：五度圈；音列；數理邏輯

中圖分類號：J613.6 文獻標識碼：A 文章編號：1004-2172（2016）04-0023-05

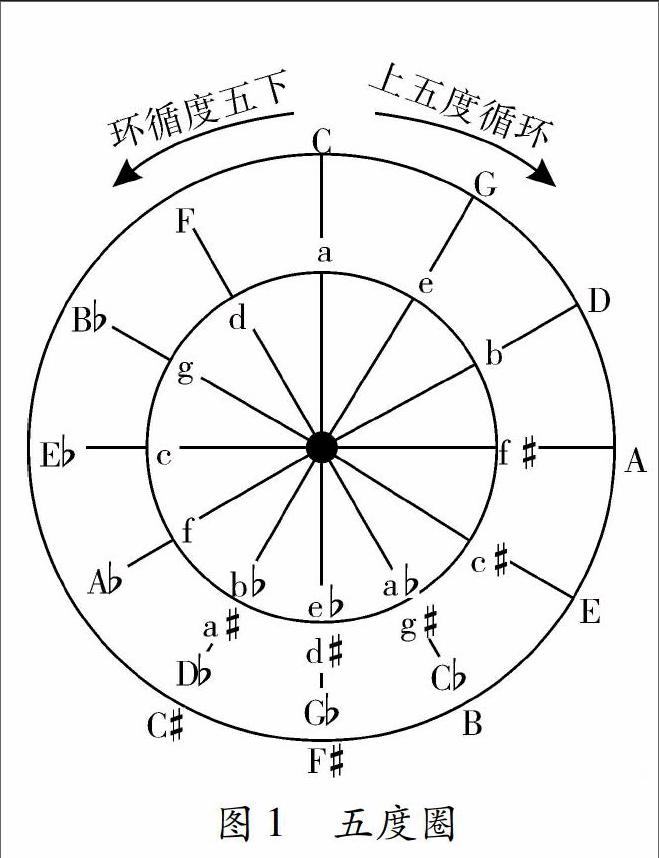
五度圈又稱“五度循環”（circle offifth），即按五度關系，從C音開始，沿順時針或反時針方向，依次歷經其他11個音，最后回到C音的圈。順時針是往屬方向進行上五度循環，反時針是往下屬方向進行下五度循環。如下圖所示：

如果用五度相生律，從C音開始經歷11個音之后，所生出的^#B比C高一個古代音差，即24音分，只能構成“五度螺旋”（spiral of fifth），不能循環，因此中國古代之始發律“黃鐘”不能還原。朱載堉為使“黃鐘”能夠還原，發明十二平均律，并在《樂學新說》一書中首先提出了五度循環的原理。

《尚書》中有“同律度量衡”的說法，《呂氏春秋》中指出：“音樂之所由來者遠矣：生于度量，本于太一。”可見先民很早就注意到了音樂和數學之間的密切關系。十二平均律的發明不僅是音樂學的成果，也是數學的成果，為我們從數理邏輯方面探索樂理中的一些問題開辟了廣闊道路。然而長期以來，我國音樂理論界卻忽視了從這方面進行研究，把一些從數理邏輯上看根本不是問題的問題搞成了問題，且爭論不休，得不出結論。如20世紀80年代，黃翔鵬先生提出“同均三宮”的理論后，音樂學界爭論激烈。有人認為這一理論的提出對我國傳統音樂研究和基本樂理建設都有很深遠的意義。也有人認為“同均三宮”根本就是“假象和錯覺”。目前，音樂學界對此尚未取得共識。

數理邏輯是數學和邏輯學相結合的綜合學科，它用數學方法研究形式邏輯問題，并將推理過程用數學公式進行運算，從而得出結論。本文嘗試采用數學方法對五度圈上的音、音列、音階的關系進行探討，試圖證明一些樂理的基本原理。為便于討論，首先說明有關音、音列、音階和“宮”的概念。

鄭玄說：“宮商角徵羽，雜比曰音，單出曰聲”可見在漢代，單個音級稱為“聲”，若干“聲”放在一起稱為“音”。現代漢語中仍保留了這種用法，如在“五聲音階”和“七聲音階”等詞組中，“聲”指單個音級，“音”由數“聲”構成。現代漢語中的“音”也可指單個音級，如“宮音”“商音”，還可以指某一類曲調，如“花音”“苦音”“歡音”“哭音”。本文中的“音”指單個音級。

歐洲樂理認為多于一個音級，便能構成音階，有二聲音階（ditonic scale）、三聲音階（tritonic scale或trichord）、四聲音階（tetratonic scale或tetrachord）的概念。因有“五行學說”的傳統，我國音樂理論界普遍認為夠“五聲”才能叫“音階”，只有二個、三個或四個音的組合稱為“音列”，本文亦將它們稱為“音列”。

我國音樂理論界一般承認“五聲音階”和“七聲音階”，至于“六聲音階”是不是一個真實、獨立存在的概念，則有爭論。筆者認為“六聲音階”是客觀的存在，本文將討論“五聲”“六聲”和“七聲”三種不同的音階。

中國樂理中所使用“宮”字的意義通常有三：（一）階名之一，即“宮聲”或“宮音”，它歷來被視為眾“音”之首，被稱作“音主”，在中國音樂中具有重要地位。無論是五聲還是七聲音階，一旦宮音的高度位置確定，其它各音（如商、角等）的高度也就都確定下來了。本文中稱“宮”的這層意義為“宮音”。“宮音”統領著下面所說“宮系”。（二）自起始律到相生第六次所得的那一律，七個律位排成的七聲音階構成“一宮”，通常以起始律命名，如“黃鐘宮”“林鐘宮”等。由于我國古代以“正聲音階”為標準，今天以西洋大調式結構相同的“下徵音階”為標準，如果將“黃鐘”相當于西洋音名中的“C”，古代的“黃鐘宮”相當于今天的“G宮”下徵音階而不是“C宮”正聲音階。（三）指與第二項“宮音”高度相同的各五聲或七聲調式構成的“宮系統”。后兩個層面上的“宮”都具有調高的意義，本文都稱為“宮系”。正如前面說的，“宮系”由“宮音”統領，沒有“宮音”，也就沒有“宮系”

一

五度圈中每個“音”在音列、音階中的地位，依靠它與其他“音”的關系決定，其中存在著嚴格的數理關系。

在五度圈上任取一個“音”，它便可能是五聲音階或六、七聲音階中的任何一個音。在五聲音階中有五種可能性，從首調唱名法講（下同），可能是do，可能是re，也可能是mi、sol或la。在六聲音階中有六種可能性，七聲音階中的可能性有七種，可能是do，可能是re，也可能是mi、fa、sol、la或者是ti。此時，不可能明確它是“宮音”還是其他任何音。在用五度圈上相鄰的音構成兩音列、三音列和四音列三種情況下，“宮音”也是不可能確定的。

如果在五度圈上取相鄰的兩個音，這兩個音之間只能構成純五度及其轉位純四度的音程。此時，比起只有一個音來，當作不同音級的可能性便減少一種。如取“C-C”兩音，在五聲音階中有“do-sol”“la-mi”“sol-re”“re-la”四種可能性。在六聲音階中多一種可能性，可能是“fa-do”，也可能是“mi-ti”。在七聲音階中就又多了一種可能性，即“fa-do”和“mi-ti”都有。

如果在五度圈上取相鄰的三個音，這三個音之間可以構成純五度、純四度和大二度、小七度的音程。當作不同音級的可能性比“二音列”更少一種。如取“C-G-D”三個音，在五聲音階中有“do-sol-re”“sol-re-la”“re-la-mi”三種可能性。在六聲音階中也多一種可能性，即可能是“fa-do-sol”，而在七聲音階中就又多了一種可能性，即可能是“la-mi-ti”。黎英海先生在《漢族調式及其和聲》一書中以陜北民歌《繡荷包》為例，指出其中的“g-c-d”三個音可能是“徵-宮-商”、也可能是“商-徵-羽”或“羽-商-角”。因為他認為“在任何調式中宮音總不可省去”，所以說《繡荷包》是徵調式。其實在為這一曲調配和聲時，也不妨把它看成是羽調式或商調式，這樣選擇性多些，色彩也會更為豐富。

如果在五度圈上取相鄰的四個音，它們之間可以構成的音程是純五度、純四度、大二度、小七度、小三度、大六度，比起“三音列”來，作為不同音級的可能性又要更少一種。如取“C-G-D-A”四個音，在五聲音階中有“do-sol-re-la”“sol-re-la-mi”兩種可能性。在六聲音階中多一種可能性，七聲音階中比六聲音階還多一種可能性。黎英海先生曾以一首由G-A-C-D四個音構成的、長江流域的山歌為例，并指出因為曲調中“沒有出現角音”，“可能是徵調，也可能是商調”。按照黎先生“宮音不能省去”的理論，這首歌是“徵調式”。然而，如果在配和聲時，把它商調式來處理，也沒有什么不妥之處。

如果在五度圈上取相鄰的五個音，在第一個音和第五個音之間就會形成一個大三度，這大三度音程就形成了中國樂理中的“宮一角關系”。此時，這五個音作為不同音級的可能性比“四音列”更少一種，在五聲音階的情況下，只有“do-re-mi-sol-la”一種可能性。在六聲音階中多一種可能性，七聲音階中比六聲音階還要多一種。這時，也只有在這時，“宮音”的位置就明確了。

至此，我們便可以發現在五度圈中所取音的數量及其作為不同音級可能性之間的數理邏輯關系，即：音的數量及作為不同音級的可能性的數量相加為音階中的音級數加一。若為七聲音階，其得數應為“8”，六聲音階應為“7”，五聲音階是“6”。如表1、2、3所示：

在我國傳統音樂中，有一種稱為“魚合八”的結構形式，每個樂句都有八個譜字，分兩個部分，第一部分遞增，譜字分別為1-3-5-7，第二部分遞減，譜字數分別為7-5-3-1，兩個部分相加總是8，故名“魚合八”。如譜例1所示：

譜例1

表1、2、3中顯示出的數理邏輯結構與“魚合八”一致，在七聲音階的條件下為“魚合八”，六聲音階為“魚合七”，而五聲音階則是“魚合六”。

二

在五度圈中取相鄰的音構成音列、音階及其所含的“宮音”的數量，也有嚴格的數理邏輯關系，而且和上述五度圈中所取音的數量及構成音級的可能性密切相關。正如前文所述，如果在五度圈中取相鄰的四個音，它們之間不能構成“宮一角”關系，因此會有“do-sol-re-la”“sol-re-la-mi”兩種不同的解釋。然而在五度圈上取相鄰的五個音，在第一個音和第五個音之間就會形成一個大三度，這大三度音程就形成了中國樂理中的“宮-角關系”，這樣“宮音”的位置就定下來了，在五聲音階的條件下，便只能有一種可能性了。

如果在五度圈中取相鄰的六個音，在第一個音和第五個音之間和在第二個音及第六個音之間就能構成兩對“宮-角”關系，便可能有兩“宮音”和與之相應的兩個不同的“宮系”存在于這個六聲音階中，如“c-g-d-a-e-b”即可能是“do-re-mi-fa-sol-la”（G宮）也可能是“do-re-mi-sol-la-ti”（C宮）。這兩種六聲音階中的第一種在歐洲樂理中稱為“自然六聲音階”（natural hexachord），第二種則稱為“硬六聲音階”（hard hexachord）。

譜例2是一首著名的蒙古族民歌，從譜面上看是六聲音階，筆者1987年在匈牙利李斯特音樂學院教學時，曾要求同學們演唱它。匈牙利采用首調唱名法，故同學們將第一小節第一個音符唱“la”。在我國，用首調唱名法演唱第二行時，仍按兩個升號的調來唱，前兩個音符唱“do-fa”。匈牙利學生卻把第二行的第一、二個音符都唱成“do”，因為按照歐洲的“首調唱名法”，從這一小節第二個音起，已轉入一個升號的調，必須要改換唱名法。匈牙利學生的唱法說明，用五度圈中取相鄰的六個音構成的六聲音階，按照歐洲樂理的規范，也可以有兩個“宮音”和兩個“宮系”。

譜例2

如果在五度圈上取相鄰的七個音，在第一個音和第五個音、在第二個音和第六個音和在第三個音和第七個音之間就會形成三個大三度。這三個大三度音程都可以形成“宮一角關系”，在這個七聲音階中便會有三個“宮音”和它們所統領的“宮系”。如“c-g-d-a-e-b-^#f”，即可能是“do-re-mi-fa-sol-la-ti”（G宮）也可能是“do-re-mi-^#fa-sol-la-ti”（C宮）還可能是“do-re-mi-fa-sol-la-bti”（D宮）。這三“宮系”之間“音主”的位置必然是五度圈上的第一、二、三音，它們之間的關系也必然是純五度、純四度和大二度，其實這就是“同均三宮”。關于什么是“均”，黃翔鵬先生說：“在‘五度圈的連續音高序列中摘取七律（古書中叫做‘以七同其數）構成音階（古書中也把七聲音階稱做‘七律），這七個律高所構成的絕對音高位置與各律間相對的音程關系的總和就是‘均。這個定義如果不好理解，我們只好簡單化地說，‘均就是七律在‘五度圈中的位置。”

如果在五度圈上，任選連續的8個音，就可以構成4個大三度音程，它們分別處于第一個音和第五個音、第二個音和第六個音、第三個音和第七個音、第四個音和第八個音之間。如果任選連續的9個音，就可以構成5個大三度音程，它們分別處于第一個音和第五個音、第二個音和第六個音、第三個音和第七個音、第四個音和第八個音、第五個音和第九個音之間。如果任選連續的10個音，就可以構成6個大三度音程。選11個音，就可以構成7個大三度音程。其內在的數理邏輯是五度圈中所取音的數量減去數字4，便構成能夠形成“宮音”和“宮系”的數量。如表4所示：

如果在五度圈上，任選連續的11個律位，可構建7個“宮系”。最后生成的5律，在十二平均律的條件下，轉換為等音，就可以建立12個“宮系”。這12“宮系”，就是在西方樂理中12個調。在每個上面建立一個大調和一個小調，就是以圖一中顯示的那些音為主音的24個大小調。

從表4中不難看出，從五度圈上所取的音的數量和能構成“宮音”及其統領的“宮系”的數量成正比，三個數字之間的關系是：“音列”所包含的“音”數量減4，就得到這些“音”可能構建的“宮系”的數量。

小結

“魚合八”“魚合七”“魚合六”以及“同音列數宮系”的現象應當是放之四海而皆準的，古今中外，在采用五度相生律的各民族的音樂中，應當沒有、也不會有例外。

從五度圈中所取的“音”的數目和它們在音列、音階中所充當音級的可能性為反比。所取的“音”的數目越少，可能性越多。所取的“音”的數目越多，可能性則越少。

從五度圈中所取的“音”的數目和出現“宮音”以及由其所統領的“宮系”數目之間為正比，“音”的數目越多，“宮音”的數目越多；低于四個音，“宮音”便不能確定，“宮音”需要有5個音才能確定，之后每增加一個音，就增加一個“宮音”。黃翔鵬先生提出“同均三宮”理論，也應當被包含在“同音列數宮系”的法則中，“同均三宮”的理論只涉及了一個在五度圈上取7個音的情況，并沒有論及取6個音或超過7個音時的情況。

既然“魚合八”“魚合七”“魚合六”以及“同音列數宮系”的現象在中國音樂和歐洲音樂中都存在，就應當在樂理課中介紹，這對音樂理論建設和音樂創作實踐都有會有所裨益。

責任編輯：李姝