基于混沌DESAPSO算法的無(wú)人機(jī)三維航跡規(guī)劃

唐匯禹，彭世蕤，孫經(jīng)蛟，劉香嵐

(空軍預(yù)警學(xué)院，武漢 430019)

【信息科學(xué)與控制工程】

基于混沌DESAPSO算法的無(wú)人機(jī)三維航跡規(guī)劃

唐匯禹，彭世蕤，孫經(jīng)蛟，劉香嵐

(空軍預(yù)警學(xué)院，武漢 430019)

粒子群(PSO)算法易陷入局部最優(yōu)，將其運(yùn)用于無(wú)人機(jī)三維航跡規(guī)劃會(huì)導(dǎo)致航跡品質(zhì)不高，針對(duì)這一問(wèn)題，提出了將差分進(jìn)化(DE)算法、模擬退火(SA)算法嵌入PSO算法中，構(gòu)成混沌差分進(jìn)化模擬退火粒子群(DESAPSO)算法，從三個(gè)方面提高了航跡品質(zhì)：一是利用DE算法的變異、交叉及競(jìng)爭(zhēng)選擇增加種群多樣性；二是利用SA算法概率突跳能力跳出局部最優(yōu)解；三是對(duì)PSO算法參數(shù)進(jìn)行混沌優(yōu)化，進(jìn)一步增強(qiáng)種群多樣性。仿真結(jié)果表明：混沌DESAPSO算法改進(jìn)航跡品質(zhì)效果明顯，獲得了滿意的無(wú)人機(jī)三維航跡。

混沌粒子群；差分進(jìn)化；模擬退火；無(wú)人機(jī)；航跡規(guī)劃

無(wú)人機(jī)航跡規(guī)劃就是在滿足威脅回避、機(jī)動(dòng)性能限制等約束條件下，求得一條從起始點(diǎn)到目標(biāo)點(diǎn)的最優(yōu)或次優(yōu)航跡，其實(shí)質(zhì)為多目標(biāo)優(yōu)化問(wèn)題[1]。而三維航跡規(guī)劃搜索空間巨大，傳統(tǒng)的經(jīng)典算法諸如牛頓法、梯度法等已不適用，取而代之的是現(xiàn)代智能算法，其中具有代表性的包括粒子群算法(PSO)、遺傳算法、蟻群算法和模擬退火算法等[2]。

PSO算法[3]具有實(shí)現(xiàn)容易、計(jì)算精度高、收斂速度快的特點(diǎn)，且其易與其他算法相結(jié)合，衍生出許多性能優(yōu)良的算法。目前，已有許多學(xué)者將標(biāo)準(zhǔn)PSO算法及其改進(jìn)算法運(yùn)用于無(wú)人機(jī)航跡規(guī)劃中，取得了許多成果[4-6]。但標(biāo)準(zhǔn)PSO算法后期易陷入局部最優(yōu)，其根本原因是迭代后期粒子間相似度很高，種群多樣性缺失。為了解決這一問(wèn)題，提高航跡規(guī)劃品質(zhì)，在此從以下三方面來(lái)增加粒子種群多樣性：一是利用差分進(jìn)化算法的變異、交叉及競(jìng)爭(zhēng)選擇操作來(lái)增加種群多樣性，其中變異和交叉算子采用非線性算子保證后期粒子若未能搜尋到全局最優(yōu)解時(shí)，仍具有較高的全局搜索能力；二是利用模擬退火算法的突跳能力增加種群多樣性，跳出局部最優(yōu)找到全局最優(yōu)；三是對(duì)PSO算法的參數(shù)采用混沌序列保證不重復(fù)遍歷整個(gè)空間，進(jìn)一步增強(qiáng)種群多樣性。

將改進(jìn)后的混沌DESAPSO算法運(yùn)用于無(wú)人機(jī)三維航跡規(guī)劃，通過(guò)與其他算法對(duì)比表明該算法性能優(yōu)良。

1 無(wú)人機(jī)三維航跡規(guī)劃建模

1.1 航跡編碼

無(wú)人機(jī)航跡是由離散的導(dǎo)航節(jié)點(diǎn)直線相連而成的線路，算法中每個(gè)粒子的信息代表一條航跡。因此，可假設(shè)粒子數(shù)目為N，每條航跡除起始點(diǎn)和目標(biāo)點(diǎn)外共有m個(gè)導(dǎo)航節(jié)點(diǎn)，整個(gè)種群可表示為：X=[X1,X2,…,XN]T，其中Xi為第i個(gè)粒子的位置。令Xi=[x0,xi1,…，xim,xt,y0,yi1，…，yim,yt,z0,zi1，…，zim,zt]，其中(x0,y0,z0)、(xt,yt,zt)為航跡起始點(diǎn)和目標(biāo)點(diǎn)，(xim,yim,zim)為第i個(gè)粒子中第m個(gè)導(dǎo)航節(jié)點(diǎn)的三維坐標(biāo)。

另外，考慮粒子位置雖可進(jìn)行限制，但粒子運(yùn)動(dòng)是不定方向的、隨機(jī)的，為確保粒子能從起始點(diǎn)朝著目標(biāo)點(diǎn)方向運(yùn)動(dòng)，可采取對(duì)粒子x軸坐標(biāo)進(jìn)行固定均分，即將[x0,xt]均分成(m+1)段，y軸和z軸只做限制，不做均分。粒子在進(jìn)行位置更新和限制時(shí)，只對(duì)y軸和z軸中除起始點(diǎn)和目標(biāo)點(diǎn)外的m個(gè)導(dǎo)航節(jié)點(diǎn)進(jìn)行操作。

1.2 航跡適應(yīng)度函數(shù)

智能優(yōu)化算法運(yùn)用于航跡規(guī)劃，需建立合適的適應(yīng)度函數(shù)，適應(yīng)度函數(shù)值即無(wú)人機(jī)飛行代價(jià)，該值是評(píng)價(jià)航跡優(yōu)劣的唯一指標(biāo)。無(wú)人機(jī)的適應(yīng)度函數(shù)包括兩大方面，分別為機(jī)動(dòng)性能約束和威脅約束。其中，機(jī)動(dòng)性能約束主要包括最大爬升角/下滑角、最大水平轉(zhuǎn)彎角、最大航程、最小步長(zhǎng)、最小轉(zhuǎn)彎半徑；威脅約束主要包括火力威脅、地形威脅和高度威脅。

對(duì)于機(jī)動(dòng)性能約束代價(jià)，可參考文獻(xiàn)[5]。其中最大爬升角/下滑角和最大水平轉(zhuǎn)彎角代價(jià)函數(shù)表達(dá)式相同，最大航程代價(jià)和步長(zhǎng)程度代價(jià)改進(jìn)后分別如式(1)、式(2)所示。

(1)

其中，ltotal為總路程，L為起始點(diǎn)到目標(biāo)點(diǎn)的直線距離，Lmax為無(wú)人機(jī)的最大航程。

(2)

其中，Lstep為步長(zhǎng)程度標(biāo)準(zhǔn)值，Li為相鄰節(jié)點(diǎn)的航跡長(zhǎng)度。

而最小轉(zhuǎn)彎半徑約束，可通過(guò)爬升下滑角/水平轉(zhuǎn)彎角、步長(zhǎng)程度以及高度變化來(lái)合理控制，因此不對(duì)其另行約束，高度變化代價(jià)如式(3)所示：

(3)

其中，Δhi為相鄰節(jié)點(diǎn)的高度變化值，CΔh為安全閾值。

威脅代價(jià)中的雷達(dá)威脅，可參考文獻(xiàn)[7],導(dǎo)彈威脅和高炮威脅可參考文獻(xiàn)[8]，對(duì)三種威脅進(jìn)入禁飛區(qū)的情況，對(duì)式(1)施加懲罰K；地形威脅代價(jià)參考文獻(xiàn)[8]，對(duì)進(jìn)入禁飛區(qū)的情況同樣施加懲罰K，另外將山峰地形等效成圓錐體存在一定誤差，因此設(shè)置無(wú)人機(jī)飛行高度比當(dāng)前地形高度高某一數(shù)值Clim，以此保證安全飛行，如式(4)所示：

(4)

其中，z(x,y)為無(wú)人機(jī)當(dāng)前坐標(biāo)的地形高度，z為無(wú)人機(jī)當(dāng)前高度。

高度威脅可設(shè)置如式(5)所示的代價(jià)函數(shù)。

(5)

其中：z為當(dāng)前飛行高度，Hmin為最小離地高度，Hmax為無(wú)人機(jī)以概率1被發(fā)現(xiàn)的高度。

綜上，對(duì)任意航跡Xi，其航跡總代價(jià)如式(6)所示，通過(guò)設(shè)置不同的權(quán)值可以合理評(píng)價(jià)各代價(jià)對(duì)航跡的影響。

(6)

其中，N為粒子數(shù)；fk為各代價(jià)函數(shù)；M為代價(jià)種類數(shù)，ω1～ωM為相應(yīng)的權(quán)值，其和值為1。

2 混沌DESAPSO算法

2.1DE算法

DE算法[9]包括變異、交叉以及競(jìng)爭(zhēng)選擇3步：首先，對(duì)第t代第i個(gè)粒子中的除開起始點(diǎn)和目標(biāo)點(diǎn)外的y坐標(biāo)和z坐標(biāo)進(jìn)行差分變異得到變異個(gè)體Ui(t+1)：

Ui(t+1)=Xr1,j(t)+F(Xr2,j(t)+Xr3,j(t))

(7)

其中，r1、r2、r3為[1,N]的隨機(jī)整數(shù)，且滿足r1≠r2≠r3≠i，j為除開起始點(diǎn)和目標(biāo)點(diǎn)外的y坐標(biāo)和z坐標(biāo)，F(xiàn)為非線性變異算子，如式(8)所示：

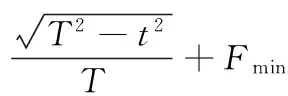
(8)

其中，F(xiàn)max、Fmin分別為變異算子的最大值和最小值，T為最大迭代次數(shù)。

然后，對(duì)產(chǎn)生的變異個(gè)體進(jìn)行交叉操作得到實(shí)驗(yàn)個(gè)體Vi, j(t+1)：

(9)

其中，CR為交叉率，采用如式(10)的非線性變異算子，randni為[m+3,2m+3]和[2m+6,3m+5]間的隨機(jī)整數(shù)，m為前述導(dǎo)航節(jié)點(diǎn)數(shù)，這樣做是保證實(shí)驗(yàn)個(gè)體Vi, j(t+1)至少有一位是由變異個(gè)體Ui, j(t+1)貢獻(xiàn)。

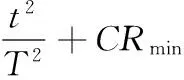
(10)

最后，對(duì)實(shí)驗(yàn)個(gè)體Vi(t+1)和種群個(gè)體Xi(t)進(jìn)行競(jìng)爭(zhēng)選擇得到新一代種群個(gè)體Xi(t+1)：

(11)

2.2 混沌PSO算法

PSO算法起源于群鳥覓食，對(duì)于前述編碼方式，可假設(shè)每個(gè)粒子速度為Vi=(vi1,vi2,…,viN)，粒子個(gè)體的最好位置為Pi=(pi1,pi2,…,piN)，其適應(yīng)值稱為個(gè)體極值，粒子群的最好位置為Pg=(pg1,pg2,…,pgN)，其適應(yīng)值稱為全局極值，粒子依據(jù)下式進(jìn)行速度和位置更新：

(12)

(13)

其中，ω為[0,1]內(nèi)的慣性因子，c1、c2稱為學(xué)習(xí)因子，一般取2；r1、r2為[0,1]內(nèi)變化的隨機(jī)數(shù)，為確保不重復(fù)遍歷整個(gè)搜索空間，可對(duì)參數(shù)r1、r2采取的混沌操作，混沌序列為logistic模型如式(14)。

(14)

2.3SA算法

SA算法[10]起源于固體退火過(guò)程，在采用了如式(15)所示的Metropolis準(zhǔn)則后，算法具有以概率1收斂到全局極值的能力。

(15)

其中，Δf為后一代粒子適應(yīng)值和前一代粒子適應(yīng)值的差值，exp(-Δf/T(t))>rand項(xiàng)是為了保證前期溫度較高時(shí)，即使后一代粒子適應(yīng)值較差，仍具有以較高概率exp(-Δf/T(t))接受裂解的可能，從而跳出局部最優(yōu)。后期隨著溫度降低，粒子接受裂解的可能變得極小，從而逐漸收斂到全局最優(yōu)。要注意的是，后期雖然接受裂解概率極小，但不能排除有接受裂解的可能，因此應(yīng)該實(shí)時(shí)保存迭代過(guò)程中找尋到的歷史最優(yōu)解。T(t)為當(dāng)前迭代溫度，溫度衰減一般采用如式(16)的線性衰減，α為溫度衰減系數(shù)，取值范圍在[0.5,0.99]。

T(t)=α*T(t-1)

(16)

2.4 混沌DESAPSO算法流程

混沌DESAPSO算法是以PSO算法為主流程，主要過(guò)程包括三步：一是利用改進(jìn)的DE算法對(duì)種群進(jìn)行變異、交叉和競(jìng)爭(zhēng)選擇；二是利用混沌參數(shù)r1、r2對(duì)PSO種群進(jìn)行再次遍歷尋優(yōu)；三是利用SA算法的Metropolis準(zhǔn)則促使粒子群跳出局部最優(yōu)，最終收斂到全局最優(yōu)。

混沌DESAPSO算法具體步驟如下：

步驟1:初始化算法所有參數(shù)，包括粒子數(shù)N、最大迭代次數(shù)T、變異因子F、交叉因子CR、慣性權(quán)重ω、學(xué)習(xí)因子c1、c2、r1、r2、以及退火初始溫度T0和溫度衰減系數(shù)α，初始化種群位置和速度，且t=1；

步驟2:計(jì)算每個(gè)粒子的適應(yīng)值，初始化個(gè)體極值pbest和全局極值gbest；

步驟3:迭代開始，按式(7)、式(9)和式(11)對(duì)初始化的粒子種群進(jìn)行變異、交叉和競(jìng)爭(zhēng)選擇，更新個(gè)體極值pbest和全局極值gbest；

步驟4:按式(12)、式(13)對(duì)粒子進(jìn)行速度和位置更新，進(jìn)行速度和位置限制使其不超過(guò)邊界，計(jì)算每個(gè)粒子適應(yīng)值，進(jìn)行個(gè)體極值和全局極值更新；

步驟5:計(jì)算前后代粒子的適應(yīng)值差值Δf，按式(15)進(jìn)行模擬退火操作，按式(16)進(jìn)行降溫操作；

步驟6:判斷t是否小于等于最大迭代次數(shù)T，若是，轉(zhuǎn)到步驟3；若否，算法結(jié)束，輸出最優(yōu)航跡。

3 仿真驗(yàn)證

本文特征地形模型參考文獻(xiàn)[11]，模擬5座山峰，山峰中心坐標(biāo)分別為(40,40)、(50,160)、(100,100)、(140,50)、(160,170)，山高Hi=[2.5,2.8,3.2,2.8,2.5]，無(wú)人機(jī)起點(diǎn)和終點(diǎn)分別為(10,10,2)、(130,110,3)，上述單位均為km。雷達(dá)威脅、導(dǎo)彈威脅以及高拋威脅參數(shù)如表1所示。

表1 威脅信息

分別用PSO算法、SAPSO算法以及混沌DESAPSO算法進(jìn)行無(wú)人機(jī)三維航跡規(guī)劃，各算法獨(dú)立連續(xù)獨(dú)立運(yùn)行30次進(jìn)行分析對(duì)比，混合算法參數(shù)同單一算法參數(shù)全部取相同，算法參數(shù)設(shè)置如下：PSO算法參數(shù)，粒子數(shù)目N=30，最大迭代次數(shù)T=500，慣性權(quán)重ω從0.9線性遞減至0.2，學(xué)習(xí)因子c1=c2=2；SA算法參數(shù)，初始溫度T0=4 000，溫度衰減系數(shù)α=0.98；DE算法參數(shù)，變異因子F從0.7非線性遞減至0.4，交叉因子從0.3非線性遞增至0.8。各算法運(yùn)行結(jié)果如表2所示。

表2 三種算法測(cè)試結(jié)果

從測(cè)試結(jié)果可以看出：PSO算法、SAPSO算法以及混沌DESAPSO三種算法收斂精度和穩(wěn)定性依次不斷提高，表明航跡規(guī)劃品質(zhì)不斷提高；從數(shù)值變化來(lái)看，由于導(dǎo)航節(jié)點(diǎn)少、概率代價(jià)模型數(shù)值小以及對(duì)代價(jià)進(jìn)行了1/13的加權(quán)平均，因此航跡品質(zhì)改善明顯；從平均時(shí)間來(lái)看，前兩種算法復(fù)雜度相近，由于SAPSO算法收斂精度較PSO更高，因此平均耗時(shí)更短，而混沌DESAPSO復(fù)雜度明顯高于前兩種算法，以犧牲時(shí)間為代價(jià)獲得了精度的提升。各算法迭代收斂曲線如圖1(a)所示，局部放大如圖1(b)所示。

由圖1可知，混沌DESAPSO算法收斂速度最快，大約到10代就接近收斂到全局極值，PSO算法次之，SAPSO算法最慢。本文給出PSO算法和混沌DESAPSO算法二維及三維航跡對(duì)比圖，分別如圖2(a)、(b)和圖3(a)、(b)。

由圖2和圖3可知：從二維航跡看，兩種算法都能找到滿足威脅回避、地形回避的可行航跡，且混沌DESAPSO算法能找到更加利用山峰遮蔽的二維航跡；從三維航跡看，混沌DESAPSO算法能找尋到高度更低、更靠近山峰飛行的三維航跡，也因此航跡品質(zhì)更高，驗(yàn)證了航跡改善的有效性。

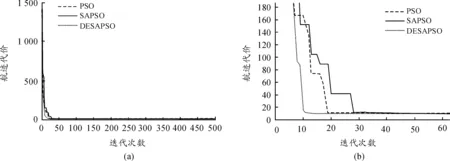
圖1 三種算法迭代收斂曲線

圖2 PSO和混沌DESAPSO算法二維航跡

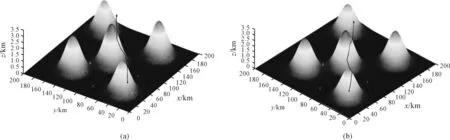
圖3 PSO和混沌DESAPSO算法三維航跡

4 結(jié)論

本文針對(duì)將PSO算法運(yùn)用于無(wú)人機(jī)三維航跡規(guī)劃時(shí)易陷入局部最優(yōu)，導(dǎo)致航跡規(guī)劃品質(zhì)不高的問(wèn)題，提出將DE算法、SA算法嵌入到PSO算法中，并對(duì)PSO算法參數(shù)進(jìn)行混沌優(yōu)化以增加后期種群多樣性，從而利用三種算法各自優(yōu)點(diǎn)提高航跡規(guī)劃品質(zhì)。仿真結(jié)果表明：混沌DESAPSO算法對(duì)航跡品質(zhì)改進(jìn)效果明顯，獲得了滿意的無(wú)人機(jī)三維航跡。

[1] 于成龍，劉莉，王祝,等.基于物理規(guī)劃的無(wú)人機(jī)多目標(biāo)航跡規(guī)劃[J].電光與控制,2015,21(5):1-5.

[2] 王俊，周樹道，朱國(guó)濤,等.無(wú)人機(jī)航跡規(guī)劃常用算法[J].火力與指揮控制,2012,37(8):5-8.

[3] KENNEDY J，EBERHART R C.Particle Swarm Optimization[C]//Proceedings of the 1995 IEEE International Conference on Neural Networks,1995:1942-1948.

[4] 方勝良，余莉，汪亞夫.基于粒子群算法的無(wú)人機(jī)航跡規(guī)劃[J].計(jì)算機(jī)仿真,2010,27(8):41-43.

[5] 陳琳，白振興.應(yīng)用PSO算法的無(wú)人機(jī)三維航跡規(guī)劃[J].電光與控制,2008,15(4):50-53.

[6] 丁偉峰，汲萬(wàn)峰，嚴(yán)建鋼，等.基于種群多樣性測(cè)度的PSO算法及其應(yīng)用研究[J].現(xiàn)代防御技術(shù),2012,40(4):143-149.

[7] 王緒芝.不確定環(huán)境下無(wú)人機(jī)航跡動(dòng)態(tài)規(guī)劃及仿真研究[D].南京:南京航空航天大學(xué),2013.

[8] 胡中華.基于智能優(yōu)化算法的無(wú)人機(jī)航跡規(guī)劃若干關(guān)鍵技術(shù)研究[D].南京:南京航空航天大學(xué),2011.

[9] 劉建平.基于混沌和差分進(jìn)化的混合粒子群優(yōu)化算法[J].計(jì)算機(jī)仿真,2012,29(2):208-211.

[10]楊曉龍，曲東才.一種基于遺傳模擬退火算法的航跡優(yōu)化方法[J].四川兵工學(xué)報(bào),2013,34(12):66-70.

[11]彭志紅，孫琳，陳杰.基于改進(jìn)差分進(jìn)化算法的無(wú)人機(jī)在線低空突防航跡規(guī)劃[J].北京科技大學(xué)學(xué)報(bào),2012,34(1):96-101.

(責(zé)任編輯 楊繼森)

3-D Route Planning of UAV Based on Chaotic DESAPSO Algorithm

TANG Hui-yu, PENG Shi-rui, SUN Jing-jiao, LIU Xiang-lan

(Air Force Early Warning Academy, Wuhan 430019，China)

Particle Swarm Optimization (PSO) algorithm is easy to fall into local optimum, and being applied to 3-D route planning of UAV will result in poor quality. To solve this problem, the chaotic DESAPSO algorithm was put forward by embedding the differential evolution (DE) algorithm and the simulated annealing (SA) algorithm in the chaotic PSO algorithm. The quality of the route was improved from three aspects, the first is to increase diversity of the population by using variation, crossover and competitive selection of DE algorithm; and the second is to jump local optimum by using the probabilistic jumping ability of SA algorithm; and the third is to increase diversity of the population further by chaotic optimization in the parameters of PSO algorithm. The results of simulation show that the quality of route was obvious improved by the chaotic DESAPSO algorithm, and the 3-D route was satisfied.

chaotic particle swarm optimization；differential evolution; simulated annealing; UAV； route planning

2016-08-14；

2016-09-20

唐匯禹(1991—)，男，碩士研究生，主要從事信息與通信工程研究。

10.11809/scbgxb2017.02.021

唐匯禹，彭世蕤，孫經(jīng)蛟，等.基于混沌DESAPSO算法的無(wú)人機(jī)三維航跡規(guī)劃[J].兵器裝備工程學(xué)報(bào)，2017(2):92-96.

format:TANG Hui-yu, PENG Shi-rui, SUN Jing-jiao, et al.3-D Route Planning of UAV Based on Chaotic DESAPSO Algorithm[J].Journal of Ordnance Equipment Engineering,2017(2):92-96.

TP301.6

A

2096-2304(2017)02-0092-05