基于APSO算法的水工弧形閘門主框架優化設計

鄭圣義，陳 笙，姚 輝，董繼富

(1.河海大學能源與電氣學院，江蘇 南京 210098;2.浙江廣川工程咨詢有限公司，浙江 杭州 310020)

0 引言

水工弧形閘門屬于水工建筑物中重要的組成部分，具有極強的空間受力特性，其結構以及受力狀況相對復雜。弧形閘門重量的60%到70%由其主框架構成，其中包括主橫梁，支臂以及面板。影響水工弧形鋼閘門造價和安全性的控制變量較多，以往的設計是憑經驗根據已有條件先擬定各構件尺寸，然后進行強度、剛度和穩定性等約束條件校核，再進行重復驗算，這種方法忽略了弧形閘門結構的整體性，設計出的結構可能某些尺寸取值太過保守，而某些尺寸預留的安全裕度不足，從而造成整個弧形閘門的安全性較低且耗時耗力［1］。其在結構設計過程中，設計者依賴其以往經驗所選出的方案一般并不是最優方案。

目前，國內普遍使用遺傳算法對水工鋼結構進行優化，蔡元奇運用改進的遺傳算法對某水電站的弧形鋼閘門進行了三維有限元優化設計，練繼建等運用序列二次法對比遺傳算法進行鋼閘門的優化設計［2］。本文使用加速粒子群算法(APSO)，結合工程實例對弧形閘門主框架進行優化設計，同時運用遺傳算法進行對比驗證，取得了一定成果。

1 APSO算法簡介

1.1 粒子群算法簡介

粒子群算法(PSO)，是近年來由J.Kennedy和R.C.Eberhart等開發的一種新的進化算法［3］。

取d維搜索空間中第i個粒子的實時位置和速度分別為 Xi=(xi，1xi，2… xi，d) 和 Vi=(vi，1vi，2vi，d)，當粒子找到個體極值和全局最優解時，粒子根據以下方程調整自己的速度和新的位置

式中，w為慣性權重;c1和c2為正的學習因子;r1和r2為0～1之間均勻分布的隨機常數;pi，j代表粒子本身在迭代后找到的最優位置;pg，j代表整個種群內粒子群目前在迭代之后找到的最優位置。

1.2 APSO算法粒子加速系數

粒子群算法的控制參數決定了算法的性能，其中包括學習因子、粒子數、慣性權重等一系列參數。標準粒子群算法(PSO)在運行的早期收斂速度較快，但在后期極易陷入局部最優解，出現早熟收斂［4］。本文使用的APSO算法能解決PSO算法中過早收斂的問題，選取合適的加速系數能夠提高所得解的精確性［5］。加速系數取值如下

式中，λ與最優解有關

式中，ω和φ表示權重系數;ε表示壓縮因子;favg為粒子解的平均值;fmax為粒子解的最大值;fmin為粒子解的最小值。則式(1)可調整為

根據具體算例，利用有限元軟件ANSYS建立弧形閘門模型并對其進行受力分析。其次，記錄應力

式中，n表示待優化量的數目;k表示約束條件的個數;Xi為優化變量，即不同構件的體積;F(x)為目標函數，表示閘門的耗鋼量;cj為約束上限。

本文主要討論主橫梁式弧形閘門，建模時優化對象取為斜支臂，工字型梁閘門，其支臂和主橫梁截面取為箱形截面，當將兩腹板間間距取為零時，即可表示主橫梁或支臂為“工”字形截面［6］。其主框架荷載以及內力分布如圖1所示。

2 優化問題數學模型

水工弧形鋼閘門優化有多變量、多約束以及非線性的特點，將對目標函數(耗鋼量)起決定作用的離散變量作為設計參數Xi，如圖2所示。

式中，x1表示面板厚度;x2、x3表示主梁上、下翼緣(靠近面板處)厚度;x4表示主梁腹板厚度;x5表示支臂翼緣厚度;x6表示支臂腹板厚度;x7表示主梁腹板高度;x8表示支臂腹板高度;x9、x10表示主梁上、下翼緣外延長度;x11支臂翼緣外延長度;x12主梁腹板間距;x13支臂腹板間距;B1為面板有效值。其初始值取設計空間中的隨機值。

2.1 目標函數

目標函數設定為弧形閘門的主體框架，其中包括主橫梁以及閘門支臂即

式中，G1(x)為主橫梁質量;G2(x)為支臂質量。

根據《水利水電工程鋼閘門設計規范》SL 74-2013規定(以下簡稱《規范》)，當面板與主(次)梁相連接時應考慮面板參與主(次)梁翼緣工作，其有效寬度按規范確定［7］。則目標函數可具體表示為分布集中情況并依此建立數學模型，將結構優化問題轉化為力學數學問題。最后，由此模型結合運籌學中相關規劃方法找出問題的最優解。取設計變量X=［X1，X2，…，Xn］，其數學模型可以表示為

圖1 主框架荷載及內力分布

圖2 主橫梁和支臂斷面

式中，ρ代表鋼材的密度，一般取0.007 85 kg/cm3;R為弧形閘門幾何半徑;B為弧形閘門設計寬度;φ1、φ2為主橫梁、支臂重量增加系數，取1.1～1.2;α0為支臂傾斜角。

2.2 約束條件

本文主要討論的約束條件包括強度約束、剛度約束、穩定性約束和幾何約束。其中對于幾何約束應根據實際工況，選擇合適的設計變量波動范圍來合理量化設計變量，使優化結果符合構造要求。其余約束條件均按《規定》所設計。

2.2.1 強度約束

主閘門支臂處理為偏心受壓構件，需驗算其截面上的正應力以及剪切應力。主梁也應驗算其剪切應力和正應力即

由于主梁支撐處分布著較大的彎矩和剪力，故應驗算腹板與翼緣連接處折算應力

式中，N為截面所受軸向力;M為主梁和支臂的截面彎矩，其中主梁包括跨中處以及支承處截面;A為截面面積;W為截面抗彎矩;［σ］為容許正應力;Q為截面剪力;S*為驗算剪應力處以外的截面對中性軸的面積矩;I為截面對中性軸的慣性矩;t為腹板厚度;［τ］為容許剪應力。

2.2.2 剛度約束

根據《規定》，將主橫梁按簡支梁(兩端有懸臂段)承受均布荷載進行剛度校驗，跨中截面承受最大撓度;對于根據實際情況取支臂長細比λx或λy均不大于120。

式中，q為承受均布荷載;b為主梁跨中長度;c為主梁懸臂梁長度;E為彈性模量;為容許相對撓度。

2.2.3 穩定性約束

支臂整體穩定性:由于主框架具有空間性，因此應分別驗算在平面內、外的主框架支臂穩定性

式中，Φp為平面內彎矩穩定系數;Φ1為平面外彎矩穩定系數。

2.2.4 幾何約束

對設計變量進行控制，使其構成滿足限制條件的設計空間。

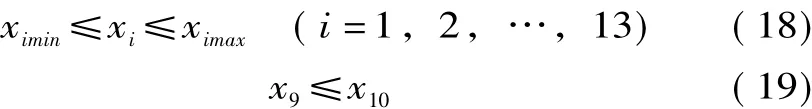
式中，ximin和xmax分別表示xi的上限值和下限值。

2.3 約束問題的處理

本文研究的優化問題設計變量多，且約束條件多為隱式約束，目標函數為有約束優化。粒子群算法主要研究無約束問題，因此采取懲罰函數法使目標函數變為無約束優化問題［8］。即將目標函數調整為適應度函數

式中，F(x，M)為懲罰函數;M為懲罰因子，是一個充分大的正數;g(x)為優化問題的不等式約束條件。

3 工程算例

某工程溢流壩露頂式斜支臂弧形閘門，布置方式為主橫梁式。門寬14.0 m，門高13.152 m，設計水頭13.152 m，弧門半徑16 m，支鉸高度22.0 m。該閘門選用16 Mn鋼，彈性模量E=206 GPa，泊松比μ=0.3。該閘門支臂以及主橫梁為工字型梁，因此取腹板間隔為0，設計變量減為11個。對優化前弧形閘門模型進行建模分析，其ANSYS模型如圖3所示。其主橫梁最大折算應力為97 MPa，出現于上主橫梁跨中界面處。

表1 各設計變量優化前后對比cm

圖3 閘門有限元計算模型

對設計變量采取二進制編碼，迭代次數選取100次，gama參數設置為0.95。引入遺傳算法進行對比驗證，約束條件及處理方法同上。加速粒子群算法其經過20次迭代得出最優解，遺傳算法經過約30代得出最優解，優化結果如表1、表2所示。將APSO算法優化結果進行整體建模，其主橫梁折算應力圖如圖4所示，其最大折算應力為116 MPa小于容許應力［σzh］=165 MPa，處于容許范圍內。結果表明，利用APSO算法對弧形閘門的優化是成功的，它成功地減輕了主框架整體重量，節約了工程投資。兩種方法對各變量優化結果以及速度不同，原因是兩者尋優思想不同，粒子群算法每個粒子的位置更新都直接與位置最佳的的粒子相關，得出的最優個體的各個參數會直接映射于種群中的其他個體，而遺傳算法對于優良的個體的處理則是概率性的保留，這也造成了在求解單峰問題時遺傳優化算法的收斂速度以及求解精度均低于粒子群優化算法。

表2 優化結果對比

圖4 主橫梁折算應力(單位:MPa)

4 結論

本文采用加速粒子群算法(APSO)對閘門框架進行優化設計，并對比遺傳算法加以驗證，在弧形閘門框架優化方面取得了顯著地成果。使用APSO算法優化各項參數，閘門總重減輕13.3%，且最大折算應力處于安全范圍，其優化結果優于常用的遺傳算法。上述優化設計基于靜力對結構的作用，為同類型結構受力優化提供了嶄新的思路和對比驗證。

［1］蔡元奇，彭波，朱以文，等．基于ANSYS的遺傳算法在水工弧形鋼閘門優化設計中的應用［J］．武漢大學學報:工學版，2005，38(5):50-53．

［2］練繼健，李火坤．基于SQP算法的露頂式弧形閘門主框架優化設計［J］．水利水電技術，2004，35(9):63-66．

［3］FARKAS J， JRMAI K．Optimum Design of Steel Structures［M］．Springer Verlag，2013:19-23．

［4］劉衍民，牛奔．新型粒子群算法理論與實踐［M］．北京:科學出版社，2013．

［5］AGRAWAL J， AGRAWAL S．Acceleration based Particle Swarm Optimization(APSO)for RNA Secondary Structure Prediction［C］∥Progress in Systems Engineering，2015:741-746．

［6］李宗利，何運林．弧形閘門主框架優化設計［J］．西北水資源與水工程，1993，4(4):35-40．

［7］SL 74—2013 水利水電工程鋼閘門設計規范［S］．

［8］余勝威．MATLAB優化算法案例分析與應用［M］．北京:清華大學出版社，2014．