基于高頻波動率的銅鋁期貨動態關聯性研究

朱學紅　陳強　諶金宇

內容提要：基于高頻數據的時變跳躍性，本文選取2010-2015年上海期貨交易所銅鋁期貨一分鐘收盤價作為樣本數據，將銅鋁期貨高頻數據的已實現方差（RV）分解為連續樣本路徑方差（CV）和離散跳躍方差（JV），并運用DCC-MVGARCH模型分別計算連續樣本路徑方差和離散跳躍方差之間的動態相關系數。結果表明，銅鋁期貨高頻波動率之間存在明顯的正相關性，銅鋁期貨連續變差的相關性與跳躍變差的相關性在動態路徑上存在顯著性差異，并且前者的相關性程度要高于后者；受歐債危機等極端事件的影響，連續變差與跳躍變差的動態相關性均呈現出局部的高點。

關鍵詞：跳躍；已實現方差；期貨市場；動態相關性；高頻數據

中圖分類號：F83093 文獻標識碼：A 文章編號：1001-148X（2017）02-0050-08

一、引言

不同金融市場波動率的相關性分析，在金融資產配置、金融風險管理以及投資組合策略的選擇等方面都有著非常廣泛的應用。有色金屬是我國最早進入期貨市場的行業，也是運行最為成熟、市場化和國際化程度最高的代表性行業[1]，歷經近20年的發展，我國有色金屬期貨市場已成為金屬交易量僅次于倫敦金屬交易所（LME）的重要金屬期貨交易場所。近年來，隨著我國金屬期貨市場的不斷完善，加之商品指數基金、高頻交易策略以及電子信息技術的不斷發展，金屬期貨的金融屬性不斷凸顯，越來越多的投資者進入金屬期貨市場，通過配置不同品種的投資標的，在同樣風險程度上獲得更高的回報。因此，不同金屬期貨品種的相關性研究有助于投資者將其投資組合有效的拓展到更具有獲利能力和風險分散能力的特定金屬期貨市場當中去，同時也有助于揭示我國金屬期貨市場的風險特質以及為政府監管政策制定提供理論參考。

相關性是多變量金融時間序列研究的重點，資產分配和風險管理都依賴于相關性。目前對不同期貨品種波動率的相關性研究的方法主要是基于GARCH族模型。如Hany（2003）等[2]構建了GARCH模型來考察紐約商品期貨交易所電力期貨與現貨之間的相關關系，發現電力期貨與現貨之間不僅存在簡單的靜態相關關系；Liu和An（2011）[3]則采用M-GARCH模型研究了中國銅期貨市場、銅現貨市場與美國銅期貨市場之間的信息傳導機制，顯示中美市場之間存在雙向波動溢出效應，但是美國銅期貨市場在市場聯動中發揮的作用更大；Saban等（2013）[4]研究了石油與四種農產品小麥、玉米、大豆和糖的波動溢出效應，結果發現只有在金融危機前石油價格引導農產品市場。Joschat和Robert（2014）[5]運用GARCH-in-mean VAR 模型對玉米、棉花和小麥等農產品期貨市場價格之間的波動溢出效應進行了研究，研究發現，在短期內不同品種農產品期貨市場價格之間存在波動溢出效應，玉米期貨市場對小麥和棉花期貨市場均存在顯著的波動溢出效應；Perry（2014）[6]采用VARMA-AGARCH 和DCC-AGARCH 模型研究新興市場銅、石油和小麥的波動性和動態相關性，結果顯示，這些商品的相關性在2008年后呈增強趨勢；Brenda和Franziska（2016）[7]研究了德國能源價格和農產品價格的波動溢出關系和動態關系，結果并沒有發現能源價格影響農產品價格波動的證據。

但是以往的研究大多是建立在日度數據或者是更加低頻的數據之上的，對于高頻數據或者是超高頻數據的研究卻很少涉及。近年來，日內高頻交易數據的可獲得性為金融波動率的研究提供了新的方向。Andersen等（2001）[8]、Barndorff-Nielsen和Shephard（2002）[9]等提出以日內高頻收益平方和計算的“已實現波動（Realized Volatility，RV）”作為真實波動率的估計量，從而使金融波動率由隱變量預測轉變為可以直接建模刻畫的顯變量。一些國內學者對高頻數據也有所研究，比如郭名媛和張世英（2009）[10]他們在原有的已實現波動率的模型上加入了賦權已實現波動率和賦權已實現協方差估計量來研究滬深股市高頻數據之間的相關性，并且加入了Bayes來檢測變結構點。徐正國和張世英（2006）[11]建立了高頻數據之間的FIVAR模型刻畫了上證指數跟深圳成指之間的相關性模型。汪東華和索園園（2014）[12]采用降趨交叉相關分析方法和多重分形降趨交叉分析方法分析了滬深200股指期貨跟現貨1分鐘高頻數據之間的相關性，發現隨著市場波動程度加大，市場之間的交叉相關性增強。周偉和何建敏（2015）[13]考慮時變因素研究金融風險傳染效應，發現結合時變測度模型來分析金融市場的高頻數據是一種有效的方法。上述研究主要針對股票市場，對于金屬期貨市場的高頻波動率的研究確很少，并且主要考察的是連續變差之間的相關性；但是許多學者發現，在日內近似連續的時間內金融資產的收益率有可能會出現大幅波動，這種現象稱為“跳躍”（jump），其在金融資產收益波動率的估計和預測中具有非常重要的意義。基于Barndorff-Nielsen和Shephard（2006）[14]二次冪變差測量的理論結果，Andersen等（2007）[15]以及Corsi和Reno（2012）[16]先后將已實現波動率分解為連續樣本路徑方差和離散跳躍方差，它們的研究結果均表明將連續變差和跳變差分離之后的模型比未分離的模型具有更好的模擬效果。

鑒于上述文獻研究的不足，本文依據Andersen等（2001）[8]的研究成果，以期銅和期鋁為研究對象，將高頻已實現波動率分解為連續樣本路徑方差和離散跳躍方差兩部分，然后運用DCC-MVGARCH模型分別計算連續樣本路徑方差和離散跳躍方差之間的動態相關系數，并且與沒有進行分解的已實現方差波動率相關系數進行比較。本文的主要貢獻在于：首先，以往的研究大多集中于股票市場及股指期貨市場的研究，針對商品期貨尤其是有色金屬期貨市場的研究非常少見，而有色金屬在中國產業結構和國民經濟中的有著至關重要的地位，因此針對我國有色金屬期貨市場量價關系的研究具有重要意義；其次，國內對不同期貨品種波動率相關性的研究主要通過對收益條件方差建模間接刻畫，較少將金融波動率由隱變量轉變為可以直接建模刻畫的顯變量，尤其是將已實現波動率進一步分解為連續波動與跳躍波動，從考慮跳躍的角度去探討相關性的相關研究就更少；最后，國內相關研究多基于日度數據，基于高頻數據的研究較少，而Avramov等（2006）[17]的研究發現，使用高頻數據比使用日度數據有超過兩倍的解釋能力，因此基于高頻數據的研究可顯著提升實證結果的可信度。

二、基于高頻數據的跳變差分解模型

（一）已實現波動率的度量

高頻數據的波動率的真實度量用已實現波動率（RV）來表示（Andersen和Bollerslev，1998）[18]將已實現波動率定義為日內高頻收益率的平方和，將每個交易日分為M個時間段，第t個交易日第j個時間段的收益率記為：

rt，j=Ln（pt，j/M）-Ln（pt，（j-1）/M）

（j=1，2，3，…，M）（1）

則第t個交易日的已實現波動率可以表示為：

RVt（M）=∑Mj=1r2t，j（2）

近年來的理論和實證研究均表明金融資產價格并不一定是連續的，金融資產價格運行過程中普遍存在跳躍。一般假設交易時間內金融資產價格p（τ）變化服從跳躍—擴散過程：

dp（τ）=μ（τ）dt+σ（τ）dW（τ）+k（τ）dq（τ）（3）

其中μ（τ）為連續的局部有限變動的漂移系數，σ（τ）>0為隨機波動率過程，W（τ）為標準布朗運動，q（τ）是泊松跳躍過程，λ（τ）為跳躍強度，k（τ）dq（τ）表示純跳躍部分。如果資產價格在τ時刻無跳躍，那么dq（τ）=0，否則，dq（τ）=1；k（τ）為跳躍的幅度。跳躍的幅度k（τ）和頻率λ（τ）均為時變的。

基于以上假設，將二次變差分解為跳躍所帶來的非連續變差Jt和隨機波動所組成的連續變差Ct兩部分，收益率從τ到τ+1的二次變差可以表示為：

QVt=∫tt-1σ2（τ）dτ+∑Ntj=1k2t，j（4）

其中等式右邊第一部分是由價格過程的連續部分形成的積分方差（Integrated variance，IV），也叫連續變差部分Ct，表示連續部分對已實現波動率的貢獻；右邊第二部分是由價格過程的跳躍部分所形成的跳變差部分Jt，表示跳躍部分對已實現波動率的貢獻，其中Nt表示在第t日跳躍發生的次數，kt，j表示第t日第j個跳躍的幅度。

根據Barndorff-Nielsen & Shephard（2002）[19]的研究，若資產價格過程不存在跳躍，當取樣頻率趨于無窮大時，已實現波動率是積分方差的一致估計；若資產價格過程存在跳躍時，已實現波動率依概率收斂于二次變差過程，即

（二）跳躍檢驗統計量以及連續變差和跳變差的分離

由于采用Barndorff-Nielsen和Shephard[14]所提出的已實現雙冪次變差（Realized BipowerVariation，RBV）的計算受日內抽樣頻率的影響很大，主要表現在隨著抽象頻率的提高，RBV估計量會因為受到市場微觀結構等因素的影響而不能收斂到幾分波動率，因此采用RBV作為到離散跳躍方差檢驗的穩健估計量是有偏差的。考慮到高頻數據特有的“日歷效應”，于是本文采用Andersen等（2012）[20]提出的一種全新的估計量已實現中位數波動率MedRVt代替傳統的已實現二次冪變差以及相應的跳檢驗統計量（Zt），將已實現波動率中的連續變差部分Ct和跳躍引起的非連續變差部分Jt分離。

在價格過程是半鞅（Semi-Martingale）加有限跳躍過程的假設下，已實現中位數波動率（MedRVt）依概率收斂于積分方差（IV）：

結合式子（3）和（7）可以得出，已實現波動率RVt（M）和已實現中位數波動率MedRVt（M）之差依概率收斂于二次變差過程中由跳躍形成的部分：

因此，在不存在跳躍時，已實現波動率與已實現中位數波動率的差為0。即在考慮跳躍過程的情況下，已實現波動率的收斂結果不只受到積分方差的影響，同時也受到跳躍方差的影響。

本文采用Huang和Tauchen（2005）[21]所提出的近似服從正態分布的跳檢驗統計量Zt檢驗跳躍的存在性：

通過比較Zt與標準正態分布在顯著性水平α對應的臨界值的大小，就可以判斷跳躍波動率是否存在。基于跳檢驗統計量Zt，二次變差中的跳變差部分Jt可以用下式進行度量：

Jt=I（Zt>Φα）·（RVt-MedRVtt）（11）

其中I（·）為示性函數，標準正態分布在顯著性水平α對應的臨界值為Φα，借鑒已有研究經驗，本文選取α=099。這一定義實現了已實現波動率連續部分和跳躍部分的

非參數度量。相應的，二次變差中的連續部分的度量可以表示為：

Ct=I（ZtΦα）·RVt+I（Zt>Φα）·MedRVt（12）

（三）考慮跳躍的銅和鋁期貨各部分波動率之間動態相關性分析

以前的一些相關性的GARCH族模型在參數估計和經濟意義的解釋等反面都存在一些缺陷，而Engle（2002）[22]提出的DCC-MVGARCH模型具有穩定性、直觀性、簡潔性等特性，并且在對大規模的數據樣本的動態相關系數的計算方面有獨特的優勢。DCC-MVGARCH又叫“動態相關系數多元GARCH模型”，也是非常成熟的模型，國內外許多學者都對它進行了一些研究。所以本文選用DCC-MVGARCH作為實證基礎，將條件協方差方差矩陣Ht定義為：

三、實證分析

（一）數據選取與處理

本文以我國兩種最典型的有色金屬期貨品種——期銅和期鋁為例，選取上海期貨交易所3個月到期的銅鋁期貨的1分鐘收盤價高頻數據為研究對象進行實證分析。樣本區間選取2010年7月1日至2015年12月31日（除去節假日，共計1 338個交易日），樣本區間內上海期貨交易所的交易時間為上午8：59到11：29以及下午13：30到15：00，每天共計227個時間間隔，即M=227。數據來源于國泰安數據庫（CSMAR），該數據庫主要是參照COMPUTERSTAT和CRSP等大型國際數據庫開發而成，它是全國涵蓋中國金融、經濟等主要領域的高精準研究型數據庫，其主要包括了股票市場、公司研究、行業研究、債券市場、衍生市場、經濟研究、基金市場、專題研究和海外研究等、共59個數據庫，其開發理念主要是為了滿足不同用戶的需求，幫助用戶更快捷、更方便的構建研究模型。以下將對樣本數據選取和描述性統計及實證的結果進行分析。

（二）銅和鋁期貨各部分波動率描述性統計分析

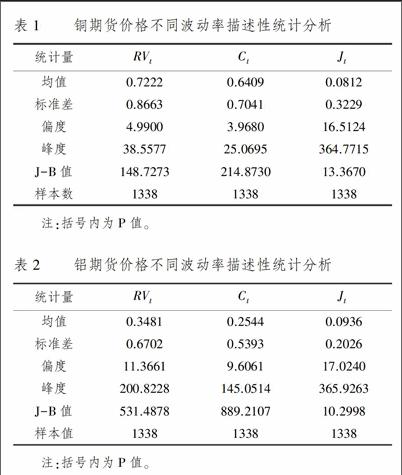
將銅鋁期貨已實現波動率RVt分解為連續變差（Ct）部分和跳變差部分（Jt）。然后分別對得到的已實現波動率RVt，連續變差（Ct）部分和跳變差部分（Jt）進行一般的描述性統計分析，結果如表1和表2所示。

表1和表2分別報告了銅期貨和鋁期貨波動率各組成部分的描述性統計量。從均值來看，銅期貨連續和跳躍部分的均值分別為06409和00812，鋁期貨的連續和跳躍部分的均值分別為02544和00934，銅和鋁期貨的連續變差的均值均大于跳躍變差的均值，這說明連續變動部分是日波動率最主要的組成部分，由跳躍引起的波動比例較小，但也是很重要的一部分，不可忽略。從標準差來看，銅期貨的連續和跳躍部分的標準差分別為07041和00812，鋁期貨的連續和跳躍部分的標準差分別為05393和02026，金屬期貨的連續變差大于跳躍變差，并且期銅價格的標準差高于期鋁，說明期銅的價格波動比期鋁大，這也正好對應目前SHEF市場金屬期貨中滬銅最為活躍及其流動性、交易量均較大成熟較高度的實際情況，也是需要進一步加強滬鋁市場建設的現實原因。從偏度來看，各序列均為右偏，銅鋁期貨已實現波動率及其分解量序列的偏度和峰度表明價格波動具有顯著的尖峰厚尾特征，期銅和期鋁的已實現波動率序列及其分解量序列均不服從正態分布。其中Ljung-Box Q統計量揭示了序列的自相關性，銅期貨和鋁期貨的連續變差序列Ct都很大，這說明銅期貨和鋁期貨的連續變差序列均具有很強的自相關性，這一點從圖形上也可以得到印證；而銅期貨和鋁期貨的跳變差序列Jt的自相關性都很弱，這樣就不利于直接對其進行建模和預測。

（三）期銅跟期鋁各部分波動率分析

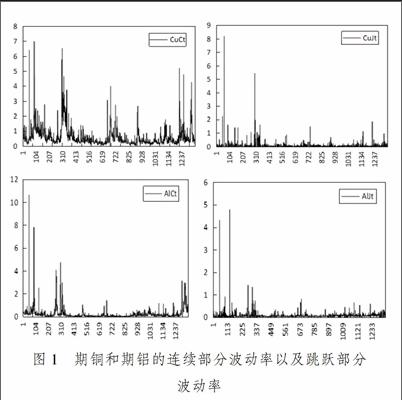
本部分主要是銅和鋁期貨的連續部分方差和跳躍部分方差的波動率，依次代表銅期貨的連續部分方差波動率、銅期貨跳躍部分方差波動率、鋁連續部分方差波動率、鋁跳躍部分方差波動率。

圖1 期銅和期鋁的連續部分波動率以及跳躍部分

波動率

圖1銅跟鋁的連續部分和跳躍部分的波動率可以看出前期的波動率的幅度明顯的大于后期的波動率，并且銅期貨的波動率也要強于鋁期貨的波動率。近年來很多學者對跳躍的頻率的頻繁程度進行了研究，并且都發現了跳躍是具有集聚性的。經統計顯示，在選定的樣本區間和置信水平下，在總樣本數1 338下，使用MedRV估計量來計算跳躍發生的天數時，銅期貨發生跳躍的天數有588天，鋁期貨發生跳躍的天數有546天，所以期銅和期鋁分別對應的發生跳躍的頻率為4394%，4080%，可見銅和鋁期貨發生跳躍也是和股票市場一樣非常頻繁的，但是還是略低于相同統計量下的股票市場的跳躍的頻率。期銅和期鋁各部分的波動率都圍繞各自的均值上下波動，可以發現序列波動存在很大的集群性，正如波動聚集現象一樣，跳躍方差波動率也會出現聚集現象，比如在某些時段，跳躍次數會增多，跳躍的幅度也會隨之放大。從各部分的波動率的走勢及波動程度不難看出可以認為波動存在ARCH效應。另外可以很明顯地看出期鋁價格的波動頻率和幅度明顯的低于期銅價格的波動頻率和幅度，這表明我國的期銅的投資者和參與者多于期鋁的投資者及參與者，這也恰恰說明我國期鋁市場比期銅市場要更加的脆弱，所以在考慮期銅跟期鋁的相關性的時候區分考慮離散跳躍方差和連續樣本路徑方差也是十分有必要的。

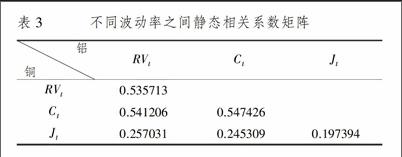
（四）期銅跟期鋁各部分之間靜態相關系數分析

根據一般的自相關公式得出自相關矩陣表3列出了銅和鋁各部分統計量之間的相關系數圖2。從圖中可以明顯看出連續部分的相關系數可以明顯的強于跳躍部分的相關系數，從表中不難看出期銅跟期鋁各部分之間的相關系數都是在-1到1之間，并且期銅跟期鋁之間的系數都是大于1，說明期銅跟期鋁之間是呈現出正相關的關系，銅鋁期貨市場之間存在“齊漲齊跌”的現象；從表3看出期銅與期鋁之間已實現波動率的價格波動相關系數比較高（05左右），期銅和期鋁連續部分的價格波動相關系數也在05之間，但是跳躍部分的價格波動之間的相關系數就相對比較低，在01之間。可以看出期銅與期鋁的價格指數的波動率跟分解出來的連續部分的已實現波動率之間的相關系數差不多，只是連續部分的相關系數較未分解的時候大，從這里就充分的可以得出日的已實現波動率不僅僅是受到連續部分的影響，可能還受到跳躍部分的影響。當然跳躍也分很多的滯后的因素，滯后階數的不同也可能從很大程度上面影響實驗的結果。

（五）期銅跟期鋁動態相關系數分析

經DCC-MVGARCH模型估計的時變相關系數結果如圖2至圖4所示。首先看未分解的銅鋁期貨已實現波動率的動態相關系數，從圖2并結合表4的描述性統計可以看出，兩者的相關性沒有呈現明確的趨勢，并且波動幅度較大，在-011297和0983之間波動；在2013年呈現兩個局部低點，相關性系數落到0以下，此時有利于將銅鋁期貨納入投資組合，實現風險最小化。進一步將已實現波動率分解為連續變差與跳躍變差，分別考察銅鋁期貨連續變差的相關性與跳躍變差的相關性，可以看出，兩者的動態相關性呈現出與已實現波動率不一樣的軌跡，這表明若沒有將連續變差和跳躍變差剝離，所得研究結論在市場投資、政策建議方面極可能產生誤導作用，因為現實中連續性和跳躍性波動二者是同時存在，并且共同發=產生作用。從圖3可以看出，銅鋁期貨連續變差的動態相關性呈現出先下降后上升的趨勢，相關系數在整個樣本期內都在02以上，均值為03829，在2010年下半年，相關系數在達到局部最大值07832后逐步呈現下降趨勢，并在2014年末開始反彈逐漸上升，維持在04左右；從標準差來看，其值為0122257，表現出較大的波動性，甚至大于未分解的已實現波動率的標準差。

而從銅鋁期貨跳躍變差的動態相關性來看，前期波動較大，在2010年8月從03下落到0以下，之后迅速上升，并在2010年11月達到局部最大值09136后迅速下降到02左右，之后有所上升并從2011年初開始，一直維持在03左右，并且波動幅度也較小，跳躍變差的相關性主要反映極端市場變動導致的市場聯動變化。從銅鋁期貨的跳躍變差相關性來看，主要在2010年下半年波動較大，并且在短期內大幅增強又迅速下降，這主要是2010年下半年正是歐債危機發酵的時刻，使得銅鋁期貨市場之間的傳染效應大大增強，提高了兩者的相關性。從連續變差的動態相關系數來看，其也受到歐債危機的顯著影響，根據金融危機傳染理論，由于信息約束下的投資者羊群效應，極端情況下收入效應的增加，投機行為增多，導致了賣壓的增強以及市場流動性的降低，而流動性的降低進一步加劇了價格下降，這種趨同的賣出行為就使得地區之間的價格走勢更加一致，表現為銅鋁期貨市場相關性的增加，可見，動態相關性指標更能明確地反映出金融危機時期的市場特征。

四、結束語

本文依據Andersen等[18]的研究成果，采用1分鐘高頻數據，對我國銅鋁期貨市場高頻波動率的相關性進行了考察，通過分離銅鋁期貨已實現波動率的連續波動成分和跳躍成分，然后運用DCC-MVGARCH模型分別計算連續樣本路徑方差和離散跳躍方差之間的動態相關系數，得出以下結論：

（1）期銅跟期鋁價格波動之間存在明顯的正相關性，即銅鋁期貨市場之間存在“齊漲齊跌”的現象。受全球經濟宏觀形勢以及金融投機影響，我國有色金屬期貨市場價格波動劇烈，因此有色金屬期貨市場上的監管者在關注市場動向、分析價格波動、進行政策制定時，可以依據銅鋁價格波動之間的相關性大小，重點監測某一金屬品種，判別另一金屬品種的風險，降低監管成本。

（2）銅鋁期貨連續變差的相關性與跳躍變差的相關性在動態路徑上存在顯著性差異，并且前者的相關性程度與波動幅度要高于后者。因此，準確把握銅鋁期貨跳躍變差相關性，能夠有效地降低極端市場變動導致的損失，滿足資產多樣化的要求；同時對監管機構而言，可以依據連續變差與跳躍變差相關性的動態路徑差異，有針對性建立相應的跨市場監管機制。

（3）銅鋁期貨連續變差的動態相關系數和跳躍變差的動態相關系數都在2010年呈現出局部的高點。說明在歐債危機等極端事件的影響下，銅鋁期貨市場的相關性有局部的上升，這可能源自于投機環境下賣壓的相互傳染。因此，針對金融市場的風險監管不僅要考慮市場內部的隨機因素，還需要兼顧市場外的傳染因素，尤其要對外部極端事件的影響予以充分重視。

參考文獻：

[1] 蔣曉全.我國有色金屬產業發展與期貨市場[J].世界有色金屬，2012（10）：72-73.

[2] Hany A.Shawky，Achla Marathe. A first look at the empirical relation between spot and futures electricity prices in the united states[J].The Journal of Futures Markets，2003，23（10）：931-955.

[3] Liu，Q F，An Y B.Information transmission in informationally linked market：Evidence from US and Chinese commodity futures market[J].Journal of International Money and Finance，2011，30（5）：778-795.

[4] Saban Nazlioglu，Cumhur Erdem，Ugur Soytas.Volatility spillover between oil and agricultural commodity markets[J].Energy Economics，2013，36（3）：658-665.

[5] Joscha Beckmann，Robert Czudaj.Volatility transmission in agricultural futures markets[J]. Economic Modelling，2014，36（1）：541 -546.

[6] Perry Sadorsky.Modeling volatility and correlations between emerging market stock prices and the prices of copper，oil and wheat[J].Energy Economics，2014，43（5）：72-81.

[7] Brenda López Cabrera，Franziska Schulz.Volatility linkages between energy and agricultural commodity prices[J].Energy Economics，2016，54（2）：190-203.

[8] Andersen T G，Bollerslev T，Diebold F X，et al. The distribution of realized stock return volatility [J]. Journal of Financial Economics，2001，61（1）：43-76.

[9] Barndorff-Nielsen O E，Shephard N. Estimating quadratic variation using realized variance [J]. Journal of Applied Econometrics，2002，17（5）：457-477.

[10]郭名媛，張世英. 基于高頻數據的滬深股票市場的相關性研究[J]. 系統工程學報，2009（3）：293-298.

[11]徐正國，張世英. 多維高頻數據的“已實現”波動建模研究[J]. 系統工程學報，2006，21（1）：6-11

[12]汪冬華，索園園. 我國滬深300股指期貨和現貨市場的交叉相關性及其風險[J]. 系統工程理論與實踐，2014（3）：631-639.

[13]周偉，何建敏. 考慮時變與高頻因素的金融風險傳染效應分析——以SHFE市場金屬期貨為例[J]. 數理統計與管理，2015（3）：540-549.

[14]Barndorff-Nielsen O E，Shephard N. Econometrics of testing for jumps in financial economic using nipower variation [J]. Society for Financial Econometrics，2006，4（1）：1-30.

[15]AndersenT G，Bollerslev T，Diebold F X. Roughing it up：including jump components in the measurement，modeling，and forecasting of return volatility[J]. Review of Economics and Statistics，2007，89（4）：701-720.

[16]Corsi F，Reno R. Discrete-time volatility forecasting with persistent leverage effect and the link with continuous-time volatility modeling [J]. Journal of Business & Economic Statistics，2012，30（3）：368-380.

[17]Avramov D，Chordia T，Goyal A. The impact of trades on daily volatility[J]. Review of Financial Studies，2006，19（4）：1241-1277.

[18]Andersen T G，Bollerslev T.Answering the skeptics：Yes，Standard volatility models do provide accurate forecasts[J].International Economic Review，1998，39（4）：885-905.

[19]Barndorff-Nielsen O E，Shephard N.Econometric analysis of realized volatility ant its use in estimating stochastic volatility models[J].Journal of the Royal Statistical Society（Series B），2002，64（2）：253-280.

[20]Andersen T G，Dobrev D，Schaumburg E. Jump-robust volatility estimation using nearest neighbor truncation[J]. Journal of Econometrics，2012，169（1）：75-93

[21]Huang Xin，Tauchen G. The relative contribution of jumps to total price variance [J]. Journal of Financial Econometrics，2005，3（4）：456-499.

[22]Engle.Dynamic conditional correlation：a simple class of multivariate generalized autoregressive conditional heteroskedasticity models[J].Journal of Business andEconomic Statistics，2002，20：339-350.

Dynamic Relevance between Copper and Aluminum Futures based on

High-frequency Volatility

ZHU Xue-hong1，2，CHEN Qiang1， CHEN Jin-yu1

（1.School of Business， Central South Universtiy， Changsha 410083，China；

2. Institute of Metal Resources Strategy， Central South Universtiy， Changsha 410083， China）

Abstract：Based on the time-varying jump of high-frequency data， the one-minute closing price of copper-aluminum futures in Shanghai Futures Exchange from 2010 to 2015 is selected as sample data， and the realized variance （RV） of copper-aluminum futures high-frequency data is decomposed into continuous sample path variance （CV） and discrete jump variance （JV）. The DCC-MVGARCH model is used to calculate the dynamic correlation coefficients between the continuous sample path variance and the discrete jump variance. The results show that there is an obvious positive correlation between the volatility of copper and aluminum futures， the correlation between CV and JV is significantly different in dynamic path， and the former correlation degree is much higher than the latter； under the shock of extreme events such as the European debt crisis， the dynamic correlation between CV and JV reaches to a high point to some extent.

Key words：jump； realized variance； futures market； dynamic correlation； high-frequency data

（責任編輯：嚴元）