基于突變理論的北京市水資源安全分析

謝開杰，李繼清

(華北電力大學 可再生能源學院，北京 102206)

0 引 言

水資源是人類社會賴以生存和發展的重要物質資源。隨著人口增長和社會經濟不斷發展，水資源短缺形勢越發嚴峻，水資源安全問題日益成為人類社會關注的焦點問題之一。廣義的水資源安全，是指水資源對國家的可持續發展具有良好的支撐和保障能力[1]。具體到某一區域，則指可供水資源量要滿足其正常發展所必需的水量，又不致產生洪澇災害，社會經濟和生態環境才能維持可持續發展。因此，水資源安全問題研究對區域水資源的合理開發、高效利用和綜合管理具有重要意義。

近年來，很多學者對水資源安全問題進行了不同層次的研究，主要包括水資源安全定義、評價指標體系以及評價模型的建立。酈建強[2]等提出水資源系統的狀態穩定和功能健全是水資源安全的標志，其安全狀況與水資源承載狀況、水環境承載狀況、水生態安全狀況和經濟社會的供水保障狀況有關。Van Leeuwen[3]等通過分析水資源系統特性，提出了水資源壓力指數和水資源安全指數的概念，并基于此建立了水資源安全評價指標體系。賈紹鳳[4]等利用包含水資源狀況、社會、經濟和生態四方面因素的水資源安全評價指標體系，對海河流域水資源安全現狀進行了評價，分析了造成海河流域水資源安全問題的主要原因。Schneider[5]等提出從水資源容量的角度衡量水資源安全，并建立了水資源供需平衡指標來分析流域水資源安全程度。高媛媛[6]等采用改進的層次分析法和基于因子分析的聚類分析法，對福建泉州2008年的水資源安全狀況進行了評價，并分析了2000-2008年泉州市的水資源安全變化趨勢。Lu[7]等采用基于模糊集理論的水安全評價方法對成都的水資源安全形勢進行了評價，計算得到成都市水安全保障指數和水環境壓力指數。

北京是水資源嚴重匱乏的特大城市，近年來，北京地區上游來水量大幅下降，深層地下水資源日益枯竭，然而城市規模擴大、人口增長、社會發展和居民生活水平的不斷提高使得城市用水剛性需求持續增長。保障社會經濟穩定發展和人民生活水平有賴于水資源的支撐，在資源稟賦不佳的情況下進行合理的水資源管理是北京市城市發展的重中之重，因而尋求保障城市發展的水資源安全閾值具有重要意義。本文應用突變理論，建立了北京市水資源安全尖點突變模型，應用突變評價法對模型變量進行量化歸一，得出了保障北京市水資源安全的水量供需差值。同時，利用灰色系統模型對北京市2020年和2030年的需水量進行了預測，并結合北京市近30年來的供水狀況，在特定供水保證率下對北京市2020年和2030年的用水安全狀況進行了評估。

1 水資源安全分析突變模型

1.1 突變理論

突變理論最初由法國數學家Rene Thom創立，是一門研究由漸變引起突變的系統理論。它通過簡潔的數學模型(研究對象的勢函數)研究變化交界處的奇異性態，可用于分析復雜的系統行為。系統的勢函數可以表示系統的任一狀態，不同狀態的取值取決于狀態變量和控制變量的變化。通過研究系統的勢函數，可以直接分析其臨界點附近的不連續特征，使得突變理論尤其適用于研究內部機理尚不明了的系統。

水資源系統安全問題涉及的變量繁多，且安全性評價指標和方法不一，難以客觀評價系統處于穩定連續狀態還是突變狀態；此外，水資源系統危機發生的機理符合突變理論的一般性特征，在水資源系統中，若水資源供需差值不在保障區域穩定發展的合理區間內，則可能會導致其發展狀態的破壞，即發生突變。因此，適宜將突變理論用于水資源安全分析。近年也有不少學者將突變理論用于水資源系統的分析評價當中。孫雪峰[8]等將突變理論應用于水生態系統的分析，建立了水生態系統的尖點突變模型，用于水生態系統狀態的判斷、預警、改善和規劃。李繼清[9]等應用突變評價理論，通過構建長江流域洪災綜合風險評價指標體系，對長江流域1995-2000各年的洪災綜合風險進行了評估。Chen[10]等建立了城市水資源可持續利用水平突變評價模型，并對大連市進行了水資源可持續利用評估。尖點突變模型是常用的、最易被人接受的突變模型，通過構建水資源安全的尖點突變模型，能夠客觀地把握水資源安全狀態與其影響因子之間的響應模式，判斷水資源安全情勢，從而能科學合理地進行水資源管理。

1.2 水資源安全分析尖點突變模型

尖點突變模型的勢函數由一個狀態變量x和兩個控制變量u，v組成，其標準型為：

V(x)=x4+ux2+vx

(1)

式中：x為系統狀態變量；u、v分別為系統的主、次控制變量。

勢函數的臨界點由V′(x)=0決定，該方程的幾何圖形是一個曲面，稱為勢函數的平衡超曲面(如圖1),即：

4x3+2ux+v=0

(2)

對勢函數(1)二次求導，得到奇點方程為：

12x2+2u=0

(3)

聯立式(2)、式(3)消去x得到分歧集方程為：

B=8u3+27v2=0

(4)

通過圖1的平衡超曲面，可以更為直觀地理解突變的機理。平衡超曲面在平面上的投影即分歧集B，超曲面上的點在折疊曲線的邊緣位置發生突跳，隨著控制變量的變化，平衡超曲面逐漸發生扭曲并產生折疊。最終，在超曲面上形成了3個可能的平衡位置，上下兩部分是穩定的，中間部分產生突跳，是不穩定的。跨越中間的折疊線，系統狀態就會發生突變，據此便可判斷突變是否發生，即突變判別式Δ=8u3+27v2<0時，系統發生突變。因此，水資源安全尖點突變模型的目標就是找出這個突變的區間Δ<0,從而進行系統管控，防止突變的發生。

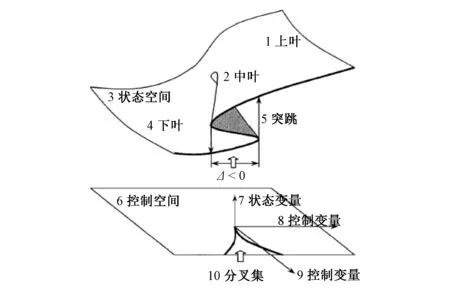
圖1 尖點突變平衡超曲面 Fig.1 Cusp catastrophe hypersurface

1.3 水資源安全突變模型變量分析

建立水資源安全分析的突變模型，首先要確定模型的狀態變量和控制變量。

突變模型的狀態變量應反映水資源與經濟發展指標的匹配程度及其對進一步發展的支撐能力。在區域水資源發展特性分析的基礎上,可在水資源及其利用、區域發展和生態環境狀況三個方面選取指標，分析區域發展的水資源支撐能力，即“水資源與社會經濟發展協調度”指標。本文選取的三方面的指標包括：綜合反映區域發展水資源條件的人均水資源量、反映水資源開發利用程度對區域社會經濟發展支撐能力的人均供水量、反映區域經濟發展富裕程度的人均GDP和反映水資源對農業發展和糧食生產保障能力的人均耕地面積，以及反映水資源對生態環境良性發展保障能力的單位面積產水量。水資源與社會經濟發展協調度層次模型如圖2。

圖2 水資源與社會經濟發展協調度層次模型Fig.2 Hierarchical model of the coordination between water resources and soci-economic development

突變模型的控制變量主要表征水資源系統的變化，而水資源系統是以水量和水質為基礎的，因此，主、次控制變量可分別選為水量指標集合和水質指標集合。在選取具體的水量、水質指標時，應綜合考慮對經濟、社會和水生態發展產生影響的多方面因素，本文選取的指標包括：人均水資源量、降雨量和單位面積產水量；人均供水量、萬元GDP耗水量和灌溉率；再生水

利用量和環境用水量；污水處理率和化學需氧量排放量；污染河長比和城市綠化覆蓋率。圖3給出了水資源安全突變分析控制變量的層次模型。水量指標方面，自然條件指標是區域水資源先天條件的直接體現，最能反映區域水資源的豐枯狀況；社會經濟指標反映了區域經濟發展狀況和水資源開發利用狀況，直接關系到城市生產和生活用水安全；生態安全是水資源安全的重要方面，但對水資源系統整體安全的作用受自然條件和社會經濟條件的影響，因此將自然條件指標和社會經濟指標置于水量指標集合中的優先位置。水質指標方面，廢、污水處理是保障區域水體不受污染最為重要的途徑，對防止區域水質惡化起著關鍵性作用，因此將污水處理指標置于水質指標集合中的優先位置。

在突變模型狀態變量和控制變量層次模型的基礎上，采用突變評價法對各層指標進行量化遞歸運算，最終得到最上層指標的值。進行歸一運算時，由于各指標的量綱不同，需要對實際指標值進行規范化處理，得到各指標的突變隸屬函數值。規范化公式如下：

圖3 水資源安全分析控制變量層次模型 Fig.3 Hierarchical model of the control variables in water security analysis

對正向型指標：X′i=(Xi-Xmin)/(Xmax-Xmin)

(5)

對負向型指標：X′i=(Xmax-Xi)/(Xmax-Xmin)

(6)

式中：X′i為各指標規范化后的值；Xi為各指標實際值；Xmax和Xmin分別為各指標逐年的最大值和最小值。

突變理論的特點是根據系統的勢函數將系統的臨界點分類，研究分類臨界點附近非連續變化狀態的特征，從而歸納出若干個初等突變模型[11]。進行綜合評價時，根據評價指標的個數，常用的突變模型有以下3種：單個評價指標(a)的折迭突變；2個評價指標(a,b)的尖點突變；3個評價指標(a,b,c)的燕尾突變。通過前述分歧方程的分解形式可導出突變理論的歸一公式，歸一公式將系統內部各評價指標的不同質態歸化為可比較的同一種質態，運用歸一公式，可求出表征系統總體特征的總突變隸屬函數值，即最上層指標值。以上三種突變模型的歸一公式如下[12]：

Xa=a1/2

(7)

Xa=a1/2,Xb=b1/3

(8)

Xa=a1/2,Xb=b1/3,Xc=c1/4

(9)

計算出X值后，根據同一子系統中各指標是否互補，即各指標的作用是否相互關聯，分別采用“大中取小”或“取平均值”原則得到上層指標的值。

2 實例研究

北京市人均水資源量不足200 m3，遠低于世界公認的人均水資源量1 000 m3的缺水警戒線，不足全國平均水平的1/10。為滿足城市供水需求，北京市常年超量開采難以補充恢復的深層地下水，造成了一系列生態環境問題，與此同時，社會經濟不斷發展，城市生產和生活用水需求居高不下。為保障北京市經濟社會的正常運行，尋求水資源安全閾值可為水資源管理提供依據。

2.1 突變模型狀態變量和控制變量計算

計算北京市水資源與社會經濟發展協調度時，各指標的協調度是相對于全國平均水平設定的，計算公式如下[13]：

Wj=Wpj/Wp,Oj=Ocj/Oc,Cj=Wj/Oj

(10)

式中：Wj為北京市人均水資源相對指數；Wpj為北京市人均水資源量；Wp為全國人均水資源量；Oj為北京市其他指標(人均GDP，人均耕地面積，人均供水量和單位面積產水)相對指數；Ocj為北京市(人均GDP，人均耕地面積，人均供水量和單位面積產水)指標；Oc為全國(人均GDP，人均耕地面積，人均供水量和單位面積產水)指標；Cj為協調度指標。

由中國統計年鑒和北京市統計年鑒查得全國和北京市2001-2014年各指標值，根據公式(10)計算得各指標協調度，規范化后根據突變評價歸一公式進行逐層量化遞推運算。北京市2001-2014年各指標協調度和水資源與經濟社會發展協調度計算結果如表1。以2001年為例，最下層各指標規范化值分別為：0.08，0.23，0.10，1.00，則中層3類指標值分別為：0.081/2=0.28，min(0.231/2,0.11/3)=0.46，1.001/2=1.00。區域發展指標、水資源利用狀況指標和生態環境狀況指標構成燕尾突變，由于任一方面的缺陷都會導致區域總體水資源支撐能力的破壞，因此應采用“大中取小”原則，則2001年北京市水資源與社會經濟發展協調度為：min(0.281/2,0.461/3,1.001/4)=0.53。

由北京市水資源公報和北京市統計年鑒查得北京市2001-2014年水量、水質指標值分別如表2、表3。

以2001年水量指標為例，最下層各指標分別構成燕尾突變、燕尾突變和尖點突變，中層自然條件指標、社會經濟指標和生態安全指標相互影響，構成燕尾突變。最下層各指標規范化后的值分別為：0.43，0.05，0.13，1.00，0，0.67，0，0，則中層3類指標值分別為：(0.431/2+0.051/3+0.131/4)=0.54，min(1.001/2,01/3,0.671/4)=0，(01/2+01/2/2)=0，2001年水量指標歸一化值為：

表1 北京市2001-2014年水資源與社會經濟發展協調度Tab.1 Values of coordination between water resources andsoci-economic development of Beijing from 2001 to 2014

表2 北京市2001-2014年水量指標值Tab.2 Water quantity index set of Beijing from 2001 to 2014

(0.541/2+01/3+01/4)/3=0.25，以此類推，可得2001-2014年北京市水量、水質指標歸一化值如圖4。

2.2 水資源安全突變分析

水資源安全突變分析的目的是通過建立表征水資源安全狀態的變量(狀態變量)與其影響因子(控制變量)之間的關系，探尋水資源狀況對社會經濟發展的影響規律，判斷水資源安全系統是否存在突變的威脅。

由尖點突變的平衡曲面4x3+2ux+v=0變換可得：

4x3=-2ux-v

(11)

式中：x為水資源系統安全尖點突變模型狀態變量即水資源與社會經濟發展協調度；u為尖點突變模型主控制變量即水量指標；v為次控制變量即水質指標。

令y=4x3,u=k1u′,v=k2v′-k3，則平衡曲面擬合式為：

y=k1(-2u′x)+k2(-v′)+k3

(12)

式中：u′為水量指標歸一化值；v′為水質指標歸一化值。

上式用矩陣表示即：

Y=XB

(13)

表3 北京市2001-2014年水質指標值Tab.3 Water quality index set of Beijing from 2001 to 2014

圖4 北京市2001-2014年水量、水質指標歸一化值Fig.4 Normalized Values of water quantity index and water quality index of Beijing between 2001 to 2014

將2001-2014年北京市水資源系統安全尖點突變模型的狀態變量值和水量、水質指標歸一化值代入式(13)，并利用Matlab中的regress函數求解得到系數矩陣B，得到擬合系數結果為k1=-1.64，k2=0.38，k3=0.16，R2為0.95，擬合效果良好，表明可以用此系數矩陣來表征狀態變量與控制變量之間的關系。由u=k1u′，v=k2v′-k3, 可得北京市水資源安全尖點突變模型主次控制變量和突變判別式Δ的計算結果，同時與各年份的供需水量差值(需水量滿足各部門用水需求)進行比較，結果見表4。

表4 北京市2001-2014年突變判別式值與水量供需差值對比Tab.4 Catastrophe indicator Δ and differences between watersupply and demand of Beijing from 2001 to 2014

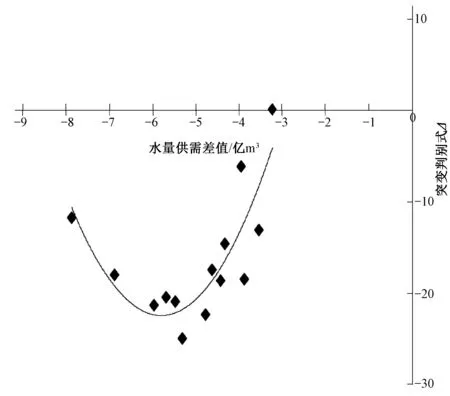
圖5 突變判別式Δ與水量供需差值關系擬合圖Fig.5 Fitting graph of Catastrophe indicator Δ and difference between water supply and demand

根據表4繪制突變判別式Δ與水量供需差值的趨勢線，采用多項式擬合，如圖5。由圖5得Δ與水量供需差值的擬合公式為Δ=2.779 4x2+32.263x+71.174，R2為0.86。由擬合公式可得當Δ=0時，水量供需差值為-2.96 億m3，此時水資源系統安全狀態處于臨界點。

2.3 遠景年份水資源安全情勢評估

建立水資源安全突變模型的目的是尋求水資源安全狀態變化的規律，防止水資源安全形勢的破壞，保障區域社會經濟發展，同時也能為遠景年份的資源規劃和管理提供依據。根據突變模型求得的水資源安全狀態處于臨界位置(Δ=0)時的水量供需差值，在對遠景年份需水量合理預測的基礎上，計算該年份安全供水的下限值，對該年的水資源安全情勢進行評估，對區域水資源規劃和可持續利用具有重要意義。

本文根據北京市2001-2014年需水量數據，采用灰色系統模型[14]，得出需水量預測模型為：Y(t)=84.739.69 e0.000 48(t-1)-84 697.55，由此預測2020年(t=20)和2030年(t=30)的需水量分別為：Y(20)-Y(19)=40.77 億m3，Y(30)-Y(29)=40.96 億m3。因此2020年、2030年北京市的安全供水下限值分別為：40.77-2.96=37.81 億m3和40.96-2.96=38.00 億m3。

查閱1988年至2014年北京市水資源公報得逐年供水量，通過頻率計算，可得北京市供水保證率與供水量對應關系如圖6，在50%、75%和90%的供水保證率下供水量分別為38.52、35.99和34.14 億m3。在50%的供水保證率對應的供水量條件下，北京市2020年和2030年的安全供水需求均能得到滿足，而在75%和90%的供水保證率對應的供水量下則會發生水資源安全破壞，75%的供水保證率下北京市2020年和2030年分別存在1.82和2.01 億m3的供水缺口，90%的供水保證率下則分別存在3.67和3.86 億m3的缺口，與《北京市“十二五”時期水資源保護及利用規劃》[15]中的預測結果相近，表明本文建立的尖點突變模型和安全評價模型合理，計算結果可為北京市水資源可持續利用規劃提供數據支撐。

圖6 北京市供水保證率曲線Fig.6 Water supply assurance rate curve of Beijing

3 結 語

(1)水資源安全研究聚焦水資源系統安全狀況對區域社會經濟發展的影響，通過探求水資源安全閾值，為區域水資源管理和規劃提供重要依據，有助于促進水資源系統和社會經濟的可持續發展，具有重要的理論和實踐意義。

(2)水資源安全突變模型通過應用突變理論中的勢函數，可建立表征水資源安全的狀態變量與其影響因子即控制變量之間的關系。狀態變量和控制變量的選取應綜合考慮與水相關的自然環境、社會經濟和生態安全等因素，從而在進行變量歸一評價時根據指標的層次結構應用突變評價的方法。

(3)依據北京市水資源開發利用的現狀，建立北京市水資源安全尖點突變模型，得出北京市水資源安全處于臨界狀態下的水量供需缺口為2.96 億m3,并對遠景年份2020和2030年的供水情勢進行了評估，得出其安全供水下限分別為37.81和38.00 億m3。

□

[1] 張玉山, 李繼清, 梅艷艷,等. 基于突變理論的天津市水資源安全閾值分析模型[J]. 遼寧工程技術大學學報(自然科學版), 2013,(4):562-567.

[2] 酈建強, 王建生, 顏 勇. 我國水資源安全現狀與主要存在問題分析[J]. 中國水利, 2011(23):42-51.

[3] Leeuwen C J V, Frijns J, Wezel A V, et al. City Blueprints: 24 Indicators to Assess the Sustainability of the Urban Water Cycle[J]. Water Resources Management, 2012,26(8):2 177-2 197.

[4] 賈紹鳳, 張士鋒. 海河流域水資源安全評價[J]. 地理科學進展, 2003,22(4):379-387.

[5] Schneider K, Turner J L, Jaffe A, et al. Choke point china: confronting water scarcity and energy demand in the world's largest country. [J]. Vermont Journal of Environmental Law, 2011.

[6] 高媛媛, 王紅瑞, 許新宜,等. 水資源安全評價模型構建與應用----以福建省泉州市為例[J]. 自然資源學報, 2012,27(2):204-214.

[7] Lu S, Bao H, Pan H. Urban water security evaluation based on similarity measure model of Vague sets[J]. International Journal of Hydrogen Energy, 2016.

[8] 孫雪峰, 于 蓮. 水生態系統的突變模型[J]. 水科學與工程技術, 2007,(1):39-41.

[9] 李繼清, 張玉山, 紀昌明,等. 突變理論在長江流域洪災綜合風險社會評價中的應用[J]. 武漢大學學報(工學版), 2007,40(4):26-30.

[10] Chen Y, Zhang S, Zhang Y, et al. Comprehensive assessment and hierarchical management of the sustainable utilization of urban water resources based on catastrophe theory[J]. Journal of the Taiwan Institute of Chemical Engineers, 2016,60:430-437.

[11] Catastrophe Theory[M]. Springer Berlin Heidelberg, 1992,196.

[12] 王文俊, 張樹深, 劉素玲,等. 基于突變理論的營口近岸海域環境災害性風險分析[J]. 農業環境科學學報, 2010,29(s1):184-190.

[13] 汪黨獻, 王 浩, 馬 靜. 中國區域發展的水資源支撐能力[J]. 水利學報, 2000,(11):21-26.

[14] 程 輝, 尚琳琳, 牛彥濤,等. 基于灰色系統模型的北京市需水量預測分析[J]. 廣東水利水電, 2013,(7):55-58.

[15] 北京市“十二五”時期水資源保護及利用規劃[J]. 北京水務, 2012,(2):13-18,23.