四湖流域旱澇交替事件特征分析

熊 威，胡鐵松，張兵堂，程曉峰

(武漢大學水資源與水電工程科學國家重點實驗室，武漢 430072)

0 引 言

受全球氣候變化和劇烈人類活動影響，我國旱澇交替事件呈現廣發、頻發的態勢，特別是近年來頻發的旱澇急轉事件，據不完全統計，近百年來長江流域旱澇急轉發生頻率達到3～4年一遇，淮河流域達到4年一遇[1,2]。因此辨識旱澇交替事件基本特征，改變傳統基于單一干旱或者洪澇災害治理理論體系與思路，對水旱災害治理具有重要價值，是我國災害治理關注的熱點與難點問題。

旱澇交替事件是一類多變量隨機事件，旱澇交替過程的持續時間、發生強度以及旱澇交替程度三者之間存在一定的相關關系，需要多特征量才能完整描述旱澇交替過程。但是目前旱澇交替事件主要是側重于旱澇交替過程單一特征的描述，如發生強度，而沒有從一個完整過程的多屬性特征角度進行完整描述。如吳志偉[3,4]提出了長、短周期旱澇急轉指數重要描述了水旱交替事件強度隨時間演變特征；王勝等[5]研究了淮河流域水旱交替事件強度空間分布特征。

Copula函數理論是描述這種相關性的一種有效方法，并得到了廣泛的應用[6-8]。本文以四湖流域為例，采用游程理論從降雨距平指標中分離出旱澇交替事件的3個特征變量，進而應用Frank Copula函數構建兩變量聯合概率分布以及三變量聯合分布，并計算相應的重現期，以期得到四湖流域水旱交替事件的持續時間、發生強度以及旱澇交替程度三者之間的相關關系，為應對地區旱澇交替災害防治工作提供一定的依據。

1 方 法

1.1 旱澇交替事件以及特征變量

旱澇交替事件作為一種隨機事件，為了全面描述其本質屬性，故定義了3個特征變量：持續時間(歷時)、發生強度以及旱澇交替程度，如圖1所示。旱澇交替歷時D為一次旱澇交替事件的總歷時，即L1、L2、L3三者之和；旱澇交替程度S為歷時D內降水距平指數(以下簡稱Pa)絕對值之和，即S1和S2之和，表示一次旱澇交替事件產生的影響；峰值I為歷時D內Pa的

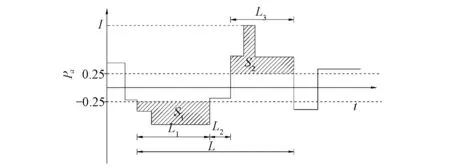
圖1 旱澇交替特征變量定義圖Fig.1 Definition of drought and flood alternating variables

最大絕對值，反映了一次旱澇交替事件中某一天所產生的最大影響。

確定了特征變量以后，下一步是選取適合的分布函數進行擬合。本文選取對數正態分布、Gamma分布和廣義Pareto分布來分別擬合旱澇交替歷時D、程度S和峰值I[9-11]，這3種分布函數計算公式分別如下：

(2)

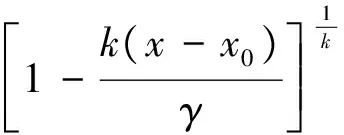
(3)

式中：μ為對數正態分布的方差；σ為標準差；α為Gamma分布的位置參數；β為尺度參數；k為廣義Pareto分布函數的形狀參數；γ為尺度參數；x0為閾值。

1.2 Copula函數理論

Copula函數式定義域為[0,1]的多維聯合分布，它可以將多個隨機變量的邊際分布連接起來構造聯合分布。其中，Archimedean Copula函數結構簡單，計算簡便，實際應用中較多。不同的Copula函數有不同的適用范圍，本文選擇Frank Copula來構造聯合分布。二維Frank Copula函數的表達式為：

(4)

相應的三維Frank Copula函數的表達式為：

(5)

其中，θ為Copula函數的參數，對于二維Copula函數的參數估計，本文采用普遍適用且相對簡便的非參數法[12]，即利用τ與θ的關系式計算θ。

對于三維Copula函數，非參數法不再適用，本文采用參數法中的IFM(Inference of Functions for Margins)方法確定三維Copula函數的參數[13]。

選定的 Copula 函數能否描述變量之間的相關性結構，需要對 Copula 函數進行擬合優度檢驗，本文采用Kolomogorov-Smirnov(K-S)檢驗方法[14]。

1.3 重現期

工程中常用重現期來描述水文事件的嚴重性。假定X1、X2和X3分別表示旱澇交替事件中具有相依關系的特征變量，u1、u2和u3分別表示旱澇交替歷時、程度和峰值的邊緣分布， 則單變量重現期計算公式[15]如下：

(6)

式中：TXi為單變量重現期；N為系列長度，a；n為發生旱澇交替事件的次數，i=1,2,3。

對于二維聯合分布的重現期，以X1和X2的組合重現期為例，有“X1>x1或X2>x2”和“X1>x1且X2>x2”兩種情況，對應的二維變量聯合重現期和同現重現期計算公式[16]分別為：

(8)

三維變量聯合重現期和同現重現期的計算公式[17]分別為：

(9)

(10)

2 特征變量聯合分布模型

本文以四湖流域監利站為例，以降水距平指數[18]作為診斷量，從該站1957-2013年的逐日降雨資料中挑選出52次旱澇交替事件。借助于游程理論[19]從Pa序列中分離出旱澇事件，挑選標準如下：若前期干旱歷時L1(洪澇歷時L3)在10 d以上，并在10 d內經過天數L2由旱轉為澇(澇轉為旱)，且洪澇歷時L3(干旱歷時L1)在10 d以上，則選為一次旱澇交替事件。

2.1 單變量邊緣分布

分別用對數正態分布來擬合旱澇交替歷時D，Gamma分布來擬合旱澇交替程度S，廣義極值分布來擬合旱澇交替程度I。對數正態分布采用極大似然法估計參數，其余均采用矩法估計參數。參數以及擬合結果見表1，結果表明，3種分布均通過了α=0.05顯著性檢驗(n=52，Dmax<0.196)，即對旱澇交替歷時、程度以及峰值的擬合效果良好。

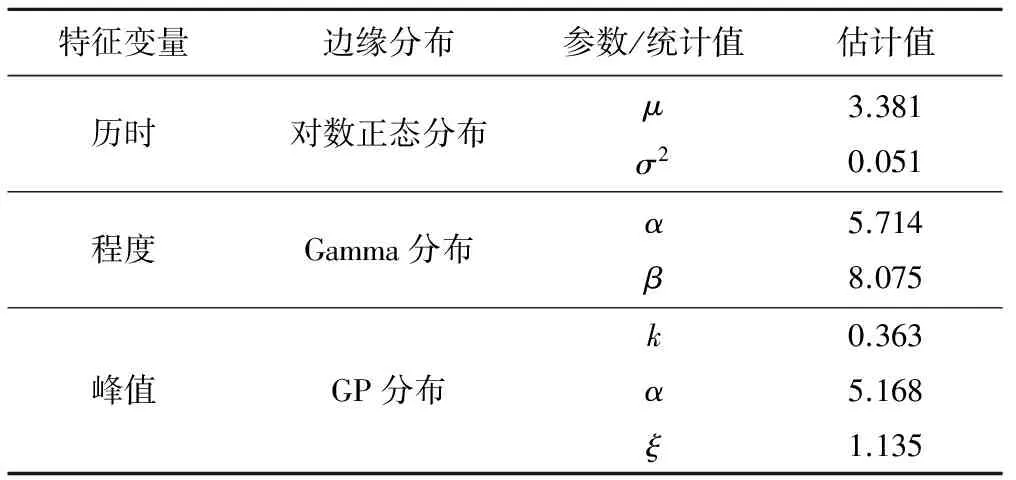
表1 邊緣分布函數參數值Tab.1 Estimated parameters for marginal distribution function

2.2 Copula聯合分布函數及擬合檢驗

2.2.1 二維模型

二維Frank Copula函數采用非參數法進行參數估計，參數計算結果和擬合效果見表2。結果表明，3種擬合情況下的Frank Copula函數均通過α=0.05顯著性檢驗(n=52，Dmax<0.196)，即擬合效果良好。

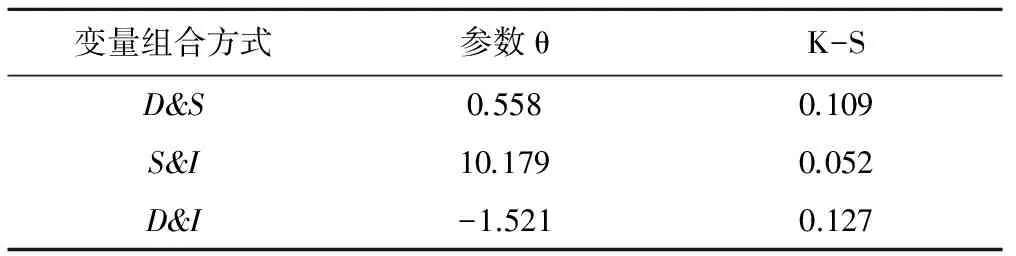
表2 二維Frank Copula函數參數和K-S檢驗結果Tab.2 Parameters of two-dimension Frank Copulafunction and the K-S fitting results

2.2.2 三維模型

根據IFM方法計算得到三維Frank Copula 函數的參數θ值為3.072，并采用K-S檢驗進行擬合檢驗，其檢驗值為0.113，表明三維Frank Copula函數達到了α=0.05顯著性水平(n=52，Dmax<0.196)，即擬合效果良好。

3 旱澇交替特征值的頻率分析

3.1 旱澇交替事件概況

監利站從1957年到2013年共發生52次旱澇交替事件，約1.1 a一遇，平均歷時為33.85 d，平均程度為49.31，平均峰值為5.18。其中，旱轉澇事件占絕大多數，占總數的62%，其余為澇轉旱事件。

從年內分布來看，如表3所示，旱澇交替事件主要集中在夏季，占總事件數的46%，冬季發生的次數最少；夏季旱澇交度替事件平均歷時為30.13 d，平均程度為58.21，平均峰值為7.01，平均程度和平均峰值均大于其他季節。從年間分布來看，如圖2所示，旱澇交替事件2000年以前年代見發生次數大致相同，2000以后有增加趨勢；20世紀80年代以前旱澇交替事件分布較為均勻，80年代以后分布較為集中；旱澇交替歷時和程度在2000年以后變化越來越劇烈。

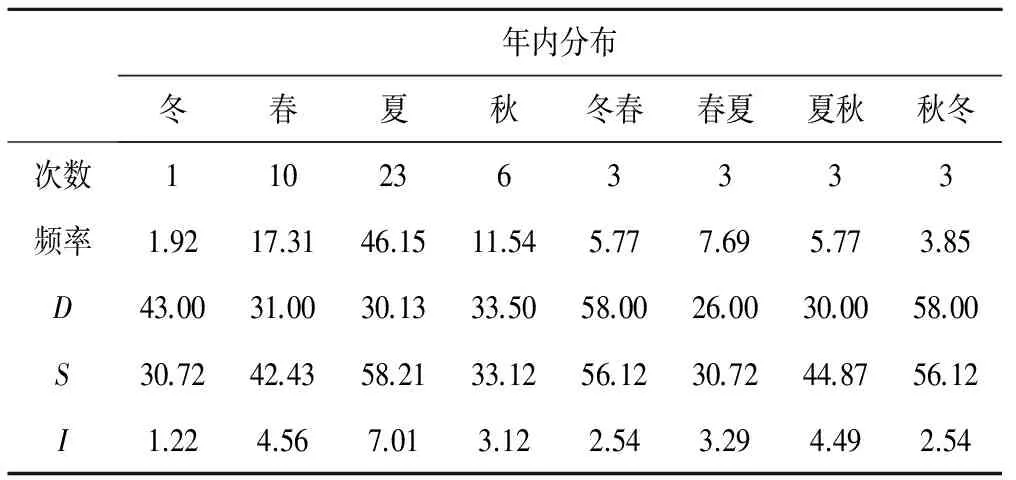
表3 旱澇交替事件年內分布情況Tab.3 The probability of drought and flood alternating events

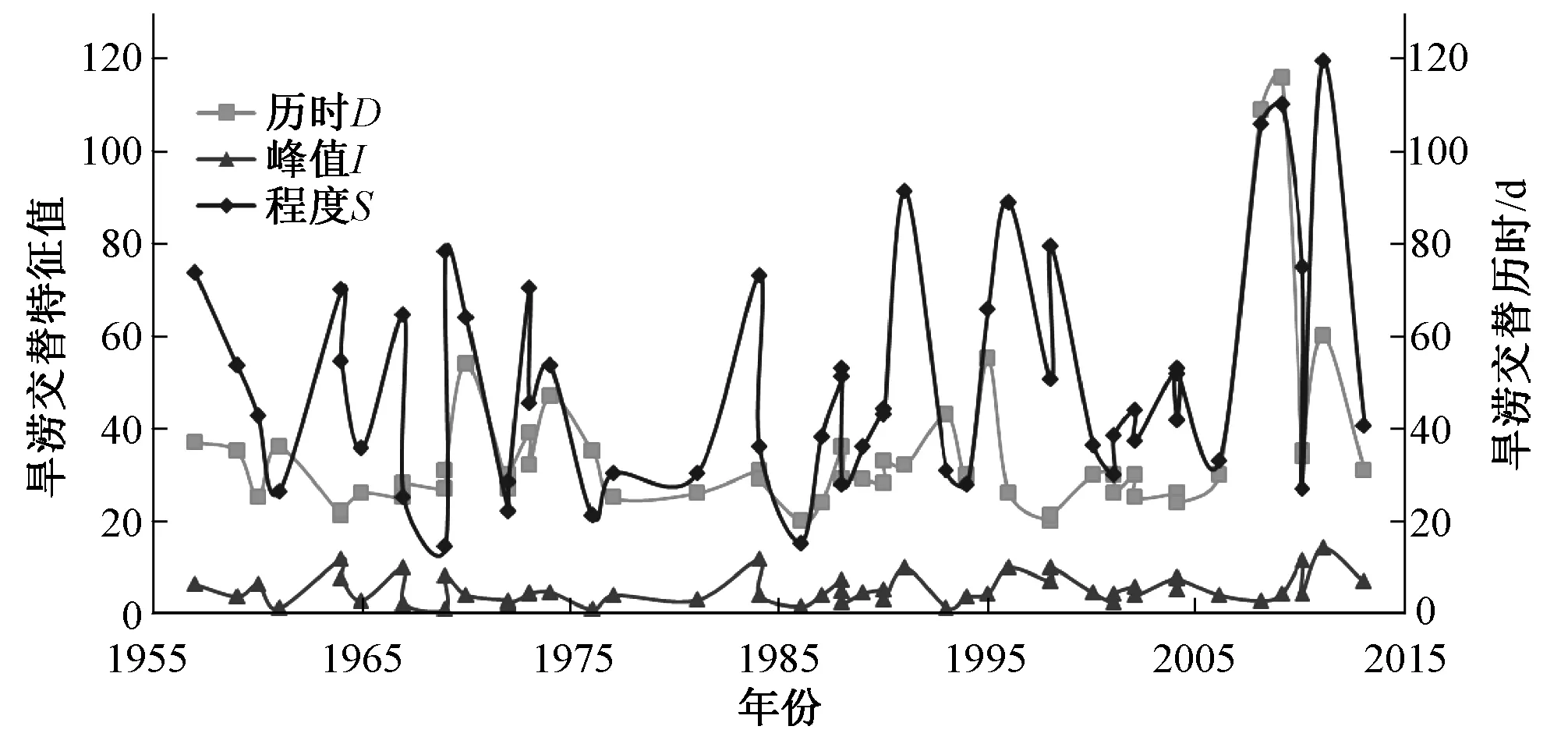
圖2 旱澇交替特征值變化趨勢Fig.2 The tendency of drought and flood alternating variables

3.2 二維變量聯合概率分布

根據式(1)計算得到二維聯合分布函數，分別將旱澇交替D-S、D-I、S-I的聯合不超越概率以及聯合超越概率繪于圖3～圖5中，從二維平面投影圖上可以查出三個特征變量兩兩組合的聯合不超越概率和聯合超越概率。由圖3可知，常見的旱澇交替事件歷時小于33 d，程度小于56，此類事件占所有事件的50%左右；而歷時小于39 d，程度小于74的旱澇交替事件約占所有事件的80%；歷時60 d以上，程度大于91的旱澇交替事件極少發生。

由圖4可知，常見的旱澇交替事件程度小于50，峰值小于5，此類事件占所有事件的50%左右；而程度小于72，峰值小于9的旱澇交替事件約占所有事件的80%；程度大于92，峰值大于12的旱澇交替事件極少發生。

由圖5可知，常見的旱澇交替事件歷時小于32 d，峰值小于7，此類事件占所有事件的50%左右；而歷時小于39 d，峰值小于10的旱澇交替事件約占所有事件的80%；歷時60 d以上，程度大于91的旱澇交替事件極少發生。

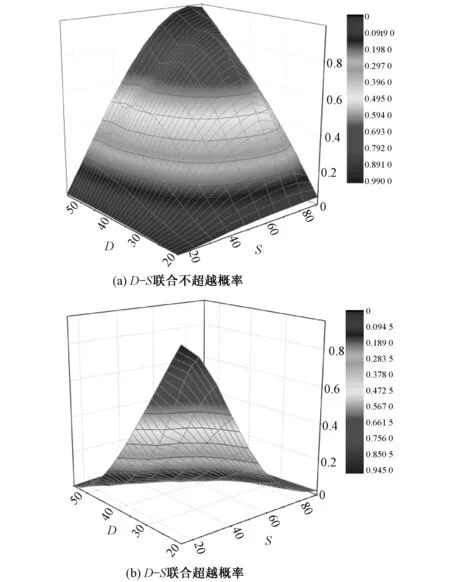
圖3 D-S聯合分布概率三維圖Fig.3 The joint probability of D-S

圖4 S-I聯合分布概率三維圖Fig.4 The joint probability of S-I

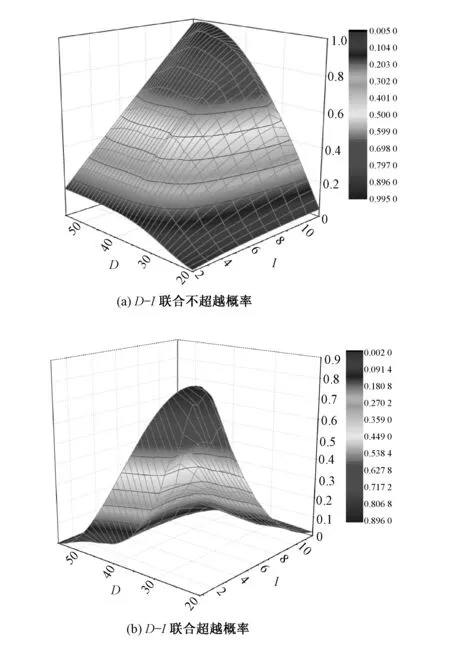
圖5 D-I聯合分布概率三維圖Fig.5 The joint probability of D-I

3.3 組合重現期

在相同單變量重現期下，兩個和三個特征變量同時發生的組合重現期的計算結果見表4。可以看出，單變量重現期介于兩種多維變量的重現期之間，故可根據組合重現期來估計單變量重現期的范圍。綜合對比4種組合重現期，隨著單變量重現期的增加，D-I的組合重現期增幅最大，其次是D-S，S-I的增幅最小，說明S與I同時發生的風險最高，與前面的分析一致；D-I的組合重現期范圍最大，例如單變量重現期為20 a時，同現重現期達到了500 a以上，這與D與I呈負相關有關。由3.1可知，考慮比較容易發生的特征變量即單變量發生頻率達到80%時，旱澇交替事件的D小于33.57 d，S小于61.13，I小于7.44，對應的組合重現期見表6，可以看到，監利站大部分旱澇交替事件的聯合重現期介于2～5 a之間，同現重現期介于48～100 a之間。

3.4 典型年頻率分析

三個特征變量值越大，產生的影響越大，故將特征變量較大的10次旱澇交替事件列在表7中，可以看出，2011年的3個特征變量值均排在前列，旱澇交替產生的影響嚴重，這與實際相符：2011年春末至夏初，長江中下游地區發生一次旱澇急轉現象，給人民生命、財產帶來了重大損失[20]。故以2011年為旱澇交替典型年，其特征變量為典型特征變量，分別記為D0、S0和I0。對典型年進行頻率分析，結果見表8。可以看出，若發生比2011年特征變量值更大的旱澇交替事件，D-S同時超過事件的發生概率與I-S同時超過事件的發生概率接近，分別為0.31%和0.35%，D-I同時超過事件的發生概率三者中最小，這間接反映了三變量之間的相關性：相關性越強，二維聯合分布概率越大。三變量值同時超過事件的發生概率很小，接近于0。

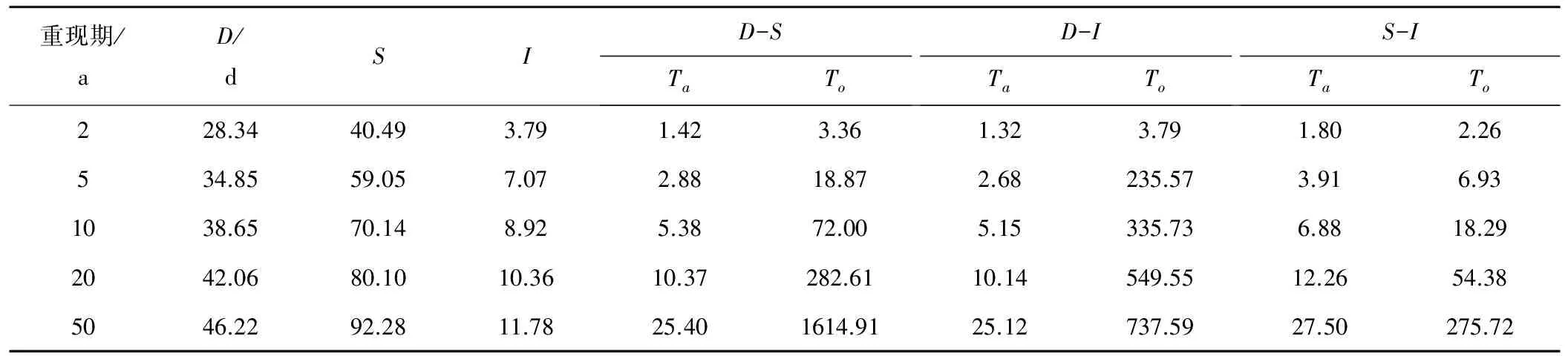
表4 單變量重現期以及相應二維變量的組合重現期Tab.4 Calculated results of the return periods of two-dimension joint distribution

注：Ta為聯合重現期，To為同現重現期。

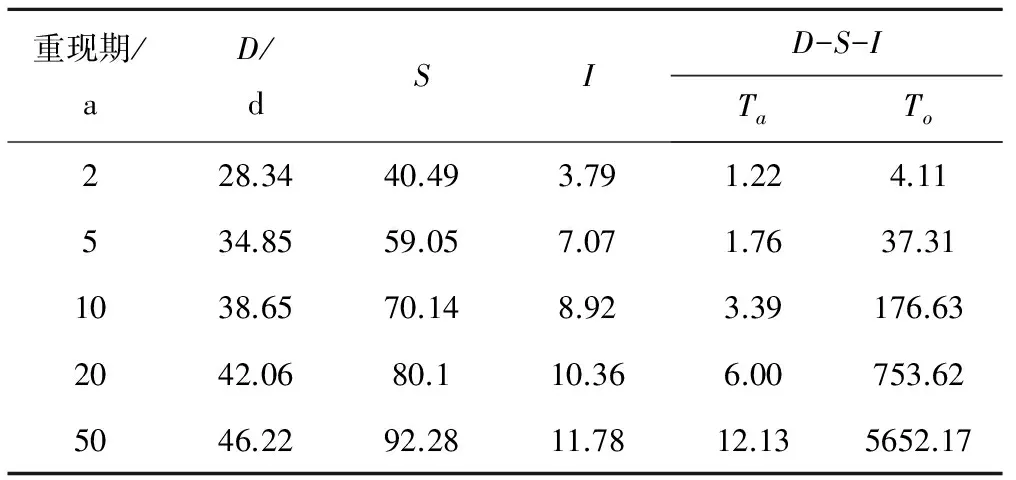
表5 單變量重現期以及相應三維變量的組合重現期Tab.5 Calculated results of the return periods ofthree-dimension joint distribution

表6 給定特征變量的多維變量組合重現期Tab.6 The return periods of multi-dimension jointdistribution with given variables

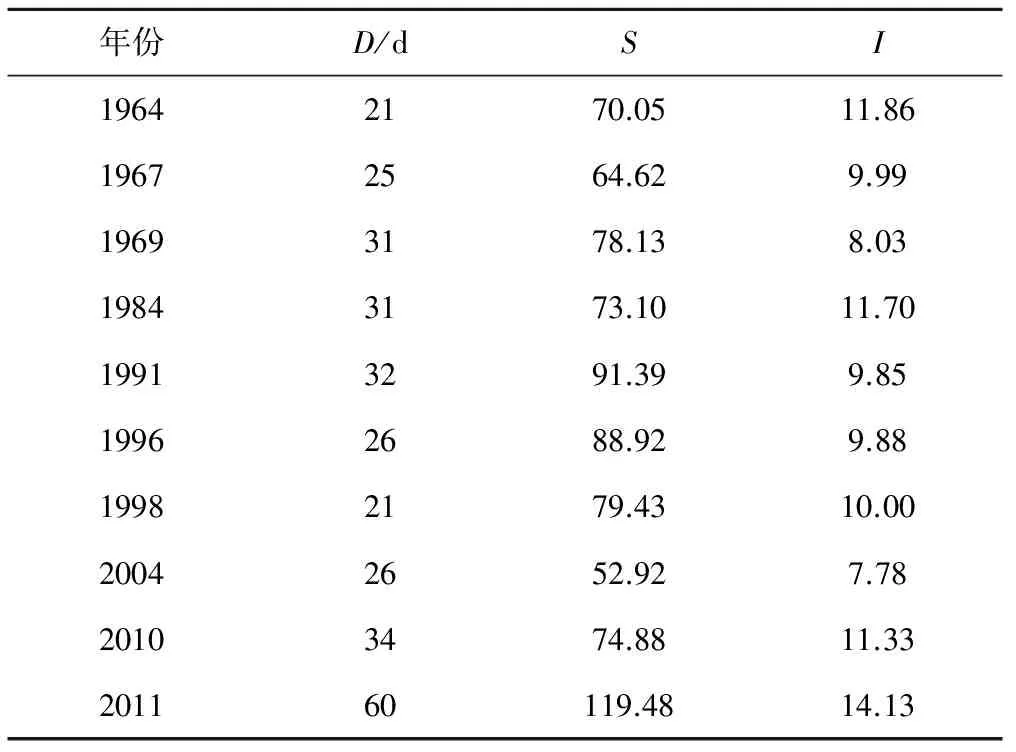
表7 監利站旱澇交替事件的特征變量Tab.7 Variables of drought and flood alternatingevents at Jianli Meteorological stations

表8 典型年旱澇交替事件頻率Tab.8 Probability of the typical drought and flood alternating event

注：D0、S0和I0為2011年時時澇交替事件的特征變量；D0=60，S0=119.48，I0=14.13。

4 結 語

本文基于游程理論從監利站1957-2007年的降雨距平序列中挑選出了旱澇交替事件，定義了旱澇交替特征變量，并應用二維以及三維Frank Copula函數構建了旱澇交替特征變量的聯合分布模型，基于該聯合分布模型，分析了旱澇交替事件的頻率，結果表明：

(1)監利站共發生52次旱澇交替事件，約1.1 a一遇，平均歷時為33.85 d，平均程度為49.31，平均峰值為5.18。旱轉澇事件占絕大多數，從年內分布上看，主要集中在夏季，冬季發生的次數最少；從年間分布上看，旱澇交替事件呈現出歷時變長，程度變大，分布越來越密集的態勢。

(2)旱澇交替事件作為隨機水文事件，其特征變量間具有相依關系，用Frank Copula函數構造的兩變量聯合分布以及三變量聯合分布擬合精度是滿意的。通過聯合分布計算得到監利站旱澇交替事件多為歷時小于39 d、程度小于74，或者程度小于72、峰值小于9，或者歷時小于39 d、程度小于74的旱澇交替事件，這3種情況均占所有事件的80%左右。

(3)單變量重現期介于兩種多維變量的重現期之間，可根據組合重現期來估計單變量重現期的范圍；監利站大部分旱澇交替事件的聯合重現期介于2～5 a之間，同現重現期介于48～100 a之間。

(4)2011發生的年旱澇交替事件歷時達到60 d、程度達到119.48、峰值達到14.13，歷史上極為罕見，若發生比其特征變量值更大的旱澇交替事件，D-S同時超過事件的發生概率為0.31%，I-S同時超過事件的發生概率為0.35%，D-I同時超過事件的發生概率為0.20%，三變量值同時超過事件的發生概率接近于0。

需要指出的是，本文僅從氣象干旱出發，沒有考慮農業、水文以及社會等方面的綜合影響，今后應進一步深入研究。

□

[1] 程 智, 徐 敏, 羅連升,等. 淮河流域旱澇急轉氣候特征研究[J]. 水文, 2012,32(1):73-79.

[2] 曾凡榮. 湖北水利志[M]. 中國水利水電出版社, 2000.

[3] 吳志偉, 李建平, 何金海,等. 大尺度大氣環流異常與長江中下游夏季長周期旱澇急轉[J]. 科學通報, 2006,51(14):1 717-1 724.

[4] 吳志偉. 長江中下游夏季風降水“旱澇并存、旱澇急轉”現象的研究[D]. 南京：南京信息工程大學, 2006.

[5] 王 勝, 田 紅, 徐 敏,等. 1961-2008年淮河流域主汛期極端降水事件分析[J]. 氣象科技, 2012,40(1):87-91.

[6] 閆寶偉, 郭生練, 肖 義,等. 基于兩變量聯合分布的干旱特征分析[J]. 干旱區研究, 2007,24(4):537-542.

[7] 張 翔, 冉啟香, 夏 軍,等. 基于Copula函數的水量水質聯合分布函數[J]. 水利學報, 2011,42(4):483-489.

[8] 王 珍, 李久生, 栗巖峰. 基于三維Copula函數的滴灌硝態氮淋失風險評估方法[J]. 農業工程學報, 2013,29(19):79-87.

[9] Mayer P, Mayer H. Radar target detection-handbook of theory and practise[M].New York:Academic Press,1973:1-108.

[10] Emir Z, Atila S. A method of streamflow drought analysis[J]. Water Resources Research, 2010,23(23):156-168.

[11] Mannshardt-Shamseldin E C, Smith R L, Sain S R, et al. Downscaling extremes: a comparison of extreme value distributions in point-source and gridded precipitation data[J]. Annals of Applied Statistics, 2010,4(1):484-502.

[12] Genest C, Rivest L P. Statistical inference procedures for bivariate archimedean copulas[J]. Journal of the American Statistical Association, 2012,88(423):1 034-1 043.

[13] 楊益黨, 羅羨華. Copula函數的參數估計[J]. 新疆師范大學學報:自然科學版, 2007,26(2):15-18.

[14] Singh V P, Zhang L. Bivariate flood frequency analysis using the copula method[J]. Journal of Hydrologic Engineering, 2006,11(2):150-164.

[15] Shiau J T, Shen H W. Recurrence analysis of hydrologic droughts of differing severity[J]. Journal of Water Resources Planning & Management, 2014,127(1):30-40.

[16] Shiau J T. Return period of bivariate distributed hydrological events[J]. Stochastic Environmental Research & Risk Assessment, 2003,17:42-57.

[17] 李 計, 李 毅, 賀纏生. 基于Copula函數的黑河流域干旱頻率分析[J]. 西北農林科技大學學報:自然科學版, 2013,(1):213-220.

[18] 鞠笑生, 楊賢為, 陳麗娟,等. 我國單站旱澇指標確定和區域旱澇級別劃分的研究[J]. 應用氣象學報, 1997,(1):26-33.

[19] Herbst P H, Bredenkamp D B, Barker H M G. A technique for the evaluation of drought from rainfall data[J]. Journal of Hydrology, 1966,4(66):264-272.

[20] 封國林, 楊涵洧, 張世軒,等. 2011年春末夏初長江中下游地區旱澇急轉成因初探[J]. 大氣科學, 2012,36(5):1 009-1 026.