山區河流防洪避難逃生系統研究
范 強, 田 忠,唐南波,丁 燦
(四川大學水力學與山區河流開發保護國家重點實驗室,成都 610065)
洪水災害對人類的嚴重影響由來已久,就災害發生的時空范圍、強度以及對人類生存與發展的威脅程度而言,洪水災害居各種自然災害之首。我國是一個多山地國家,山區面積占到了國土陸地總面積的2/3[1]。山區河流因其具有獨特的特點,在暴雨期匯流速度快,能在較短時間內形成大規模洪水,而且山區河流匯流過程難以監測,形成洪水后留給下游及兩岸洪泛區居民撤離轉移的時間非常短。因此,撤離工作的成功與否,關鍵在于能否制定出合理有效的撤退計劃以及在計劃實施過程中對突發事件的應對能力。
針對山區河流水頭高、落差大、破壞力強的特點,在研究防洪避難逃生系統時要充分考慮下游居民短時間內的避難效果。洪水來臨時,為高效、有序地疏散淹沒區內的災民,在綜合分析避難逃生過程中各影響因素的基礎上,對山區河流的防洪避難逃生系統進行了研究,并提出了科學規劃防洪避難安置點的選址原則與安置點內的人口優化方法。
1 防洪避難系統
本研究選用動態規劃中的最優控制方法[2],為洪水淹沒區內的居民避難設計了相對最優的避難路徑。選用的目標函數使得避難路徑最短,相對而言,實施避難時最為省時。
1.1 點線結合型防洪避難模型
點線結合型洪災分析方法是在洪水淹沒范圍模擬計算的基礎上,確定出需要轉移的居民點及避難點。由于山區鄉鎮的地勢、人口及道路情況差別往往較大,因此在設計防洪避難系統時不能單純的把各村莊、避難點看作點,而應看作具有不同容量的點;道路上分布著撤退的居民、車輛、牲畜等,也不能單純的把各條道路看作線,而應看作具有不同輸運能力的線。因此,根據淹沒區各村莊的地理位置關系,以及各村莊的道路分布情況,以靠近道路的特征點來代表該村莊,以道路網密度作為淹沒區的輸運指標。道路網密度高說明道路密集,有利于該村莊的人員及物資轉移撤離。
對于淹沒區內的居民點,其達到避難點的最優路徑屬于不固定的最優路線問題,因而選用函數空間迭代法模型[3]進行求解,原理如下:
給定點集G,其個數為N,記為G={1,2,…,N},任意2點i,j之間用弧段連接,長度記為lij,0 (1) 令: (2) 作為初始函數f1(i),1 (3) 式中:fk(i)表示由i點出發最多經過k個點的最短路徑(不一定到達N點)。 可證得式(1)、(2)、(3)確定的函數列{fk(i)}單調遞減,且收斂于f(i)。f(i)為式(1)的解,{fk(i)}不超過N-1步收斂于f(i)。 具體到淹沒區村莊居民的避難問題,將已確定的各村莊特征點及各條道路連接成網狀,各道路之間的交叉點以及各村莊均作為節點考慮,則可很直觀地將節點之間的距離視為上述各式中的lij。因此,一旦確定了各避難方案中的具體避難點后,就可按上述遞推原理一一求出各點到達避難點的最短距離。 在實際避難逃生過程中,計算從淹沒區居民點到避難點之間的最佳撤離路線,不僅要計算多點間在交通順暢的道路網中的最短距離,也要考慮災害發生后,洪水對道路通行能力的影響。如果洪水沖垮道路網中的某幾段道路,或者有些道路因洪水淹沒造成路段積水,都會使得避難人群及車輛的通行能力下降。 目前最短路徑的算法中,最經典也是運用最成熟的算法是Dijkstra提出的按路徑長度依此遞增的最短路徑法。Dijkstra算法[4]適用于所有弧的權重為非負的最短路徑算法,可以給出從某定點到途中其他所有頂點的最短路徑。Dijkstra算法的基本思想是標記源點到已知點的最短路徑,再依次尋找另一個點的最短路徑。其主要特點是以起始點為中心向外層擴展,直到擴展到終點為止,見圖1。 若已知圖1中對總長度最接近于定點s的m個頂點,以及從定點s到這些頂點中每一個頂點的最短路徑,對定點s和這m個定點標記。然后從最接近于s的m+1個頂點可求之如下:對于每一個未著色的頂點y,考慮所有已著色頂點x,將弧(x,y)接在從s到x的最短路徑后面。這樣,就構成了從s到y的最短路徑。 從s到某一個未著色的頂點使它按以上所述算出的路徑最短,則這個頂點就是最近接于s的第m+1個頂點。因為所有弧的長度都是非負值,所以從s到最接近于s的第m+1個頂點的最短路徑必然只是用所得的頂點作為其中間頂點。所以,如果最接近于s的m個頂點為已知,則第m+1個頂點可按上述方法確定。從m=0開始,將這個過程重復下去,直至求得從s到t的最短路徑為止。 路徑分析是防洪避難系統中最基本的功能,路徑最短尋優是一種靜態尋優,與實時的道路交通狀況無關,只與淹沒區道路網有關;時間最短尋優是一種動態尋優,與實時交通狀況有著密切的聯系。行程時間最短尋優是一種動態尋優,通常隨著道路網中流量的變化而變化,當道路網中某段路不能正常通行時就會動態計算出其他可行的疏散路徑,重新規劃疏散方案。 動態路徑分析模型是在路權模擬的基礎上進行的。該模型隨著模擬的時間進程,動態記錄各路段上的交通負荷。一旦交通負荷發生變化,立即調用路權模型計算新的路權,并對路段的阻力進行更新,從而達到動態分析交通狀況的效果。 車輛行駛的自由程度與相近車輛的距離有關,正常情況下,當相近的兩車距離越大,其干擾度越小,車輛行駛的自由程度就越高。基于這樣的認識,利用隨機度來表示車輛自由行駛的程度,即: (4) 式中:R為車流隨機度;n為車輛總數;f(hi)為車間影響函數[5]。 f(hi)可表示為: (5) 式中:hi是車輛間距;h0為車輛互補影響的臨界車距;hmin是車輛保持安全行駛的最小車距;當hi≥h0時,f(hi)=0;當hi 根據各時段的車距情況,可將路網預警水平劃分成4個等級,分別為:通暢、一般通暢、一般擁堵、擁堵,不同預警水平用不同的信號燈表示,各信號燈含義如下: “綠燈”:當0.8 “黃燈”:當0.5 “黃燈閃爍”:當0.2 “紅燈”:當0 以道路網數據為基礎,利用路阻函數模型計算出各時段的路權。在此基礎上,根據預警系統判斷出該道路的預警級別,當道路處于“暢通”、“一般暢通”狀態時,車流及人群撤離迅速,不需要調用路阻函數計算新的路權。當預警級別為“一般擁堵”、“擁堵”狀態時,車流及人群撤離受阻,需要調用路阻函數計算新的路權,并對道路網數據庫進行修正更新,從而得到實時的道路信息數據,從而實現對災民撤退全過程的動態跟蹤模擬。 山區避難場所的選擇應引入科學的規劃方法進行布局,使有限的安全保障資源最大限度地為災民提供避難服務。避難場所應選擇地勢較高、交通較為便利處,所屬的配套設施應盡可能齊備,包括:避難生活設施、指揮和通信設施、疏散保障設施、醫療救護設施及運輸場地設施等[6,7]。 避難場所的規劃選擇及空間配置,應充分考慮以下原則。 (1)綜合防災,統籌規劃,將避難點的選擇作為一個系統性工程,要充分考慮到避難點之間的人員、物資轉移情況。 (2)與山區平整地規劃相協調,在功能上要實現平、災結合。 (3)因地制宜,選址安全,要確保避難點不受洪水侵襲,不能讓災民多次搬遷。 (4)避難點高程選擇不能太高,其地面高程只要高于“洪水位+安全超高”即視為安全,這樣既方便建設,也方便救災物資的運輸。 (5)受災人員需合理安置,不能簡單就近安排,安置點具有一定容量,不能無限制接納災民。 (6)明確救災點及責任區區劃,以確保發生洪水時相關防災機構能及時指揮災民撤離。 (7)應急避難與長期防災相結合,明確避難場所的分類分級,根據人口分區,將避難點分為臨時聚集點、臨時避難點、永久避難點3級。 (8)避難場所可持續發展的關鍵是要與避難場所的資源承載能力相協調,要控制好安置區內的人口數量,使人口維持在資源承載力所能接受的范圍之內。 避難安置區地勢較高,有效抵御了洪水侵犯,安置區的道路便于人員、物資進出,這種現象可以用界殼理論[8]來分析。界殼理論是研究系統周界的一般性理論,它從全新的觀點來討論系統的平衡問題。界殼被定義為處在系統外圍能衛護本系統,且與環境進行交換的中介體,它是系統的周界,是系統的一部分。避難安置區系統的界殼處在安置區系統和外圍的交界處,由界壁及界門組成。安置區系統界殼的界壁主要為系統的邊緣周 界,如河岸、堤壩等;系統界殼的界門主要為堤、壩的閘門和通往外界的道路等。安置區的人口變化與移民控制是一個典型的界殼論問題,移民的交換律可以簡單地表示為: α=(Iin+Iout)/2 (6) 式中:Iin為移入率;Iout為移出率。 人口的動態變化可以用指數函數來表示,為使安置區內的人口不超過安置區的承載力,規定當人口增量超過某一值c0時停止災民進入,這樣的模型可表示為: (7) 式中:Δx/Δt為t時段內進入安置區的人數;k為該安置區的安置系數。 這里δ起到開關函數的作用,當Δx/Δt≤c0時,δ=1;當Δx/Δt>c0時,δ=0。即當δ=1時,災民可繼續進入該安置區;當δ=0時,該安置區達到該安置區安置能力的上限,災民需進入其他安置區避難。 鹽邊縣位于四川省涼山州西部,隸屬于攀枝花市,是二灘水電站庫區的主要淹沒縣。全縣面積3 344 km2,轄4個鎮,12個鄉,164個村和7個居民委員會,總人口20.19萬人;成昆鐵路橫貫境內,雅攀高速公路通過縣境。鹽邊縣地勢北高南低,由西北向東南傾斜,為我國西南部山區典型的山區城市,在洪水期極易受到山區洪水的侵襲。 二灘水電站位于雅礱江下游,壩高240 m,總庫容58 億m3。當雅礱江流域進入汛期后,若暴雨產生的大洪水迅速從上游傳至二灘庫區,且來水量超過二灘庫區的防洪庫容,為避免因超標洪水造成的潰壩淹沒攀枝花市區,必須進行緊急泄洪。 下泄洪水與雅礱江原河道上漲河水迅速向下游傳播,鹽邊縣首當其沖,二灘壩址距鹽邊縣城北32 km,經洪水演算分析:鹽邊縣城應急轉移時間為35 min;鹽邊縣城位于雅礱江左岸,最近距離500 m,此時需將縣城5.2萬人口迅速進行轉移至距雅礱江河道5 km外的避難安置點。 根據鹽邊縣城的人口分布、建筑物布局及路網狀況將縣城劃分為7個區,選取各區內靠近轉移道路的居民點作為代表點,根據各區內的道路分布情況將它們分成7個轉移點。為簡化計算,假定淹沒區域內的所有道路屬性一致。淹沒區分區、洪水淹沒情況及避難安置點的分配見圖2。 圖2 避難逃生示意圖Fig.2 Schematic diagram of evacuation escape 利用Dijkstra法計算出最短路徑和最短遷移距離,根據淹沒區路網某時刻的路阻函數,利用動態路徑分析模型,能夠計算出撤退過程中路網的路權,最后計算出最短的遷移時間,研究結果見表1。 表1 鹽邊縣城防洪避難決策方案指標Tab.1 Yanbian County flood refuge decision-making index 災民撤退與安置的第1要求是確保轉移人員的生命安全,在撤退過程中要盡量避免各轉移點同時選擇同一道路撤退而造成交通擁堵。因此,在撤退過程中要妥善安排各分區的出發順序,以避免發生擁堵,影響撤退速度。 在災民進入安置區后,要充分重視安置區的人口優化配置,在某安置區達到安置能力上限時,應及時組織災民撤往其 他備用安置區。為保證安置區的可持續發展,應充分論證安置區的生態系統能否承載相應的災民人數,以確保該安置區的永續利用。 本研究選用動態規劃中的最優控制方法,為洪水淹沒區的居民設計了相對最優的避難路徑。并以鹽邊縣城作為實例進行了防洪避難系統的研究,研究結果表明,本文所建立的模型可以有效解決淹沒區災民撤的退問題。防洪避難系統的研究和開發在我國剛剛起步,本研究所建立的模型仍處于基礎研究階段,在接下來的研究中將綜合考慮更為復雜的各項因素,使洪災避難系統更臻完善。 □ [1] Li Fawen. Study on the theory and application of flood disaster evacuation decision[D].Nanjing: College of Water Resource and Environment, Hohai University, 2005. [2] 謝林柏, 趙維一, 紀志成.基于δ算子的網絡控制系統最優控制方法[J].東南大學學報, 2006,36(增刊). [3] 何少苓, 劉樹坤,廖文根,等.防洪避難系統在東平湖滯洪區的運行[J].水利學報, 1994,(10):36-39. [4] Zhan F B. Three fastest shortest path algorithms on real road networks[J].Journal of Geographic Information and Decision Analysis, 1997,1(1):69-82. [5] 楊佩昆, 黃文忠. 城市道路車隊離散過程中的交通流模型[J].同濟大學學報, 1994,9(3):294-299. [6] Yao Qinling. Urban calamity decrease layout[J].Urban Layout, 1995,(3):39-40. [7] 蘇幼坡, 劉瑞興. 城市地震避難場的規劃原則與要點[J].災害學, 2004,19(1):87-91. [8] 曹鴻興.系統周界的一般理論——界殼論[M]. 北京:北京氣象出版社, 1993.1.2 Dijkstra算法求解最短路徑
1.3 防洪避難路阻函數計算模型
2 避難場所的選擇
3 安置區人口的優化
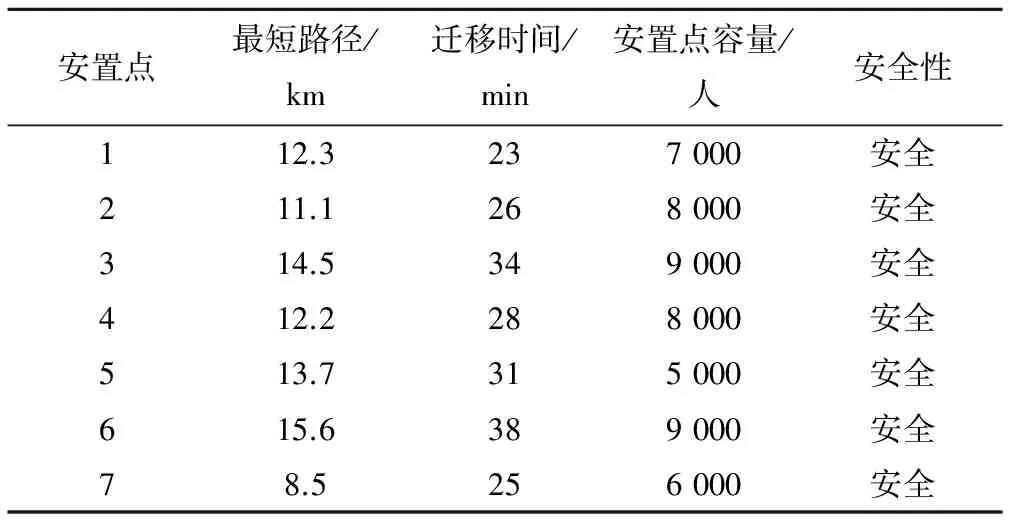
4 應用實例

5 結 語

