基于非穩定過程的巖土體非飽和參數反演分析
馬恒臻,劉明明,陳 君,王旭輝
(1. 武漢大學水資源與水電工程科學國家重點實驗室,武漢 430072;2. 武漢大學水工巖石力學教育部重點實驗室,武漢 430072)
0 引 言
非飽和滲流問題一直是水利工程、巖土工程、環境工程研究的熱點,其在壩體滲流、降雨入滲、淺層地下水污染治理等領域有著廣泛的應用[1]。過去幾十年中,大量關于非飽和滲流的研究[2-4]主要集中于各種非飽和土體,并且對于非飽和土的持水特征曲線有相對成熟的試驗測定技術[6,7]。但對于巖體,由于其結構特征、孔隙和裂隙發育程度不均一,天然性質極其復雜,導致巖體的非飽和水力特性的確定及其非飽和參數的試驗測定非常困難。因此,研究巖體非飽和水力參數的確定方法具有重要意義。孫樹林等[8]基于巖體微觀結構和毛細管理論得到了裂隙孔隙巖體持水特征曲線。王恩志等[9]對裂隙巖體非飽和滲流中應用V-G模型和B-C模型進行評價并建立了改進的本構關系。根據現階段研究成果,壓汞試驗可以確定孔隙性巖體的持水特征曲線,但試驗過程困難。另外,天然巖體中孔隙、裂隙的發育存在極大的不均勻性和復雜性,小尺度測定技術難以反映現場條件下巖體的非飽和水力特性。
另一方面,在實際工程中,以實測水位為已知信息來確定現場尺度下巖土體滲透特性的反饋分析方法已經有了廣泛應用。張乾飛等[10]基于人工神經網絡的非線性映射特性提出了大壩滲透系數的反演方法。劉杰等[11]利用水頭實測資料,運用遺傳算法反演了裂隙巖體滲透系數。上述方法多用于確定滲流場中各巖土介質的飽和滲透系數,而將實測水位信息反饋分析方法用于巖土體非飽和參數確定方面的研究報道較少。
本文在非飽和滲流的框架下,建立了正交設計、非飽和滲流正分析、BP神經網絡和遺傳算法優化相結合的反演分析方法,確定了基于V-G模型[4]的巖土體持水特征曲線參數。該方法首先以研究區域的水文地質條件為基礎,確定待求的巖土體非飽和參數及其合理的變化范圍;其次運用正交設計生成樣本組,其中每個樣本和一組參數組合相對應;然后對每個樣本采用非飽和有限元滲流分析來模擬其滲流場的變化過程,得到相應監測點處的計算結果及其變化曲線;進而將各個樣本對應的參數組合作為輸入,監測點處的水頭值作為輸出,訓練BP神經網絡;最后通過訓練得到的BP神經網絡來預測任意參數組合下的計算值,并以接近監測資料為目標,采用遺傳算法獲得最佳非飽和參數取值。本文以一次降雨過程中巖質邊坡非飽和滲流場的動態變化為例,論證了該方法的可行性和可靠性。
1 非飽和滲流理論及其反問題
1.1 飽和/非飽和滲流數學模型
根據質量守恒定律,可建立巖土體區域Ω內飽和/非飽和滲流的控制方程:
▽·v=0 (inΩ)
(1)
式中:φ=h+z為總水頭,h為壓力水頭,z為垂直坐標;C=?Se/?h為容水度,在非飽和區可表示為壓力水頭h或基質吸力s的函數,在飽和區為零,Se為飽和度;Ss為單位貯存量,在非飽和區為0;β在飽和區等于1,非飽和區等于0。
巖土體中的飽和/非飽和滲流規律可用廣義Darcy定律表示:
v=-kr(s)k▽φ
(2)
式中:k為巖土體的飽和滲透張量;kr為相對滲透率,可表示為飽和度Se或基質吸力s的函數。
式(1)的初始條件如下:
φ(x,y,z,t0)=φ0(x,y,z) (inΩ)
(3)
式中:φ0為初始水頭場;t0為初始時刻;x和y為坐標分量。
式(1)還應滿足如下邊界條件:
(1)水頭邊界條件:

(4)

(2)流量邊界條件:
(5)
(3)飽和溢出邊界條件:
qn=-v·n≤0 且φ=z(onΓs)
(6)
式中:Γs為溢出邊界。
(4)非飽和流量邊界條件:
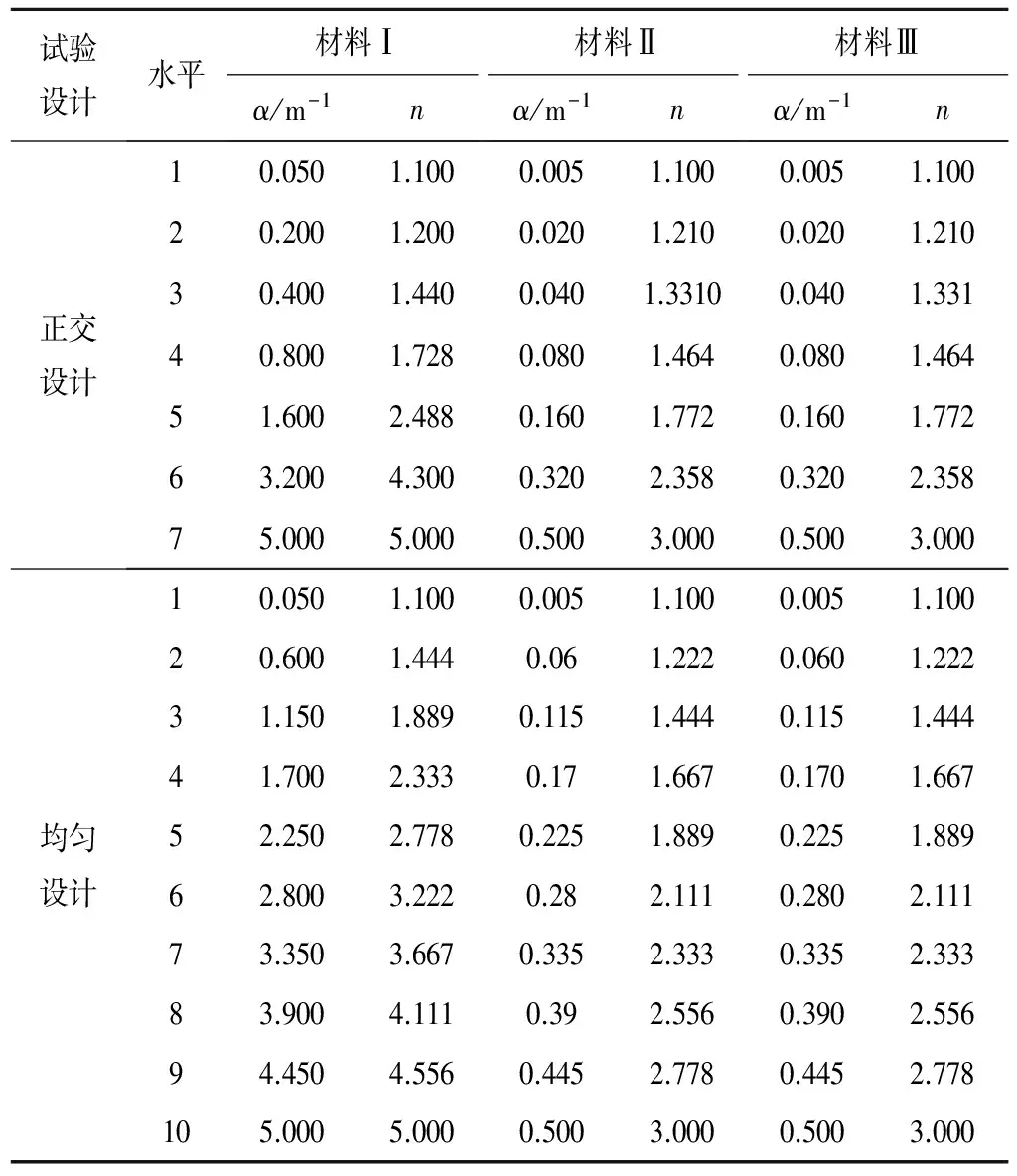
且φ (7) 式中:Γuq為非飽和流量邊界,包括溢出邊界ΓE(如蒸發邊界)和降雨入滲邊界ΓR。 巖土體飽和度Se與基質吸力s之間的關系稱為持水特性曲線。在眾多描述持水特征曲線的模型中,V-G模型以其線型與實測數據吻合程度高而得到廣泛應用[12],其表達式如下: (9) 式中:θ為巖土體體積含水率;θr、θs為巖土體殘余含水率和飽和含水率;α為反映巖體進氣值的參數,n為控制曲線斜率的參數,m=1-1/n。四個模型參數中,飽和含水率θs、殘余含水率θr與巖土體本身的性質及類型有關,可通過室內或現場試驗確定或根據巖土體孔隙率大致確定;而α和n則為經驗擬合參數,對非飽和滲流運動有顯著的影響[13]。因此,在非飽和滲流反演分析中,經驗參數α、n可作為待反演參數,來確定非飽和水力特征參數取值,進而描述非飽和滲流運動規律。 (10) 式中:f1(·)為目標函數;G與R為待反演非飽和參數與降雨數據;φki與φi為監測點i的實測數據與計算數據;‖·‖2與dim(·)分別表示歐幾里德范數與向量的維度。 由于采用試算方法確定待反演參數存在效率較低、耗時較長且容易陷入局部最優等問題,本文將正交設計、非飽和滲流正分析、BP神經網絡和遺傳算法相結合,以保證反演分析的可行性與有效性。反演分析流程圖如圖1所示。 圖1 反演分析方法流程圖Fig.1 Flow chart of back-analysis method 正交設計可以在眾多的試驗方案中安排少量有代表性的方案,采用正交設計科學安排神經網絡的訓練樣本數,可使反演分析計算量大為減少[14]。在實際工程反演問題中,計算規模一般較大,如需進行5水平6因素試驗時,若采用全面試驗,則要進行56=15 625次有限元正算,計算量巨大,若采用正交設計僅需36次計算即可滿足要求。 根據正交設計給出的一系列非飽和參數組合,采用前述非飽和滲流計算方法進行有限元計算,得到各個監測點的水頭數據,并以此作為BP神經網絡的訓練樣本。 BP神經網絡是按誤差逆傳播算法訓練的多層前饋網絡的簡稱,可以建立輸入數據與輸出數據之間的隱式映射關系[15,16]。 圖2 單隱含層BP網絡結構圖Fig.2 Structure of a typical single hidden-layer BPNN 圖2為單隱含層BP網絡結構圖,包括一個輸入層(Y),一個隱含層(Z)和一個輸出層(K),神經網絡的輸入層參數為巖土體非飽和參數組合和降雨數據,輸出層為監測點水頭數據。由于樣本數據量綱不同,在神經網絡訓練之前,需對根據下式對輸入和輸出數據進行歸一化預處理。 (11) 式中:pn歸一化后的值;p為樣本原始值;pmax和pmin分別為樣本原始的最大值和最小值。 BP神經網絡訓練步驟如下: (1)神經網絡中給每個連接權值和閾值賦位于區間(-1, 1 )上的隨機初始值。 (2)提供訓練輸入樣本和目標輸出樣本。 (3)隨機選取一個輸入樣本,計算BP神經網絡隱含層和輸出層各節點的輸出值。 (4)根據目標值與輸出值之間的偏差,計算反向誤差,對權值進行修正。 (5)選取下一個訓練樣本提供給神經網絡,返回步驟(3),直至整個訓練樣本訓練完畢。 (6)重復樣本學習,直至神經網絡的全局誤差E收斂至小于目標誤差,此時神經網絡訓練結束。 遺傳算法是一種仿生物全局優化算法,其靈感來自于自然選擇和進化過程,可以達到解的優化最大化。該算法克服了傳統方法易于陷入局部最優解的缺點,適用于目標函數具有多極值點的優化問題[17]。采用遺傳算法能夠找到一組監測點水位計算數據與實測數據最為吻合的參數組合,以此作為非飽和參數的最佳反演參數。遺傳算法的實施步驟如下: (1)種群初始化。在巖土體非飽和參數的取值范圍內,生成一系列隨機解,形成初始種群N,并對其進行二進制編碼。 (2)適應度函數的設定。本文把目標函數[式(10)]的導數值作為適應度函數,并把耗時的有限元計算用訓練好的BP神經網絡代替,進而使反演效率大為提高。 (3)選擇、交叉和變異。選擇操作采用隨機遍歷抽樣的方式選擇最優個體,交叉操作采用交叉概率pc對個體進行交叉操作,變異操作使用變異概率pm產生出另外新的變異個體。 (4)循環操作。循環調用選擇、交叉和變異操作不斷地產生新的種群個體,直至迭代過程收斂,此時的最優個體即為巖土體非飽和參數最佳取值。 以一次降雨過程中巖質邊坡非飽和滲流場的動態變化為例,驗證上述反演分析方法的有效性和可靠性。計算模型如圖3所示,降雨量數據如圖4所示,邊坡三種巖土材料的飽和滲透系數k、巖土體的飽和含水率θs、殘余含水率θr為已知,具體取值見表1。選取三種典型巖土體的α、n值作為材料非飽和參數的真實值。將多年平均降雨量(2 mm/d)對應的穩態滲流場作為初始條件進行非飽和滲流分析。以非飽和滲流正算獲得的監測點水頭值作為水位觀測值。 圖3 邊坡計算模型(單位:m)Fig.3 Calculation model of the slope 圖4 降雨量柱狀圖Fig.4 Rainfall histogram 編號材料滲透系數/(cm·s-1)θsθrα/m-1真實值取值范圍反演值相對誤差/%n真實值取值范圍反演值相對誤差/%Ⅰ覆蓋層8.00×10-30.320.060.100.050~5.00.09970.302.31.1~5.02.29590.18Ⅱ強風化巖層2.00×10-40.120.030.050.005~0.50.05000.001.61.1~3.01.59780.14Ⅲ弱風化巖層2.00×10-50.090.020.020.005~0.50.02094.501.41.1~3.01.40930.47 根據典型巖土的α、n真實值確定其可能的取值范圍,每個參數選取7個水平,如表2所示,采用正交設計方法安排49種參數組合。對每組方案進行有限元計算,得到各監測點的水位計算值數據。 表2 正交設計和均勻設計水平與因素表Tab.2 Factors and levels of orthogonal and even design 以上述49種非飽和參數組合方案和降雨數據為BP神經網絡的輸入,以每組方案下監測點的水位變動數據為BP神經網絡的輸出,得到BP神經網絡的學習樣本。然后采用均勻設計表U*10(108)[18]構造10組參數組合方案,得到BP神經網絡的測試樣本。 本文神經網絡的訓練在MATLAB平臺上實現。本文采用的trainlm函數作為神經網絡訓練函數,采用tansig函數作為神經網絡隱含層傳遞函數,采用purelin函數作為輸出層傳遞函數,以均方誤差函數mse作為網絡性能函數。神經網絡最大訓練次數為1 000次,目標誤差為0.001。初始的連接權值和閾值設置為默認值,學習率μ= 0.05,動量項系數η= 0.9。輸入層設為7個節點,輸出層設為4個節點。隱含層神經元根據試湊法確定[19],常用的經驗公式為: (12) 式中:z為隱含層節點數;y為輸入層節點數;k為輸出層節點數,p為1~10之間的整數。上式求得隱含層神經元個數為4~13個。通過試算,最終選用7-12-4神經網絡結構,此時測試樣本的均方誤差最小。圖5給出了7-12-4神經網絡結構下的誤差曲線,由圖可知,BP神經網絡在第27步達到目標誤差,此時的收斂誤差為0.000 435 6。 圖5 神經網絡訓練誤差曲線Fig.5 Neural network training error curve 根據2.2節所建立的目標函數[式(10)],采用遺傳優化算法尋找目標函數的最優解。本例的初始種群N的大小設置為50個,交叉pc和變異pm操作的概率分別為0.9和0.1,進化迭代過程見表3。由表3可見,隨迭代次數增加目標函數值不斷減小,且反演迭代過程穩定,在迭代步數達到16步時目標函數值僅為4.01 ×10-5,此時反演值與理論值已非常接近,說明本文方法是可行的。 監測點水位與反演計算值對比如圖6所示。由圖6可知,P1、P2測點位于強風化巖層,水位計算值與觀測值幾乎吻合,P3、P4測點位于弱風化巖層,監測點水位計算值與觀測值之間的誤差在0.2 m范圍內,表明本文方法是可靠的。 由表1可知,通過上述方法反演得到的三種材料的反演值與真實值極為相近,兩者相對誤差在5%以內。其中,覆蓋層和強風化巖層的反演結果尤為準確,這是由于覆蓋層、強風化巖層結構松散,降雨過程中非飽和帶水水分運動較快,因此該層的水位變動較大,非飽和參數α、n對降雨量及測點水位信息較為敏感;而弱風化巖層結構相對完整,該層地下水水位相對穩定,受上部降雨影響較小,反演結果有一定誤差。 表3 進化迭代過程Tab.3 Evolution iterating process 圖6 監測點水位與反演計算值對比圖Fig.6 Comparison of the measured and calculated water heads 本文根據監測點水位數據,將正交設計、非飽和滲流正分析、BP神經網絡、遺傳算法結合,提出了基于非穩定過程的巖土體非飽和參數反演分析方法,并通過算例驗證了該反演分析方法的有效性和可靠性,為現場條件下巖土體非飽和參數的確定提供了一種可行方案。 □ [1] 陳佩佩, 白 冰. 非飽和巖土介質滲流問題的光滑粒子法模擬[J]. 巖石力學與工程學報, 2016,35(10):2 124-2 130. [2] Fredlund D G,Xing A Q. Equations for the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994,31:521-532. [3] Fredlund D G,Huang X. Prediction the permeability functions for unsaturated soils using the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994,31:533-546. [4] Millington R J, Quirk J R. Permeability of porous solids[J]. Trans. Faraday Soc.,196157,(10):1 200-1 207 [5] Van Genuchten M T. A closed equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980,44:892-198. [6] 謝定義, 陳正漢. 非飽和土力學特性的理論與測試[C]∥ 土力學及基礎工程學會. 非飽和土理論與實踐學術研討會文集. 北京:1992:227-229. [7] 程金茹, 郭擇德, 郭大波. 非飽和土壤特性參數獲取方法[J]. 水文地質工程地質, 1996,(2):9-13. [8] 孫樹林, 王利豐. 非飽和裂隙孔隙巖體持水曲線的預測研究[J].巖石力學與工程學報, 2006,25:3 830-3 834. [9] 王恩志. 裂隙巖體非飽和滲流本構關系[J].巖石力學與工程學報, 2003,22(12):2 037-2 041. [10] 張乾飛, 王 建, 吳中如. 基于人工神經網絡的大壩滲透系數分區反演分析[J]. 水電能源科學, 2001,19(4):4-7. [11] 劉 杰, 王 媛. 改進的遺傳算法及其在滲流參數反演中的應用[J]. 巖土力學, 2003,24(2):237-241. [12] 徐紹輝, 張佳寶, 劉建立, 等. 表征土壤水分持留曲線的幾種模型的適應性研究[J]. 土壤學報, 2002,39(4):498-504. [13] 吳禮舟, 黃潤秋. 非飽和土滲流及其參數影響的數值分析[J]. 水文地質工程地質, 2011,38(1):94-98. [14] 陳益峰, 周創兵. 基于正交設計的復雜壩基彈塑性力學參數反演[J]. 巖土力學, 2002,23(4):450-454. [15] 周 喻, 吳順川, 焦建津,等. 基于BP神經網絡的巖土體細觀力學參數研究[J]. 巖土力學, 2011,32(12):3 821-3 826. [16] 吳云星, 王士軍, 谷艷昌, 等. 基于GA-LMBP神經網絡模型的大壩滲流壓力預報分析[J].水電能源科學, 2016,34(10):55-59. [17] GOLDBERG D E. Genetic algorithms in search, optimization and machine learning[M]. New York: Addison-Wesley, 1989:1-21. [18] 方開泰. 均勻設計與均勻設計表[M]. 北京: 科學出版社, 1994:69-97. [19] 韓力群. 人工神經網絡理論、設計及應用[M]. 北京: 化學出版社, 2007.1.2 非飽和滲流反問題

2 巖土體非飽和參數反演分析方法
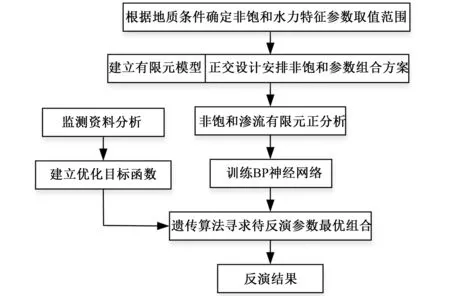
2.1 正交設計
2.2 非飽和滲流正分析
2.3 BP神經網絡

2.4 遺傳算法
3 算例驗證



3.1 正交設計與正分析
3.2 BP神經網絡模型構建

3.3 遺傳算法尋優
3.4 反演分析結果


4 結 論

