涪江橋流域雨量站網(wǎng)分布與面雨量誤差關(guān)系研究

程中陽，張行南,2,3

(1.河海大學(xué) 水文水資源學(xué)院，南京 210098；2.河海大學(xué)水安全與水科學(xué)協(xié)同創(chuàng)新中心，南京 210098；3.河海大學(xué)水資源高效利用與工程安全國(guó)家工程研究中心，南京 210098)

0 引 言

由于近年來全球氣候變化引起的極端降水事件的增加，水文部門對(duì)實(shí)時(shí)洪水預(yù)報(bào)的精度提出了越來越高的要求。面雨量作為洪水預(yù)報(bào)模型最重要的驅(qū)動(dòng)因子，其誤差直接決定模型產(chǎn)流量偏差，進(jìn)而影響洪水預(yù)報(bào)的精度[1,2]。

獲取流域面雨量傳統(tǒng)方法，主要由地面觀測(cè)站常規(guī)資料，采用面雨量估算方法推求。隨著科學(xué)技術(shù)水平的發(fā)展，雷達(dá)、衛(wèi)星等現(xiàn)代方法的使用愈來愈普遍[3]。尤其是雷達(dá)測(cè)雨，在實(shí)時(shí)作業(yè)預(yù)報(bào)中發(fā)揮著越來越重要的作用，但因其需要反演和標(biāo)定，其精度仍難以滿足水文業(yè)務(wù)的需求[4]。所以，水利部門進(jìn)行實(shí)時(shí)洪水預(yù)報(bào)采用的降水資料仍以常規(guī)雨量站監(jiān)測(cè)資料為主，因此雨量站網(wǎng)的分布情況會(huì)直接影響面雨量的估算結(jié)果。陳利群等[5]分析了雨量站密度對(duì)流域產(chǎn)流產(chǎn)沙的影響，發(fā)現(xiàn)站網(wǎng)密度與面雨量誤差呈反比關(guān)系。王國(guó)慶等[6]研究了站網(wǎng)密度對(duì)不同氣候區(qū)月水文過程模擬的影響，發(fā)現(xiàn)面雨量誤差對(duì)水文模擬的影響可以通過參數(shù)優(yōu)化的方式得到改善。蔚英華等[7]分析了不同地形條件下站網(wǎng)密度對(duì)面雨量精度的影響，發(fā)現(xiàn)站網(wǎng)密度對(duì)地形分布和降水分布差異明顯的地區(qū)影響最大。國(guó)內(nèi)學(xué)者對(duì)站網(wǎng)密度與面雨量精度關(guān)系研究逐漸深入，但對(duì)雨量站點(diǎn)分布均勻性、高程等與面雨量計(jì)算誤差之間的關(guān)系研究尚不成熟。

因此，本文以涪江橋流域?yàn)檠芯繀^(qū)域，利用抽站法原理，選取125種雨量站網(wǎng)分布，分析雨量站點(diǎn)密度、分布均勻度、高程對(duì)面雨量誤差的影響，為水文站網(wǎng)規(guī)劃、改進(jìn)降水插值方法、研究洪水預(yù)報(bào)模型輸入誤差提供科學(xué)依據(jù)。

1 研究區(qū)概況及面雨量計(jì)算方法

1.1 研究區(qū)概況

涪江是嘉陵江下游右岸最大支流，發(fā)源于四川省松潘縣岷山雪寶頂北麓，地形自西北向東南由山區(qū)逐漸變?yōu)榕璧厍鹆陞^(qū)，河長(zhǎng)697 km。涪江橋流域位于涪江中上游地區(qū)，地處31°29′N～32°33′N、103°42′E～105°00′E之間，流域面積7 570.6 km2，平均高程1 683 m。流域?qū)儆趤啛釒駶?rùn)性季風(fēng)氣候，雨量豐沛但時(shí)空差異較大。涪江橋流域多年平均流量280 m3/s，每年5月至10月為豐水期，占年水量的80.5%，11月至翌年4月為枯水期，占年水量的19.5%。涪江橋流域圖如圖1所示。

圖1 涪江橋流域圖Fig.1 The map of Fujiangqiao river basin

1.2 面雨量計(jì)算方法

面雨量估算方法主要有泰森多邊形法、算術(shù)平均法、等雨量線法和網(wǎng)格法等[8]。泰森多邊形法假設(shè)在兩個(gè)雨量站間降雨呈線性變化，從而將降雨空間分布概化成在多邊形邊界產(chǎn)生突變，而在多邊形內(nèi)均勻分布，分別計(jì)算各多邊形的面降雨[9]。算術(shù)平均法即以所有站點(diǎn)的降雨量的算術(shù)平均值作為計(jì)算區(qū)域的面雨量，計(jì)算簡(jiǎn)單是該方法的特點(diǎn)，但在站網(wǎng)分布稀疏，或分布不均勻的條件下，可能難以得到滿意的結(jié)果。等雨量線法是由點(diǎn)雨量繪制研究區(qū)雨量等值線圖，并假定兩等值線內(nèi)雨量呈線性分布，由等值線所圍面積計(jì)算面雨量，該方法具有較好的理論基礎(chǔ)，能反應(yīng)地形變化對(duì)降雨空間分布的影響，難點(diǎn)在于可靠的等值線繪制、計(jì)算方法相對(duì)復(fù)雜。網(wǎng)格法是由實(shí)測(cè)降雨資料通過空間插值得到網(wǎng)格點(diǎn)的雨量，再求出流域內(nèi)包含的網(wǎng)格點(diǎn)的降雨量的平均值得到流域面雨量，該方法具有較強(qiáng)的理論基礎(chǔ)，方法原理簡(jiǎn)單，操作簡(jiǎn)便，對(duì)監(jiān)測(cè)站點(diǎn)空間分布依賴性不強(qiáng)。本項(xiàng)目研究的是遙測(cè)站網(wǎng)監(jiān)測(cè)的雨量數(shù)據(jù)，相對(duì)來說站點(diǎn)較密，但站點(diǎn)空間分布的合理性和科學(xué)性的驗(yàn)證有所欠缺。為此，本項(xiàng)目選擇對(duì)站網(wǎng)空間分布依賴性較弱，且計(jì)算方法相對(duì)簡(jiǎn)單，易于實(shí)現(xiàn)標(biāo)準(zhǔn)化計(jì)算的網(wǎng)格法來計(jì)算面雨量。

網(wǎng)格法計(jì)算，涉及空間插值方法的選用，最常用的是反距離權(quán)重法。反距離權(quán)重法理論依據(jù)為“地學(xué)第一定律”，即距離越近的觀察點(diǎn)對(duì)待估計(jì)點(diǎn)的影響越大，各網(wǎng)格點(diǎn)處的雨量 可以通過附近一定范圍內(nèi)的雨量站實(shí)測(cè)資料通過加權(quán)平均求得，公式如下：

(1)

式中：xj指第j個(gè)網(wǎng)格處待估點(diǎn)的降雨量；m指第j個(gè)網(wǎng)格處附近的雨量站個(gè)數(shù)；xi指第j個(gè)網(wǎng)格處附近第i個(gè)雨量站實(shí)測(cè)降雨量；di指第j個(gè)網(wǎng)格處到附近第i個(gè)雨量站的距離；p指距離的冪，通常取2。

1.3 技術(shù)路線

本文選用涪江橋流域2007年日降水資料。具體研究技術(shù)路線如圖2所示。

圖2 技術(shù)路線Fig.2 The technical route

2 計(jì)算過程及關(guān)系分析

2.1 計(jì)算雨量站確定

在計(jì)算流域面雨量時(shí)，常常只用到流域內(nèi)部的雨量站的數(shù)據(jù)，這樣會(huì)造成降水插值結(jié)果的“邊界效應(yīng)”[10]，即流域外圍插值結(jié)果準(zhǔn)確性不高。因此，考慮一定的緩沖區(qū)，一方面，減小降水插值邊界誤差，另一方面，用緩沖區(qū)內(nèi)的所有站點(diǎn)進(jìn)行降水空間插值，計(jì)算出的面雨量作為近似真值，為后續(xù)研究奠定基礎(chǔ)。利用涪江橋流域的降水影響范圍確定緩沖區(qū)半徑，該流域降水影響范圍的確定方法是：作不同雨量站點(diǎn)之間降水量皮爾遜相關(guān)系數(shù)和站點(diǎn)距離的散點(diǎn)圖(如圖3所示)，確定緩沖半徑。

皮爾遜相關(guān)系數(shù)也叫簡(jiǎn)單相關(guān)系數(shù)，是度量?jī)蓚€(gè)變量相關(guān)程度的統(tǒng)計(jì)變量，公式如下：

(2)

式中：X、Y表示不同站點(diǎn)的降水?dāng)?shù)據(jù)系列；N表示降水系列的個(gè)數(shù)。

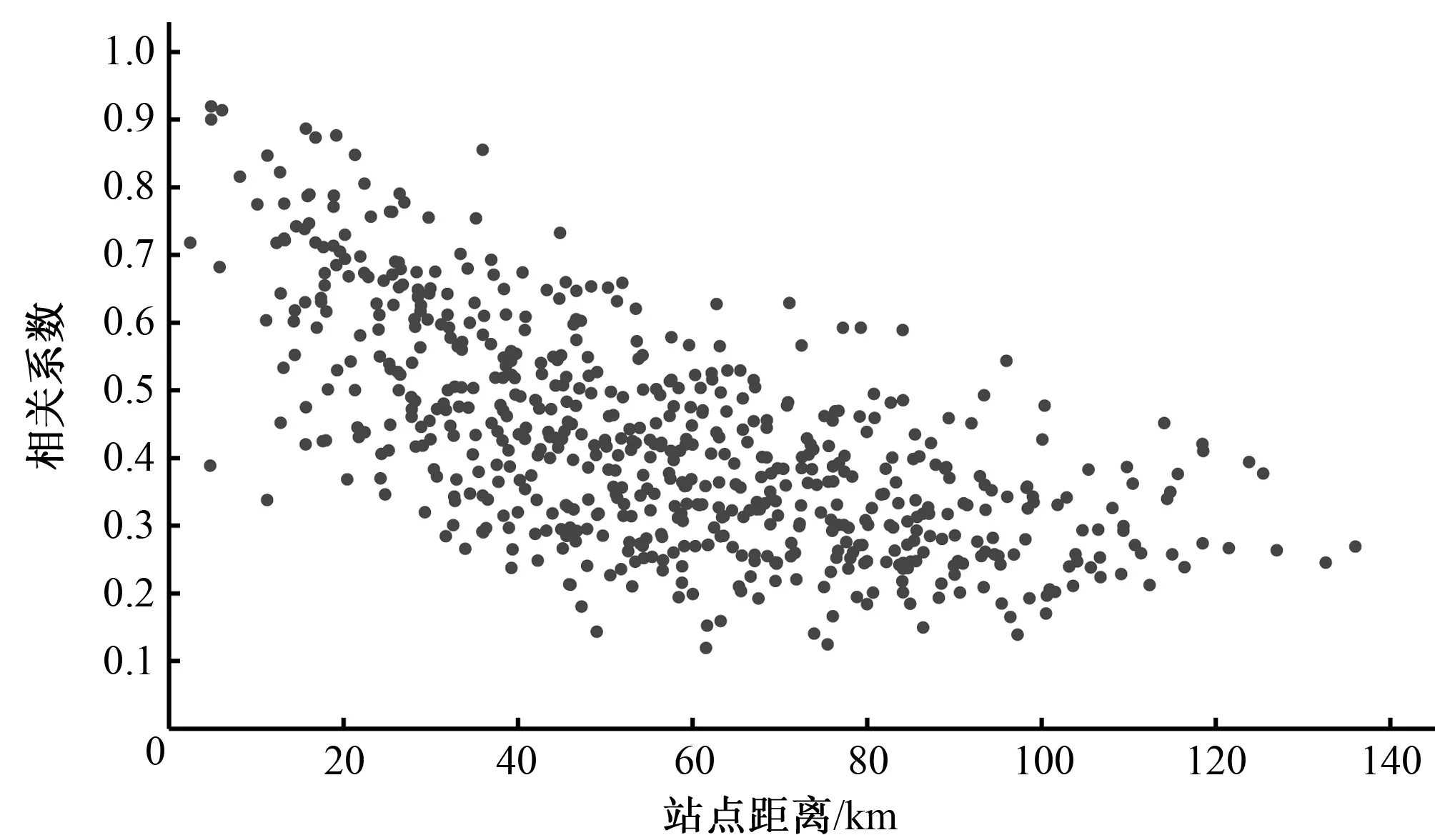
圖3 相關(guān)系數(shù)和站點(diǎn)距離關(guān)系圖Fig.3 The relationship between the correlation coefficient and the rainfall station distance

由圖3可知，雨量站之間降雨數(shù)據(jù)的相關(guān)系數(shù)隨站點(diǎn)距離的增大呈明顯的減小趨勢(shì)，當(dāng)站點(diǎn)距離為20 km以上時(shí)，相關(guān)系數(shù)基本在0.7以下，說明當(dāng)雨量站點(diǎn)距離大于20 km時(shí)，兩地的降雨相關(guān)性較弱。因此，涪江橋流域的緩沖半徑設(shè)為20 km，該范圍內(nèi)參與插值計(jì)算的雨量站共有36個(gè)。

2.2 確定站網(wǎng)分布

在站網(wǎng)規(guī)劃中，常利用抽站法研究站網(wǎng)布設(shè)合理性。一般將站網(wǎng)稠密地區(qū)的全部降雨資料計(jì)算的面雨量作為面雨量近似真值，然后按照分布均勻的抽站原則抽去一部分雨量站，再計(jì)算面雨量及其誤差，尋求誤差與布站密度的關(guān)系[11]。

為研究面雨量計(jì)算結(jié)果與站點(diǎn)分布的關(guān)系，借鑒抽站法原理，利用涪江橋流域36個(gè)雨量站點(diǎn)的資料計(jì)算的面雨量作為面雨量近似真值，然后利用隨機(jī)抽樣的原理，按照30、24、18、12、6站的數(shù)量抽取雨量站點(diǎn)，各抽取25次，組成125種站網(wǎng)分布，對(duì)每種站網(wǎng)分布進(jìn)行插值，計(jì)算面雨量，然后將不同站網(wǎng)分布下的面雨量作為理論值，統(tǒng)計(jì)近似真值與理論值之間的誤差，研究誤差與站網(wǎng)分布的關(guān)系。

2.3 均勻度計(jì)算

雨量站網(wǎng)分布合理性評(píng)價(jià)可包括幾個(gè)方面：站網(wǎng)密度、站網(wǎng)分布均勻性、站點(diǎn)高程分布等。為研究面雨量誤差與站網(wǎng)分布均勻性的關(guān)系，引入站網(wǎng)分布均勻度指標(biāo)描述站點(diǎn)分布情況。在涪江橋流域緩沖區(qū)內(nèi)，對(duì)上述確定的125種站網(wǎng)，利用泰森多邊形法計(jì)算每站的控制面積，用下式計(jì)算站網(wǎng)分布均勻度：

(3)

式中：E為站網(wǎng)分布均勻度；fi為第i個(gè)雨量站的控制面積；f為雨量站控制面積的平均值；F為流域總面積；n為雨量站個(gè)數(shù)。

2.4 面雨量計(jì)算誤差統(tǒng)計(jì)

在進(jìn)行誤差計(jì)算時(shí)還涉及一個(gè)關(guān)鍵問題，是否統(tǒng)計(jì)整個(gè)流域的面雨量誤差還是分區(qū)統(tǒng)計(jì)。實(shí)際應(yīng)用中，常常關(guān)心整個(gè)流域的面雨量大小和面雨量在流域內(nèi)的分布情況。并且，在流域水文模擬和實(shí)時(shí)洪水預(yù)報(bào)中，以我國(guó)最具世界影響力的新安江模型為例，該模型考慮了流域下墊面水文特性的空間差異，把流域離散成多個(gè)子單元進(jìn)行降雨徑流模擬，將子單元的面雨量作為模型的輸入。因此，本文依據(jù)這一思想，采用自然流域分塊的方法，將涪江橋流域劃分成21個(gè)子單元，分別統(tǒng)計(jì)子單元和全流域面雨量誤差，探究面雨量誤差和與站網(wǎng)分布的關(guān)系。

研究選用平均絕對(duì)誤差和均方差度量面雨量誤差。平均絕對(duì)誤差(Mean Absolute Error，MAE)反映了理論值偏離真實(shí)值的大小，給出了可能的誤差范圍。均方差(Mean Square Error，MSE)反映了利用實(shí)測(cè)站點(diǎn)數(shù)據(jù)計(jì)算面雨量的靈敏度，估計(jì)了理論值與真實(shí)值系列的擬合程度。二者的計(jì)算公式如下：

(5)

式中：Pc為面雨量理論值；Po為面雨量真值；n為降雨系列個(gè)數(shù)。

此外，本文利用面雨量點(diǎn)面系數(shù)側(cè)面反映站網(wǎng)分布與面雨量精度關(guān)系。面雨量點(diǎn)面關(guān)系系數(shù)ric是指在面積A上，任一站點(diǎn)雨量序列與面雨量序列的相關(guān)程度，反映了降雨隨機(jī)場(chǎng)的局部與整體之間的關(guān)系。

(6)

2.5 關(guān)系分析

2.5.1 面雨量誤差與站網(wǎng)密度關(guān)系

統(tǒng)計(jì)5組站網(wǎng)密度下的面雨量平均絕對(duì)誤差與均方差，作站點(diǎn)個(gè)數(shù)與誤差關(guān)系圖(如圖4)，可以發(fā)現(xiàn)，站網(wǎng)密度對(duì)面雨量誤差有顯著影響，雨量站數(shù)量的多寡對(duì)子單元和全流域面雨量誤差的影響趨勢(shì)一致。當(dāng)參與面雨量計(jì)算的站點(diǎn)個(gè)數(shù)由30個(gè)減為24個(gè)時(shí)，站網(wǎng)密度變化對(duì)面雨量誤差大小幾乎沒有影響，但當(dāng)雨量站數(shù)量少于24個(gè)時(shí)，子單元和全流域的面雨量平均絕對(duì)誤差和均方差隨站點(diǎn)個(gè)數(shù)的減少呈明顯的增大趨勢(shì)，且增大速率也呈一定規(guī)律。經(jīng)計(jì)算發(fā)現(xiàn)，子單元和全流域的平均絕對(duì)誤差和均方差隨雨量站數(shù)量的減少，其增大速率呈先增加后減小的趨勢(shì)，站點(diǎn)個(gè)數(shù)由18個(gè)站減小到12個(gè)站時(shí)，誤差增大幅度最大，說明站點(diǎn)個(gè)數(shù)減為12時(shí)，無論站點(diǎn)如何分布，都很難捕捉較為準(zhǔn)確的降雨空間分布信息，站點(diǎn)由12個(gè)站減小到6個(gè)站時(shí)，誤差增大幅度有所回落。且流域MAE和MSE值的增大速率比子單元大，說明全流域面雨量誤差對(duì)站網(wǎng)密度變化的靈敏度更高。此外，子單元的誤差值大于相對(duì)應(yīng)的全流域誤差值，這是因?yàn)椋炅空痉植嫉南∈枧c稠密程度對(duì)面雨量精度的影響在局部統(tǒng)計(jì)中被放大了，在全流域統(tǒng)計(jì)時(shí)，局部偏差可以相互抵消，故誤差較小。

此外，從站點(diǎn)個(gè)數(shù)為6個(gè)站和30個(gè)站的站網(wǎng)分布中，各隨機(jī)挑選一種分布，計(jì)算這兩種站網(wǎng)分布下的面雨量點(diǎn)面相關(guān)系數(shù)，并作點(diǎn)面相關(guān)系數(shù)分布圖(如圖5所示)。當(dāng)站點(diǎn)個(gè)數(shù)為6時(shí)，涪江橋流域北部和南部相關(guān)系數(shù)較高，但流域內(nèi)部相關(guān)系數(shù)較低；當(dāng)站點(diǎn)個(gè)數(shù)為30時(shí)，涪江橋流域大部分地區(qū)局部與整體之間的相關(guān)系數(shù)更高，結(jié)合此前分析，進(jìn)一步說明站網(wǎng)密度較大時(shí)，能比較準(zhǔn)確的反映空間降水情況，面雨量精度明顯提高。

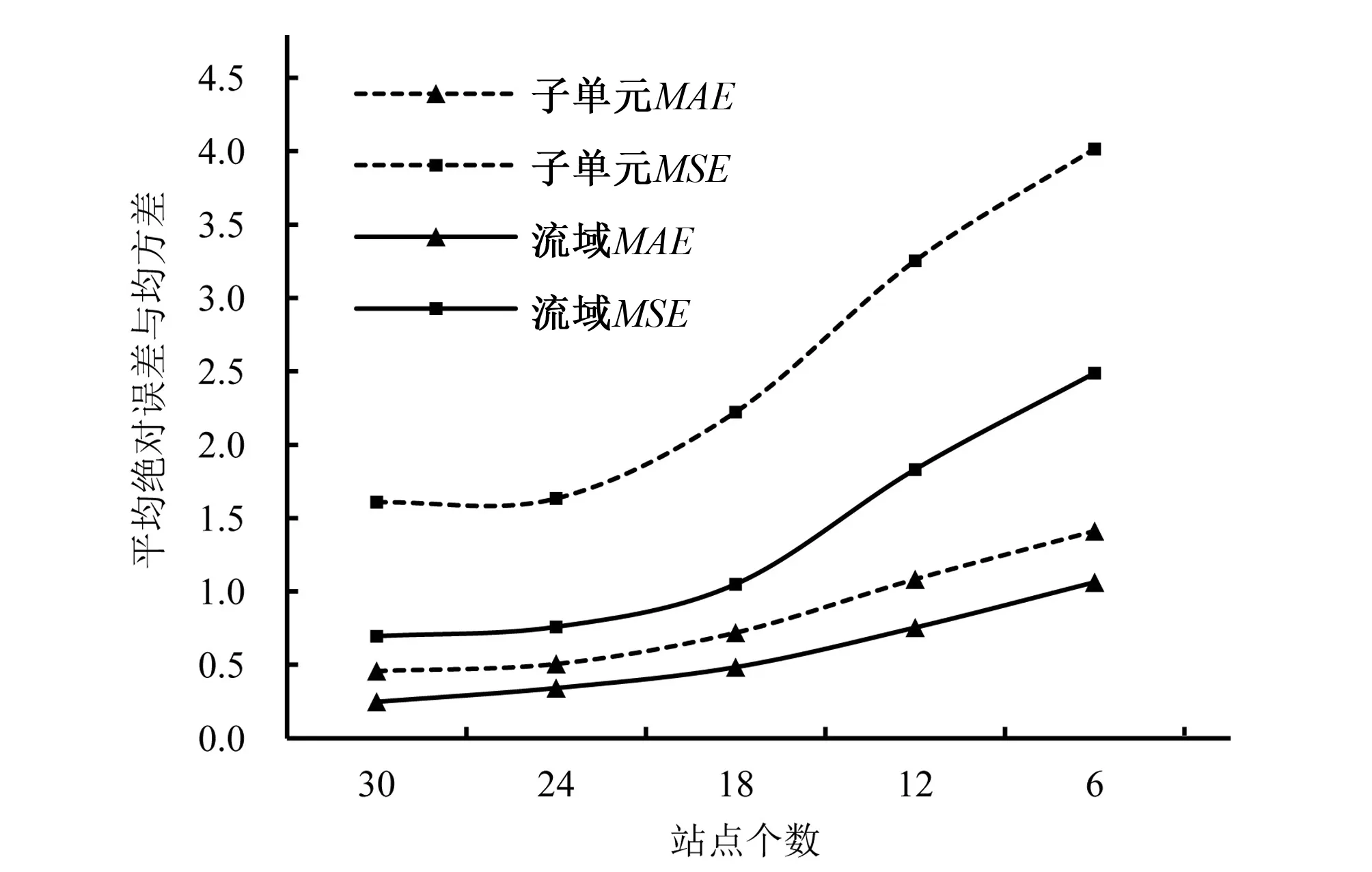
圖4 站網(wǎng)密度與面雨量誤差關(guān)系圖Fig.4 The relationship between the rainfall station network density and areal rainfall error

圖5 6個(gè)站與30個(gè)站點(diǎn)面相關(guān)系數(shù)分布Fig.5 The distribution of point and area correlation coefficient of 6 stations and 30 stations

2.5.2 面雨量誤差與均勻度關(guān)系

統(tǒng)計(jì)125種站網(wǎng)分布的均勻度、MAE、MSE，作不同站網(wǎng)密度下的均勻度與MAE、MSE的關(guān)系圖，因均勻度與MAE、MSE的關(guān)系一致，故以MAE為例進(jìn)行關(guān)系分析。

如圖6(a)～(e)所示，按照5組站網(wǎng)密度，分別統(tǒng)計(jì)其組內(nèi)25種站網(wǎng)分布均勻度與MAE關(guān)系，發(fā)現(xiàn)MAE隨均勻度的增大呈減小趨勢(shì)，說明站網(wǎng)分布越趨于均勻化，即站網(wǎng)分布均勻度越接近1，其計(jì)算的面雨量越合理。此外，站點(diǎn)數(shù)量較多時(shí)，圖中點(diǎn)據(jù)較密集，統(tǒng)計(jì)的平均絕對(duì)誤差較小，隨著站點(diǎn)數(shù)量的減少，圖6中點(diǎn)據(jù)較分散，統(tǒng)計(jì)的平均絕對(duì)誤差越大，計(jì)算的均勻度的最小值越小，說明站點(diǎn)數(shù)量較多時(shí)，站網(wǎng)分布均勻度對(duì)MAE極差的影響較小，即站網(wǎng)密度較大時(shí)，均勻度對(duì)面雨量誤差波動(dòng)范圍影響較小，站點(diǎn)數(shù)量較少時(shí)，站網(wǎng)分布均勻度對(duì)MAE極差的影響較大，此時(shí)均勻度對(duì)面雨量誤差波動(dòng)范圍影響較大，雖然分布較均勻可以降低面雨量誤差，但因插值所利用的實(shí)測(cè)資料太少，難以描述準(zhǔn)確的降雨空間分布，計(jì)算的面雨量誤差值仍較大。

作站點(diǎn)分布與子單元面雨量平均絕對(duì)誤差分布圖，可以更直觀地理解以上分析。圖7表示雨量站個(gè)數(shù)為30情況下，均勻度為0.969 7(a)和均勻度為0.972 5(b)的兩種站網(wǎng)分布，這兩種站網(wǎng)分布下的子單元MAE平均值分別為0.313 8和0.281 3。可以發(fā)現(xiàn)，站點(diǎn)較密集時(shí)，均勻度對(duì)面雨量誤差的影響較小，主要影響其在流域內(nèi)部的分布。圖8表示雨量站個(gè)數(shù)為6情況下，均勻度為0.918 4(a)和均勻度為0.880 6(b)的兩種站網(wǎng)分布，這兩種站網(wǎng)分布的子單元MAE平均值分別為1.312 8和1.077 6，圖8(a)站點(diǎn)在流域內(nèi)分布較均勻，只有2個(gè)子單元MAE值較大，圖8(b)站點(diǎn)則集中于流域東南部，西北部6個(gè)子單元MAE值都較大，站點(diǎn)較少時(shí)，均勻度對(duì)面雨量誤差的分布和統(tǒng)計(jì)值影響都較大。

統(tǒng)計(jì)所有站點(diǎn)均勻度與MAE的關(guān)系，如圖6(f)所示，發(fā)現(xiàn)子單元和全流域面雨量平均絕對(duì)誤差隨均勻度的增加而減小，基于以上分析，造成這一現(xiàn)象的原因有兩點(diǎn)，一是站網(wǎng)密度，二是均勻度。

2.5.3 面雨量誤差與雨量站高程關(guān)系

雨量站在流域內(nèi)的布設(shè)位置影響面雨量計(jì)算結(jié)果，統(tǒng)計(jì)125種站網(wǎng)分布的雨量站平均高程，并對(duì)站網(wǎng)平均高程以20 m為間隔劃分區(qū)間，統(tǒng)計(jì)每個(gè)站網(wǎng)平均高程區(qū)間內(nèi)的子單元和流域MAE值，如表2所示。

結(jié)果表明，子單元和全流域面雨量平均絕對(duì)誤差隨站網(wǎng)平均高程的增加而減小，說明站網(wǎng)平均高程越小，計(jì)算的面雨量誤差越大。這是因?yàn)椋⒔瓨蛄饔虻匦纹鸱容^大，北部為山區(qū)，南部為丘陵盆地，若站網(wǎng)平均高程較低，說明站點(diǎn)集中于中南部，對(duì)北部降雨插值計(jì)算結(jié)果不確定性較大；同理，若站點(diǎn)集中于北部山區(qū)，則計(jì)算結(jié)果的誤差也較大，但在實(shí)際布設(shè)站網(wǎng)的時(shí)候，因山區(qū)地形復(fù)雜陡峭，往往對(duì)水文觀測(cè)站的建立造成較大的困難，因此常出現(xiàn)站網(wǎng)平均高程偏低的情況。只有在流域內(nèi)站點(diǎn)充足的前提下，站網(wǎng)平均高程與流域平均高程接近時(shí)，計(jì)算的面雨量才更可靠。

3 結(jié)果與討論

(1)站網(wǎng)密度對(duì)面雨量計(jì)算精度有顯著影響，站網(wǎng)密度較大時(shí)，流域內(nèi)點(diǎn)面相關(guān)系數(shù)較高，能較準(zhǔn)確的反映空間降水情況。站點(diǎn)多與少對(duì)子單元和全流域面雨量誤差影響趨勢(shì)一致，全流域面雨量誤差對(duì)站網(wǎng)密度變化的靈敏度更高，且子單元誤差值大于全流域誤差值，站網(wǎng)密度增大到一定程度時(shí)，面雨量誤差變化趨于平緩。

圖6 站點(diǎn)分布均勻度與面雨量誤差關(guān)系圖Fig.6 The relationship between evenness and areal rainfall error

圖7 30站點(diǎn)分布與子單元面雨量平均絕對(duì)誤差分布圖Fig.7 The distribution of sub-basin areal rainfall mean absolute error of 30 stations

圖8 6站點(diǎn)分布與子單元面雨量平均絕對(duì)誤差分布圖Fig.8 The distribution of sub-basin areal rainfall mean absolute error of 6 stations

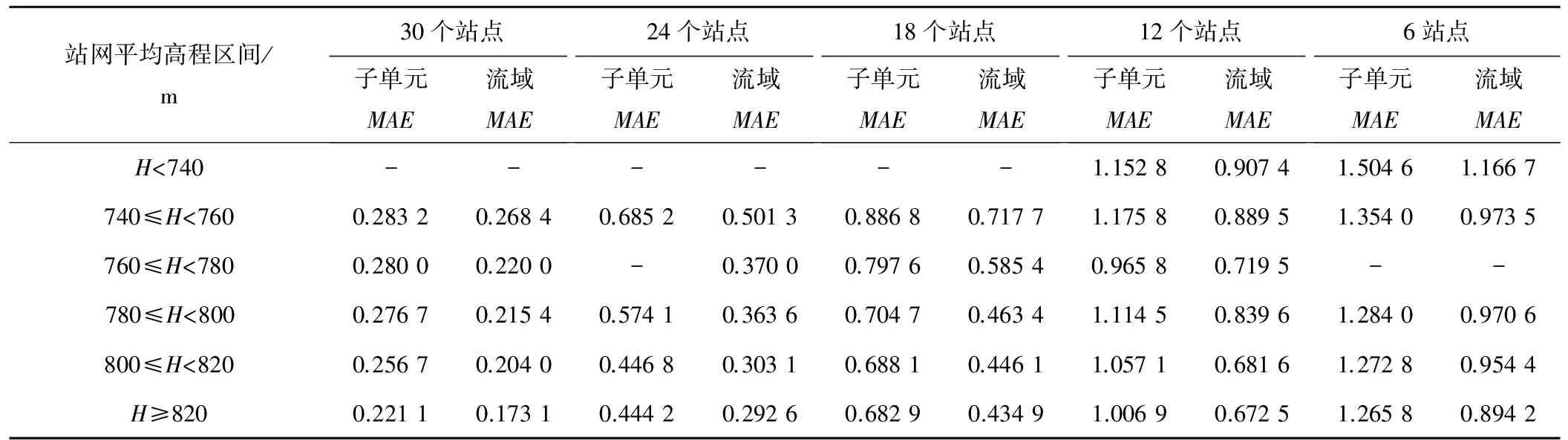
表2 面雨量誤差與站網(wǎng)平均高程關(guān)系Tab.2 The relationship between areal rainfall error and rainfall station network average elevation

(2)在同一站網(wǎng)密度下，均勻度越大，站網(wǎng)在流域內(nèi)分布越均勻，面雨量誤差值越小。站網(wǎng)密度較大時(shí)，均勻度對(duì)面雨量誤差波動(dòng)范圍的影響較小，主要影響其在流域內(nèi)部的分布；站網(wǎng)密度較小時(shí)，均勻度對(duì)面雨量誤差波動(dòng)范圍影響較大。

(3)子單元和全流域面雨量平均絕對(duì)誤差隨站網(wǎng)平均高程的增加而減小，只有流域站網(wǎng)密度較大，站網(wǎng)平均高程與流域平均高程接近時(shí)，計(jì)算的面雨量才更可靠。

□

[1] Chua S H, Bras R L. Optimal estimators of mean areal precipitation in regions of orographic influence[J]. Journal of Hydrology, 1982,57(1):23-48.

[2] 史曉亮, 楊志勇, 緒正瑞,等. 降雨輸入不確定性對(duì)分布式流域水文模擬的影響研究----以武烈河流域?yàn)槔齕J]. 水文, 2014, 34(6):26-32.

[3] 徐 晶, 姚學(xué)祥. 流域面雨量估算技術(shù)綜述[J]. 氣象, 2007,33(7):15-21.

[4] Alemohammad S H, Mccoll K A, Konings A G, et al. Characterization of precipitation product errors across the US using multiplicative Triple Collocation[J]. Hydrology & Earth System Sciences, 2015,12(2):2 527-2 559.

[5] 陳利群, 劉昌明, 郝芳華. 站網(wǎng)密度和地形對(duì)模擬產(chǎn)流量和產(chǎn)沙量的影響[J]. 水土保持學(xué)報(bào), 2005,19(1):18-21.

[6] 王國(guó)慶, 張建云, 張 明,等. 雨量站網(wǎng)密度對(duì)不同氣候區(qū)月徑流模擬的影響[J]. 人民長(zhǎng)江, 2009,40(8):45-49.

[7] 尉英華, 東高紅, 徐 姝. 海河流域不同地形站網(wǎng)密度對(duì)面雨量精度的影響[J]. 氣象與環(huán)境學(xué)報(bào), 2014,(6):75-79.

[8] 張行南, 程曉紅. 網(wǎng)格法在流域面雨量計(jì)算中的應(yīng)用研究[J]. 東北水利水電, 2005,22(5):16-17.

[9] 石 朋, 芮孝芳. 降雨空間插值方法的比較與改進(jìn)[J]. 河海大學(xué)學(xué)報(bào)自然科學(xué)版, 2005,33(4):361-365.

[11] 潘久根. 小流域雨量站網(wǎng)密度分析[J]. 四川大學(xué)學(xué)報(bào)(工程科學(xué)版), 1998,(2):29-33.