不同水熱條件下土壤累積氨揮發模型對比研究
馮 玚,郭向紅,孫西歡,馬娟娟,雷 濤,王宏宇
(太原理工大學水利科學與工程學院,太原 030024)
氨揮發是土壤氮素氣態損失的重要途徑,其損失量有時高達施氮量的40%~50%[1]。大氣中NH3濃度上升將導致酸沉降增多,從而引發酸雨、土壤酸化和水體富營養化等一系列生態環境問題[2-3],此外NH3還會引發溫室效應[4]。因此,開展不同水熱條件下土壤氨揮發定量研究,對于提高氮素利用效率、減少環境污染、構建生態農業等方面具有重要的作用和意義。
氨揮發是一個錯綜復雜的化學反應過程,常受到土壤狀況(質地、pH及肥力條件等)[5]、環境因子[6-7](溫濕度、風速及降雨等)和管理措施[8-9](施肥、灌溉及耕作方案)等諸多因素的影響。圍繞這些因素,國內外學者開展了大量的研究,并建立了Elovich等傳統的數學模型,而傳統的經驗模型很難保證其預測精度,為了提升模型性能,有必要創建模擬精度更高的數學模型。BP神經網絡是近幾年來迅速發展的人工智能新技術,它的靈活性比較大,具有很好的泛化能力和較強的容錯性,以及很強的非線性映射能力。但是在在實際應用中,BP神經網絡也暴露出一些自身的弱點,比如收斂速度慢、網絡極易陷入局部極值點;另外神經網絡的初始權值,閥值以及網絡結構的選擇缺乏依據,具有很大的隨機性,很難選取出具有全局性的初始點,因而求得全局最優的可能性較小。這些缺陷影響了BP神經網絡的泛化能力,限制了它在實際預測中的廣泛應用。遺傳算法是一種啟發式搜索算法,能夠避開局部極小點,而且在進化過程中也無需提供所要解決問題的梯度信息,具有較強魯棒性,隱含并行性和全局搜索特性[10]。因此,本文的目標為依據室內土壤氨揮發試驗資料,建立以溫度、水分和時間為輸入因子,氨揮發含量為輸出因子的BP神經網絡預測模型、GABP模型和Elovich模型,并對三種模型的預測效果進行比較,以期為土壤氨揮發研究提供精確的定量工具。
1 材料與方法
1.1 試驗材料
土壤樣本取自山西省太谷縣具有代表性的土壤,取土深度為0~200 cm,均為人工混合的組合樣品。取土時去除地表枯枝落葉,剔除土樣中的石塊、動植物殘渣等,放置陰涼處待自然風干后,過2 mm篩后備用。風干土壤基本性質為:質地為沙壤土,含水率31.0 g/kg,田間持水量0.217 g/g,硝態氮含量4 mg/kg,銨態氨含量6 mg/kg,容重1.47 g/cm3。
1.2 試驗設計
本試驗采用室內培養法,進行不同含水量、溫度條件下土壤氨揮發試驗研究。土壤含水量分別設置為田間持水量的60%、80%和100%三個水平。培養溫度分別設15、25和35 ℃三個水平。采用全面試驗設計,共9個處理。每日采用精度為0.01 g的電子天平,利用稱重法對損失的水分進行及時補充,使含水量保持在試驗設定值。試驗開始后將各個處理的燒杯分別放進SPX-BE系列恒溫箱(精度0.1 ℃)中持續培養15天。試驗通過磷酸甘油雙層海綿通氣法來進行氨氣的收集,將兩塊涂抹有15 mL磷酸甘油溶液(5∶4)的海綿放入下次要采樣的燒杯中,下方海綿用來吸收土壤釋放的氨氣,上方海綿吸收大氣中的氨氣,防止其進入燒杯內,影響試驗精度。于試驗開始后的奇數天采樣,取樣時,下方的海綿剪成2個30°的對角,剪碎裝入250 mL的錐形瓶中,并加入濃度為1.0 mol/ L的100 mLKCl溶液,以便海綿可以完全浸于其中,之后利用振蕩器振蕩1h,過濾,提取最后要測定的溶液,浸取液中的銨態氮用連續流動分析儀測定。
1.3 模型建立
(1)Elovich模型:首先按時間序列建立Elovich數學模型進行氨揮發的動力學研究,定量描述土壤的氨揮發過程。Elovich模型的方程為:
(1)
式中:t為培養時間;y為氨揮發量;c為常數;K為氨揮發速率即為單位時間內的氨揮發量。
(2)BP神經網絡:本研究結合前人研究成果以及多種隱含層節點計算的經驗公式,經過對不同隱含層節點數的多次試算后,確定隱含層節點數為5時,可達到最優模擬效果,因此,本文的BP神經網絡拓撲結構確定為3-5-1。其中,輸入層包括三項,分別為時間、含水量、溫度,輸出層為氨揮發含量。不同水熱條件下的氨揮發數據集中,三種溫度、三種含水量處理下的7 d數據共63個,以6∶1的比例進行分配,分別作為訓練集和檢驗集,兩者的樣本數分別為54和9。網絡中間層和輸出層的神經元傳遞函數分別為雙曲正切函數及恒等函數。優化算法和訓練目標誤差分別為共軛梯度法和0.000 1。
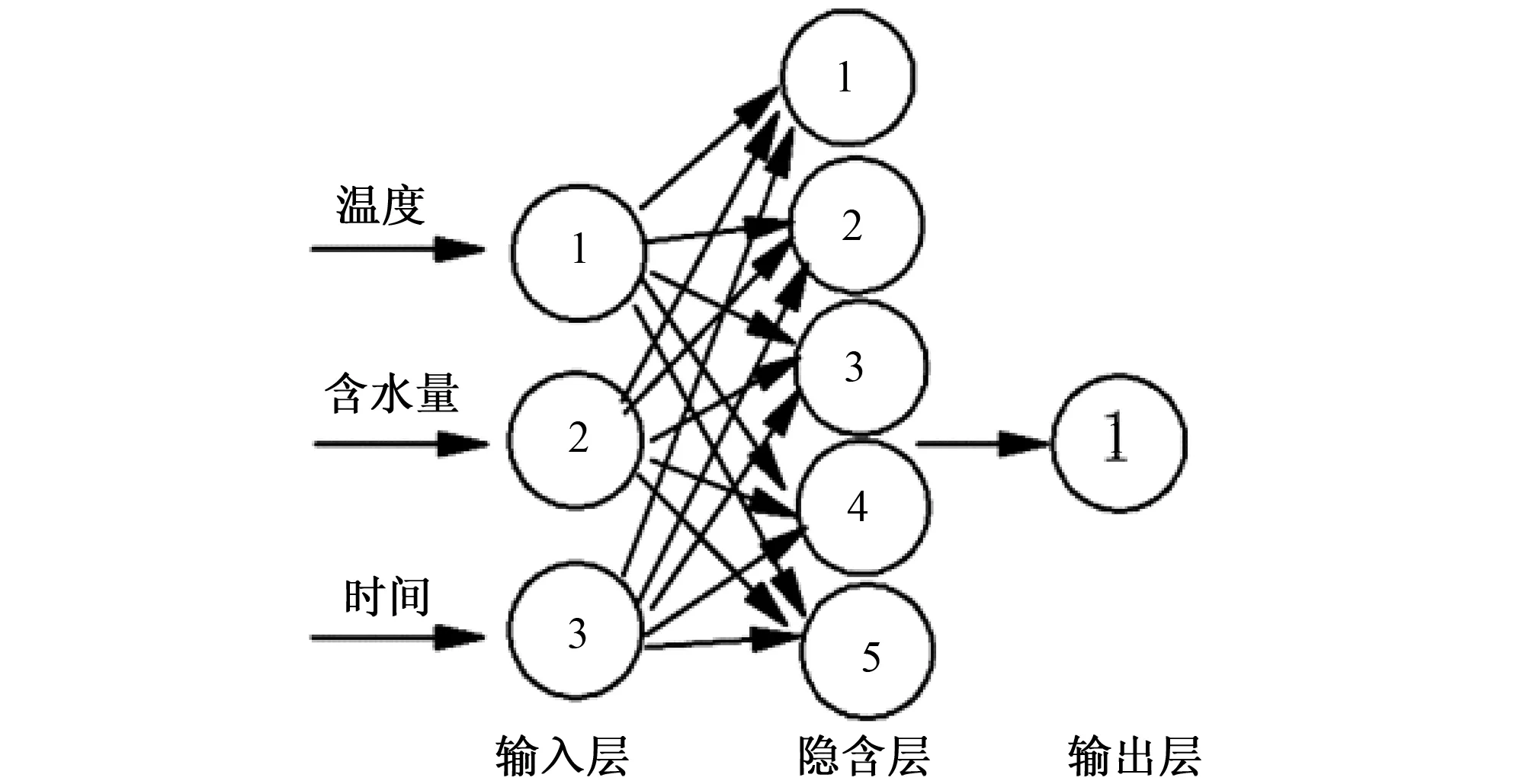
圖1 氨揮發BP神經網絡模型結構圖Fig.1Architecture of the BP neural network of ammonia
(3)GABP網絡:圖2為GABP神經網絡模型流程圖,在BP神經網絡模擬模塊,具體的拓撲結構與參數設置均與單純的BP神經網絡算法相同,在遺傳算法部分,對BP神經網絡權值、閾值進行優化,從而提高神經網絡的擬合效果。其中,遺傳算法的具體參數設置如下:迭代次數為10,種群規模為50,交叉概率為0.7,變異概率為0.001。
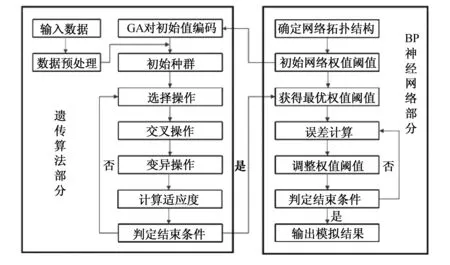
圖2 GABP模型流程圖Fig.2 Algorithm process of the GABP neural network
1.4 模型評價指標
對模型預測性能的評價指標包括:決定系數R2,平均相對誤差MAPE,相關系數r,其計算公式如下:
(2)
(4)
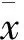
2 結果分析
2.1 不同處理下土壤氨揮發動力學特性
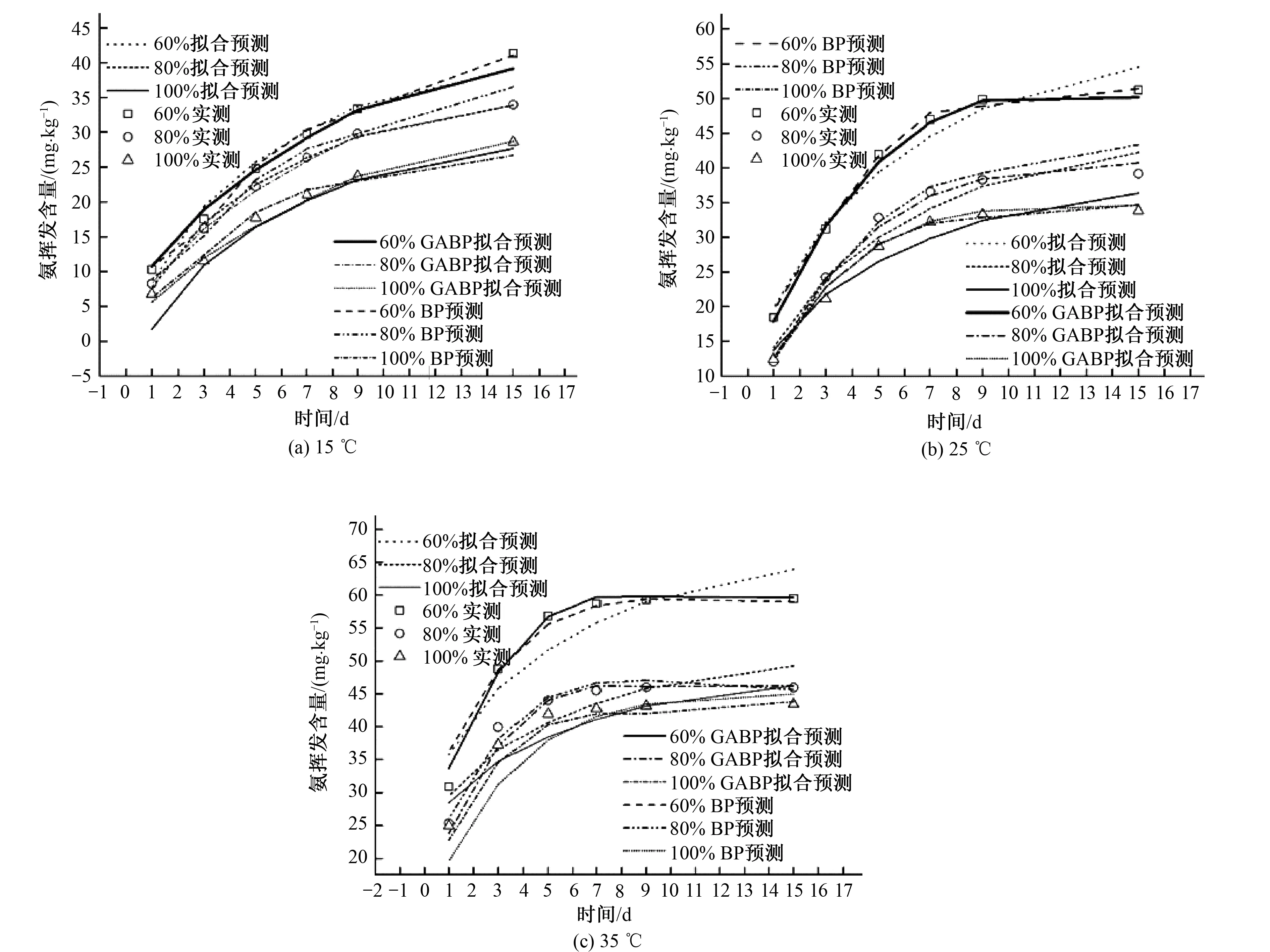
圖3為不同處理下土壤累積氨揮發逐日變化過程。由圖3可以看出,經不同水熱條件處理下的累積氨揮發具有相同的變化趨勢。在初始階段,氨揮發含量快速上升,然后隨著時間的推移逐漸趨于穩定,變化趨勢基本符合對數函數形式。在任意溫度下,不同含水量處理后的累積氨揮發含量大小均表現為:W60>W80>W100,表明氨揮發累積量與含水量之間呈現負相關關系。
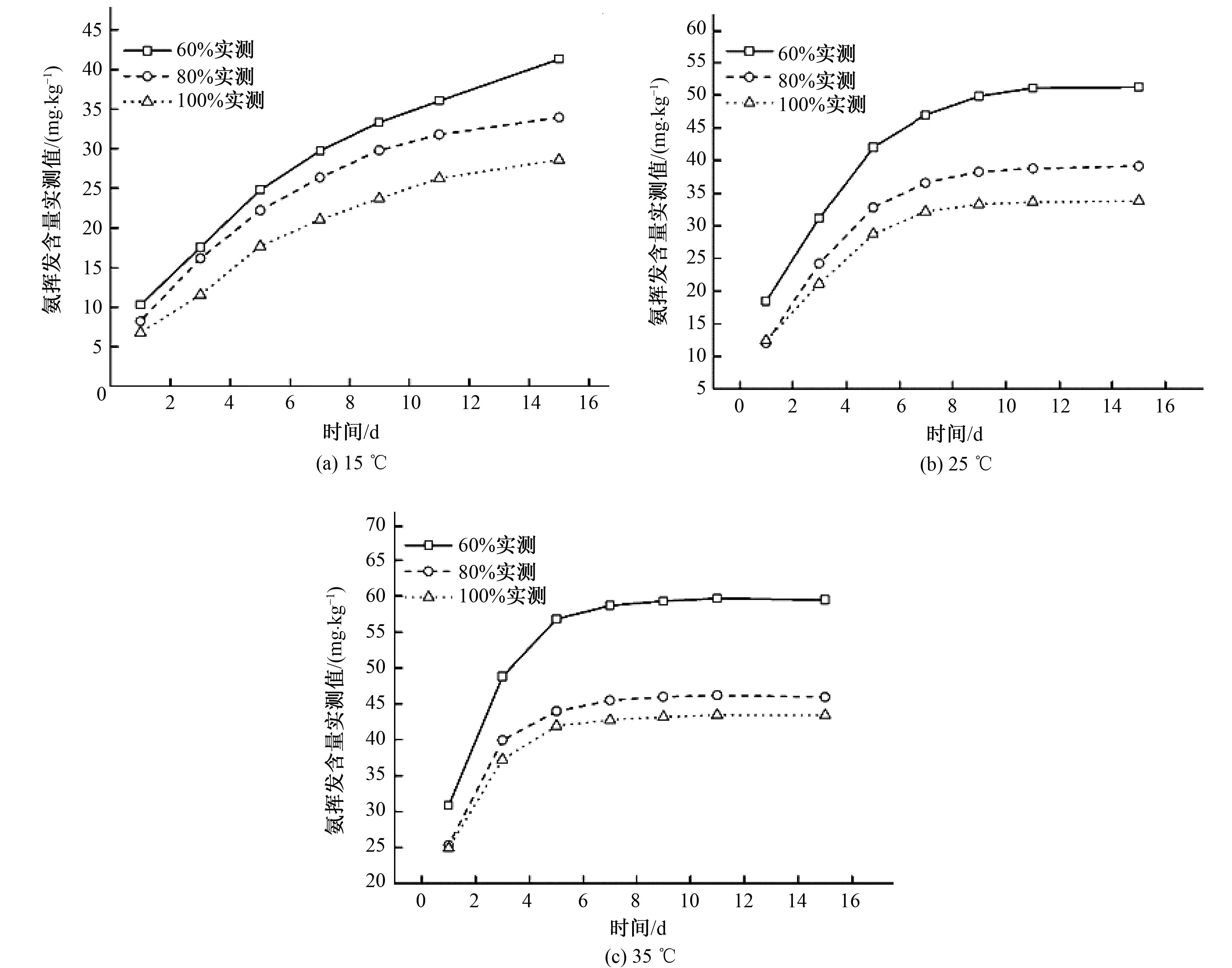
圖3 不同處理下土壤累積氨揮發量動態變化Fig.3 The cumulative ammonia volatilization content in soil under different treatments
由圖3還可以看出,不同溫度處理后的累積氨揮發含量大小表現為:35 ℃>25 ℃>15 ℃,表明土壤累積氨揮發量與溫度之間呈現顯著的正相關關系。此外,當溫度越高時,累積氨揮發量達到穩態的時間越早。
結合以上兩點,可以看出溫度對氨揮發累積量的正效應會受到含水量負效應的抑制,含水量對氨揮發累積量的負效應也會受到溫度正效應的抑制,說明溫度與含水量對累積氨揮發含量的影響存在交互作用,兩者表現為拮抗效應。
2.2 Elovich模型
圖4為不同水熱條件下土壤累積氨揮發Elovich模型模擬值與實測值的線性關系圖。表1為Elovich模型的具體參數及模擬精度。結合表1及圖4,可以看出,在訓練組中,模擬值與實測值的相關系數達到0.899~0.999,相關性方程的斜率為0.808 8~0.997 4,決定系數(R2)達到0.808 8~0.997 5,說明兩者之間具有良好的一致性。在15、25和35 ℃時,相對誤差分別為2.15%~6.45%,4.62%~6.63%和6.07%~6.78%,說明Elovich模型的模擬相對誤差較小。并利用SPSS軟件,采用配對t檢驗方法對模擬值與實測值的差異性進行了統計學分析,結果表明,在不同水熱條件下,|t|

表1 氨揮發Elovich模型參數及模擬精度表(t0.05(6)=2.447)(訓練組)Tab.1 The parameters and simulation accuracy of the Elovich model(training group)
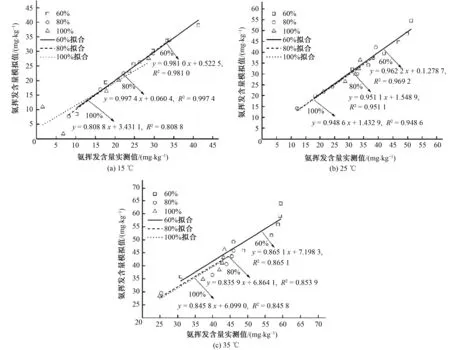
圖4 Elovich模型模擬值與實測值線性關系Fig.4 The linear relationship between the predictive value of Elovich model and observed value
首先將訓練樣本的54組數據帶入Elovich模型,從而確定出模型的具體參數和數學表達式。然后將檢驗樣本帶入該數學模型,得出檢驗集9組數據的氨揮發累積量的預測值。表2為檢驗土壤氨揮發量結果分析表。由表2可以看出,在檢驗樣本中,Elovich模型預測值與實測值的相對誤差介于7.35%~11.64%之間,平均相對誤差為9.57%。由此可見本文所建立的Elovich土壤氨揮發預測模型具有較高的精度,可以用于描述土壤氨揮發累積量的動態變化過程。
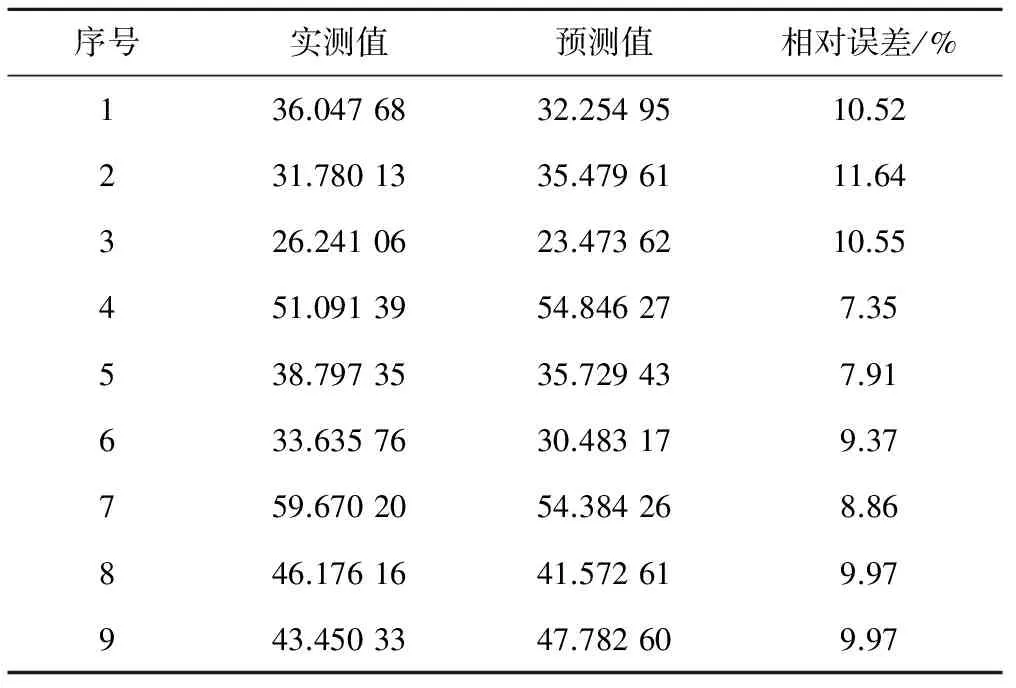
表2 氨揮發Elovich模型驗證結果精度表(檢驗集)Tab.2 The simulation accuracy of the verification resultof the Elovich model
圖5為不同處理下的Elovich模型參數的比較結果。參數K表征了土壤累積氨揮發速率。在任意含水量條件時,不同溫度處理后的參數K大小均表現為:35 ℃>25 ℃>15 ℃,即氨揮發累積速率與溫度呈現正相關關系。在15與25 ℃時,三種含水量處理后的參數K大小表現為:W100 圖5 Elovich模型參數Fig.5 The parameters of Elovich model 圖6為BP神經網絡模型的模擬值與實測值的線性關系。表3為BP預測模型的模擬精度表。結合圖6和表3可知,在訓練組中,模擬值和實測值之間的相關系數為0.998,決定系數(R2)達到0.995 5,說明模擬值與實測值之間具有良好的一致性。經計算,訓練組的平均相對誤差為2.76%,說明模擬相對誤差較小。利用SPSS軟件進行配對t檢驗,經計算,水熱耦合作用條件下,|t|值小于t檢驗臨界值,p值大于0.05,表明模擬結果與實測結果之間并無顯著統計學差異。 圖6 BP模型模擬值與實測值線性關系Fig.6 The linear relationship between the predictive value of BP model and observed value 在檢驗集中,預測值和實測值的相關系數為0.926,決定系數(R2)為0.842 1,表明BP神經網絡的訓練結果較好,一致性較好。經計算可知實測值與預測值的平均相對誤差為8.23%,并通過SPSS軟件對結果進行配對t檢驗,|t| 表3 氨揮發BP預測模型精度表(t0.05(49)=2.010,t0.05(12)=2.179)Tab.3 The prediction accuracy of the BP model 圖7為GABP神經網絡模型的模擬值與實測值的線性關系。表4為GABP預測模型的模擬精度表。在訓練組中,模擬值與實測值之間呈線性相關,相關系數達到0.998,兩者之間的決定系數(R2)達到0.996 7。模擬值與實測值之間存在著一定的誤差,平均相對誤差為2.23%,并對兩者進行配對t檢驗,經計算,|t| 在檢驗集中,預測值與實測值的相關系數為0.983,說明兩者有較好的一致性。決定系數(R2)與平均相對誤差分別達到0.966 0和4.14%,進行配對t檢驗后,|t|值小于t檢驗臨界值,表明預測值與實測值之間無統計學差異。由此說明GABP模型具有較高的精度,采用該模型進行土壤累積氨揮發預測是合理可行的。 圖7 GABP預測模型模擬值與實測值線性關系Fig.7 The linear relationship between the predictive value of GABP model and observed value rMAPE/%R2t值自由度Sig訓練0.9982.230.99671.947490.057預測0.9834.140.96600.363120.723 圖8為3種土壤氨揮發累積量預測模型模擬結果對比圖。在15 ℃時,含水量為60%田持時,3種模型的模擬結果基本在實際值附近,其中GABP模型的模擬結果與實測值擬合效果最好;80%田持時,前端和中端部分3種模型結果接近,末端GABP模型模擬值高出實測值,而其他兩種模型較接近;100%田持時,Elovich模型的擬合效果不穩定,離實測結果有較大差距,而GABP模型的模擬結果基本與實測結果吻合,擬合效果較好[圖8(a)]。在25 ℃時,含水量為60%田持時,GABP模型的模擬效果與實測值基本吻合,Elovich模型的效果次之;而當含水量為80%,100%田持時,模擬效果依次為GABP模型>BP神經網絡模型>Elovich模型[圖8(b)]。在35 ℃時,3種不同含水量條件下,3種模型模擬效果基本接近,GABP模擬效果最為穩定,BP神經網絡模型次之[圖8(c)]。此外,結合表1、表3和表4還可以看出,Elovich、BP和GABP 3個模型的模擬值與實測值之間的決定系數和平均相對誤差的大小關系為:GABP>BP>Elovich。說明在水熱耦合作用下,GABP模型的模擬效果最接近實測值,擬合效果最好,具有較高的擬合精度,BP神經網絡次之,Elovich模型較其他兩種來說較差。 表5為3種不同預測模型的預測結果比較。由表5可以看出,在檢驗集中,BP、GABP和Elovich模型的平均相對誤差分別介于5.33%~8.51%、3.21%~5.32%和7.35%~11.64%之間,平均相對誤差分別為7.10%、4.05%和9.05%,說明GABP模型的預測誤差最小。綜上所述,3種模型的均具有較高的預測精度,為土壤氨揮發預測提供了一種高效準確的定量研究方法。相對而言,3種模型的預測效果好壞表現為:Elovich模型>BP模型>GABP模型。 圖8 不同模型的模擬值與實測值比較Fig.8 The comparison of the simulated values of different models and observed values 序號實測值Elovich模型預測結果相對誤差/%BP模型預測結果相對誤差/%GABP模型預測結果相對誤差/%136.0476832.2549510.5233.254957.7537.284634.13231.7801335.4796111.6429.479617.2432.684253.51326.2410623.4736210.5528.473628.5125.453825.32451.0913954.846277.3553.846275.3953.384154.13538.7973535.729437.9136.729435.3337.529743.52633.6357630.483179.3736.483178.4732.483973.21759.6702054.384268.8664.384267.9061.284364.56846.1761641.572619.9743.572615.6444.698233.24943.4503347.782609.9746.782607.6744.691574.84 基于水熱耦合作用下土壤氨揮發累積量的室內試驗,建立了Elovich、BP、GABP三種不同的預測模型,通過數學方法對土壤氨揮發累積量進行預測,接著對預測結果進行驗證,選取指標對模擬效果進行比較,并進行誤差分析。結果表明:三種模型基本都能滿足氨揮發動態變化過程的預測精度要求。三種模型的預測效果好壞表現為:GABP>BP>Elovich。GABP模型的預測結果相對誤差最小,相關系數和決定系數明顯優于其他兩種模型,具有更好的非線性擬合能力和更高的預測精度。 □ [1] 李菊梅,李冬初,徐明崗,等. 紅壤雙季稻田不同施肥下的氨揮發損失及其影響因素[J]. 生態環境學報, 2008,17(4):1 610-1 613. [2] WAH Asman,MA Sutton,JK Schjorring. Ammonia: emission, atmospheric transport and deposition[J]. New Phytologist, 1998,139(1):27-48. [3] A Fangmeier,A Hadwiger-Fangmeier,LVD Eerden,HJ J?ger. Effects of atmospheric ammonia on vegetation—A review[J]. Environmental Pollution, 1994,86(1):43-82. [4] KWVD Hoek.Estimating ammonia emission factors in Europe: Summary of the work of the UNECE ammonia expert panel[J]. Atmospheric Environment, 1998,32(3):315-316. [5] TaoW,Ukwuani A T. Coupling thermal stripping and acid absorption for ammonia recovery from dairy manure: Ammonia volatilization kinetics and effects of temperature,pH and dissolved solids content[J]. Chemical Engineering Journal, 2015,280:188-196. [6] 朱小紅,馬中文,馬友華,等.施肥對巢湖流域稻季氨揮發損失的影響[J].生態學報, 2012,32(7):2 119-2 126. [7] DM Miles,DE Rowe,TC Cathcart. High litter moisture content suppresses litter ammonia volatilization[J]. Poultry Science, 2011,90(7):1 397-405. [8] 董文旭,胡春勝,陳素英,等.保護性耕作對冬小麥一夏玉米農田氮肥氨揮發損失的影響[J]. 中國農業科學, 2013,46(11):2 278-2 284. [9] J Xu,S Peng,S Yang,W Wang. Ammonia volatilization losses from a rice paddy with different irrigation and nitrogen managements[J]. Agricultural Water Management, 2012,104(2):184-192. [10] 吳仕勇. 基于數值計算方法的BP神經網絡及遺傳算法的優化研究[D]. 昆明:云南師范大學, 2006.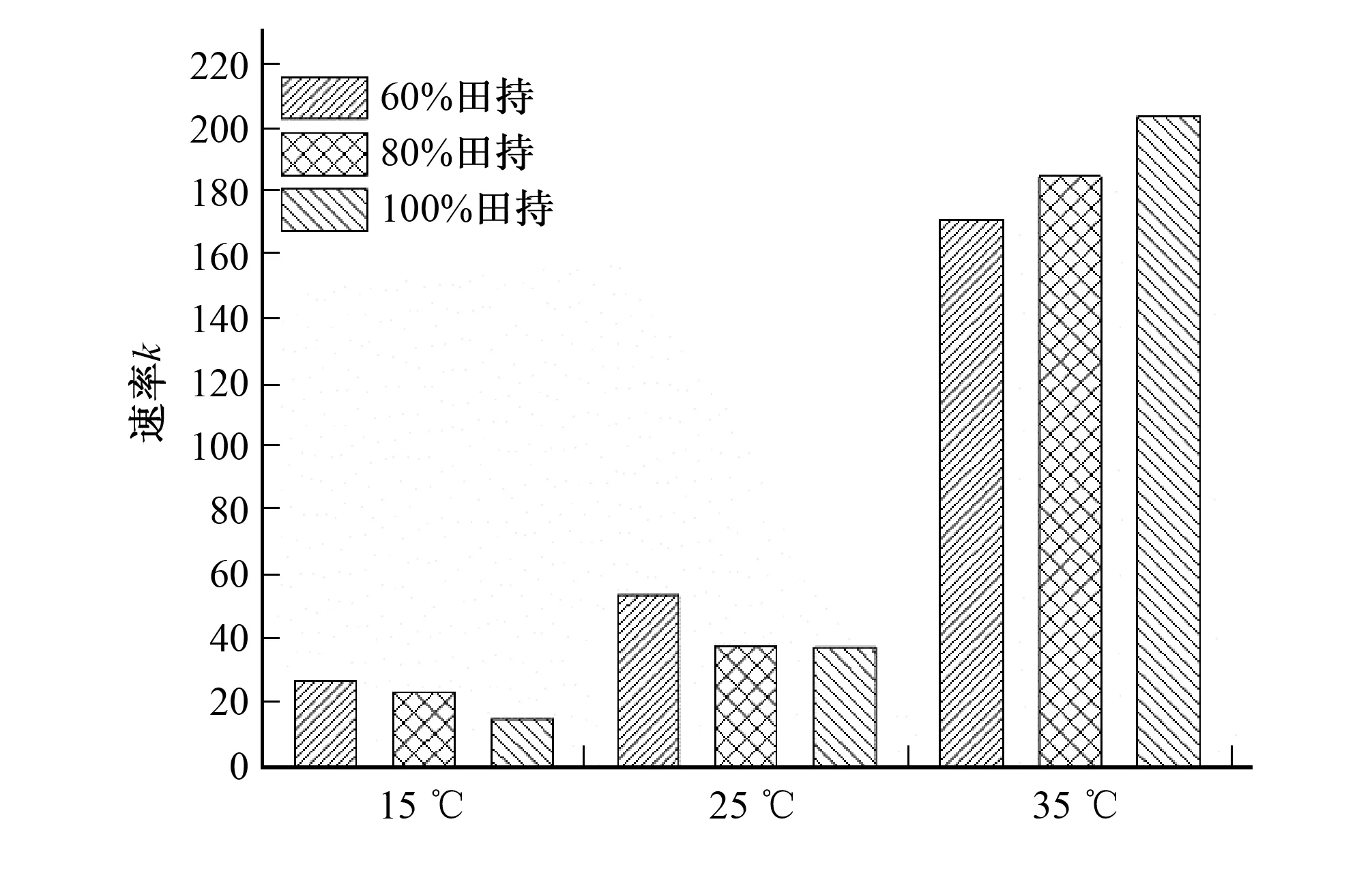
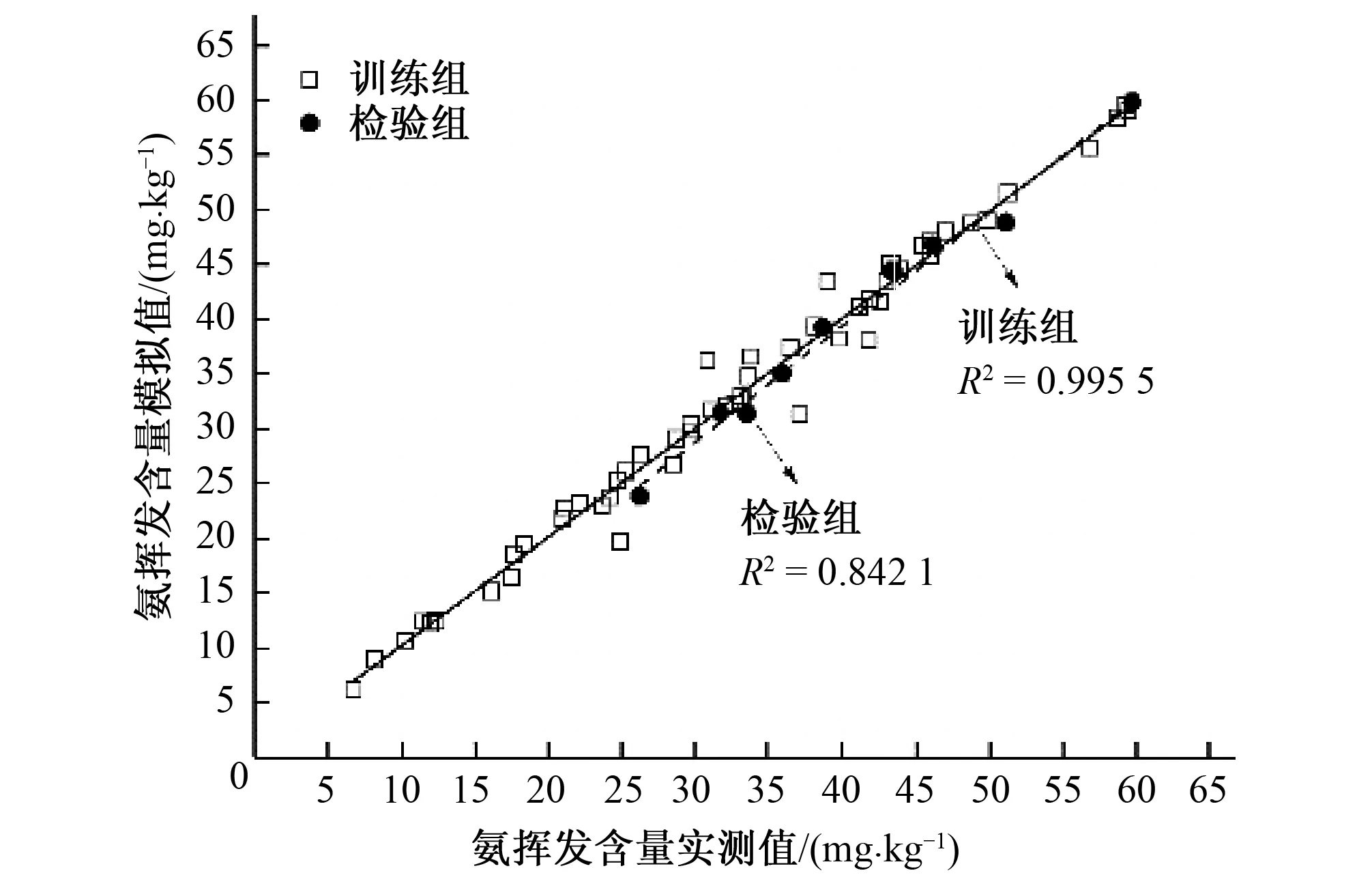
2.3 BP神經網絡模型

2.4 GABP模型


2.5 不同模型模擬效果比較
2.6 不同模型預測結果比較

3 結 論

