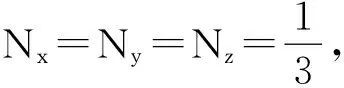均勻外電場中的一般橢球形導體

趙 強 籍萬新

(西安交通大學 1理學院；2數學與統計學院， 陜西 西安 710049)

教學經驗交流

均勻外電場中的一般橢球形導體

趙 強1籍萬新2

(西安交通大學1理學院；2數學與統計學院， 陜西 西安 710049)

根據一個均勻極化的一般橢球形電介質表面的極化電荷的分布規律與一個處在均勻外電場中具有相同形狀的導體橢球表面上感應電荷的分布規律的相似性，通過先求出均勻極化橢球表面上極化電荷的分布規律，然后用類比的方法給出了一個處在均勻外電場中具有相同形狀的一般橢球形導體表面上電荷的分布規律。

一般橢球； 面密度； 珀塞爾的觀點； 退極化因子

文獻[1]討論了均勻外電場E0中旋轉橢球形導體表面的感應電荷的分布規律，本文則討論均勻外電場E0中一般橢球形導體表面的感應電荷的分布規律。和文獻[1]一樣，本文也采用類比的方法，目的仍是為了避開拉普拉斯方程復雜的求解過程，用普通物理的方法解決問題，從而最大限度地突出問題中的物理圖像。

我們暫時拋開導體橢球問題不談，首先考慮一個與導體橢球形狀完全相同且沿主軸方向均勻極化的電介質橢球。設該電介質橢球面在直角坐標系中的方程為

(1)

若此電介質橢球的極化方向沿z軸的正方向，并且極化強度為P，則此電介質橢球表面的極化電荷密度為

(2)

式(2)中的n為電介質橢球表面的單位法向矢量，其具體表達式為

(3)

將式(3)代入式(2)中，有

(4)

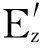
根據E.M.珀塞爾的觀點[2]，一個均勻極化的電介質橢球，其表面的極化電荷將在橢球的內部產生一個與極化方向完全相反的均勻的退極化場。在電介質橢球沿z主軸均勻極化的情況下，E.M.珀塞爾的觀點可以用如下的式子來表示

(5)

式(5)中的Nz可稱為電介質橢球的z主軸的退極化因子。在式(5)中將P除以ε0是處于量綱上的考慮，這樣可使Nz為一無量綱的純數，其數值完全由橢球的形狀來決定。將式(5)代入式(4)，有

(6)

根據對稱性，若電介質橢球的極化方向分別沿x主軸和y主軸時，極化電荷的面密度與退極化場之間的關系分別為

其中Nx、Ny分別是電介質橢球x主軸和y主軸的退極化因子，同樣是由橢球的幾何形狀決定的無量綱純數。

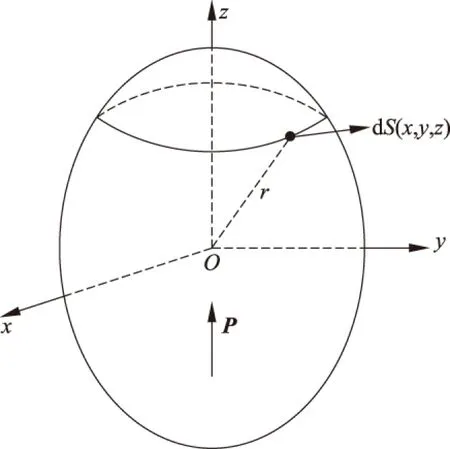
圖1 沿z主軸均勻極化的電介質橢球

下面求出式(6)～式(8)中的3個主軸的退極化因子Nz、Nx、Ny的具體表達式。如圖1所示，電介質橢球沿z主軸方向均勻極化，極化強度為P。在橢球表面任意一點(x,y,z)處選一小面元dS，面元dS上的極化電荷dq′在橢球中心O處產生的元場強在z軸上的分量為

橢球表面上所有的極化電荷在橢球中心產生的場強在z軸上的分量為(根據E.M.珀塞爾的觀點，此場強也是橢球內任意一點的退極化場的場強)

(9)

若用式(9)給出Nz的具體表達式，需將式(9)中的直角坐標作橢球坐標變換，即

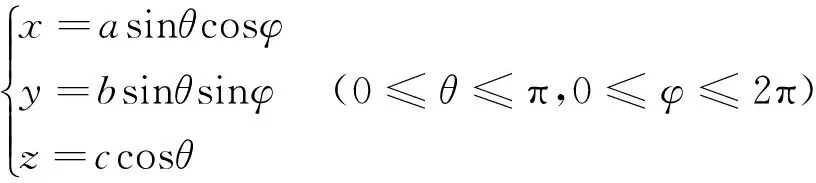
(10)

根據微分幾何的知識，橢球面法線的方向數為

橢球的表面積微元為

(11)

式(2)在橢球坐標下的形式為

(12)

將式(10)～(12)代入式(9)，有

(13)

比較式(13)和式(5)，有

(14)

式(14)就是電介質橢球的z主軸的退極化因子。從式(14)可以看出Nz完全由橢球的幾何形狀確定，即由橢球的3個主軸的半長度a、b、c確定的一個無量綱純數。

同樣的道理，可求出Nx和Ny的具體表達式為

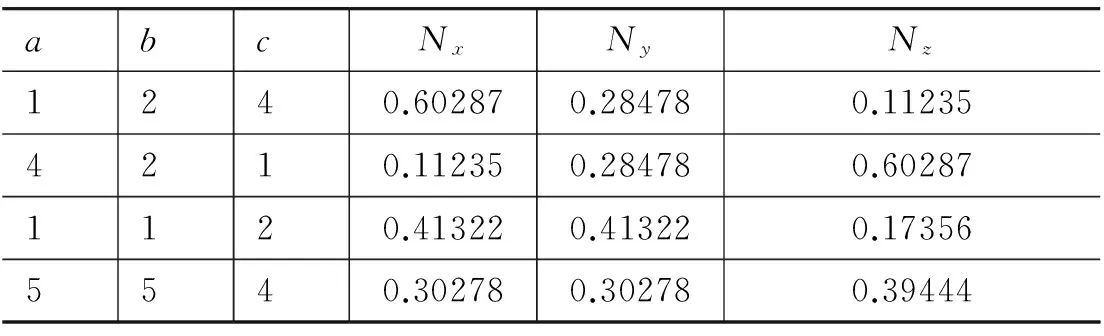
實際計算表明：0

Nx+Ny+Nz=1

(17)

若a≠b≠c，式(14)～式(16)無法給出關于a、b、c的解析表達式。但是由于有了計算機這一強大武器，Nx、Ny、Nz是否可表示為解析形式并不重要。只要將a、b、c的具體數值代入式(14)～式(16)中，用計算機可以很容易地求出任意精確度的數值。為了給大家一個直觀印象，筆者將4組a、b、c為特定值時所對應的Nx、Ny、Nz的值列于表1，供讀者參考[3]。

表1 退極化因子和橢球形狀之間的關系

至此，分別沿3個主軸方向均勻極化的電介質橢球表面的極化電荷的面密度與其退極化場之間的關系已完全研究清楚。現在討論處在均勻外電場E0中的與電介質橢球形狀完全相同的導體橢球問題。根據導體的靜電平衡條件，當導體橢球放到均勻外電場中時，導體表面的感應電荷將在導體內部產生一個與E0完全相反的均勻電場E(E=-E0)將E0抵消掉。當導體橢球內的感應電場E正好和同形狀的均勻極化橢球內的退極化場E′相等時，根據靜電場的唯一性定理，導體橢球表面的感應電荷的分布規律和同形狀的電介質橢球表面的極化電荷的分布規律完全一樣，也應有式(6)～式(8)的形式。因此，當外電場E0分別沿導體橢球的x主軸、y主軸及z主軸時，導體橢球表面上感應電荷的面密度分別為

式(18)～式(20)中的Nx、Ny、Nz的具體表達式仍由式(15)、(16)、(14)給出。

最后，若將導體橢球以任意姿式放進外電場E0中，這時E0與導體橢球的三個主軸的夾角分別為α、β、γ。在這種情況下，我們可將E0沿導體橢球的三個主軸進行分解，根據靜電場的疊加原理和靜電場的唯一性定理，最后的結果為

σ=σxcosα+σycosβ+σzcosγ

(21)

式(21)中的σx、σy、σz分別由式(18)～式(20)給出。

[1] 趙強，曲哲.均勻電場中的橢球形導體[J].物理與工程， 2016，26(1)：23-25. Zhao Qiang, Qu Zhe. Ellipsoidal conductor in uiform electric field[J]. Physics and Engineering, 2016, 26(1): 23-25. (in Chinese)

[2] 珀塞爾E.M..電磁學[M].伯克利物理教程.第2卷.南開大學物理系，譯.北京：科學出版社，1979：406.

[3] 朱旭,李換琴,籍萬新.MATLAB軟件與基礎數學實驗[M].西安：西安交通大學出版社,2008.

■

ELLIPSOIDAL CONDUCTOR IN UNIFORM ELECTRIC FIELD

Zhao Qiang1Ji Wanxin2

(1School of Science,2School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an Shaanxi 710049)

Based on the similarity between the distribution of induced charges on the surface of uniformly polarized dielectric ellipsoid and that on a conducting ellipsoid in external electric field with the same shape, we give the distribution of the charges on the surface of a conducting ellipsoid in external electric field through their analog, after achieving the distribution of induced charges on the surface of uniformly polarized ellipsoid with the same shape.

ellipsoid; surface density; Purcell; depolarization factor

2016-04-22

趙強，籍萬新. 均勻外電場中的一般橢球形導體[J]. 物理與工程，2017，27(1)：65-67.