一道高考試題的探究、推廣及探源*
安徽省歙縣中學(245200) 鄭觀寶
一道高考試題的探究、推廣及探源*
安徽省歙縣中學(245200) 鄭觀寶
問題(16高考四川卷理科第 20題)已知橢圓 E:直線l:y=-x+3與橢圓E有且只有一個公共點T.直線l′平行于OT,與橢圓E交于不同的兩點A、B,且與直線l交于點P.證明存在常數λ,使得|PT|2=λ|PA|·|PB|,并求λ的值.

一、一般化探究
解完本題后,我們自然會問,上述結論是否具有一般性?即:
問題1如圖1,已知橢圓E:直線l與橢圓E相切于點T(x0,y0),直線l′平行于OT,與橢圓E交于不同的兩點A、B,且與直線l交于點P,問是否存在常數λ,使得|PT|2=λ|PA|·|PB|成立?


至此,我們自然要問,上述平行割線PAB一定要與OT平行嗎?于是得到下列問題:
問題2 如圖2,橢圓 E:=1(a> b> 0),直線l與橢圓E相切于T(x0,y0).傾斜角為定角α的直線l′與橢圓E交于不同的兩點A、B,且與切線l交于點P.問是否存在常數λ,使得|PT|2=λ|PA||PB|成立?

圖2

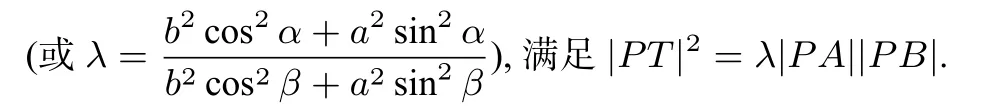
上述結論的形式與圓的切割線定理十分相似,這里暫且稱之為“橢圓的切割線定理”.
于是,我們得到
橢圓的切割線定理如圖2,直線l與橢圓E:1(a>b>0)相切于T(x0,y0),傾斜角為定角α的動直線l′與橢圓E交于不同的兩點A、B,且與切線l交于點P,則存在常數λ,使得|PT|2=λ|PA||PB|成立.
問題3上述定理中的常數能為1嗎?何時取到呢?

二、橢圓的割線定理
探究至此,并不完美.平面幾何中的圓還有割線定理,那么橢圓的也有割線定理嗎?
問題4 如圖3,設橢圓E:(a>b>0),傾斜角為定角α的動直線l1與橢圓E交于不同的兩點A、B,傾斜角為定角β的動直線l2與橢圓E交于不同的兩點C、D,與直線l1交于點P,問是否存在常數λ,使得|PA|·|PB|=λ|PC|·|PD|成立?
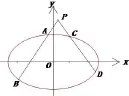
圖3


至此,我們證明了問題4的正確性,我們稱此結論為橢圓的割線定理.
(2)當橢圓退化為圓時即a2=b2時,始終有
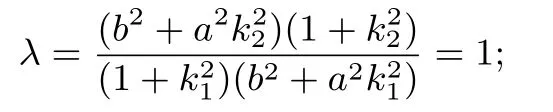
(3)當割線與橢圓的兩個交點C、D重合時,割線定理就變化為橢圓的切割線定理;
(4)當兩割線的交點P在橢圓內部時,就變化為“橢圓的相交弦定理”.
三、拋物線的切割線定理、割線定理和相交弦定理
定理設拋物線E:y2=2px(p/=0),傾斜角為定角α的動直線l1與拋物線E交于不同的兩點A、B,
(1)如圖4,設傾斜角為定角β的動直線l2與拋物線E相切于點T,與直線l1交于點P,則存在常數λ,使得|PT|2=λ|PA|·|PB|成立—拋物線的切割線定理.

圖4
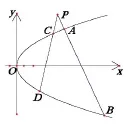
圖5
(2)如圖5,傾斜角為定角β的動直線l2與拋物線E交于不同的兩點C、D,與直線l1交于點P,則存在常數λ,使得|PA|·|PB|=|PC|·|PD|成立—拋物線的割線定理.


這樣,我們就證明了拋物線的切割線定理、割線定理、相交弦定理.
四、雙曲線的切割線定理、割線定理和相交弦定理
定理:設雙曲線E:,傾斜角為定角α的動直線l1與雙曲線E交于不同的兩點A、B,則
(1)設傾斜角為定角β的動直線l2與雙曲線E相切于點 T,與直線 l1交于點 P,則存在常數 λ,使得|PT|2=λ|PA|·|PB|成立.
(2)傾斜角為定角β的動直線l2與雙曲線E交于不同的兩點C、D,與直線l1交于點P(點P在),則存在常數λ,使得|PA|·|PB|=λ|PC|·|PD|成立.
此定理的證明過程與橢圓和拋物線的證明完全類似,限于篇幅,這里略去.結果如下:
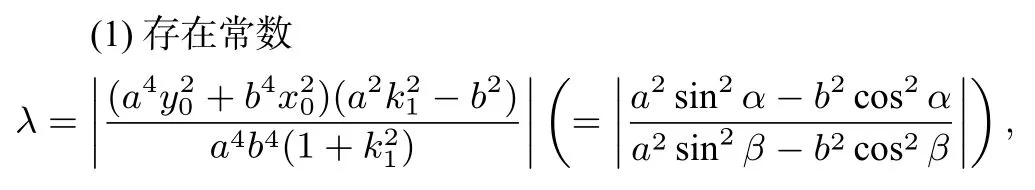

五、圓錐曲線的一條統一性質—圓冪定理
在圓中,相交弦定理、切割線定理、割線定理統稱為圓冪定理,那么,對上述的圓錐曲線三個定理能否統一表示呢?

于是得到:
圓錐曲線的統一性質(圓錐曲線的“圓冪定理”)設圓錐曲線E(標準方程),傾斜角為定角α的動直線l1與圓錐曲線E交于不同的兩點A、B,
(1)設傾斜角為定角β的動直線l2與圓錐曲線E相切于點T,與直線l1交于點P,則存在常數使得|PT|2=λ|PA|·|PB|成立;
(2)傾斜角為定角 β的動直線 l2與圓錐曲線 E交于不同的兩點C、D,與直線l1交于點P,則存在常數使得|PA|·|PB|=λ|PC|·|PD|成立.
綜上所述,文首所給的高考試題的真正“本源”就是上述圓錐曲線的“圓冪定理”,也可以說源自課本人教A版選修4—4第38頁例4及其推廣(參見文[1]).
[1]鄭觀寶.一道課本習題的探究、推廣與應用,數學教學,2011,1.
*本文系安徽省教育科學規劃重點課題(課題編號:JG12316)研究成果.

